精密坐标镗床进给系统热误差分析与预测

王新孟,杨军,梅雪松,雷默涵,赵亮,施虎

(西安交通大学机械制造系统工程国家重点实验室, 710049, 西安)



精密坐标镗床进给系统热误差分析与预测

王新孟,杨军,梅雪松,雷默涵,赵亮,施虎

(西安交通大学机械制造系统工程国家重点实验室, 710049, 西安)

为了预测数控机床运行时热误差对进给系统定位精度的影响,以精密坐标镗床为研究对象,采用红外热像仪和激光干涉仪分别测量进给系统在每个测点的丝杠温度和定位精度,提出进给系统热误差的最小二乘支持向量机(LS-SVM)预测方法,建立了关于温度与位置的预测模型。模型引入最小二乘支持向量机方法对机床进给系统热误差进行预测分析,较好地描述了进给轴热误差与温度、位置之间的非线性关系,且对样本的依赖度小,有很好的泛化能力,解决了目前线性拟合模型用特征平均温度替代当前测点温度进行计算而存在较大误差的问题。实验结果表明,与目前已经在数控机床上实际应用的线性预测模型相比,LS-SVM模型对进给系统热误差的预测精度可达90%,预测精度提高30%以上,取得了非常好的预测效果,具有较高的现实应用价值。

进给系统;热误差;热误差建模

目前,国产数控机床制造水平与国外相比还有一定差距。其中,国产精密坐标镗床虽然在一些关键性能指标上能接近或达到国外先进水平,但还存在一些国产机床普遍存在的问题,如稳定性差、可靠性低等。这些问题会随着机床使用时间的增加而变得更加突出,严重影响工件的加工质量。机床误差主要包括几何误差、热误差和切削力误差等[1]。大量研究表明,热误差约占机床总加工误差的70%[2],且所占比例随机床精密等级不同而有所差异,一般机床加工精度越高,热误差所占比例越大。机床加工过程中,电机、轴承、丝杠、刀具等会产生大量的热,热不平衡引起的机床机构变形、定位精度下降,严重影响加工精度,这种由热引起的误差称为热误差。机床热误差的影响因素很多,如热源强度及位置、机械结构、材料属性、机床加工环境及加工方式等,因此机床热误差具有非线性非稳态时变的特性。

研究机床热特性主要是分析机床进给系统和主轴系统的热特性,目前对主轴系统热误差预测模型的研究较多,提出了很多研究方法和热误差预测模型,且具有很高的预测精度,如时间序列预测模型、BP神经网络预测模型等。关于进给轴系统热误差研究却相对较少,热误差预测模型简单,主要因为进给系统热特性更复杂,实验中丝杠温度不易获取,实验成本更高等。文献[3]建立了滚珠丝杠热误差的多元回归模型。文献[4]通过与进给轴平衡安置的石英管求出进给轴的热膨胀量,间接建立了基于神经网络(ANN)的位置-热误差模型。文献[5]利用激光干涉仪对立式加工中心的进给系统热误差进行了研究,给出了较为完整的测试方法。文献[6]利用红外热像仪对滚珠丝杠的温度场进行了测量,并建立了进给轴热误差与关键测点温度的关系模型。文献[7]分析机床进给轴系统在不同工况条件下的温度场分布及热变形,取得了较为理想的预测结果。

本文以精密坐标镗床为研究对象,利用红外热像仪、激光干涉仪以及由本课题组自行研制的温度采集系统等对机床进给系统进行同步数据测量。分析了进给系统在不同进给速度下的温度分布,研究了坐标镗床在受热膨胀下定位精度的变化规律以及影响因素,对进给系统热误差特征进行了分析,提出进给系统热误差的最小二乘支持向量机(LS-SVM)预测方法,建立了关于温度与位置的预测模型。与目前广泛应用的模型相比,本文模型具有非常好的预测精度和通用性,而且支持向量机是基于统计学习和结构风险最小化原理的方法,对样本的依赖度小,有很好的泛化能力,具有非常好的现实应用价值。

1 实验设备及测量方法

1.1 实验对象及测试系统

本文研究对象为昆明机床厂研制的大型精密坐标镗床,如图1所示。镗床进给轴X、Y、Z均为线性同步双电机驱动,进给行程分别为1 200 mm、1 000 mm、1 000 mm,在20 ℃恒温车间内机床进给系统定位精度为3 μm,重复定位精度为1.5μm,理论最大进给速度F=64 m/min,实际加工最大进给速度F=45 m/min。

图1 精密坐标镗床

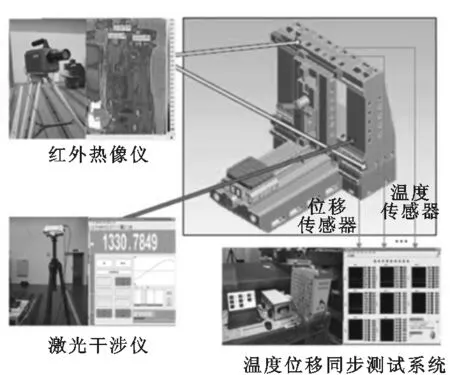
图2 进给系统热特性测试系统

测试系统包括一台雷尼绍公司XL80激光干涉仪,一台FLIR SC7000红外热像仪及一套温度位移同步测试系统,测试系统如图2所示。激光干涉仪用来测量机床进给系统的定位误差;激光干涉仪补偿器可以修正空气温度、湿度、压强等环境因素对测量精度的影响;红外热像仪可以在机床运行时采集丝杠的温度,并可以直观地了解热源对其分布的影响;温度位移同步测试系统中利用高精度电涡流传感器测量丝杠末端受热膨胀量,记为S1,传感器用磁性表座固定在丝杠末端;利用磁吸式热电阻温度传感器PT100测量温度,记为T1～T9。

1.2 测试方法[8-9]

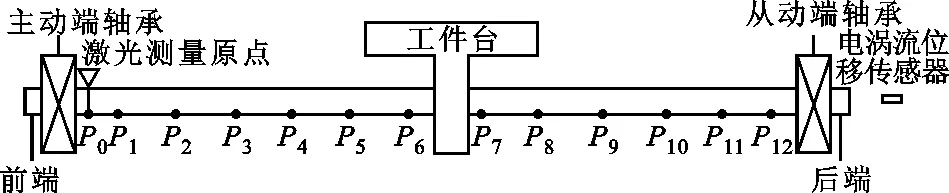
图3 轴上测点分布示意图

本实验是在20 ℃恒温实验室进行的,以X进给轴在不同进给速度下(6、12、18、24 m/min)测量丝杠关键点的温度、丝杠末端位移和X轴定位精度。进给轴在测量范围[50 mm,1 150 mm]内分为12个测点,如图3所示,相邻测点相距100 mm,定位误差的测量方法依据VDI/ISO标准,每次测量点停留5 s,每组数据测量3个往复,设置反向越程为2 mm,消除反向间隙。开机运行前先冷机测一组数据作为机床的几何误差,便于去除以后数据中的几何误差,得到热误差。每组定位误差数据测量间隙为30 min,测量时间为10 min,为了减少测量时产生的热量对测量结果的影响,测量时进给速率降为0.5 m/min。温度数据每5 min保存一次,温度测点及位移测点安装位置见图4,具体位置如下:①上端丝杠部分的电机外壳温度T1、前轴承温度T6、螺母温度T5、后轴承温度T7;②下端丝杠部分的电机外壳温度T4、前轴承温度T9、螺母温度T2、后轴承温度T8;③环境温度T3;④X轴下端丝杠末端热伸长量S1。测点冷态时的几何误差为

(1)

测点热误差为

(2)

丝杠特征平均温度为

(3)

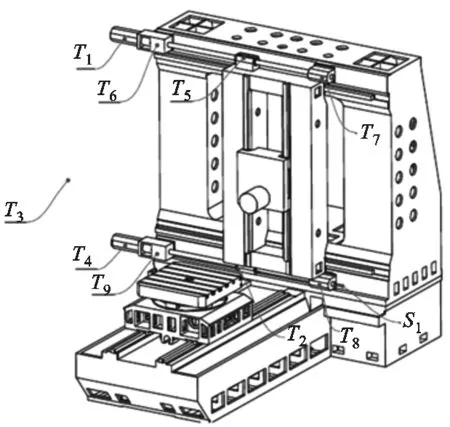
图4 温度、位移传感器安装位置示意图

式中:i为温度测点编号,i=1,2,…,12;j为测量数据的组数编号,j=1,2,…,N,机床在580 min时已经达到热平衡,对应N=14。

2 实验结果及分析

机床产生的热误差是由于机床受热膨胀、结构热不平衡引起的,热误差肯定与温度有关。由进给轴丝杠受热膨胀不均以及定位光栅尺的热变形引起的机床的定位误差,在不同的坐标位置也应该是不一样的,本次实验数据也验证了这一点。图5可以直观了解加工过程中机床温度及热源分布情况,温度越高的地方红外辐射能量越大,在图中就显示的越白亮,经过处理可以获得需要部位的温度值,通过这种方法获得丝杠上测点的温度值。

图5 红外热像仪图谱

2.1 机床温度场分析

温度位移同步测试系统测得机床进给系统热敏感点温度,如图6所示。由图可知,环境温度大约稳定在20 ℃,X进给轴上电机温度最高,为39.26 ℃,次高点是进给轴下电机,为35.3 ℃。本研究对象精密坐标镗床进给系统为双驱结构,电机为进给系统动力源,其产生的热量应该是最大的,为最主要热源,PT100温度传感器磁吸在电机外壳上,电机内部温度应该高于测量值。双驱结构在同步控制和结构、制造上的差异,导致上、下电机温度不同,观察其他数据可得,上部温度测量值都高于对应的下部温度测量值。距离上电机最近的上轴承温度约为30.9 ℃,仅低于上下电机温度,因为电机产生热量首先通过靠近的轴承向外传导,其次轴承在运行过程中也会产生大量的热。由于丝杠后端的轴承远离主要热源,温度相对较低,只有25.7 ℃。图6中数据有明显的周期波动,因为每隔30 min就要降低进给速度测量点的定位精度,测量期间产生的热量减少,温度下降,图中的波动周期也刚好对应这个时间段。通过式(3)计算丝杠的特征平均温度,得出在不同进给速度下丝杠特征平均温度随时间的变化见图7,发现进给速度越大,丝杠温度越高。

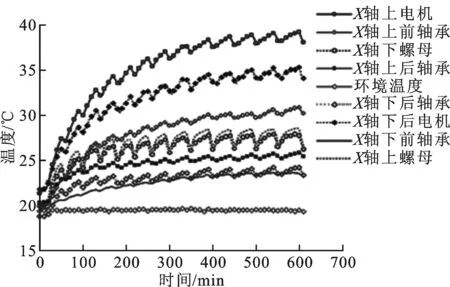
图6 温度敏感点温度值

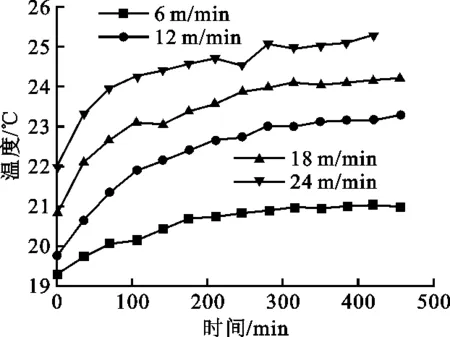
图7 不同进给速度下丝杠平均温度

2.2 机床热误差分析

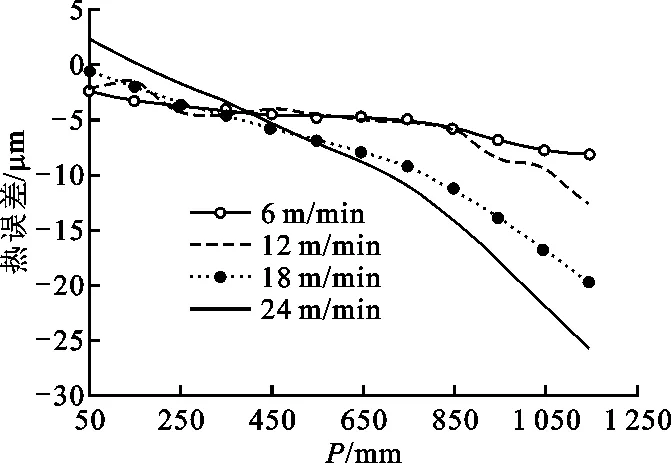
图8 不同进给速度下稳态定位误差

图8是机床在达到热平衡后,不同进给速度下不同测点上的机床热误差随坐标变化曲线图。由图可知,机床达到热平衡后热误差在靠近电机端为正值,远离电机端为负值,且远端误差绝对值较大,中间各点误差随坐标近似线性分布。当进给速度越大,温度越高,则热膨胀引起的热误差就越大,图8中数据也验证这个规律。以测点1 150mm处为例,进给速度为6、24m/min时,热误差达到最小值和最大值,分别为-8.2、-25.8μm。由图9可知,机床运行时间越长,平均温度越大,则定位误差越大。从图10可明显看出,误差随着测点坐标增加而增大,在520min时,丝杠特征平均温度为24.2 ℃,测点的整体热误差最大,此时在测点1 150mm处,热误差最大约为-16.8μm。

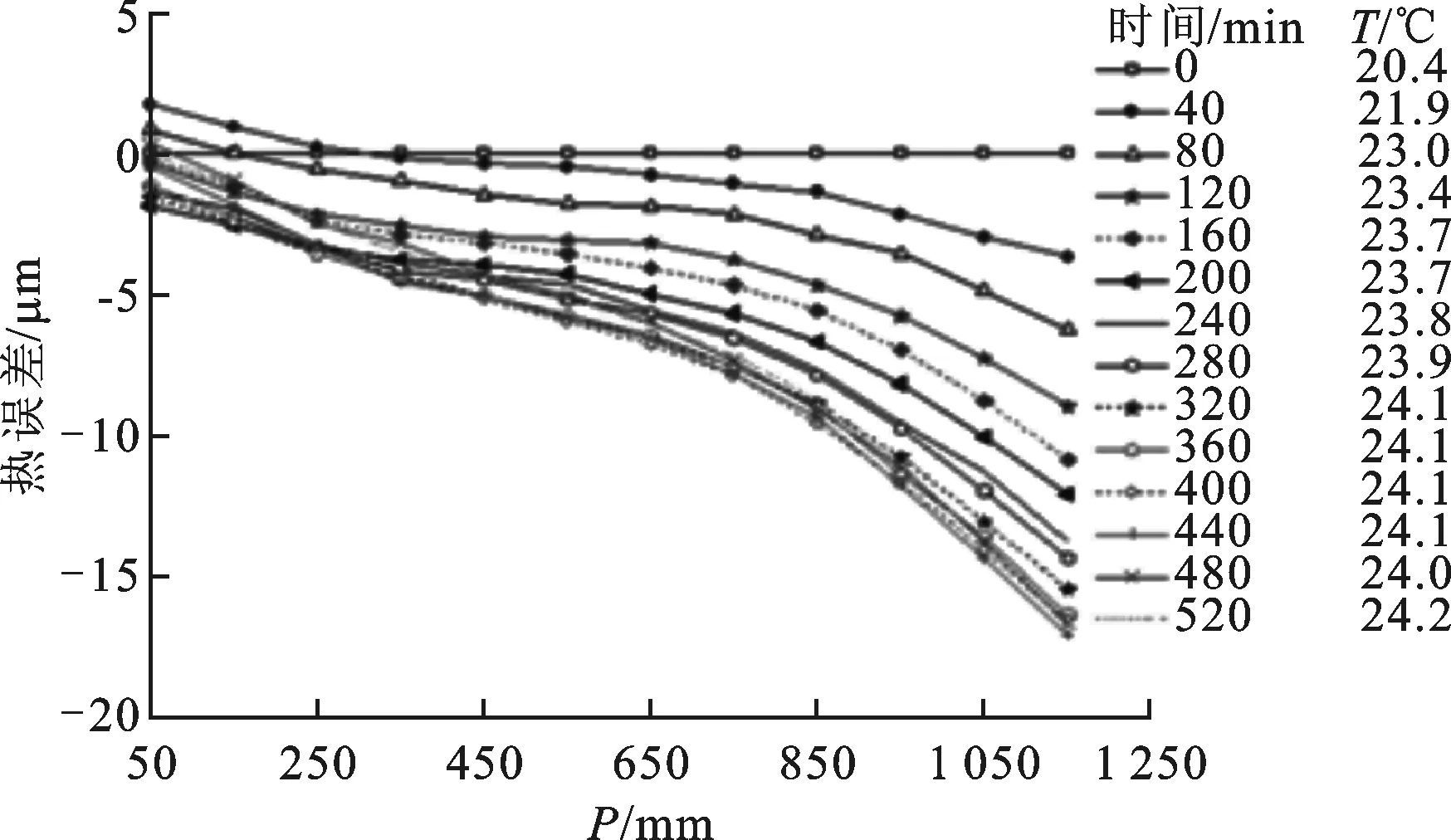
图9 F=18 m/min时进给轴误差与位置和温度关系

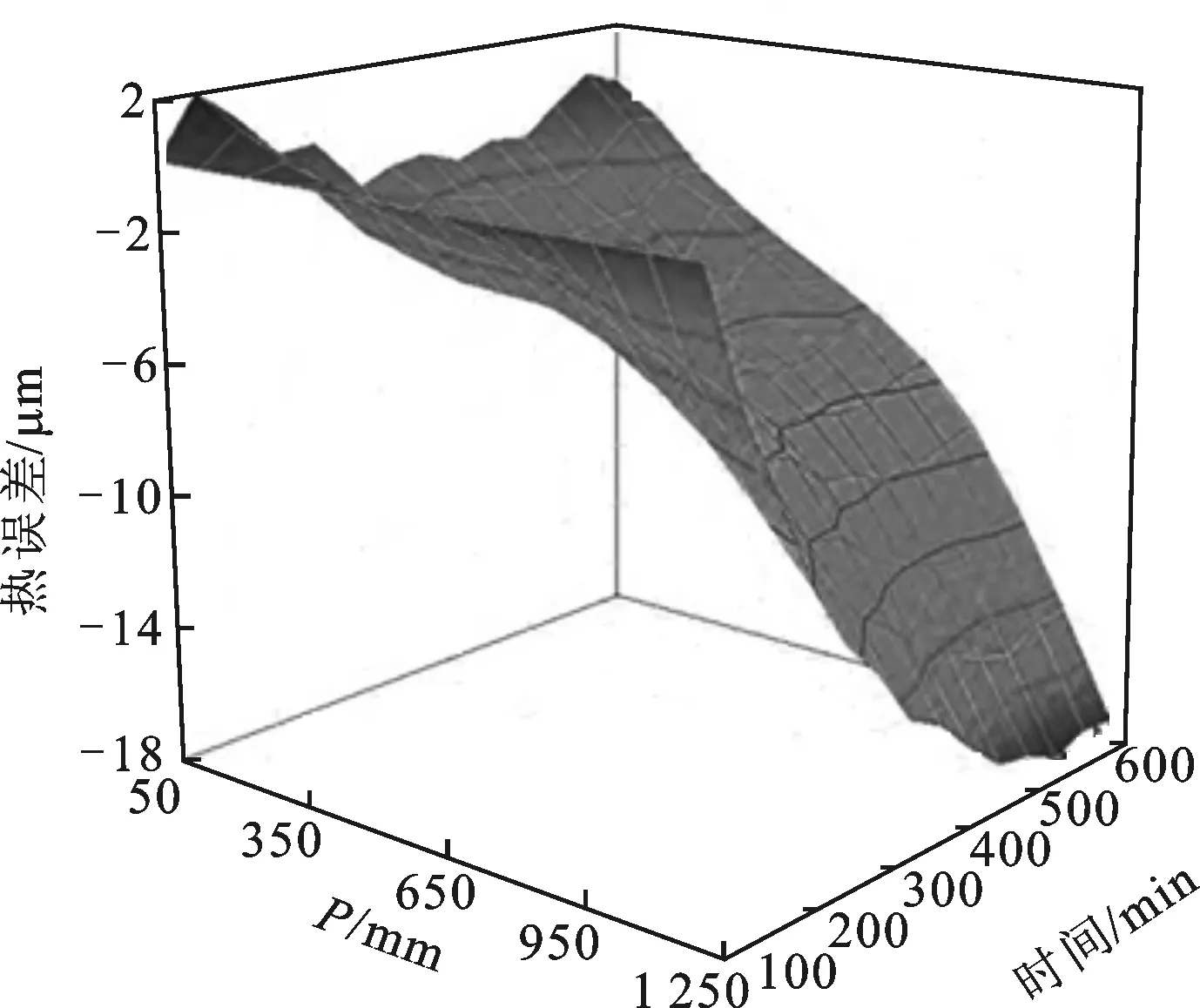
图10 F=18 m/min时进给轴误差与位置和时间关系

3 进给轴热误差建模

清楚了热误差的影响因素之后,需要对机床热误差进行建模预测。目前,进给轴系统热误差预测模型多为线性拟合模型,并且已经在许多工业机床数控系统中得到应用,如西门子828D、840D数控系统及国产华中数控系统等,并取得一定的效果,但是该模型简单,预测精度较低[10-11]。本文以精密坐标镗床的X轴为研究对象,选取进给速度F=18m/min,对进给系统热误差进行建模分析。

3.1 最小二乘支持向量机

支持向量机本质是一个二类分类的优化策略,使分类之间距离最大化。对于非线性分类问题,通过选取适当的核函数K(x,xi)把数据映射到高维空间,则可以将任意的数据映射为线性可分,具有非常好的非线性处理能力。文献[13]在标准SVM的目标函数中增加了误差平方和项,利用误差平方和作为损失函数,提出了最小二乘支持向量机方法,并采用加权的方法成功地解决了模型鲁棒性弱以及稀疏矩性不足的缺陷。本支持向量机模型基于结构风险化监督学习策略,目标函数为

(4)

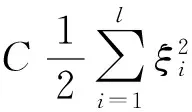
构建拉格朗日函数

(5)

式中:λi(i=1,…,l)是拉格朗日乘子。根据极值存在条件,拉格朗日函数对各变量的偏导数满足

(6)

得到

(7)

式中:K(xi,xj)是核函数。为满足Mercer条件的任意对称函数,选用径向基函数作为核函数

(8)

由式(6)求得λi、b,参数C和核函数参数σ通过交叉辨识(CV)的方法求得。

3.2 最小二乘支持向量机建模

LS-SVM回归模型解析式为

(9)

模型输入为x(P,T),P是测点在丝杠上的位置坐标,T是当前测点对应的丝杠位置上的温度;输出为对应位置、温度下的热误差。由于热误差影响因素关系比较复杂,为提高模型预测精度,可以增加模型的输入量,分别增加(PT)1/2和(P2+T2)1/2,此时预测模型输入量变为x(P,T,(PT)1/2,(P2+T2)1/2),计算得模型参数C、σ、b、l分别为18.5、0.084、0.568 6、89。

3.3 热误差预测模型比较

线性拟合模型[14-16]建模过程本文不再赘述。图11是温度为21.9 ℃和24.2 ℃时,两种模型热误差预测值随位置变化曲线。从图中可见:线性拟合模型预测最大误差绝对值在对应温度下分别是1.6 μm和4.43 μm,误差绝对平均值为0.647 μm和2.31 μm,预测精度为51.8%和65.6%;LS-SVM模型预测最大误差绝对值分别是0.197 μm和0.725 μm,误差绝对平均值为0.074 μm和0.259 μm,预测精度高达94.5%和96.1%。图12和图13分别是250 mm和650 mm测点处的热误差随时间变化曲线。从图中可见:线性拟合模型预测精度分别为56.46%和60.8%;LS-SVM模型预测精度分别为91.68%和93.27%。最小二乘支持向量机模型预测精度明显高于线性拟合模型。

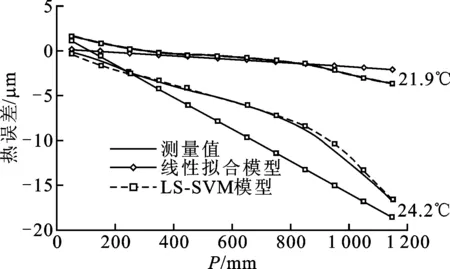
图11 不同特征平均温度下热误差预测值随位置变化图

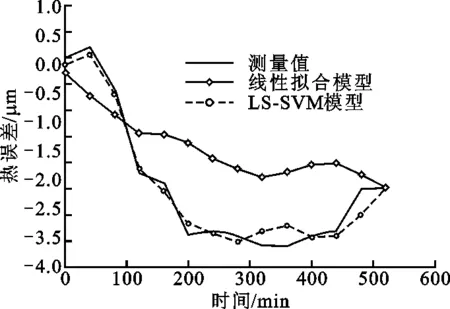
图12 250 mm测点处的热误差变化曲线图

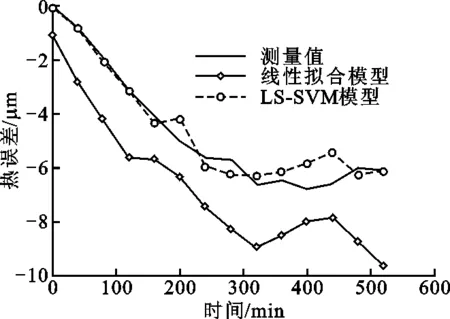
图13 650 mm测点处的热误差变化曲线图

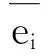
(10)

(11)

(12)

(13)

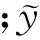
表1 误差预测模型优劣评价参数

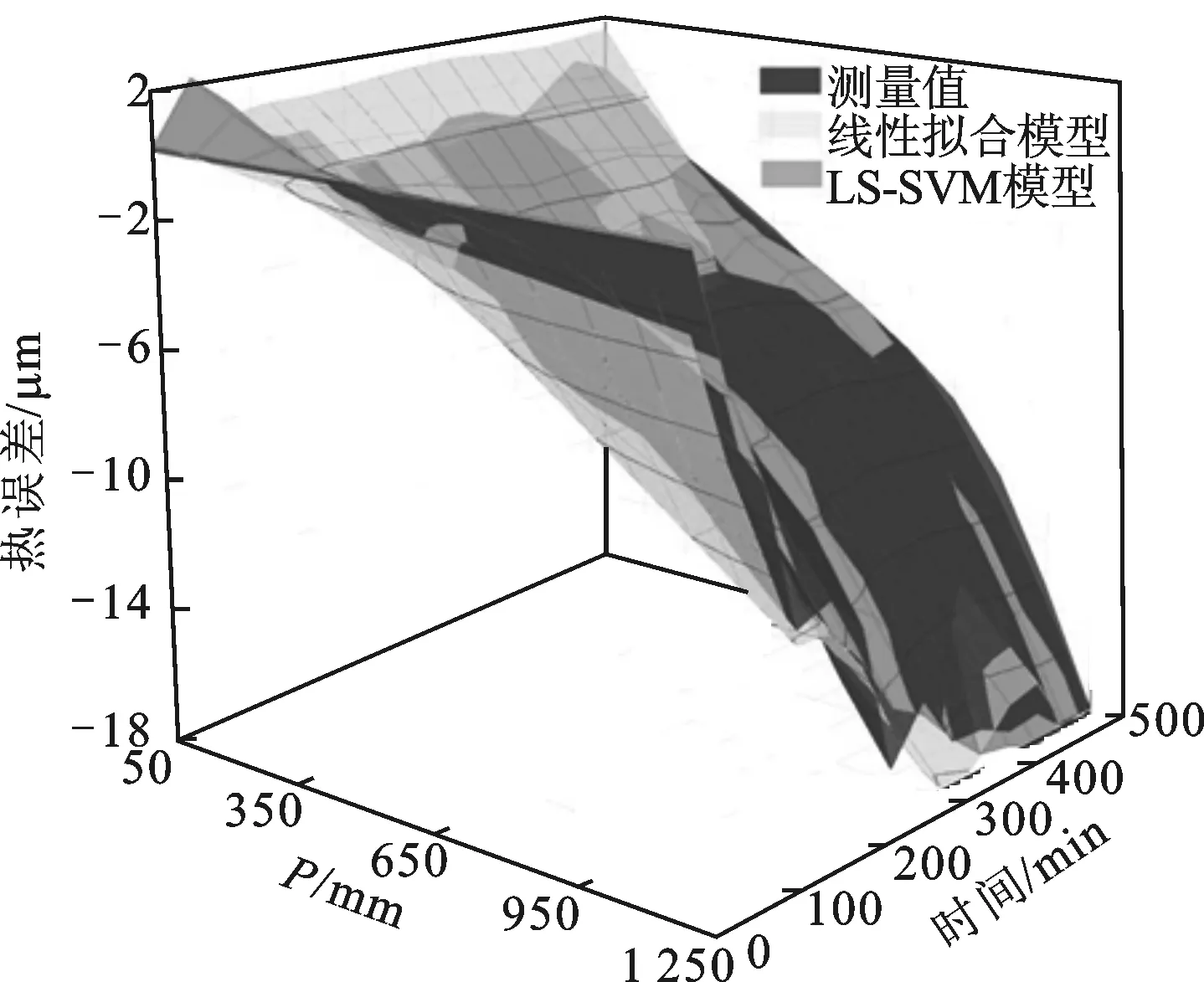
图14 线性拟合、LS-SVM模型误差预测图

4 结 论

本文测量了不同进给速度下进给系统在不同位置、温度下的热误差,分析了加工过程中机床产生的热量对进给轴系统定位精度的影响。以精密坐标镗床进给系统X轴为例,建立了LS-SVM热误差预测模型,验证了LS-SVM模型可以较好地描述进给轴热误差与温度、位置之间的非线性关系。同时,可以用相同方法建立进给系统其他轴以及主轴的预测模型,最后建立整机在不同温度和进给坐标下的热误差预测模型。

线性拟合模型在热误差计算过程中,把同一时刻下不同位置测点对应的温度统一用丝杠特征平均温度替代,而每个测点的热误差是由当前位置和温度共同决定的,这种近似用特征平均温度替代当前测点的温度计算测点热误差,无论模型怎么完善都会存在较大的误差。支持向量机是基于统计学习和结构风险最小化原理的方法,对样本的依赖度小,有非常强的非线性问题处理能力。通过对比两种模型热误差预测精度,LS-SVM模型具有非常高的预测精度,有较好的应用价值。

[1] 杨建国, 范开国. 数控机床误差实时补偿技术 [M]. 北京: 机械工业出版社, 2013: 126-129.

[2] BRYAN J. International status of thermal error research (1990) [J]. CIRP Annals: Manufacturing Technology, 1990, 39(2): 645-656.

[3] HUANG S C. Analysis of a model to forecast thermal deformation of ball screw feed drive systems [J]. Int J of Mach Tools and Manufact, 1995, 35(8): 1099-1104.

[4] CHEN J S. Fast calibration and modeling of thermally-induced machine tool errors in real machining [J]. Int J Mach Tools Manufact, 1997, 35(2): 159-169.

[5] WU C H, KUNG Y T. Thermal analysis for the feed drive system of a CNC machine center [J]. Int J of Mach Tools and Manufact, 2003, 43(15): 1521-1528.

[6] HEISEL U, KOSCSAK G, STEHLE T. Thermography based investigation into thermally induced positioning errors of feed drives by example of a ball screw [J]. CIRP Annals: Manufacturing Technology, 2006, 55(1): 423-426.

[7] YANG J, ZHANG D H, MEI X S, et al. Thermal error simulation and compensation in a jig-boring machine equipped with a dual-drive servo feed system [J]. Proc IMechE: Part B J Engineering Manufacture, 2015, 229(51): 43-63.

[8] 杨军, 施虎, 梅雪松, 等. 双驱伺服进给系统热误差的试验测量与预测模型构建 [J]. 西安交通大学学报, 2013, 47(11): 53-59. YANG Jun, SHI Hu, MEI Xuesong, et al. Measurement and modeling of thermal errors in dual-drive servo feed system [J]. Journal of Xi’an Jiaotong University, 2013, 47(11): 53-59.

[9] 杨军, 梅雪松, 赵亮, 等. 基于模糊聚类测点优化与向量机的坐标镗床热误差建模 [J]. 上海交通大学学报, 2014, 48(8): 1175-1182. YANG Jun, MEI Xuesong, ZHAO Liang, et al. Thermal error modeling of a coordinate boring machine based on fuzzy clustering and SVM [J]. Journal of Shanghai Jiaotong University, 2014, 48(8): 1175-1182.

[10]李永祥, 杨建国. 数控机床热误差的混合预测模型及应用 [D]. 上海: 上海交通大学, 2006.

[11]沈金华, 李永祥, 杨建国, 等. 数控车床几何和热误差综合实施补偿方法应用 [J]. 四川大学学报, 2008, 40(1): 163-166. SHEN Jinhua, LI Yongxiang, YANG Jianguo, et al. A real-time compensation method for the geometric and thermal error on CNC turning machine [J]. Journal of Sichuan University, 2008, 40(1): 163-166.

[12]VAPNIK V N. Statistical learning theory [M]. New York, USA: Wiley, 1998: 375-567.

[13]SUYKENS J A K, DE B J, LUKAS L, et al. Weighted least squares support vector machines: robustness and sparse approximation [J].Neurocomputing, 2002, 48(1): 85-105.

[14]陈颖, 杨楠. 应用回归分析 [M]. 上海: 复旦大学出版社, 2008: 44-92.

[15]GALIMBERTI G, SOFFRITTI G. A multivariate linear regression analysis using finite mixtures of t distributions [J]. Computational Statistics and Data Analysis, 2014, 71: 138-150.

[16]李志林, 尹建华. Matlab软件在建立回归模型中的应用 [J]. 数理统计与管理, 2005, 24(S1): 452-456. LI Zhilin, YI Jianhua. The application of MATLAB to structure regression model [J]. Journal of Applied Statistics and Management, 2005, 24(S1): 452-456.

(编辑 杜秀杰)

Analysis and Prediction for Thermal Error of Precision Coordinate Boring Machine

WANG Xinmeng,YANG Jun,MEI Xuesong,LEI Mohan,ZHAO Liang,SHI Hu

(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

To predict the effect of heat deviation on positioning accuracy of feed system in a running CNC machine, for a precision coordinate boring machine, the temperature accuracy in every measuring point of the system is measured by infrared thermal imager and the positioning accuracy is measured by laser interferometer simultaneously, then the least squares support vector machine (LS-SVM) prediction method of thermal error in feed system is adopted to establish a prediction model of temperature and location. LS-SVM prediction method is introduced into the prediction model to predict the thermal error in the feed system. The model well describes the nonlinear relationship between the thermal errors of position and temperature with slight dependence on samples and good generalization ability. The difficulty that the prediction error gets greater because the average characteristic temperature is considered instead of the current measuring point temperature in establishing linear prediction model is solved. The results show that the prediction precision of thermal error by LS-SVM model reaches 90%, 30% higher than that by the existing linear prediction model for NC machine.

feed system; thermal error; thermal error modeling

2015-04-22。

王新孟(1990—),男,硕士生;杨军(通信作者),男,讲师。

国家重点基础研究发展计划资助项目(2011CB706805);国家重大科技成果转化资助项目(2012HZ01)。

时间:2015-08-18

10.7652/xjtuxb201510004

TH161;TG532

A

0253-987X(2015)10-0022-07

网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150818.0924.004.html