非均质复合材料力学性能的确定性多尺度计算方法

裴世源,徐华,2

(1.西安交通大学现代设计与转子轴承系统教育部重点实验室, 710049, 西安;2.新疆大学机械工程学院, 830046, 乌鲁木齐)



非均质复合材料力学性能的确定性多尺度计算方法

裴世源1,徐华1,2

(1.西安交通大学现代设计与转子轴承系统教育部重点实验室, 710049, 西安;2.新疆大学机械工程学院, 830046, 乌鲁木齐)

针对具有多尺度特性的非均质复合材料进行结构强度分析,提出了一种确定性多尺度计算方法——有限细胞法(FCM)。该方法通过矩阵凝聚和插值近似得到粗网格的刚度矩阵,在计算得到粗网格解后,通过回代技术可获得全域细网格解。为验证FCM的计算精度和计算效率,构造了多个数值算例,并与理论和有限元(FEM)结果进行了对比,结果发现:相对于FEM,FCM可显著扩大计算规模,提高计算速度,且易于并行;相对于其他多尺度计算方法,FCM在构造粗网格刚度矩阵过程中无需引入微观边界条件,计算精度高,易于降尺度计算。因此,FCM是分析复合材料结构强度的一种有效的多尺度算法,同时该方法易于推广至多尺度的非线性结构分析、热分析、地下水渗流分析等领域。

有限细胞法;多尺度计算;非均质复合材料

自然界和工程应用中的很多材料都具有多尺度特征,准确描述这些材料的整体细观力学行为是当今科学界和工程界所面临的挑战之一。传统数值方法在求解这些问题时需耗费大量的计算资源,虽然超级计算机和并行计算的出现在一定程度上缓解了计算难度,但对于很多大规模多尺度问题仍难以求解。在保证计算精度的前提下,发展高效的多尺度计算方法是当今计算力学领域的研究热点[1-2]。

近些年来,国内外学者已提出了各种多尺度计算方法,其中具有代表性的有渐近均匀化法[3-7]、多尺度有限元法(MsFEM)[8-10]、非均质多尺度法(HMM)[11-12]、代表体元法(RVE)[13-15]、小波均匀化方法[16]等。这些方法通常是从宏观域中取出有代表性的体元(微观域),在此体元上构建一个局部边值问题,在得到体元的等效力学参数后,将原结构等效成具有此参数的均匀结构求解宏观域的力学响应。一般来说,选择局部问题边界条件具有较强的主观性和经验性,对计算精度具有显著影响[9-10],因此构造局部问题合适的边界条件是多尺度计算的重点和难点之一。另一方面,虽然这些多尺度方法均可用于分析结构的宏观力学行为,但通常难以得到结构的微观力学响应(如局部应力和应变等)[2,11],在很多情况下获得全域精细网格解是至关重要的,如结构强度,疲劳和断裂分析等.

作者曾基于有限元子结构方法提出了有限细胞法(FCM),用于求解表面结构的多尺度润滑问题(标量场问题)效果良好[17-18]。该方法的基本思想与传统多尺度方法类似,亦是先构建微观域的局部问题,后求解宏观域整体响应。主要不同点在于:①构建局部问题时,无需引入微观边界条件,避免了人为选择的主观性和经验性;②直接通过矩阵运算得到粗网格(细胞)的刚度矩阵和载荷向量,而不是得到微观等效材料参数后,再构建宏观单元的刚度矩阵;③易于降尺度计算。

为对非均质多尺度复合材料进行结构分析,本文以二维连续体问题分析为例,介绍FCM求解矢量场问题的基本原理及其实施过程,并通过几个有代表性的数值算例说明其有效性。限于篇幅,本文只介绍FCM的基本原理及其在复合材料力学分析中的应用,多尺度润滑问题的分析可参见文献[17-18],有关FCM在多孔介质渗流、传热等问题中的应用将另文论述。

1 有限细胞法

假定有结构如图1所示,若将最小的重复单位定为细胞,则该结构由4个细胞构成,整体域可由方形细胞和圆形细胞两种组合而成。通常FCM的实施包括以下4个步骤,如图2所示。

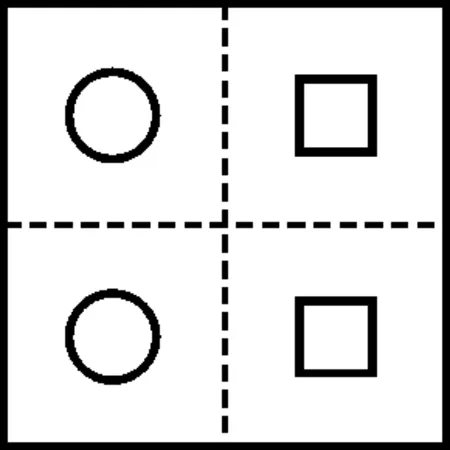
图1 宏观域结构示意图

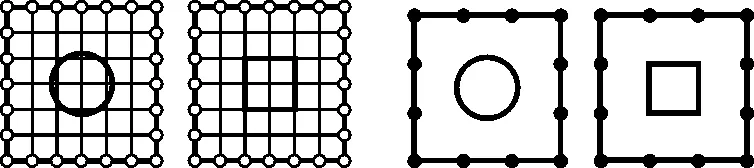
(a)凝聚细胞内部自由度 (b)凝聚细胞边界自由度

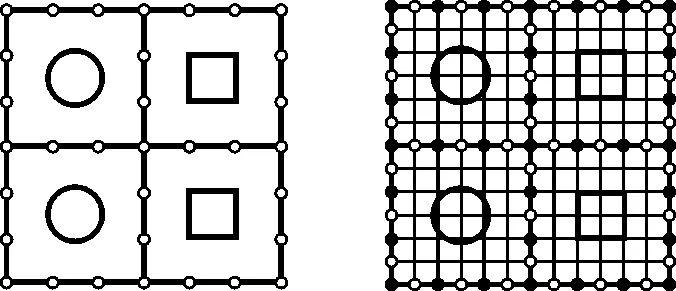
(c)求解宏观域响应 (d)降尺度计算 图2 有限细胞法关键步骤

1.1 凝聚细胞内部自由度

为便于说明,使用双线性四边形单元对细胞进行结构化网格剖分,每个方向均具有M个节点,如图2a所示。使用常规有限元法组装得到细胞整体刚度矩阵和载荷向量,细胞的平衡方程可以表示为

Kcuc=fc

(1)

式中:Kc表示细胞的刚度矩阵;uc表示细胞所有节点的自由度;fc表示载荷向量;下标c表示细胞。需要说明的是,在建立局部问题(细胞平衡方程)时,无需施加边界条件。对于弹性力学问题fc是具有2M2个0元素的列向量,但对于传热、渗流或润滑等问题,fc不一定是零向量。经过适当的节点编号,式(1)可用矩阵分块表示为

(2)

式中:下标b表示细胞边界;i表示细胞内部;ub表示细胞边界上的自由度;ui表示细胞内部的自由度。基于消去法对ui凝聚,式(2)可表示为

(3)

(4)

(5)

1.2 凝聚细胞边界自由度

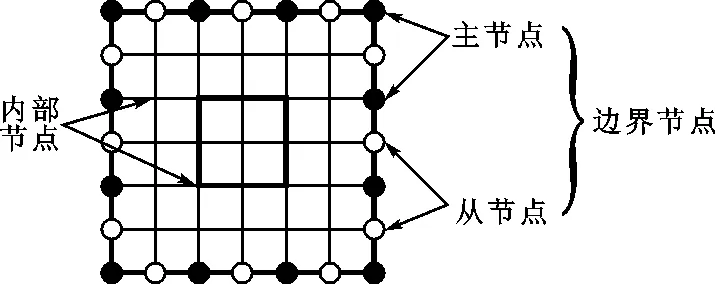
图3 细胞节点分类

为进一步减小细胞的等效刚度矩阵,在细胞的4条边界上分别选取保留均布的k个主节点,边界上的其余节点定义为从节点,如图2b所示,节点分类如图3所示。若假定主节点的自由度已知,则从节点的自由度可通过k个主节点的自由度插值计算得到。为方便实施,使用拉格朗日p次多项式作为插值函数,其中p≤k-1。例如,从节点中的第l个自由度可由同侧边界上的p+1个主节点的对应自由度插值得到

(6)

式中:下标s表示从节点;m表示主节点;φj表示拉格朗日插值基函数。将式(6)改写为向量形式

(7)

通过矩阵叠加,全体从节点自由度可表示为

us=Tum

(8)

(9)

式中:T表示插值矩阵。

根据主节点与从节点的分类,式(3)可以用矩阵分块表示为

(10)

将式(8)代入到式(10),可得

(11)

式中:I表示单位矩阵。式(11)第一行可表示为

Kmum=fm

(12)

Km=kmm+kmsT

(13)

即细胞的等效刚度矩阵和载荷向量分别可用Km和fm表示。在此凝聚过程中使用主节点的自由度插值计算从节点的自由度,忽略了部分信息,计算精度会有所损失,但通常在细胞边界上的节点的自由度不会产生间断或突变,当在细胞边界上保留较多的主节点和选取高阶插值函数后,这时精度损失变得可以忽略。一般来说,线性和二次插值函数通常误差较大,当插值函数的阶数高于三次后,计算误差会显著降低。本文将在数值算例部分详细讨论FCM插值方案对计算精度的影响。另一方面,经过插值近似,细胞待求的自由度取决于主节点的数量,即8(k-1),对于固体力学问题,当细胞边界上保留11个主节点时,FCM与FEM精细网格间计算结果之间的误差已经低于1%,此时细胞的等效刚度矩阵Km为80×80稠密矩阵。通过两个凝聚步骤得到规模较小细胞等效刚度矩阵和载荷向量是有限细胞法的关键步骤。对于周期性结构,细胞的刚度矩阵仅需计算一次,对于非周期结构细胞刚度矩阵需要分别计算,但不同细胞的刚度矩阵的计算完全独立,因此易于并行。

1.3 求解宏观域响应

如图2c所示,宏观域可以认为由有限个细胞组成。在得到的等效细胞刚度矩阵Km和载荷向量fm后,系统的总体刚度矩阵和载荷向量可表示为

Kum=f

(14)

(15)

式(15)表示系统总体刚度矩阵由每个细胞的等效刚度矩阵组装而成。施加宏观边界条件后,式(14)可解,从而得到宏观域细胞主节点的自由度。

1.4 降尺度计算

对比于传统多尺度方法(均匀化,MsFEM和HMM等),FCM能很容易地进行降尺度计算,且可以保证在细胞边界处自由度连续。如图2d所示,在得到主节点的自由度后,从节点的自由度可由式(8)计算得到,由此便得到了细胞的边界自由度ub,而细胞内部的自由度为

(16)

至此整体域精细网格的全部自由度均已求出,应力和应变等信息可用传统有限元方法计算得到。

从以上推导过程可以看出:有限细胞法完全基于矩阵变换,无需引入微观边界,易于降尺度计算;同时该方法与控制方程的无关,因此易于将其推广至非线性结构分析、热分析、地下水渗流等领域。

2 数值算例

本节将以几个典型的算例来验证有限细胞法的计算精度和计算效率等问题,所有计算均在个人台式机上完成(CPU 3.2 GHz,RAM 16G),单核计算,编程语言为MATLAB 8.3,操作系统为Windows 7(64 bit)。多尺度精细网格解用FCMk×p表示,k表示细胞单侧边界上的节点个数,p表示拉格朗日插值函数的阶次,把传统有限元法精细网格解作为参考解,用FEM表示。算例中的所有参数都假设是无量纲量,且本文考察的是平面应力情况。

2.1 算例1

算例1为均质材料悬臂梁结构分析。为了验证FCM的正确性,构造一个简单的具有矩形截面的均质悬臂梁算例,如图4所示,悬臂梁结构的右端固定支撑,左端承受P=100的分布力,悬臂梁长度L=100,高度h=10,宽度为1,材料的弹性模量为2×105,泊松比为0.3。悬臂梁中性轴挠度的理论表达式为[19]

(17)

图4 均质悬臂梁结构示意图

本算例中FCM使用了6×5的插值方案,即在细胞的每条边界上保留了6个主节点,从节点的自由度使用5次拉格朗日函数由主节点自由度插值得到。FCM使用40×40的均布双线性四边形单元对细胞进行划分,采用20×2的细胞对全域进行划分,故全域细网格尺度共有8 000×800单元,有限元采用相同的细网格密度。通过L2范数[12]验证数值方法的实际效果

(18)

式中:Q为悬臂梁中性轴相应的细网格节点数。本算例中vref取解析解va,即式(17)。悬臂梁中性轴y向位移对比如图5所示。由FCM和FEM的L2范数分别为3.15×10-3和3.35×10-3可以发现,对于均质材料结构FCM在相同的细网格尺度上可以得到比传统FEM更高的精度,且收敛于精确解。同时,FCM的计算时间仅为FEM的26.2%,计算效率也更高。

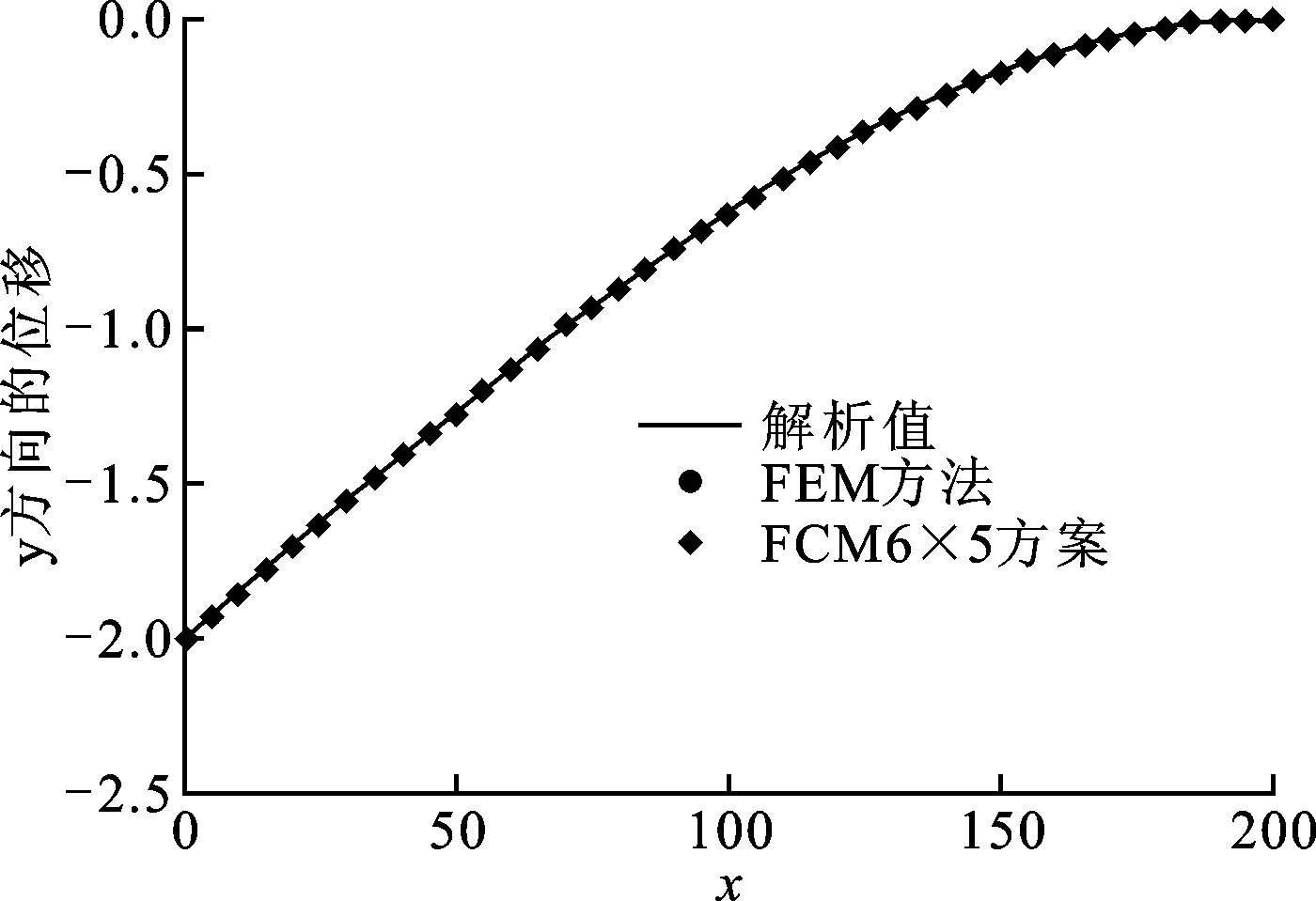
图5 均质悬臂梁中性轴y向位移比较

2.2 算例2

算例2为具有周期结构的非均质悬臂梁结构分析。悬臂梁模型及其边界条件如图6所示。该结构由A×B个材料相同的正方形细胞组成,本算例中考虑了5种A×B的组合,即6×2、12×3、18×7、24×13、30×29和40×30,细胞中的边长为1,包含边长为0.3的正方形强化相。其中,基体材料的弹性模量为2×104,泊松比为0.3。强化相的弹性模量为2×105,泊松比为0.25,细胞采用40×40的均匀双线性四边形网格划分,如图7所示。悬臂梁左端固定,上端承受强度q=1的均布载荷。

图6 复合材料结构示意图

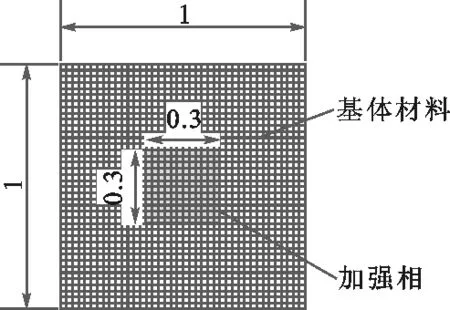
图7 细胞网格划分

本算例中考虑了FCM的两种插值方案,分别为6×5和11×9,不同计算规模下,FEM和FCM计算结果的比较如表1所示。本算例中取相同网格密度下FEM的计算结果作为参考解,当A=12、B=3时,悬臂梁中性轴y向位移对比如图8所示。

从表1可以看出,FCM和FEM的计算结果吻合良好,FCM 6×5方案的L2范数最大误差为22.8×10-3,而FCM 11×9方案的L2范数最大误差仅为2.43×10-3。总体看来,FCM 11×9方案的计算结果优于FCM 6×5方案。这是因为在边界上保留更多的主节点和采用高次的插值函数,从而可以更精确地计算从节点的自由度。对于结构分析来说,细胞单侧边界上保留11个主节点,FCM已经具有足够高的精度,保留更多的主节点并不能继续有效提高精度,但会增加计算时间和内存。因此,综合考虑精度和效率,在后续的算例中FCM将采用11×9的插值方案。

图8 悬臂梁中性轴y向的位移比较(A=12,B=3)

A×B总自由度/103L2范数/10-3FCM6×5FCM11×9计算时间/sFCM6×5FCM11×9FEM6×238.46.262.4301.982.673.2312×311522.800.1732.063.499.7218×740311.000.3083.393.9235.1024×139986.910.3364.516.36118.8030×2927844.300.4096.9615.10851.0040×3038405.540.1857.7521.101643.50

在计算时间方面,随着总自由度的增加,传统有限元方法的计算时间显著增加,当总自由度达到380万时,FEM的计算时间接近0.5 h,且内存消耗也接近于物理内存极限(16 GB),因此我们没有尝试更大规模的计算,但在相同的网格密度下FCM的计算时间均不足22 s,内存需求也非常低(小于1 GB)。这是因为对于周期结构,细胞的刚度矩阵仅需构造一次,且规模较小,故对于周期性结构,有限细胞法可显著降低计算量,节省内存,扩大了计算规模,具有明显的优势。

2.3 算例3

算例3为非完全周期结构的非均质悬臂梁结构分析。悬臂梁由30×6个细胞组成,如图9所示。细胞的几何尺寸、网格划分、材料性质和结构的边界条件与算例1相同,但在竖直方向上,复合材料增强相的边长由0.1变化到0.6,步长为0.1。

图9 非均质悬臂梁模型

(a)FEM

(b)FCM图10 宏观von Mises应力云图比较

(a)FEM (b)FCM 图11 左下角细胞微观尺度von Mises应力云图比较

图12 悬臂梁中性轴y方向的位移比较

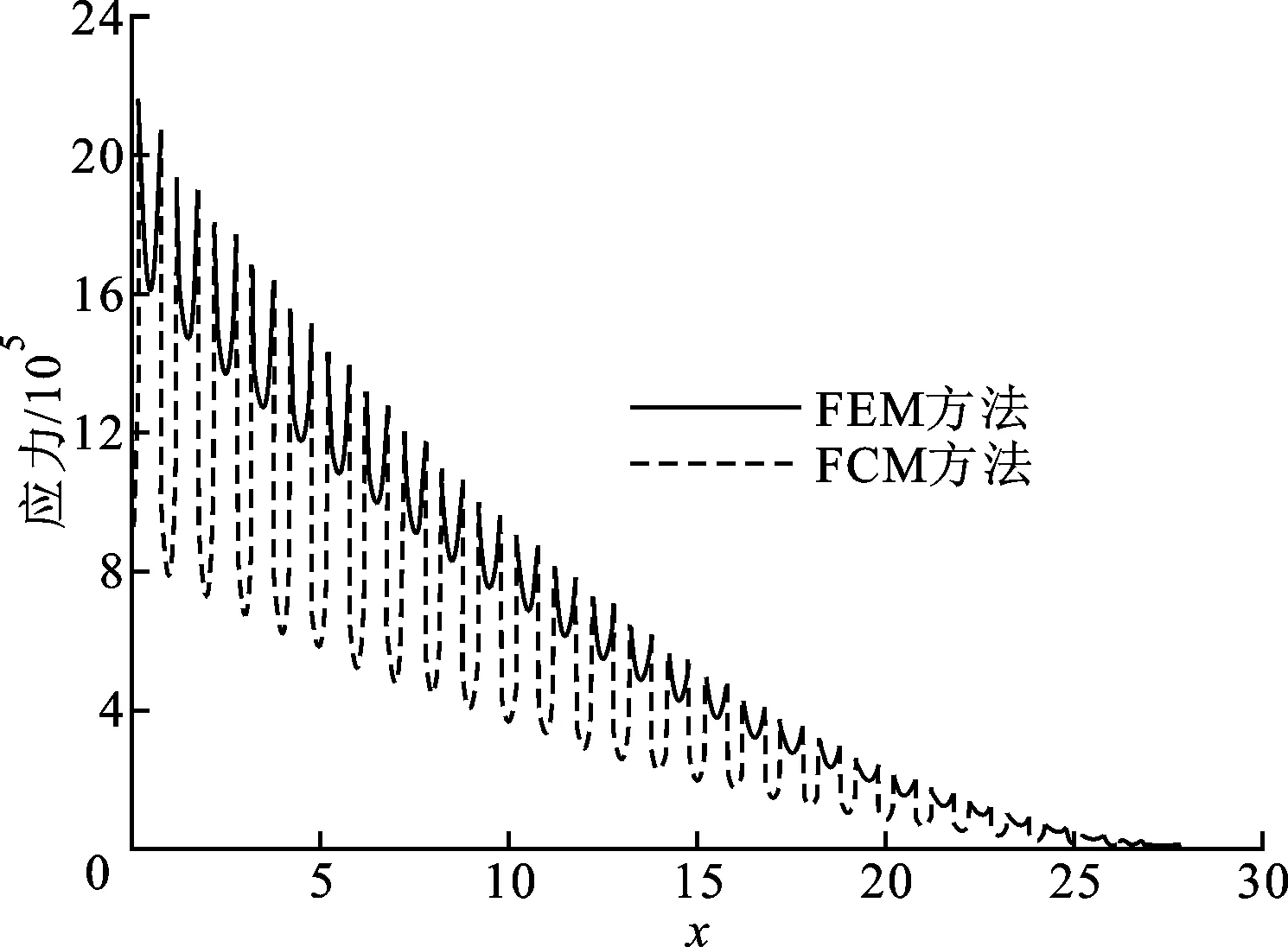
图13 过应力最大点轴线方向von Mises应力比较

von Mises整体应力对比如图10所示,细胞微观尺度von Mises应力云图如图11所示,悬臂梁中性轴y向位移比较如图12所示,过应力最大点轴线方向von Mises应力比较如图13所示,发现FCM的计算结果与FEM参考解吻合良好。注意到悬臂梁底部增强相尺寸已经接近于细胞尺寸,在这种情况下一些传统多尺度计算方法(均匀化,MsFEM等)的计算精度会急剧下降,但从图10至图13可以看到,FCM与FEM的结果依然高度吻合,说明FCM具有良好的适应性和灵活性。在计算时间方面,本算例中总自由度为57.6万,FEM的计算时间为50.2 s,而FCM的计算时间仅为13.3 s,说明FCM在非完全周期情况下依然具有很高的计算精度和较高的计算效率。

若宏观结构没有任何的周期性,传统有限元方法可能因为计算时间和内存需求过大而无法计算,但有限细胞法可以将原问题分解为很多小问题后分别求解,且不同细胞刚度矩阵的构造完全独立,易于将细胞刚度矩阵的构造进行并行化处理,且不同线程之间的通信代价极低,因此FCM为分析非均质非周期多尺度材料的力学性能提供了一种方法。

3 结 论

本文介绍了有限细胞法(FCM)的基本原理,详细阐述了该方法的理论基础和关键实施步骤,展示了其在复合材料结构分析中的应用。FCM的基本思想是通过矩阵运算直接得到多节点的粗网格(细胞)刚度矩阵,在求解得到粗网格尺度的力学响应后,通过降尺度计算到全域精细网格尺度的响应。通过数值算例验证有限细胞法的计算精度和计算效率等问题,结果表明,相对于传统FEM,FCM可显著提高计算效率,节省内存,扩大计算规模,尤其是对于周期材料,优势非常明显。相对于经典多尺度方法,FCM在构建局部问题时无需引入微观边界条件,易于进行降尺度计算,且具有与控制方程无关、方便实施等优点。FCM与控制方程无关的特性决定了其易于推广至多尺度的非线性结构分析、热分析、地下水渗流等领域。

[1] ROUET-LEDUC B, BARROS K, CIEREN E, et al. Spatial adaptive sampling in multiscale simulation [J]. Computer Physics Communications, 2014, 185(7): 1857-1864.

[2] KANOUTÉ P, BOSO D P, CHABOCHE J L, et al. Multiscale methods for composites: a review [J]. Archives of Computational Methods in Engineering, 2009, 16(1): 31-75.

[3] FISH J, SHEK K, PANDHEERADI M, et al. Computational plasticity for composite structures based on mathematical homogenization: theory and practice [J]. Computer Methods in Applied Mechanics and Engineering, 1997, 148(1): 53-73.

[4] 易垒, 文毅. 惯性载荷作用下火箭橇结构拓扑优化设计 [J]. 应用力学学报, 2013, 30(1): 80-85 YI Lei, WEN Yi. Topology optimization of rocket sled structure under inertial loads [J]. Chinese Journal of Applied Mechanics, 2013 , 30(1): 80-85.

[5] MIEHE C C B. On multiscale FE analyses of heterogeneous structures: from homogenization to multigrid solvers [J]. International Journal for Numerical Methods in Engineering, 2007, 71(10): 1135-1180.

[6] ZHANG H W, ZHANG S, BI J Y, et al. Thermo-mechanical analysis of periodic multiphase materials by a multiscale asymptotic homogenization approach [J]. International Journal for Numerical Methods in Engineering, 2007, 69(1): 87-113.

[7] 张洪武, 张盛, 毕金英. 周期性结构热动力时间空间多尺度分析 [J]. 力学学报, 2006, 38(2): 226-235. ZHANG Hongwu, ZHANG Sheng, BI Jinying. Thermodynamic analysis of multiphase periodic structures based on a spatial and temporal multiple scale method [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2): 226-235.

[8] HOU T Y, WU X H. A multiscale finite element method for elliptic problems in composite materials and porous media V. Journal of Computational Physics, 1997, 134(1): 169-189.

[9] 张洪武, 吴敬凯, 刘辉, 等. 扩展的多尺度有限元法基本原理 [J]. 计算机辅助工程, 2010, 19(2): 3-9 ZHANG Hongwu, WU Jingkai, LIU Hui, et al. Basic theory of extended multiscale finite element method[J]. Computer Aided Engineering, 2010, 19(2): 3-9.

[10]ZHANG H, WU J, LÜ J, et al. Extended multiscale finite element method for mechanical analysis of heterogeneous materials [J]. Acta Mechanica Sinica, 2010, 26(6): 899-920.

[11]E Weinan, ENGQUIST B, LI X, et al. Heterogeneous multiscale methods: a review [J]. Communications in computational physics, 2007, 2(3): 367-450.

[12]E Weinan, ENGQUIST B, HUANG Z. Heterogeneous multiscale method: a general methodology for multiscale modeling [J]. Physical Review: B, 2003, 67(9): 092101.

[13]XIA Z, ZHOU C, YONG Q, et al. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites [J]. International Journal of Solids and Structures, 2006, 43(2): 266-278.

[14]LI X, LIU Q, ZHANG J. A micro-macro homogenization approach for discrete particle assembly Cosserat continuum modeling of granular materials [J]. International Journal of Solids and Structures, 2010, 47(2): 291-303.

[15]PECULLAN S, GIBIANSKY L V, TORQUATO S. Scale effects on the elastic behavior of periodic and hierarchical two-dimensional composites [J]. Journal of the Mechanics and Physics of Solids, 1999, 47(7): 1509-1542.

[16]DOROBANTU M, ENGQUIST B. Wavelet-based numerical homogenization [J]. SIAM Journal on Numerical Analysis, 1998, 35(2): 540-559.

[17]裴世源, 徐华, 马石磊, 等. 多尺度表面织构流体润滑问题的快速求解方法 [J]. 西安交通大学学报, 2011, 45(5): 119-126. PEI Shiyan, XU Hua, MA Shilei, et al. Multiscale method for modeling surface texture effects in hydrodynamic lubrication regime [J]. Journal of Xi’an Jiaotong University, 2011, 45(5): 119-126.

[18]PEI S, MA S, XU H, et al. A multiscale method of modeling surface texture in hydrodynamic regime [J]. Tribology International, 2011, 44(12): 1810-1818.

[19]TIMOSHENKO S, GOODIER J N. Theory of elasticity [M]. New York, USA: McGraw-Hill, 1951: 506.

(编辑 杜秀杰)

Deterministic Multiscale Method for Heterogeneous Composite Material

PEI Shiyuan1,XU Hua1,2

(1. Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System, Xi’an Jiaotong University,Xi’an 710049, China; 2. School of Mechanical Engineering, Xinjiang University, Urumqi 830046, China)

For the strength analysis of heterogeneous materials in elasticity, a deterministic multiscale calculation method, finite cell method (FCM), is presented. The condensation and interpolation technique are adopted to obtain the coarse element stiffness matrix, then the original problem can be solved in coarse-scale, and the fine-scale solution can be sought out by back substitution. The comparison with analytic method and finite element method (FEM) on several numerical examples indicates that FCM enables to significantly expand computational scale and greatly improve computing rate. In FCM, the artificial boundary conditions are unnecessary for constructing macroscopic meshes, and the downscaled computing can be easily performed. FCM is also feasible for non-linear multiscale structure analysis, thermal analysis and porous flow analysis.

finite cell method; multiscale computation; heterogeneous material

2015-01-13。

裴世源(1983—),男,讲师。

国家重点基础研究发展计划资助项目(2011 CB706602);陕西省科技攻关资助项目(2015GY022)。

时间:2015-06-29

10.7652/xjtuxb201510002

TP301.6

A

0253-987X(2015)10-0008-06

网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150629.1137.003.html