时滞系统的二自由度Smith 预估控制研究

信 芳，何建忠

(上海理工大学 光电信息与计算机工程学院，上海 200093)

1982 年Garcia 和M.Morari 完整地提出并发展了内模控制策略，内模控制结构简单、参数整定直观明了、鲁棒性强、控制性能良好，近年来在过程控制系统中得到了广泛应用［1－3］。常规内模控制器只有一个可调参数，是一种一自由度控制器，不具备使系统同时获得良好目标值跟踪特性和干扰抑制特性的能力，参数整定时一般要在系统的目标值跟踪特性和干扰抑制特性之间进行折中选择，这样做一般能满足大多数控制系统的要求，但对于高性能的控制系统则有一定的局限性，难以兼顾各方面的性能要求而获得满意的控制效果;采用二自由度控制结构则可同时独立地调节目标值跟踪特性、干扰抑制特性和鲁棒性，使各方面的性能均达到最佳。

本文从内模控制原理出发，将Smith 预估控制与内模控制相结合，针对典型的大时滞稳定过程提出一种二自由度Smith 预估控制方法，将系统的设定值跟踪特性和干扰抑制特性解耦，通过控制器的设计，使系统同时获得良好的设定值跟踪特性、干扰抑制特性和鲁性。

1 常规内模控制

内模控制基本结构框图如图1 所示［4］。

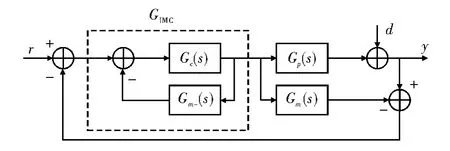
图1 内模控制结构框图

其中r，u，y 分别为给定输入、控制量和输出;d 为干扰输入;Gp(s)为实际被控过程对象;Gm(s)为被控过程的数学模型;GIMC(s)是内模控制器;Gc(s)是反馈控制器;Gf(s)是扰动传递函数。

由图1 可知

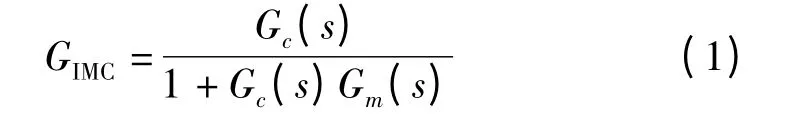
内模控制器设计分为两步进行。首先设计一个稳定的理想控制器，而不考虑系统的鲁棒性和约束;其次引入滤波器，通过调整滤波器的结构和参数来获得期望的动态品质和鲁棒性。

(1)对模型对象Gm(s)进行分解。对象模型

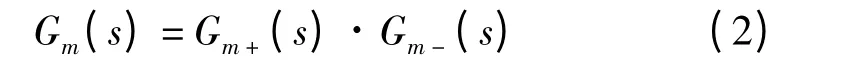
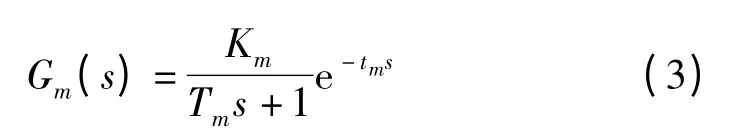
(2)内模控制器设计。

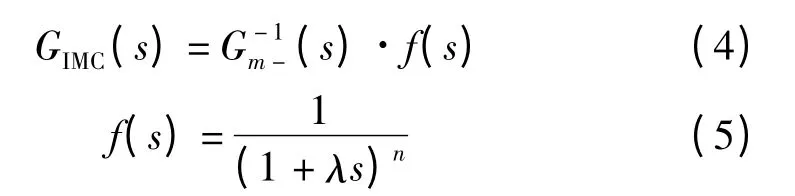
式中，f(s)为低通滤波器;n 为对象模型Gm(s)的相对阶次;λ 为滤波器时间常数。

将式(4)代入式(5)得

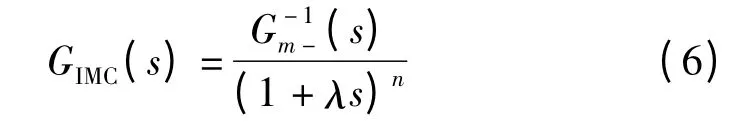
由式(1)可知

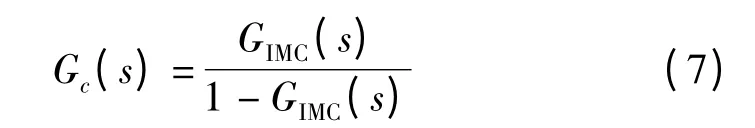
将式(6)代入式(7)可得

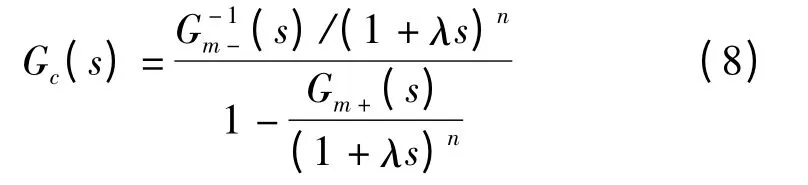
理想的PID 控制器具有以下算式。

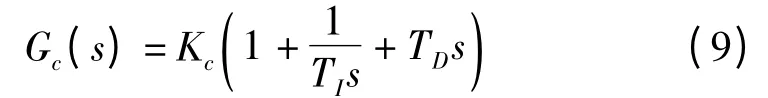
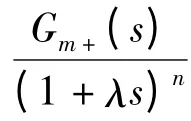
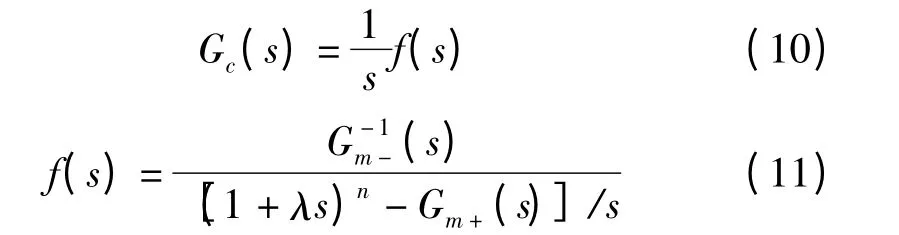
将f(s)进行Taylor 级数展开，可得到

令

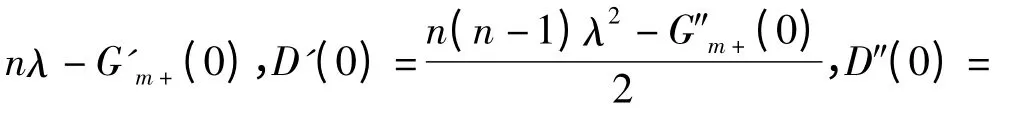
由以上3 式可得f(s)及其一、二阶导数在s=0 处的值。最终得出PID 控制器的参数为［5］

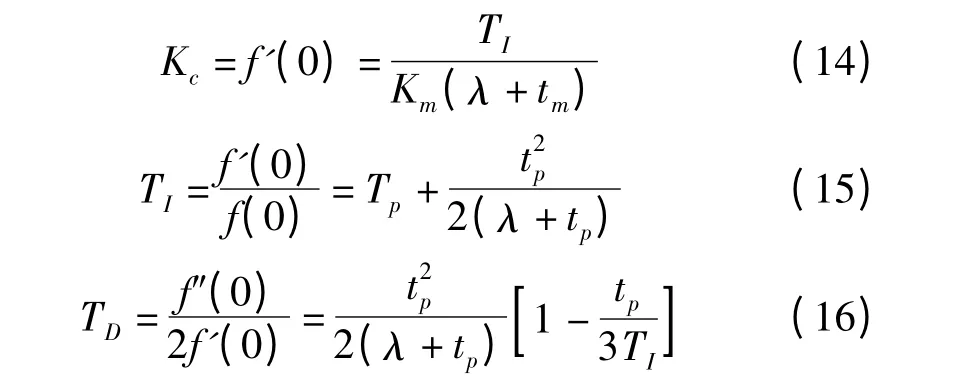
2 二自由度Smith 预估控制结构

图2 为二自由度Smith 预估控制系统结构图［6－7］，其中Q(s)是干扰抑制控制，Gc(s)是设定值跟随控制器［8－10］。

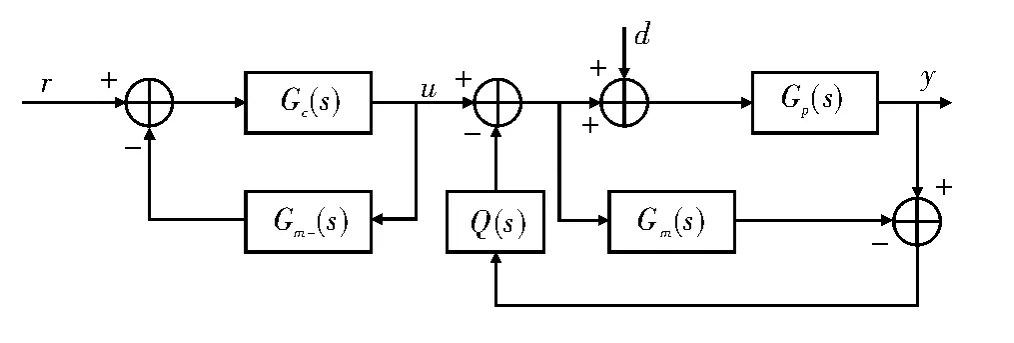
图2 二自由度Smith 预估控制系统结构图

由图2 得出设定值输入和干扰输入到过程对象输出的闭环传递函数为

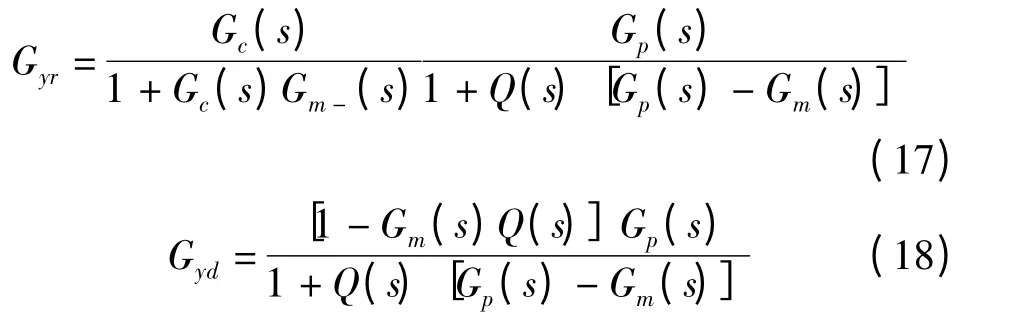
当模型精确即Gp(s)=Gm(s)时，有

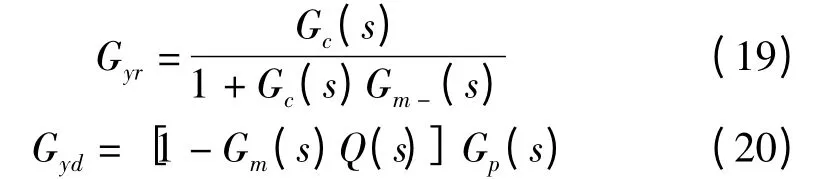
由式(19)和式(20)可看出，Gyr(s)与Gyd(s)实现完全解耦，这使得设定值跟随控制器Gc(s)和干扰抑制控制器Q(s)可独立设计。干扰抑制特性Gyd(s)与Q(s)有关，设定值跟踪特性Gyr(s)与Gc(s)有关，使系统获得良好的设定值跟随特性和干扰抑制特性，无需在两种特性之间进行选择。此外，通过Q(s)的设计可使系统具有良好的鲁棒性。

(1)设定值跟随特性设计。利用上述内模控制中求取反馈控制器的方法获取设定值跟随控制器。即利用Taylor 级数展开，对被控对象的大时滞环节进行近似处理，再结合已知的被控对象模型参数来求解PID控制器的增益、积分时间和微分时间等参数［11］。

(2)干扰抑制特性。对于一阶惯性加纯滞后系统，选择低通滤波器

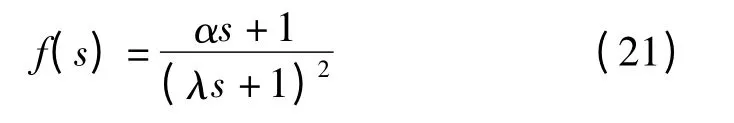
式中，λ 是滤波时间常数;α 是待定系数。

根据式(18)确定α 使(1－GmQ)的零点对消Gp(s)中的惯性环节对应的极点，可以改进干扰抑制性能，由式(22)求取α。

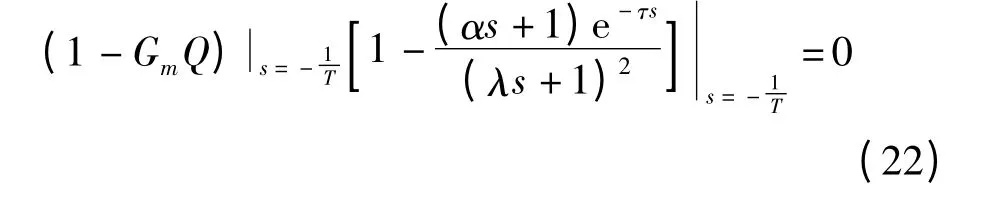
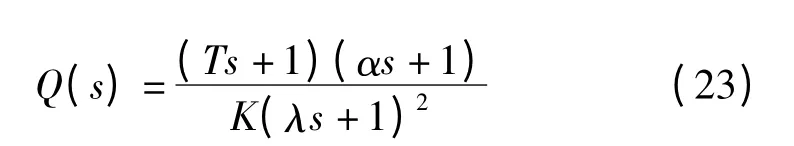
综上可知，分别改变设定值跟随控制器和干扰抑制控制器的滤波时间参数，可独立调整系统的目标值跟踪特性和干扰抑制特性。

3 仿真

以工业过程控制领域中常见的一阶惯性加纯滞后系统为被控对象，对所提出的Smith 二自由度内模控制方法进行仿真研究，并与内模控制方法对比。

从图中可看出，本文方法较好地改善了系统的干扰抑制特性。尤其当模型失配时目标跟踪值特性和干扰抑制特性得到了较好的体现。通过合理的选择λ1和λ2可使系统同时获得良好的目标值跟踪特性、干扰抑制特性和鲁棒性，从而克服常规内模控制的不足。

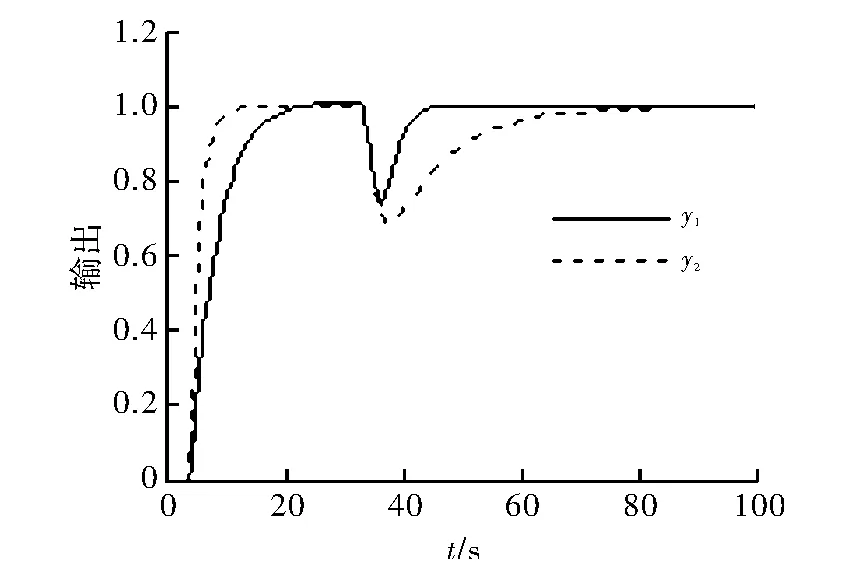
图3 模型精确时的阶跃响应曲线

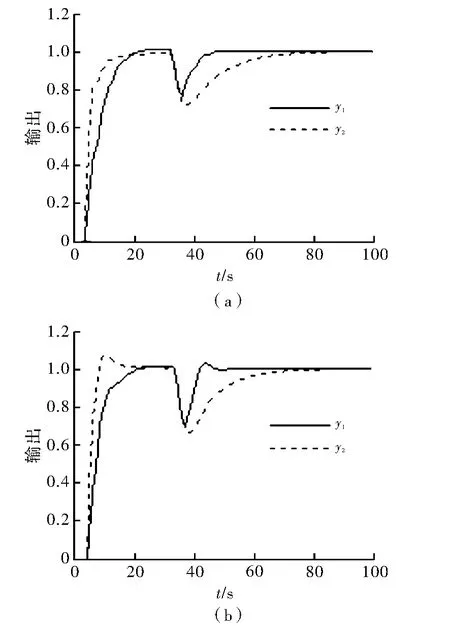
图4 模型失配时的阶跃响应曲线

4 结束语

提出的二自由度Smith 预估控制方法改善了系统抑制干扰的特性，设定值跟踪响应与扰动响应分离使跟踪控制器和扰动控制器可独立设计，通过两个参数的调整，可使系统同时具有良好的目标值跟踪特性、干扰抑制特性和鲁棒性。

［1］ Morari M.Robust process control［M］.Englewood Cliffs，New Jersey:Prentice－Hall，1989.

［2］ Zafirion E.Internal model control:robust digital controller synthesis for multivariable open loop stable or unstable processes［J］.International Journal of Control，1991，54(3):665－704.

［3］ Vandenrsen J M.Internal model control with improved disturbance rejection［J］.International Journal of Control，1995，62(4):983－999.

［4］ 鲁照权，韩江洪.一类大时滞过程的内模预测控制［J］.合肥工业大学学报:自然科学版，2001，24(1):1－5.

［5］ 刘洋，王钦若.基于内模控制的PID 参数整定及仿真［J］.广东工业大学学报，2008，25(1):64－68.

［6］ 张井岗，李临生，陈志梅，等.二自由度PID 调节器的内模整定方法［J］.仪器仪表报，2002，23(1):28－30.

［7］ 张井岗.二自由度控制［M］.北京:电子工业出版社，2012.

［8］ 赵辉.基于内模控制原理的PID 控制器设计［D］.天津:天津大学，2005.

［9］ 刘金琨.先进PID 控制Matlab 仿真［M］.北京:电子工业出版社，2004.

［10］舒迪前.预测控制系统及其应用［M］.北京:机械工业出版社，1996.

［11］Zhang W D，Sun Y X.Two degree of freedom smith predictor for processes with time delay［J］.Automatica，1998(34):1279－1282.