基于OpenMP 的色散介质FDTD 并行程序设计

刘 珺，赵志钦

(电子科技大学 电子工程学院，四川 成都 611731)

时域有限差分(Finite Difference Time Domain，FDTD)方法，在1966 年，由K.S.Yee 首次提出。该方法是求解麦克斯韦微分方程组的时域方法，因此可处理复杂形状目标和非均匀介质物体的电磁散射、辐射问题。作为时域方法，FDTD 可以通过傅里叶变化，处理一个频带内的电磁透射、散射等问题。与频域方法相比，在处理宽频带的问题时，FDTD 具有明显的速度优势。现实中具有众多色散介质模型，本文介绍了非磁化等离子体模型，针对这类色散模型，可采用PLRCFDTD 方法［1］处理。但是，对于色散介质，FDTD 的网格尺寸要小于波长的1/40 才能保证不会发生数值色散［2］，这就导致了时间步长的缩短，同时增加了迭代所需的时间步数目。加之使用线性递归卷积方法处理色散介质，会大幅增加每一时间步内电场迭代的计算量。为了减少求解时间，可在FDTD 处理色散介质的过程中引入并行求解方法。

目前，并行算法的实现主要基于两种标准:(1)基于分布式内存模型的MPI 标准［3］;(2)基于共享式内存模型的OpenMP 标准［4］。MPI 标准下，各个处理单元具有各自独立的局部储存器，由于不存在公共可用的存储单元，各处理器之间通过消息传递来交换信息，控制并行任务的执行。OpenMP 标准下，各个处理单元通过对共享内存的访问来实现信息的交换、任务的并行。

本文先以三维非磁化等离子体为例，给出了处理色散介质的线性递归卷积(PLRC)方法。之后介绍了OpenMP 方法以及在色散介质时域有限差分方法求解中的具体实现步骤。最后计算了经过OpenMP 方法并行加速后，在5 ～25 GHz 频率范围内的电磁波对非磁化等离子体的透射衰减，并对比了使用OpenMP 方法加速前后的计算时间。通过实验验证了该并行算法的有效性。

1 色散介质FDTD 方法

1.1 色散介质基本模型

各向同性介质的麦克斯韦旋度方程表达式为［5］

对于色散介质，其本构参数随时间变化而变化，这里假定介质的磁本构参数与频率无关，只有介电系数与频率有关。给出频域的本构关系式

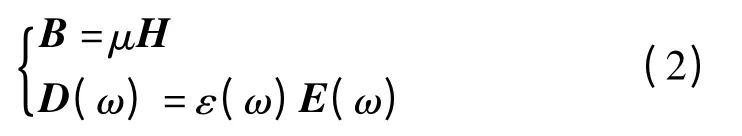
本文研究的非磁化等离子体属于Drude 模型，其形式为

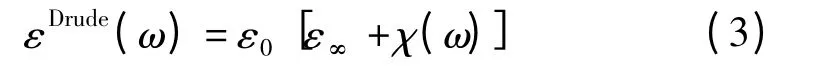
1.2 PLRC－FDTD 方法

本文采用分段线性递归卷积时域有限差分方法(PLRC－FDTD)。与传统的线性递归卷积时域有限差分(RC－FDTD)相比，PLRC－FDTD 假设每个网格的场值是线性变化的，这使得PLRC－FDTD 的计算精度相对于RC－FDTD 来说有了较大改善。在PLRCFDTD 中，卷积项中的电场场值在每一时间步长上是线性变化的。这里给出Ei+1、Ei、t 的函数

将时间离散，结合式(4)代入式(3)，得

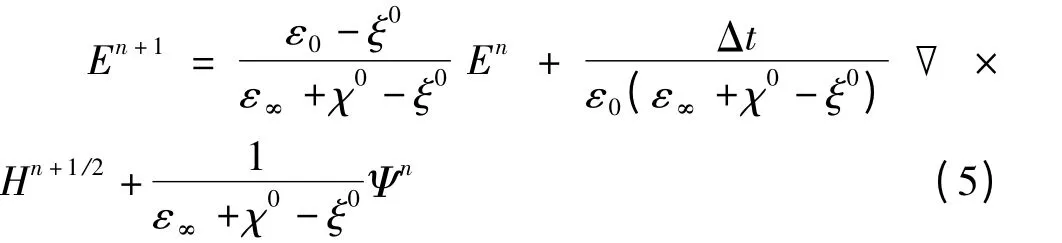
以上是非磁化等离子体中电场的迭代方程，磁场的迭代方程与传统FDTD 方法一致。

2 OpenMP 并行设计

2.1 OpenMP 概述

OpenMP 本身并不是一种独立的语言，而是对常用科学计算语言(C/C++、Fortran)的一种补充和扩展。OpenMP 通过编译指导指令和应用程序编程接口(API)来实现共享内存的多线程并行计算。

2.2 OpenMP 并行模型

OpenMP 的执行模型采用fork－join 的形式，其中fork 创建新线程或者唤醒已有的线程;join 即多线程的会合。fork－join 执行模型在刚开始时，只有一个被称为“主线程”的线程存在。在程序运行中，当需要进行并行计算时，则会调用新的线程去执行并行任务。在执行并行计算时，主线程与调用的新线程同时工作。当并行任务结束时，被主线程调用的新线程退出，主线程依旧单独工作。因而，在成对的fork 和join 之间的区域就是并行域，放置需要并行执行的代码。

图1 fork－join 并行执行模型

OpenMP 中常用的两种并行策略［6］:数据并行和功能并行。数据并行常使用for/parallel for 指令制导，功能并行常使用sections/parallel sections 指令制导。

FDTD 的迭代方式是蛙跳式(forg－leap)En→Hn→En+1→Hn+1，在每一时间步内，电场的迭代与磁场的迭代相对独立，即在同一时间步内，只更新电场、磁场中的一项，另一项保持不变。这样的迭代方式适合与并行计算。

在此选用数据并行的策略，采用for 与parallel for指令混合制导。

3 并行FDTD 性能分析

3.1 数值算例

首先，验证OpenMP 并行算法应用到色散介质FDTD 方法时的准确性。这里以电磁波在三维分层非磁化等离子体中传播为例。入射波为平面波，频率范围在5 ～25 GHz，空间步长Δ=0.5 mm，时间步长Δt=0.83 ps，由连接边界条件引入。设置分层非磁化等离子体，尺寸为5 cm×5 cm×5 cm，沿入射方向分为3层。第1 层厚度为1.25 cm，等离子体参数为ωp=17.16 Grad/s，υ=6 GHz;第2 层厚度为2.50 cm，等离子体参数为ωp=25.74 Grad/s，υ=6 GHz;第3 层厚度为1.25 cm，等离子体参数为ωp=17.16 Grad/s，υ=6 GHz。在等离子体背对来波方向面的中心，设置一个观测点，对记录的透射波信号作傅里叶变换，求得5 ～25 GHz 频带内相对于入射信号振幅的衰减情况，并将OpenMP 并行计算的结果同CST 的仿真结果进行对比，结果如图2 所示。由对比可知，加入OpenMP 并行算法后的计算结果与实际情况相符，OpenMP 并行求解色散介质的方法具有较高的数值精度。

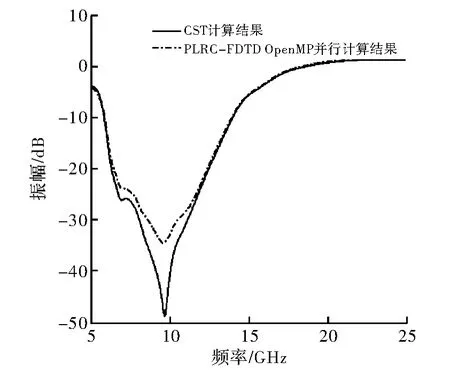
图2 分层非磁化等离子体并行算例

3.2 并行性能分析

首先，给出两个衡量并行性能的指标，加速比和效率［7］。

加速比:单个线程运行程序花费的时间与n 个线程参与运行程序花费时间的比值;效率:加速比与n 的比值。

为了计算OpenMP 并行算法对于色散介质FDTD方法的并行性能，这里给出了3 组计算区域大小不同的模型，计算结果收敛所需的迭代运行的次数分别为500 次、1 000 次、2 000 次，分别计算3 组模型的加速比和效率，3 组模型在并行计算是均占用5 个线程，计算结果如表1 所示。

表1 非磁化等离子体算例的加速比和效率

4 结束语

本文利用OpenMP 编程，实现了PLRC－FDTD 方法的并行化计算，并行计算的结果与CST 仿真结果吻合，具有较高的数值精度，以及加速比和效率。因此，大幅提高了FDTD 方法针对色散介质的求解速度。

［1］ Kelly.Piecewise linear recursive convolution for dispersive media using FDTD［J］.IEEE Transactions on Antennas and Propagation，1996(6):792－796.

［2］ Taflove.Computational electrodynamics:the finite－difference time－domain method［M］.Boston:Artech House，2000.

［3］ 莫则尧，袁国兴.消息传递并行编程环境MPI［M］.北京:科学出版社，2011.

［4］ Anon.OpenMP application program interface，version2.5［EB/OL］.(2005－05－20)［2015－02－10］http://www.openmp.org.

［5］ 葛德彪.电磁波时域有限差分方法［M］.西安:西安电子科技大学出版社，2011.

［6］ 李正浩，周俊，遛达刚.基于OpenMP 的电磁场FDTD 并行程序性能分析［J］.现代电子技术，2008，31(5):135－136.

［7］ Li Jianjiang，Shu Jiwu，Chen Yongjian，et al.Analysis of factors affecting execution performance of openmp programs［J］.Tsinghua Science and Technology，2005，10(3):304－308.