基于小波和脊波变换的探地雷达信号杂波抑制

于海燕

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

探地雷达［1］(Ground Penetrating Radar，GPR)是利用电磁波探测地下目标，通过分析电磁信号与地下目标的相互作用，从而提取目标的性质、形状等信息。由于探地雷达工作对象及环境的特殊性，在接收到的探地雷达回波信号中，强背景杂波以及各种随机噪声对实际目标信号产生了较大的干扰，使得记录的探地回波剖面不能准确清晰地反映目标体，严重影响了探地雷达的目标检测能力。因此，如何有效地抑制背景杂波和随机噪声，成为探地雷达应用的一个重要研究课题。围绕如何消除强探地雷达背景杂波问题，研究者提出了多种通过去除直达波达到消除探地雷达回波信号噪声干扰的方法，如时间窗法、平均法、模型法、移动平均滤波法、中值滤波法以及小波变换法等。这些方法虽然都能在一定程度上削弱直达波对探地雷达目标信号的影响，但在实际应用中也都存在各自的不足，如常用的平均法，在去除直达波的同时，对目标信号也会有损伤，而且不能消除其中的随机噪声。

小波在表示具有点奇异性的图像时能达到最优逼近，但不能充分利用图像本身的几何特征，即不是最优的函数表示方法［2－3］。为解决二维或更高维奇异性，斯坦福大学的Candes E.J.和Donoho D.J.提出了一种新的分析工具:脊波变换(Ridgelet Transform)［4］。Ridgelet 变换克服了小波变换在高尺度空间的缺点，能有效地描述沿直线或超平面的奇异性。本文结合小波和脊波的特点，将其应用到探地雷达信号处理中，去除探地信号的随机噪声以及直达波，并通过实测数据仿真验证算法效果。

1 小波变换与脊波变换

设Ψ(t)∈L2(R)，其Fourier 变换记为)。当Ψ(ω)满足可允许条件

则称Ψ(t)为基本小波或小波母函数［2－3］。

设f(t)∈L2(R)，Ψ(t)是一个基本小波，令

其中，a，b∈R，a≠0，则称函数Ψab(t)为小波母函数Ψ(t)生成的依赖于参数a，b 的连续小波，a 为尺度因子;b 为平移因子。

对于任意f(t)∈L2(R)，其连续小波变换为

脊波变换通过Radon 变换将奇异线投影成奇异点，利用小波检测其中奇异点，然后利用逆Radon 变换将奇异点影射成奇异线［3－4］。

假设f(x)是一个双变量可积的函数，则其在R2上的二维连续Ridgelet 变换(2D Continuous Ridgelet Transform)定义为

对于每个a ＞0，b∈R，θ∈［0，2π)，可定义Ridgelet 函数为

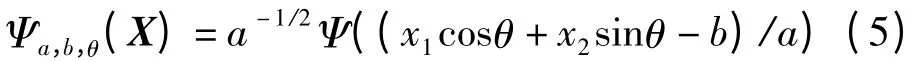
其中，a 是尺度因子;b 是平移因子，且X=(x1，x2)T。函数Ψa，b，θ(X):R2→R2沿着直线x1cosθ+x2sinθ－b=const 是一个常值，横向截面为一小波函数的Ψa，b(t)=a－1/2Ψ((t－b)/a)，故称为脊波。从脊波变换的结果重建原函数可通过如下公式完成

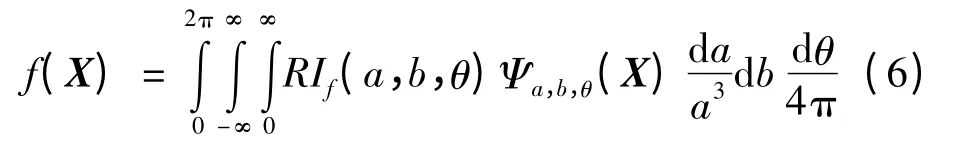
脊波变换和小波变换可通过Radon 变换联系在一起。f(x)的Radon 变换可写为

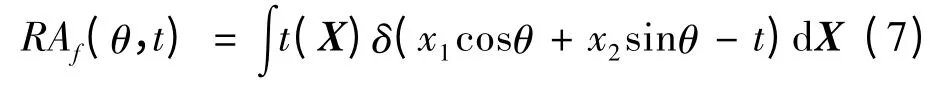
由式(7)可见，f(x)的Radon 变换是f(x)沿不同θ 的积分(投影):而f(x)的脊波变换可在f(x)的Radon 变换的基础上，沿着每个积分方向作一维小波变换得到，即

而重建原函数可通过对脊波变换的结果沿每一方向作一维小波逆变换，然后进行反Radon 变换得到。因此，脊波变换可以通过Radon 变换和一维小波变换间接地来实现［5］。

有限Ridgelet 变 换［6］(Finite Ridgelet Transform，FRIT)是在FRAT 变换的基础上经一维小波变换得到的。一个p×p(p 要求是一个素数)大小的图像f(i，j)，其中i，j∈{0，1，2，…，p－1}。其的FRAT 变换定义为

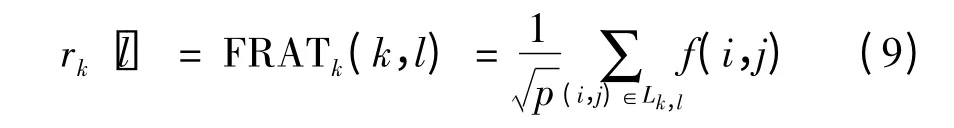
其中，k∈{0，1，2，…，p}，l∈{0，1，2，…，p－1}，而Lk，l是落在满足斜率k 和截距l 的直线上图像象素点的集合，其具体定义如下

式中，表示的是求余运算，以保证j 落在{0，1，2，…，p－1}范围内。由式(9)可知，FRAT 变换是满足要求的直线上的图像象素点灰度值的累加求和，而满足要求的直线则由式(10)定义。一个p×p 大小的图像经FRAT 变换后，将得到(p+1)×p 大小的矩阵，其有p+1 个斜率方向，每个方向上有p 个系数。

得到FRAT 变换的结果后可通过下式的FBP(Finite Back Projection)反变换来重建原图像

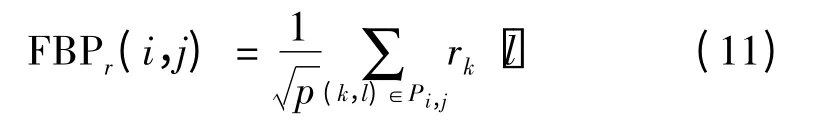
其中，Pi，j指的是所有通过点(i，j)的直线的斜率k 和截距l 的集合，即

其中，k∈{0，1，2，…，p－1}…∪{(k，l):l=i，k=p}，由式(9)和式(11)所定义的FRAT 变换和FBP 变换要求变换的图像均值为零，对于均值不为零的图像可以在变换前先减去均值，以保证变换前的图像均值为零;反变换回来后再加上图像均值即可恢复原图像。

对于p×p 大小的图像经FRAT 变换后，得到p+1个(投影)方向，沿每一方向做一维的小波变换即可得到FRIT 变换。而反变换IFRIT(Inverse Finite Ridgelet Transform)可通过FRIT 变换的结果沿每一方向作一维小波逆变换，再经FBP 变换得到［7－8］。

2 探地雷达信号

探地雷达［1］工作时，在雷达主机控制下，脉冲源产生周期性的毫微秒信号，并直接馈给发射天线，经由发射天线耦合到地下的信号在传播路径上遇到介质的非均匀体(面)时，产生了反射信号。接收信号由4 个部分组成:天线串扰，地面反射，目标反射以及白噪声。如图1 所示，接收信号可公式化为:w=s+c+n+b。s 是目标反射的信号，是真正需要的信号。c 是发射天线和接收天线之间的串扰信号。对于这个干扰信号可以通过天线校正或者在发射天线和接收天线之间加屏蔽隔板进行消除。n 是噪声项，由测量噪声和模型噪声组成，可假定它是一个加性高斯白噪声。b 是地面反射信号及地下各种杂质干扰带来的噪声信号。由于天线和地面之间的阻抗不匹配，从而引起电磁波的多次反射，又被称为直达波，其是探地雷达方法的主要干扰之一。地面的第一次反射信号最强，以后逐渐衰减。对于探测浅地层的探地雷达来说，这种多次反射造成的影响较大，地下各种杂质带来的干扰统称为背景噪声，都是在杂波抑制中需要去除的信号。

图1 探地雷达信号模型

3 自适应阈值去噪

利用小波和脊波变换去除探地雷达信号的白噪声n，信号和噪声在小波域中具有不同的性态表现，其小波系数幅值随尺度的变化趋势不同，随着尺度的增加，噪声系数的幅值较快衰减为零，而真实信号的幅值基本保持不变。因此，可通过设定阈值的方法在小波域去除噪声［9－10］。设观察到的是迭加了噪声后的数据，f［i，j］为原始图像，g［i，j］为加噪图像，模型如下

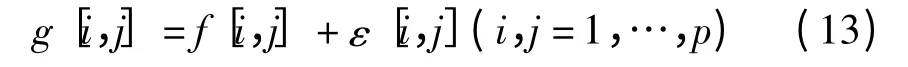
其中，{ε［i，j］}是服从N(0，σ2)分布的高斯白噪声，其是独立的均匀分布。

(1)软阈值操作

其中，t 为阈值;Yk为噪声图像对应的小波系数;Y'k为阈值处理后的小波系数;sgn(Yk)为元素Yk的符号。

(2)确定阈值的方法。利用BayesShrink 降噪算法［9－10］分别确定不同尺度下的阈值:TB=σ2/σx。其中，σ 噪声的标准偏差，σx为某尺度下小波系数的标准偏差。

经过脊波变换后得到的系数可分成两类:第一类仅由噪声变换后得到，这类系数幅值小，并随着尺度的增加，系数的幅值也相应减小;第二类主要由信号，特别是图像的直线奇性特征变换而来，这类系数幅值大。同样可通过BayesShrink 降噪算法对各尺度下的Ridgelet 系数进行软阈值操作，去除噪声，并有效地保留图像的直线奇异特征。

根据上述理论知识，文献［11］的方法对探地雷达信号的噪声进行如下处理:首先，对含噪图像分别进行脊波变换和小波变换，并对脊波域和小波域系数分别进行软阈值化，处理式(14);其次，对处理后的脊波系数和小波系数进行逆变换。设R(i，j)为脊波重构图像;W(i，j)为小波重构图像;H(i，j)为最终重构图像。对重构图像进行线性组合:H(i，j)=βR(i，j)+(1－β)W(i，j)，其中，β 为调节参数，0≤β≤1。

4 脊波变换去除直达波

直达波是直接耦合并经过地表传到接收端，相对于目标的散射信号具有更大的幅度。如果直达波与目标散射信号在时间上能够分离，则可借时间划分来判定目标。当目标离地表距离较大时，直达波与目标回波信号在时间上是分开的，则直达波对目标的估计影响较小;而当目标离地表较近时，目标回波信号叠加在直达波上，则直达波就对信号形成严重干扰，从而严重影响目标的探测。如果不能较好地去除直达波，目标将无法识别。由于回波信号电平很低，检测困难，例如对浅层埋设的塑料地雷的探测，所以抑制直达波是探地雷达的关键步骤。

图像的脊波变换是通过对Radon 域内的切片进行一维小波变换而得到的，而图像的Radon 变换就是将原始图像变换为其在各个方向上的投影。由于地面是水平的，其反射波即直达波信号的大小随着垂直距离变化，所以直达波在水平方向大小一致，因此在探地雷达信号的成像图中呈现的是一条水平线，而目标反射波形式为一个双曲线的波形。本文利用脊波变换的方向敏感性，将探地信号进行脊波变换，并将水平方向的向量系数{FRITg［k，l］，k=p}置零，即去除变换后雷达成像图在水平方向上的投影，从而去除直达波，同时又保留目标的反射信号，最后得到清晰的目标反射波形。

5 实验结果

文中实验数据为256×70 大小、含有噪声的雷达成像图，埋藏目标是1 个圆盘。如图2 所示，其中直达波信号较强，而目标反射信号显示不明显。

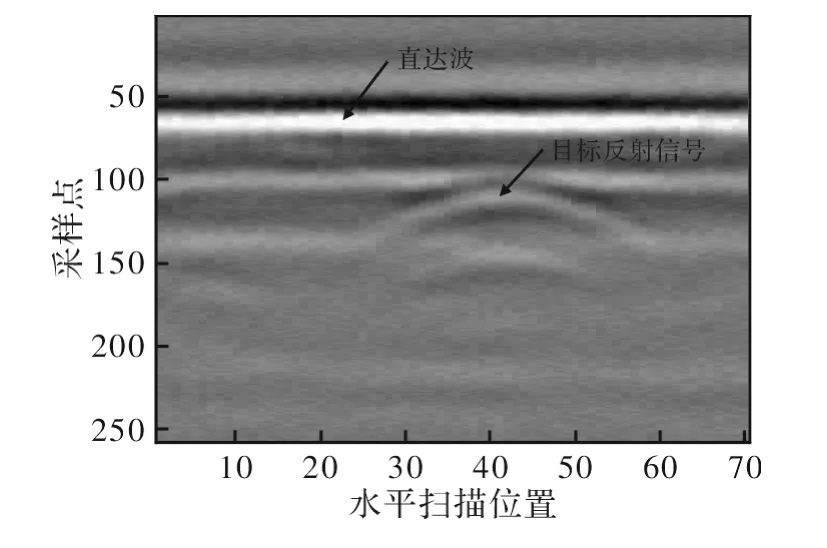
图2 原始雷达成像图

(1)用小波和脊波进行自适应软阈值去噪。图3是经过小波和脊波去噪得到的成像图，其中β=0.5。对比图2 和图3，可明显看出去噪后的雷达成像图变得更加平滑;特别是噪声污染后的直达波信号得到了较好的恢复，这主要是因为小波能有效地处理二维空间中具有点奇异性的信号，脊波能有效地处理二维空间中具有直线奇异性的信号，由小波去噪和脊波去噪后的合成图像H(i，j)能够较好地保持雷达信号的线奇异性和点奇异性特征。

图3 经小波和脊波阈值去噪后的成像图

(2)去除直达波。图4 是成像图第42 列的信号波形对比图，data1 为原始信号波形，data2 为去除直达波信号的波形图，从中可看出直达波信号大部分被去除。对比原始的成像图和去除直达波的效果图，如图2 和图5 所示，直达波被有效地去除，目标体反射信号灰度加强，目标体反射形成的曲线带更为清晰，背景噪声得到了有效抑制。

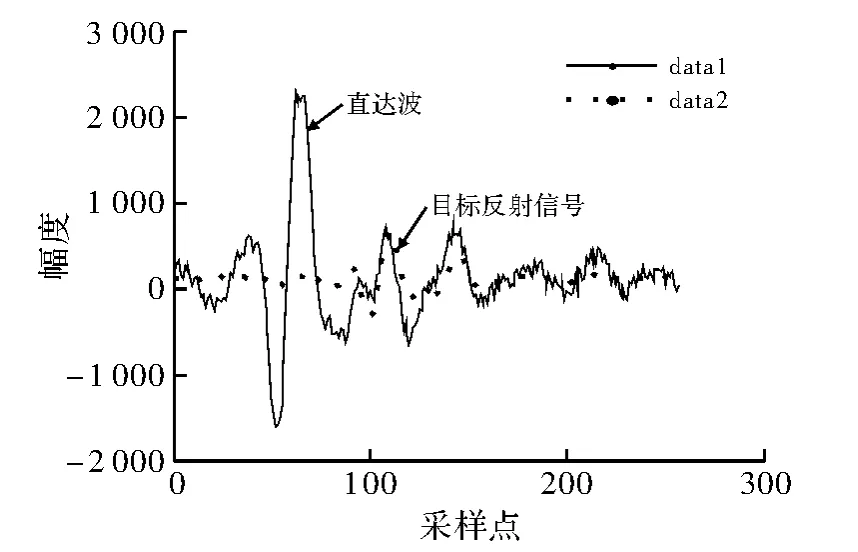
图4 去直达波前后的波形对比

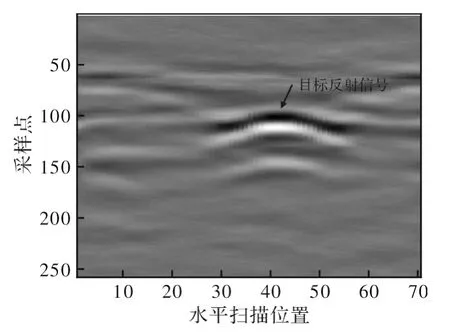
图5 去直达波后的成像图

6 结束语

探地雷达信号处理的目的是压制随机的和规则的干扰波，以最大可能的分辨率来显示目标反射波，便于提取各种有用参数，从而对探地回波剖面进行准确合理的地质解释。本文结合小波变换和脊波变换各自优势，将其应用于探地雷达信号进行处理，既可消除高斯白噪声，又可消除直达波，使目标体反射图像更为清晰，且易于实现。

［1］ 陈文超，师振盛，汪文秉，等.小波变换在去除探地雷达信号直达波的应用［J］.电科科学学报，2000，15(3):352－357.

［2］ Donoho D L.Ridgelet function and orthonormal ridgelets［J］.Journal of Approximation Theory，2001，111(2):143－179.

［3］ 杨鑫蕊.改进的小波阈值去噪算法研究［D］.哈尔滨:哈尔滨理工大学，2014.

［4］ Candes E，Donoho D L.Ridgelets:a key to higher－dimensional intermittency?［J］.Philosophical Transactions of the Royal Society of London，1999，357(1760):2495－2509.

［5］ 侯彪，刘芳，焦李成.基于脊波变换的直线特征检测［J］.中国科学:E 辑，2003，33(1):65－73.

［6］ Do M N，Vetterli M.Orthonormal finite ridgelet transform for image compression［J］.IEEE Image Processing(ICIP)，2000，27(2):367－370.

［7］ 李应岐，何明一.一种基于近似有限Ridgelet 变换的SAR 图像分割方法［J］.计算机工程与应用，2005，41(9):13－15.

［8］ 李美丽.改进的基于脊波变换的图像去噪新算法［J］.计算机测量与控制，2012，20(6):1646－1652.

［9］ 高文仲，陈志云，曾秋梅.小波阈值图像去噪算法改进［J］.华东师范大学学报:自然科学版，2013(6):83－92.

［10］段永刚，马立元，李永军，等.基于小波分析的改进软阈值去噪算法［J］.科学技术与工程，2010，10(23):5755－5758.

［11］李根强，黄永东，蒋肖.基于小波变换和脊波变换的自适应图像去噪算法［J］.计算机应用研究，2012，29(8):3192－3194.