多特征组合及优化SVM 的电能质量扰动识别

韩 刚，张建文，禇 鑫，周贤姣

（中国矿业大学信息与电气工程学院，徐州221116）

电网中的非线性、冲击性和不平衡负荷的投入导致电网电压波形发生畸变、电压波动和三相不平衡等，造成严重的电能质量问题。深入研究影响电能质量的各种因素，实现电能质量扰动的准确分类，为电能质量的改善和治理提供决策依据[1]。

迄今为止，国内外已有大量学者研究电能质量扰动分类问题[2-3]。电能质量扰动分类包括扰动特征提取和分类识别。诸如傅里叶变换、dq 变换、时频原子变换、小波变换、S 变换、希尔伯特黄变换HHT（Hilbert-Huang transform）等多种方法[4-5]。电能质量扰动信号分类主要有人工神经网络、专家系统、贝叶斯分类和支持向量机SVM 等方法[6]。SVM是一种基于统计学习理论的模式识别方法，在解决小样本、非线性及高维模式识别问题中具有独特优势，克服了人工神经网络易陷入局部最优解和训练时间长的缺点[7]。然而，核函数是影响SVM分类性能的关键，SVM 的惩罚因子和核参数的不同取值组合与预测精度有较大差别。最优参数组合决定了高维空间中线性分类的复杂程度，可减少特征计算量，实现实时分类。PSO 算法是一种基于群体和适应度的具有全局寻优能力的优化算法，可很好解决SVM 参数选择问题。

基于此，本文针对8 种常见的电能质量扰动及2 种复合扰动信号，采用小波变换和S 变换提取各扰动信号的特征向量；采用粒子群PSO 优化的SVM 进行分类识别。首先针对提取的小波能量谱中谐波信号的明显差异，通过设定特征阈值进行初步分类，然后结合S 变换提取的3 种特征，采用优化参数的SVM 对没有区分开来的扰动进行后续分类。仿真结果表明，提取的各扰动特征信息能有效用于优化参数的SVM 分类识别，相比未经优化的SVM 模型，基于PSO 算法优化的SVM 具有较高的识别精度和运算速度，且抗噪能力强，为电能质量监测的实际工程应用提供了依据。

1 小波变换与S 变换提取扰动特征

1.1 电能质量扰动信号仿真模型

针对短时电能质量变化和暂态扰动现象的不同特点，本文研究的电能质量扰动信号有：电压暂升（swell）、电压暂降（sag）、电压中断（interrupt）、谐波（harmonic）、电压闪变（flicker）、暂态振荡（transient oscillation）、含谐波的电压暂升（swell with harmonic）以及含谐波的电压暂降（sag with harmonic），如表1 所示[8]。表中A 为扰动的电压幅值，归一化值为1；β 为基频倍数；t1为扰动发生时刻；t2为扰动结束时刻；τ 为衰减时间；u（t）为单位阶跃函数；ω 为基波角频率，基波频率设定为50 Hz；T为周期。基于扰动信号的模型参数确定采样频率，本文采样频率为6 400 Hz，每个周期采样128 个点，共10 个周期，总采样1 280 个点，并对每个扰动信号叠加信噪比（SNR）为30 dB，以此为分析对象，运用小波变换和S 变换提取扰动信号的特征。

1.2 小波变换提取扰动特征

小波变换是基于频带的分析方法，更适于分析幅值随时间变化而频率分布相对稳定的暂态信号，所以小波系数和小波能量表征了信号在各频带的分布情况。仿真产生的8 种电能质量扰动信号和标准正弦信号，本文采用db4 小波分别对其进行10 层分解，为使暂态分量的主要频率成分尽量分布在小波频带的中心，从而减少频谱泄露。各分解层小波能量[9]为

式中：dj（k）为小波细节分量Dj单支重构后细节分量系数；j 为分解层层数；N 为细节分量系数个数。

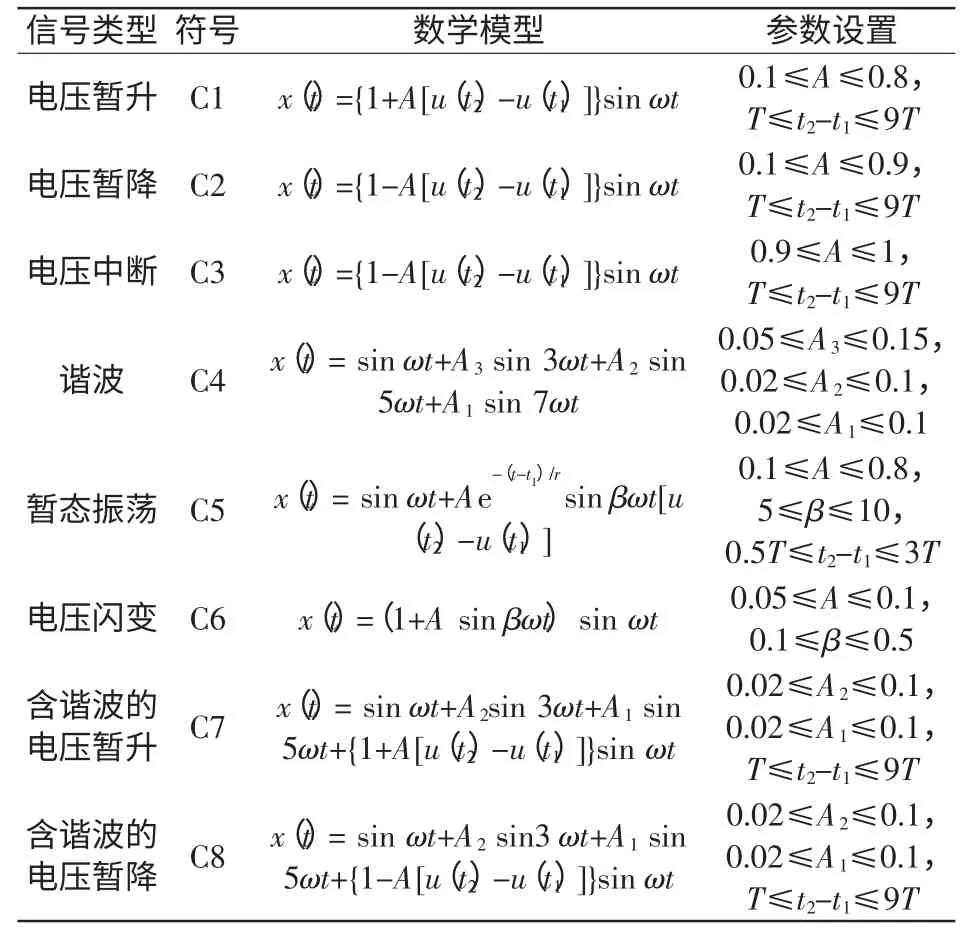
表1 电能质量扰动信号数学模型[8]Tab.1 Signal mathematic model of power quality disturbances

电能质量扰动信号各分解层的小波能量归一化值分布如图1 所示。

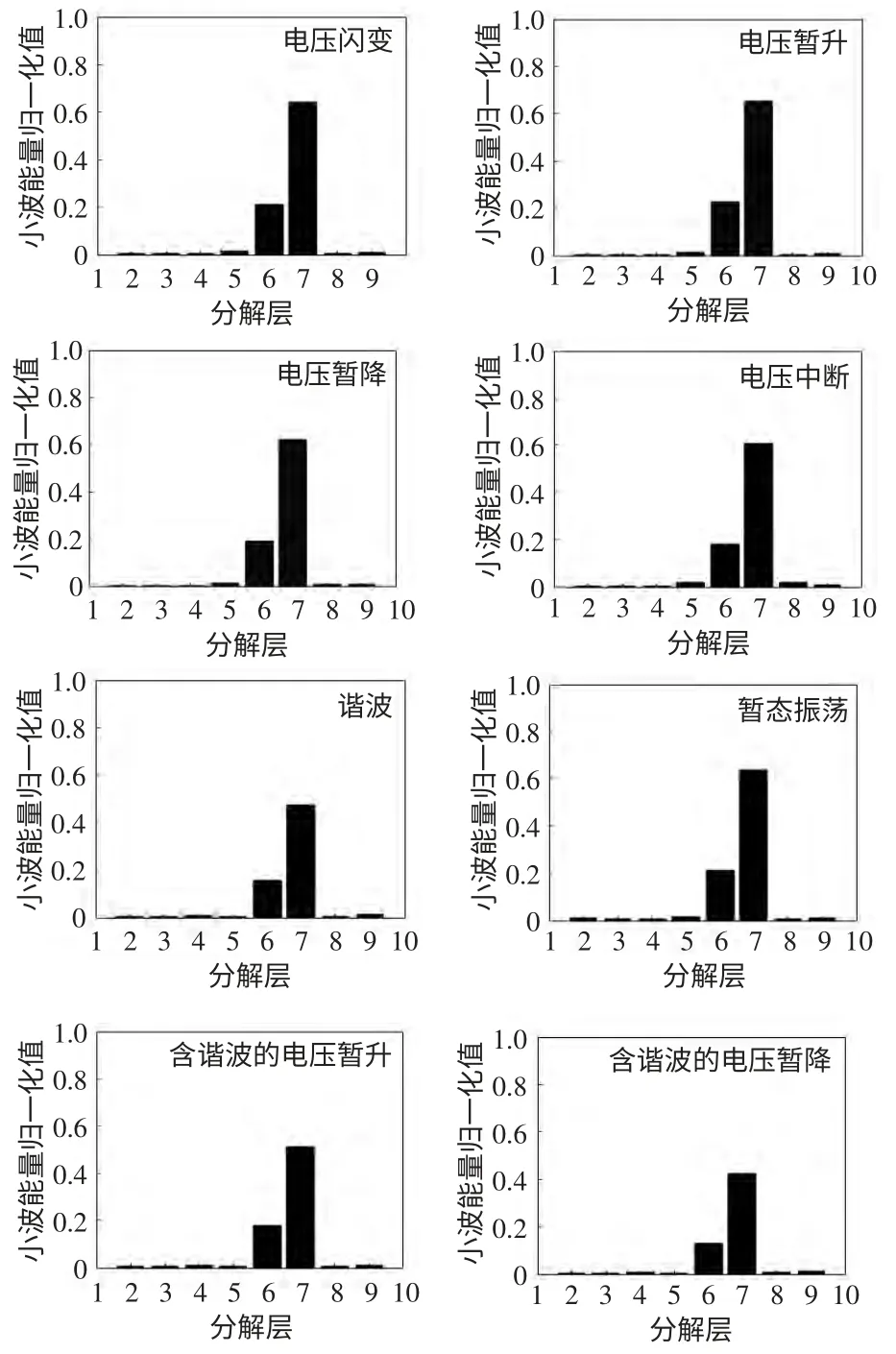
图1 电能质量扰动信号的小波能量分布Fig.1 Wavelet energy distribution of power quality disturbance signals

各扰动信号的小波能量主要分布在第7 分解层，在第6 层也有少量能量分布。各电能质量扰动的差异可由小波能量特性向量表征，因此可以作为其被识别的一个特征量。

由图1 可以看出，谐波以及含有谐波的电压暂升、暂降复合扰动信号的小波能量谱中，第6、7层的能量值明显较低，可以很容易地与其他几种扰动类型区分开来。以8 种电能质量扰动分别叠加信噪比为30 dB 为例，每种扰动随机生成100 个样本进行测试，设定第7 层能量归一化阈值为0.600 0 时，识别精度高，误差较小。

1.3 S 变换提取扰动特征

S 变换的高斯窗的高度和宽度随频率变化，它既有小波变换多分辨率分析的特点，又有短时傅里叶变换单频率独立分析的能力，同时避免了二者窗函数选择的问题[10]。电能质量扰动信号经过S 变换后得到一个复时频矩阵，对其取模可得S 模矩阵，表示为Sa[l，f]。其中，行向量代表某一频率处幅值随时间变化情况，列向量代表某一时间点幅频特性。仿真产生的8 种电能质量扰动信号和标准正弦信号，对其进行S 变换分析。基于各扰动信号在时间、幅值和频率处的差异性，本文提取如下特征：

（1）基频幅值特征提取[11]。定义S 变换模时频矩阵中对应的最大幅值随时间变化的基频曲线Vfb（l），则其表达式为

式中：l 为采样时刻；fb为基波频率。

S 变换的基频幅值特征为

后续分类中，以电压暂升、电压暂降、电压中断、电压闪变、暂态振荡及标准正弦信号为例，提取基频幅值特征Fam。仿真信号分别叠加信噪比为30 dB，每种扰动随机生成100 个样本，则幅值特征如表2 所示。

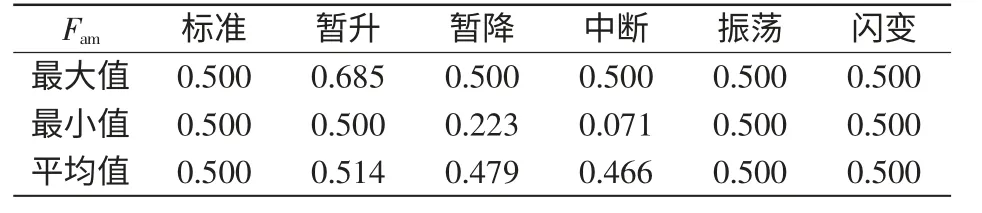
表2 S 变换的基频幅值特征值Tab.2 Eigenvalues of amplitude of basic frequency for S-transform

由表2 可知，电压暂升、电压暂降、电压中断的基频幅值特征具有明显差异，可以通过设定阈值将这3 种扰动与其他区分。同时，仿真分析发现，对于含谐波的暂升、暂降扰动，谐波成分并不影响基频变化，因此，也可以用幅值特征进行识别。

（2）幅频标准差特征提取。电压暂升、暂降、中断，闪变基频幅值变化较大，而暂态振荡、谐波基频变化幅值较小，因此，频率对应幅值的标准差曲线能够区分上述几种扰动。定义S 变换模时频矩阵中频率对应幅值标准差曲线Vs（f），其表达式为

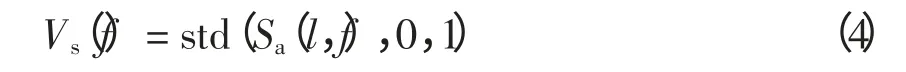
式中，f 为对应频率。

（3）高频段幅频特征提取。以100 Hz 以上频率范围为高频段，定义S 变换模时频矩阵中频率对应的最大幅值曲线Vam（fh），其表达式为

式中，fh为高频段频率。

S 变换的高频段幅频特征为

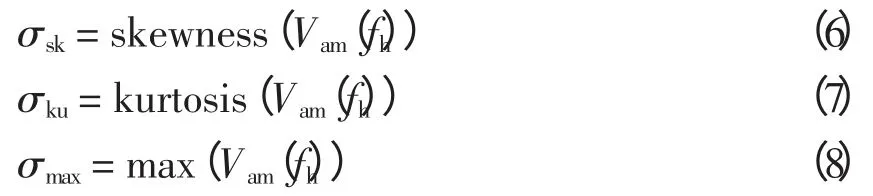
式中：σsk、σku分别为高频段幅频曲线的偏度和峭度；σmax为高频段幅频曲线的最大值。以各扰动信号分别叠加信噪比为30 dB 为例，每种扰动随机生成100 个样本，提取高频段幅频特征量Vam，如表3所示。

表3 S 变换的高频段幅频特征值Tab.3 Eigen values of amplitude of high frequency for Stransform

可以看到，S 变换模时频矩阵中频率对应的最大幅值曲线中电压闪变、谐波偏度值和最小值变化明显，电压暂升、闪变的峭度值变化明显，因此可以通过设定阈值将其识别。

1.4 多特征组合

当电能质量扰动类型较多时，单纯采用某一种特征难以构建合适的规则来区分所有的扰动类型，而将上述提取特征量组合生成组合特征，能够使各个单项特征之间特性互补，取得较好的分类识别效果。

各扰动信号的小波能量谱特征向量中，通过设定合适阈值可以初步将谐波、含谐波的暂降和含谐波的暂升与其他5 种扰动区分开来。后续分类中S 变换提取的3 个特征，其中：基频幅值特征Fam可以将暂态振荡和电压闪变与电压暂升、暂降和中断区分开来；幅频标准差特征Vam可以将暂态振荡与其他4 种扰动区分开来；高频段幅频特征可以暂升与闪变区分开来。

2 粒子群优化支持向量机的电能质量扰动信号识别

2.1 支持向量机

支持向量机SVM（support vector machine）是解决小样本数据的分类和回归问题下的学习算法，其主要思想是，将输入空间中线性不可分的样本经过非线性映射到高维空间，变成线性可分问题。通过建立一个超平面，使正反样本之间的隔离边缘最大化[12]。

定义分类平面

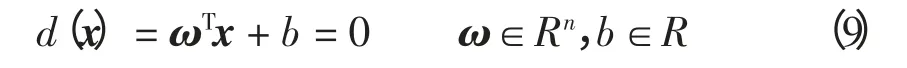
该分类平面能够将线性可分训练样本集（x1，y1），…，（xn，yn），x∈Rn，y∈{+1，-1}准确分开，并且使正反样本之间的隔离边缘最大化，则得到超平面为

正反样本距分类超平面的距离，即分类间隔为

因此，构建最优分类超平面就转化为求解分类间隔最大问题，即‖ω0‖最小化为

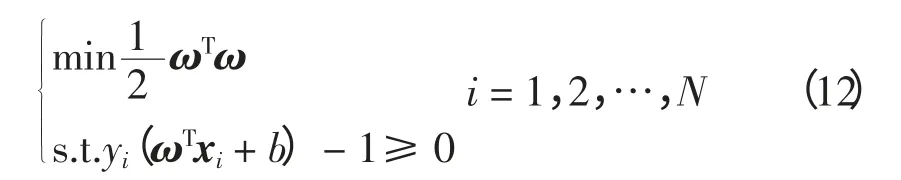
利用不等式约束条件极值方法求解，有

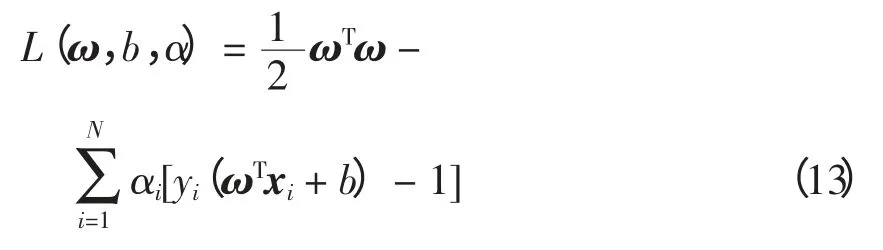
式中，αi≥0 为Lagrange 乘子，通过对ω、b 求偏导求其最小值，并把问题转化为对偶问题

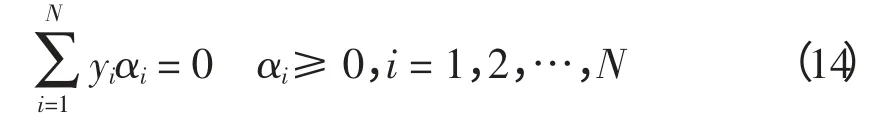
约束下对αi求解下列函数最大值：

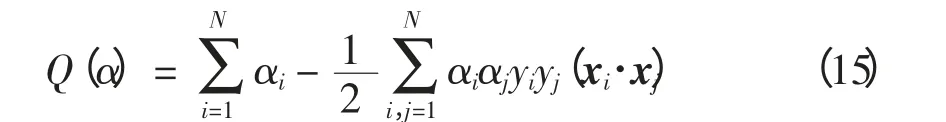
综上所述，可以得到最优分类函数为

式中：sgn（）为符号函数；b*为分类阈值。充分利用核函数K（xi，xj）代替特征空间中内积（xi，xj），把在高维空间中求取最优超平面问题转化到原始空间中进行。此时，最优目标分类函数变为

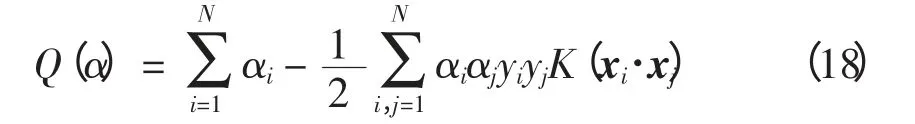
核分类函数表示为

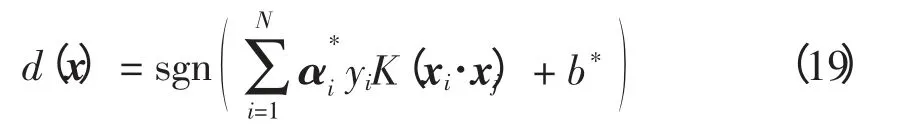
而在线性不可分时，支持向量机通过引入松弛变量ζi和惩罚因子C，则目标函数表示为

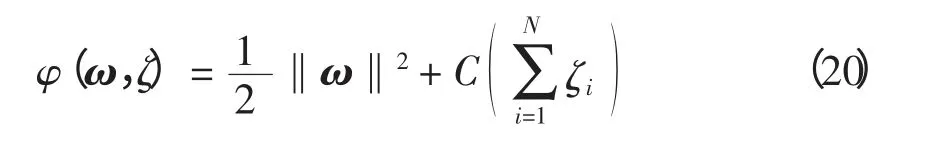
2.2 核函数选取

SVM 是一种以统计学习理论为基础的学习算法，核函数及核参数的选择对SVM 的性能具有决定作用。选择不同的核函数会产生不同的SVM 算法。常用的核函数有：多项式核函数、多二次曲面核函数、Sigmoid 感知核函数和高斯径向基RBF（radial basis function）核函数。由于RBF 核函数能有效处理非线性分类问题，因此，本文选定RBF 核函数，其表达式为

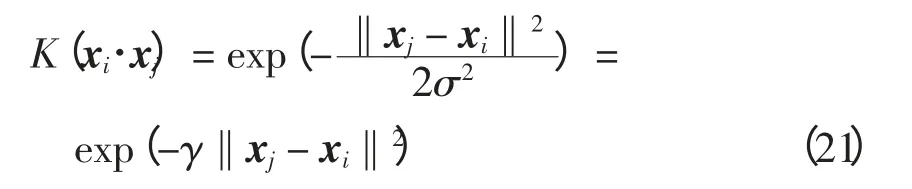
式中，γ 为核函数的参数。

在选定RBF 作为核函数后，SVM 模型需要选择的参数有：超参数γ 和核参数σ2。其中，γ 对应向量机中的惩罚因子C，其决定训练误差的大小和泛化能力的强弱；核参数σ2影响样本数据在特征空间的分布复杂度和支持向量之间的相关程度。

2.3 基于粒子群算法的参数优化

核函数是影响SVM 分类性能的关键，核参数的选择和寻找最优参数（C，γ）组合的方法尤为重要，决定高维空间中线性分类的复杂程度，降低特征向量维数，提高分类的实时性。粒子群算法是一种基于群体和适应度的具有全局寻优能力的优化算法[13]。在SVM 模型参数寻优过程中，寻优搜索空间中的可能解（C，γ）被称为一个“粒子”，所有粒子都被赋予位置和速度两个特征，并且存在一个被优化函数决定的适应值。粒子群算法初始化为一群随机粒子，粒子通过跟踪两个极值寻找最优解：第一个为粒子本身所找到的最优解，称为个体极值；另一个极值是整个种群找到的最优解，称为全局极值。本文通过粒子群算法对SVM 参数最优解进行搜索，从而获得优化的SVM 分类模型。本文分别选取每个粒子k 折交叉验证准确分类率和均方误差作为粒子群算法的适应度函数，其表达式分别为

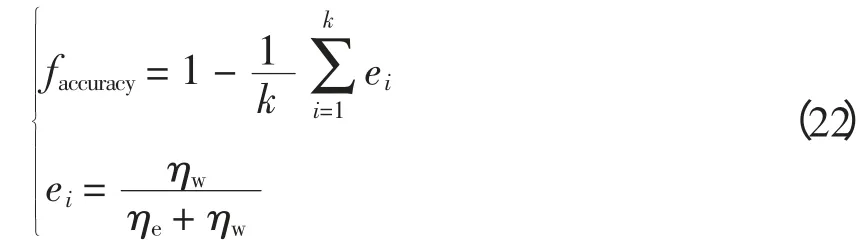
式中：ei为第i 次交叉验证错误分类率；ηe为正确分类样本数；ηw为错误分类样本数；因此faccuracy值越大，则分类模型准确率越高，支持向量机分类效果越好。

式中：n 为训练样本个数；yi为实际值；yi′为预测值。

本文采用粒子群算法对SVM 模型参数进行优化，寻找最优的参数组合（C，γ）。其具体优化步骤如下：

（1）初始化粒子种群和模型参数的搜索范围，即设定迭代次数、粒子维数、种群规模、速度范围、初始适应值，随机产生1 组（C，γ）参数作为初始解空间；

（2）用粒子（C，γ）对应的优化SVM 模型对测试样本进行预测，并统计其适应值，采用式（21）～（22）进行适应度评估；

（3）对每个粒子（C，γ），比较其经历过的最好的个体极值的适应度值和群体全局极值的适应度值，若比初始设定的效果好，则更新，否则保持原来的数据；

（4）整个群体粒子计算后，判断是否满足终止条件，若不满足，则粒子依照式（22）、（23）更新，产生新的粒子群，重复步骤（2），若满足最大迭代次数，计算结束并输出结果。

3 实验仿真与分析

3.1 仿真参数寻优及测试结果

在表1 提供的电能质量扰动信号模型的基础上产生样本数据。本文采用Matlab 仿真产生扰动信号样本，其基波频率为50 Hz，采样频率为6 400 Hz，即每周波采样128 个点。为接近实际情况，每种扰动信号终止时间、幅值、持续时间等参数在允许范围内随机变化。在实际电网中，扰动信号总受到不同程度的噪声影响，因此，所有扰动信号均叠加信噪比为30 dB 的高斯白噪声。提取上述8 种类型扰动信号及标准正弦信号各提取100 组特征向量，各类信号中50 组数据作为训练集，其余50 组作为测试集。采用第2.3 节的基于粒子群算法的SVM参数寻优方法优化最优参数组合（C，γ），将测试数据集输入最优模型进行测试。

仿真实验中，SVM 惩罚因子C 参数的变化范围为[0.1，100]，γ 参数的变化范围为[0.01，1 000]，最大进化迭代数为100，种群数量为20，粒子群参数局部搜索能力、全局搜索能力和惯性权重等参数设置采用文献[14]中的方法。

整个SVM 参数寻优过程中，采用式（22）准确分类率适应度函数和式（23）均方误差适应度函数作为评价标准，如图2 所示。从图2（a）的准确分类率适应度值可以看出，整个寻优过程中，最佳适应度值为98.88，平均适应度值在第16 代时找到最佳适应度值，之后最佳适应值一直保持平稳。从图2（b）所示的均方误差适应度值可以看出，最佳适应度值为0.018 2，同样，平均适应度值在第16 代时找到最佳适应度值，之后最佳适应值一直保持平稳。最终确定最优参数组合C = 13.329 9，γ =4.710 1，将测试数据集输入到优化参数的SVM 中进行分类。

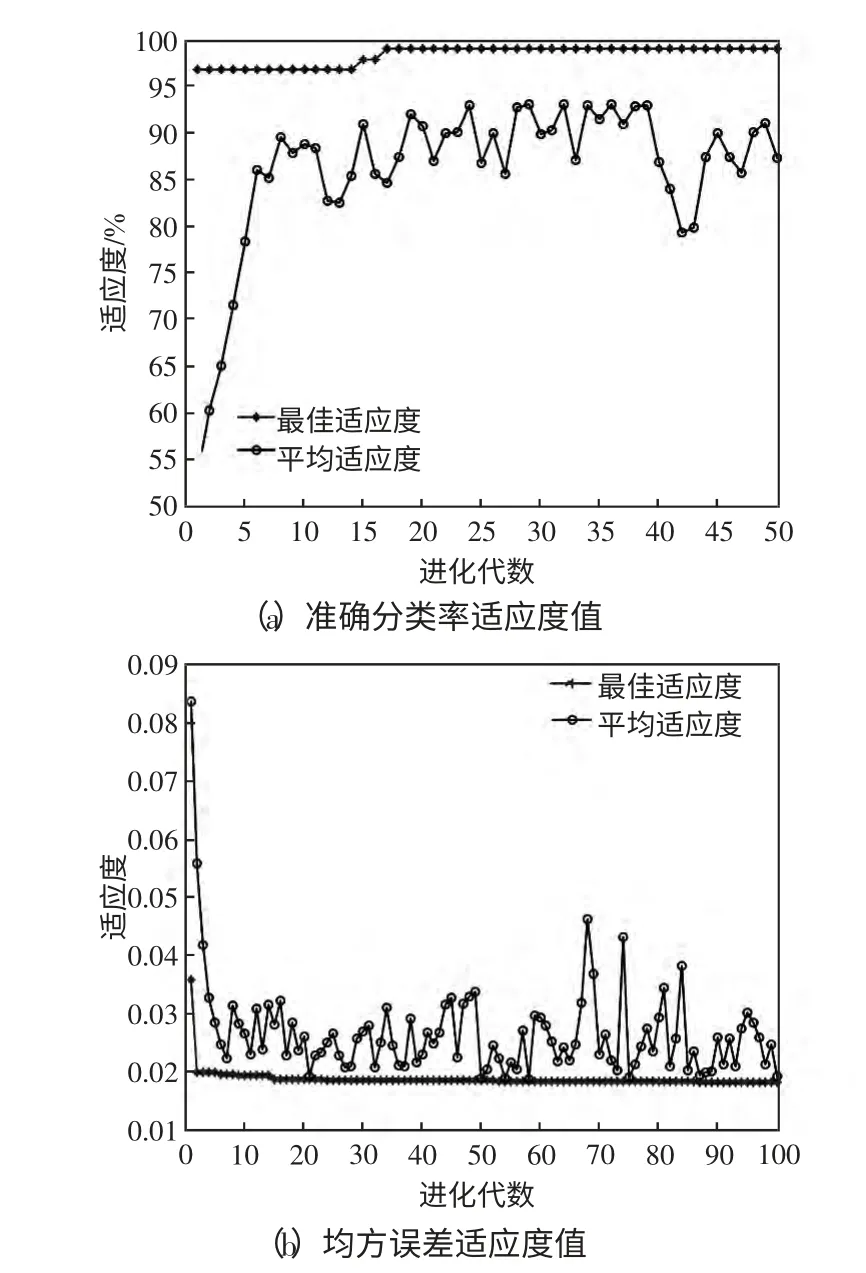
图2 粒子群算法寻优参数Fig.2 Optimal parameters of PSO

3.2 测试结果分析

结合第3.1 节优化参数的SVM 测试模型，将50 组特征向量作为测试集，用于优化参数的SVM 模型进行分类，测试结果如表4 所示。从表4 中可以看出，相比于未经优化的SVM 模型，基于粒子群优化的SVM 识别精度高，所需分类时间少，充分表明基于粒子群算法优化参数的SVM 模型的有效性。

表4 测试样本的识别结果Tab.4 Identification result of testing samples

为了进一步验证本文特征提取方法和粒子群优化支持向量机模型的稳定性和抗噪能力，每种电能质量扰动信号分别叠加信噪比为50 dB、40 dB、30 dB、20 dB 高斯白噪声，各提取50 组特征向量作为测试集，识别结果如表5 所示。从表5 可以看出，基于粒子群优化的SVM 识别精度高，抗噪能力强。

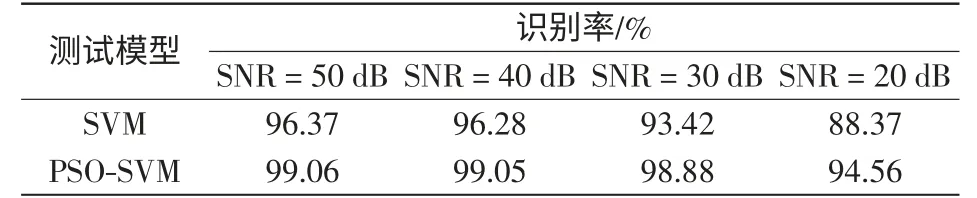
表5 不同信噪比识别结果对比Tab.5 Comparison of results of different SNR

4 结论

本文提出一种基于多特征组合及粒子群优化的支持向量机（SVM）的电能质量扰动识别方法。该方法采用小波变换和S 变换提取各扰动信号特征向量；采用粒子群（PSO）优化的支持向量机进行分类识别，仿真测试结果表明：

（1）针对提取的小波能量谱中谐波信号的明显差异，通过设定特征阈值进行初步分类，然后结合S 变换提取的3 种特征，采用粒子群优化的SVM进行后续分类，仿真结果表明，提取的各扰动特征信息能够有效的用于优化参数的支持向量机分类识别。

（2）将粒子群算法用于支持向量机SVM 模型参数优化，具有较高识别精度和运算速度，并具备抗噪性。

本文的算例是基于Matlab 仿真平台完成的，进一步的研究将尝试其应用于实际的电能质量扰动分类测试，并将纳入更多的电能质量扰动类型，使分类方法更具普适性。

[1]张杨，刘志刚（Zhang Yang，Liu Zhigang）.一种基于时频域多特征量的电能质量混合扰动分类新方法（A new method for power quality mixed disturbance classification based on time-frequency domain multiple features）[J]. 中国电机工程学报（Proceedings of the CSEE），2012，32（34）：83-90.

[2]Karthikeyan M，Malathi V.Wavelet support vector machine approach for classification of power quality disturbances[J].International Journal of Recent Trends in Engineering，2009，1（3）：290-293.

[3]何朝辉，黄纯，刘斌，等（He Zhaohui，Huang Chun，Liu Bin，et al）.基于小波系数KPCA 和PNN 的电能质量扰动分类（Power quality disturbances classification based on kernel principal component analysis of wavelet coefficients and probabilistic neural networks）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（2）：76-81，108.

[4]王晶，沈月月，翁国庆，等（Wang Jing，Shen Yueyue，Weng Guoqing，et al）.广义S 变换在电能质量扰动识别中的应用（Application of generalized S-transform in power quality disturbances analysis）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（6）：57-61.

[5]黄奂，吴杰康（Huang Huan，Wu Jiekang）.基于经验模态分解的电能质量扰动信号定位方法（A method to locate power quality disturbing signal based on empirical mode decomposition）[J].电网技术（Power System Technology），2010，34（5）：41-45.

[6]秦业，袁海文，袁海斌，等（Qin Ye，Yuan Haiwen，Yuan Haibin，et al）.基于优化最小二乘支持向量机的电能质量扰动分类（Classification of power quality disturbances basedon optimized leastsquares supportvector machine）[J].电工技术学报（Transactions of China Electrotechnical Society），2012，27（8）：209-214.

[7]张俊才，张静（Zhang Juncai，Zhang Jing）.使用粒子群算法进行特征选择及对支持向量机参数的优化（Use PSO to perform feature selection and parameter optimization of SVM）[J].微电子学与计算机（Microelectronics&Computer），2012，29（7）：138-141.

[8]黄南天，徐殿国，刘晓胜（Huang Nantian，Xu Dianguo，Liu Xiaosheng）. 基于S 变换与SVM 的电能质量复合扰动识别（Identification of power quality complex disturbances based on S-transform and SVM）[J].电工技术学报（Transactions of China Electrotechnical Society），2011，26（10）：23-30.

[9]黄艳玲，司马文霞，杨庆，等（Huang Yanling，Sima Wenxia，Yang Qing，et al）.电力系统实测过电压信号的特征量提取与验证（Features extraction and validation from measured overvoltage signal of power system）[J]. 高电压技术（High Voltage Engineering），2013，39（1）：60-66.

[10]全惠敏，戴瑜兴（Quan Huimin，Dai Yuxing）. 基于S 变换模矩阵的电能质量扰动信号检测与定位（Detection and localization of power quality disturbances based on S transform module matrixes）[J].电工技术学报（Transactions of China Electrotechnical Society），2007，22（8）：119-125.

[11]陈华丰，张葛祥（Chen Huafeng，Zhang Gexiang）.基于决策树和支持向量机的电能质量扰动识别（Power quality disturbance identification using decision tree and support vector machine）[J].电网技术（Power System Technology），2013，37（5）：1272-1278.

[12]He H，Starzyk J A.A self-organizing learning array system for power quality classification based on wavelet transform[J].IEEE Trans on Power Delivery，2006，21（1）：286-295.

[13]唐发明，王仲东，陈绵云（Tang Faming，Wang Zhongdong，Chen Mianyun）. 支持向量机多类分类算法研究（On multiclass classification methods for support vector machines）[J].控制与决策（Control and Decision），2005，20（7）：746-749，754.

[14]李燕楠，包广清（Li Yannan，Bao Guangqing）.基于小波包和支持向量机的电能质量扰动识别（Power quality disturbance signals identification based on wavelet packet and SVM）[J].电力科学与工程（Electric Power Science and Engineering），2012，28（3）：21-26.