基于微分几何和扩张状态观测器的励磁控制

常鲜戎，张海生，崔赵俊

（华北电力大学电力工程系，保定 071003）

同步发电机励磁控制系统是现代电力系统的重要组成部分，对整个电力系统的稳定性有着重要作用。从PID 控制、电力系统稳定器到线性最优励磁控制，显著提高了系统电压和功角的稳定性。但设计所依据的是在电力系统某一特定状态下近似线性化的数学模型，在系统遭受大干扰、偏离设计平衡点较远时，控制效果就会减弱。近年来，非线性控制理论在电力系统得到大量研究[1-2]，很大程度上改善了系统大干扰的稳定性。但因电力系统模型及参数有不确定性，使得非线性励磁控制器在实际应用中有一定误差。

自抗扰控制技术[3]针对模型不精确和扰动等问题，提供一条新的解决思路。扩张状态观测器ESO（extended state observer）是其核心部分，在低阶情况下能有效观测系统的内外扰动，将此内外扰动的估计值补偿到控制规律中，以实现非线性模型动态补偿线性化[4]。文献[5]根据非线性控制系统的微分几何理论，提出非线性励磁控制器NEC（nonlinear excitation control）。虽然这种NEC 可显著改善电力系统的静态和暂态稳定性，但在稳定机端电压方面效果不是很理想[6]，而比例积分控制对机端电压具有良好的控制效果。

输出函数的选取会直接影响变换后的线性空间构成，从而影响控制器的最终控制效果[7-8]。文献[9]将输出函数选为发电机角速度的偏差，构造含有机端电压偏差ΔUt的伪线性系统，将ΔUt引入反馈，提高了机端电压的调节能力。变结构控制最大优点是滑动摸态对内部参数的变动和外部扰动作用具有不变性，或不灵敏性、自适应性[10]。

本文提出一种基于微分几何和扩张状态观测器的非线性变结构励磁控制。首先根据微分几何理论进行坐标变换，然后构造二阶的ESO 得到动态补偿线性化的系统，利用变结构理论设计虚拟控制量，并引入基于机端电压偏差的比例积分控制，从而实现非线性励磁控制规律的设计。

1 数学模型

对于单机无穷大系统，当同步发电机采用静止可控硅快速励磁方式时，发电机励磁控制系统数学模型可用非线性微分方程组描述为

式中：δ 为发电机功角；ω 为角速度；Eq′为q 轴暂态电势；H 为转动惯量；xd和分别为发电机直轴同步电抗和暂态电抗；Td0为发电机定子开路时励磁绕组时间常数；Td′为发电机定子闭路时励磁绕组时间常数为阻尼系数；Pm为发电机机械功率；Us为无穷大系统母线电压。

系统（1）化为仿射非线性系统，即

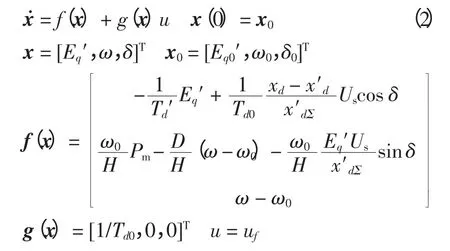
2 非线性励磁控制规律的设计

2.1 坐标变换

考虑到转速的变化超前于功角的变化和控制便于实现，同时也为了把输出函数的稳态值选取在新坐标系的原点上，将输出函数选为

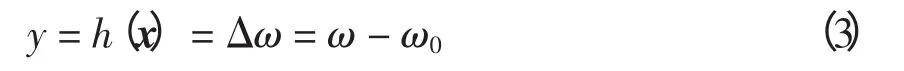
经计算可得：h（x）对系统的关系度为r=2。由于LgΔδ=0，故可选取以下坐标变换[11]，即

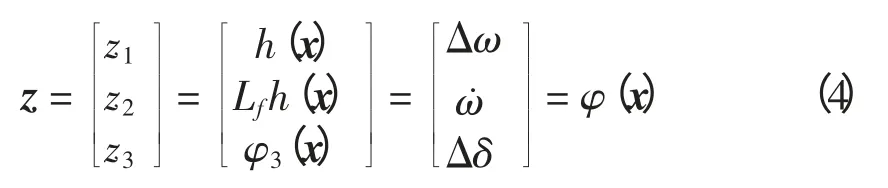
将式（1）变换成标准型方程为

根据微分几何理论，得

式中，w（x）为参数不确定造成的扰动。

可验证，φ（x）的雅可比矩阵是非奇异的，即

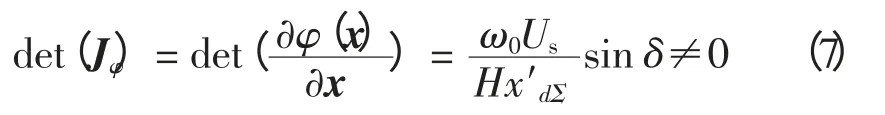
式（4）是状态空间[Eq′，ω，δ]T与[z1，z2，z3]T之间的一个局部微分同胚。

2.2 扩张状态观测器

ESO 利用非线性函数来设计比系统多一维的状态观测器，从而估计对象的各阶状态变量，对不确定模型和扰动实时作用量补偿。ESO 是动态过程，只需知道对象的输入和输出信息，对于系统构造ESO[4]为

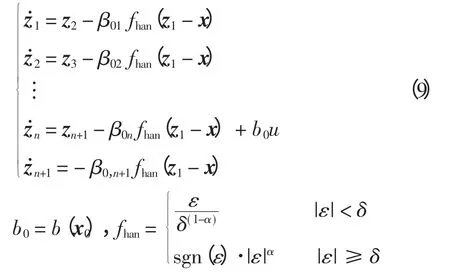
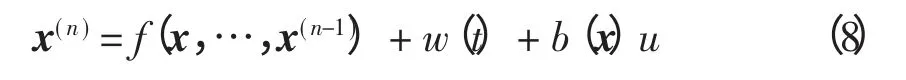
选择合适的增益系数β01，β02，…，β0，n+1，使ESO更好地跟踪系统的各个状态：z1→x，z2→x˙，…，zn→x(n-1)，zn+1→f（x，…，x(n-1)）+w（t）。有了估计值zn+1，控制量可表示为

根据上述ESO 的动态反馈线性化理论，由于系统的非线性变量集中式（5）中的第2 个方程，观测器的阶数比对象高一阶，故对式（5）中的第2 个方程构造相应的二阶ESO。

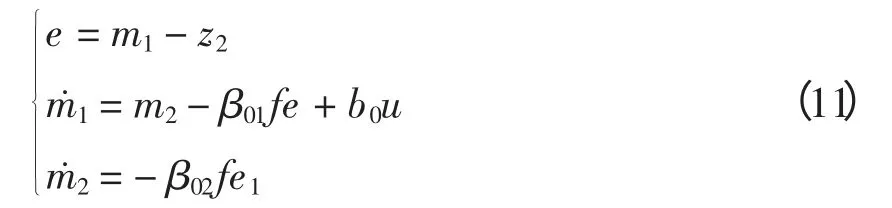
式中：m1为z2的估计值；m2为扩张变量，即

取控制量

2.3 变结构控制

变结构控制是一种控制系统的设计方法，可用于控制系统的跟踪、调节、自适应和不确定等，适用于线性和非线性系统。

根据变结构控制理论，取切换函数为

式中，c1为常数。

为了使滑模控制具有良好的动态品质，选择指数趋近律为

式中，ε、m 为正常数。

由式（5）、（16）、（17），可得

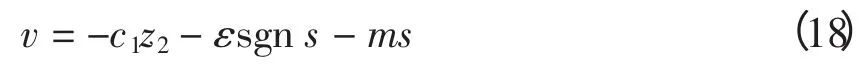
为了抑制滑模面上抖动，采用饱和函数代替式（18）的符号函数为

式（18）又可写成为

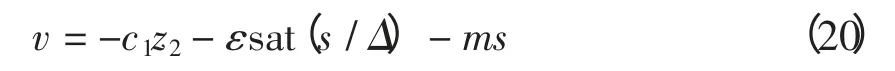
式（20）代入式（15），得非线性励磁控制规律为

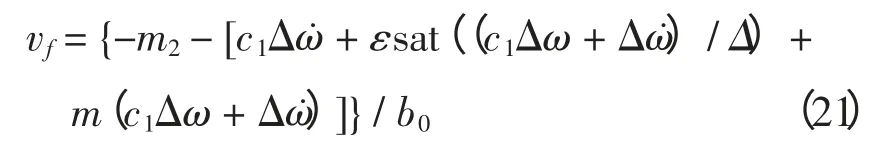
在式（21）的非线性励磁控制规律中加入机端电压偏差的比例积分控制，用以调节机端电压，得到最终的励磁控制规律为

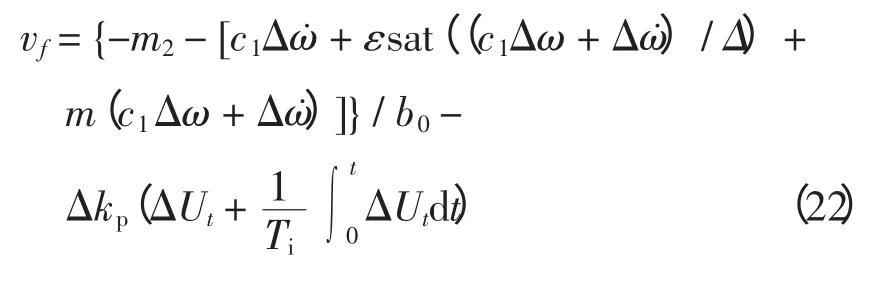
3 仿真分析

为论证本文所设计的非线性励磁控制器具有较好的控制效果，与文献[5]提出的非线性励磁控制器比较，图1 所示单机无穷大系统为例。

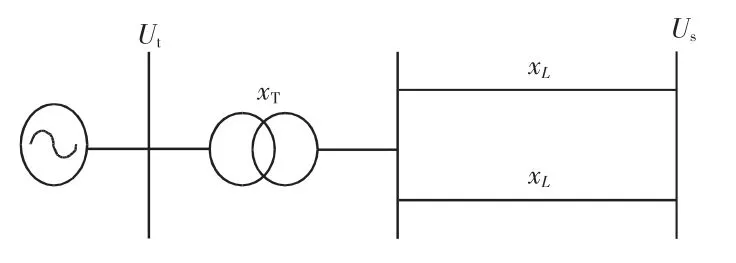
图1 单机无穷大系统Fig.1 Single-generator infinite bus power system

仿真软件采用Matlab。电力系统的模型参数为：xd= 1.0，xq= 0.6，xσ= 0.15，xd′ = 0.3，xd″ = 0.21，xq″=0.31，H=6 s，D=0.1，Td0=4 s，xT=0.088，xL=0.2。系统平衡点参数为：δ0= 22.15°，ω0= 1，Pe0=0.835，Qe0=0.26。设计的ESO 参数为：α1=0.5，α2=0.25，δ=0.01，β01=70，β02=10。设计变结构控制器参数为：c1=10，ε=0.1，m=10，Δ=0.1。PI 控制器参数为：kp=60，Ti=600。

3.1 机械功率扰动实验

机械功率Pm在t=1 s 时发生20%的阶跃扰动。机端电压Ut、功角δ、有功功率Pe和角速度偏差量Δω 的动态响应曲线如图2 所示。图中，实线为本文提出的改善机端电压的非线性励磁控制，虚线为文献[5]提出的非线性励磁控制器。

图2 表明，系统在小扰动情况下，常规非线性励磁控制器使发电机机端电压偏离扰动前的状态，而本文设计的励磁控制器使发电机机端电压在扰动后基本恢复到扰动前的值，同时使系统在扰动结束后较快地稳定下来。

3.2 三相短路实验

在t=1 s 时一回输电线路首端发生三相短路，0.2 s 后故障切除，系统单回路供电。发电机机端电压Ut、功角δ、有功功率Pe和角速度的偏差量Δω的动态响应曲线分别如图3 所示。

从图3 看出，本文设计的励磁控制器在大扰动下，发电机机端电压基本恢复到短路前的值，满足电压精度要求，同时系统功角和角速度进入稳态所需时间略短，对大干扰有一定的抑制作用。

3.3 参数扰动实验

令参数Td0发生+50%扰动，从而引起b0值变化，通过观察系统响应来验证控制器的鲁棒性。机端电压Ut、功角δ、有功功率Pe和角速度偏差量Δω 的动态响应曲线如图4 所示。由图4 可看出，当参数发生扰动时，由于ESO 补偿系统模型扰动，本文设计的励磁控制器恢复到稳态的时间比常规非线性励磁控制器要短，状态响应产生的偏差也小，说明本文方法具有较好的鲁棒性。

图2 机械功率扰动实验Fig.2 Mechanical power disturbance experiment

4 结语

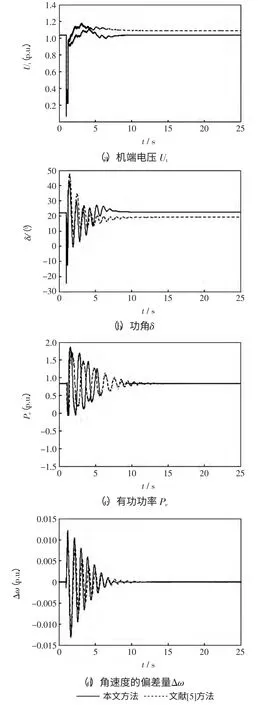
图3 三相短路实验Fig.3 Three-phase short circuit experiment

本文将微分几何理论、ESO 理论和变结构控制理论相结合，提出了一种基于微分几何和扩张状态观测器的非线性变结构励磁控制。仿真结果表明，在机械功率扰动和三相短路故障下，所设计的励磁控制器的控制效果优于常规非线性励磁控制器，能改善机端电压的调节精度，较好地保证发电机角速度、功角的稳定。同时，采用ESO 来估计未知参数和非线性模型，降低了控制器的复杂程度，对系统不确定性具有较好的鲁棒性。

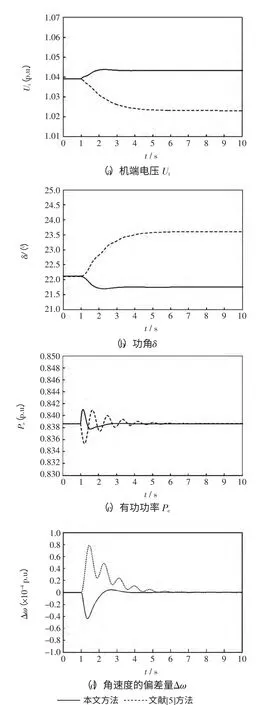
图4 参数扰动实验Fig.4 Parameter disturbance experiment

[1]万黎，邓长虹，陈允平（Wan Li，Deng Changhong，Chen Yunping）.考虑机端电压限制的多重非线性变结构励磁控制（Multi-layer nonlinear variable structure excitation control considering voltage limitation）[J]. 中国电机工程学报（Proceedings of the CSEE），2008，28（19）：86-92.

[2]王兴贵，黄忠良（Wang Xinggui，Huang Zhongliang）. 同步发电机励磁系统的智能变结构控制（Intelligent sliding mode variable structure control for synchronous generator excitation system）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（6）：79-82.

[3]韩京清（Han Jingqing）.从PID 技术到“自抗扰控制”技术（From PID technique to active disturbances rejection control technique）[J]. 控制工程（Control Engineering of China），2002，9（3）：13-18.

[4]韩京清.自抗扰控制技术[M].北京：科学出版社，1993.

[5]卢强，孙元章.电力系统非线性控制[M].北京：国防工业出版社，2008.

[6]孙元章，黎雄，戴和平，等（Sun Yuanzhang，Li Xiong，Dai Heping，et al）.同时改善稳定性和电压精度的非线性励磁控制器（A nonlinear excitation controller to improve both power system stability & voltage regulation accuracy）[J].中国电机工程学报（Proceedings of the CSEE），1996，l6（5）：332-336.

[7]李啸骢，程时杰，韦化，等（Li Xiaocong，Cheng Shijie，Wei Hua，et al）.一种高性能的非线性励磁控制（A high performance nonlinear excitation control for generator unit）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（12）：37-42.

[8]李啸骢，程时杰，韦化，等（Li Xiaocong，Cheng Shijie，Wei Hua，et al）.输出函数在单输入单输出非线性控制系统设计中的重要作用（Important effection of the output function in SISO nonlinear control system design）[J].中国电机工程学报（Proceedings of the CSEE），2004，24（10）：50-56.

[9]陈铁，舒乃秋（Chen Tie，Shu Naiqiu）.非线性励磁控制方法的研究（Research of the nonlinear excitation based on the direct feedback linearization）[J]. 继电器（Relay），2005，33（19）：28-30，35.

[10]王奔，毛宗源（Wang Ben，Mao Zongyuan）. 大型同步发电机变结构励磁控制（Giant synchronous generationset′s Variable structure controller）[J].电力系统及其自动化学报（Proceedings o f the CSU-EPSA），1998，10（2）：1-6，14.

[11]胡跃明.非线性控制系统理论与应用[M].北京：国防工业出版社，2002.