应对大范围潮流转移的在线电压稳定判别指标
唐晓骏,程振龙,张 鑫,李再华,李 晶,罗红梅
(1.中国电力科学研究院,北京100192;2.华北电力大学电气与电子工程学院,保定071003)
国外大电网相继发生的电压崩溃事故[1-4],给电力工业带来深刻警示,有力地推进了电压稳定领域的深入发展,但到目前为止,电压稳定问题的理论体系尚未完善。20 世纪90 年代以前电压稳定的研究主要集中于静态稳定方面,目前动态电压稳定分析方法的研究正在不断深入。日本强调事故后电压控制能力的增强,法国则侧重于事故发生前紧急状态下的预防措施。意大利电网、瑞典电网、加拿大魁北克水电局等单位也投运了防止电压崩溃的控制系统。国内研究机构在电压稳定方面做了大量的工作,积累了丰富的经验[5-6]。随着直流输电技术的广泛应用,交直流混联输电给电网电压稳定问题带来了新的特点[7]。
从故障对电网暂稳特性影响的角度来看,可以简单将故障分为两类:一类为对系统无短路冲击,仅考虑大规模潮流转移引起的稳定问题,如直流闭锁故障、发电机无故障跳闸故障;另一类为对系统有短路冲击,同时需要考虑短路冲击和大规模潮流转移引起的稳定问题,如直流逆变站附近交流系统短路故障等。仅从潮流转移的角度来看,第1 类故障后的潮流转移与静态电压稳定考虑的负荷缓慢增长引起的潮流转移具有一定相似性,但两者的持续时间相差很大,前者考虑数十毫秒期间系统的暂态电压稳定水平,后者则考虑数分钟乃至更长时间系统的静态电压稳定水平,目前分别采用暂态、静态电压稳定研究方法进行评估。考虑到对于第1 类故障,由于不考虑短路冲击,故障前后系统条件变化不大,加之采用合适的静态电压稳定计算方法时可以考虑部分类型负荷响应和发电机响应特性,因此考虑在一定条件下可以采用静态电压稳定方法近似评估第1 类故障下电网的暂态电压稳定水平。
本文针对第1 类故障,首先采用PSD-ST 潮流和暂态稳定分析计算探讨验证了在一定条件下可以近似采用静态电压稳定分析的方法来研究第1类故障可能引发的暂态电压失稳问题;在总结现有静态电压稳定指标优缺点的同时,基于PMU 量测信息提出了综合考虑有功、无功潮流影响的电压稳定在线评估指标;采用基于实际电网的等值系统,仿真验证了所提指标对静态/暂态电压稳定极限评估的有效性。
1 应对潮流转移的静态、暂态电压稳定分析结果对比
搭建简化交直流混联系统模型如图1 所示。送端为等值无穷大发电机组,通过变压器升压至500 kV 交直流混联系统外送;500 kV 交流通道阻抗参数为0.000 13+j0.002 91(基准功率100 MVA),直流通道输送能力为双极3000 MW,整流站、逆变站分别配置1200、1640 Mvar 滤波电容器;受端电网通过500/220 kV 变压器降压,负荷等值在220 kV 母线,负荷功率因数为0.95。

图1 简化交直流混联系统结构Fig.1 Simplified AC/DC hybrid system structure
1.1 计算交直流混联系统的暂态电压稳定极限
假定负荷为恒功率负荷,0 s 发生直流单级闭锁故障,0.1 s 故障清除并切除直流整流侧、逆变侧滤波电容600、820 Mvar,送端不采取切机措施,全部功率转移至交流通道外送,计算交流通道的暂态电压稳定极限送电能力。本文采用工程实用暂态电压稳定判据,在电力系统受到扰动后的暂态过程中,负荷母线(220 kV 或110 kV 母线)电压能够在10 s 以内恢复到0.80 标称电压以上。计算结果如表1 所示。

表1 暂态电压稳定极限结果表Tab.1 Transient voltage stability limitation MW
1.2 计算交直流混联系统的静态电压稳定极限
采用PSD-ST 潮流程序,在受端电网按照一定负荷增长模式增长负荷,直至潮流不收敛。按照纯有功负荷增长模式计算得到的静态电压稳定极限为5 164 MW,按照恒功率因数0.95 增长模式计算得到的静稳极限为4 748 MW。
对比静态、暂态电压稳定极限结果可以看出:
(1)采用不同的负荷模型时,暂态电压稳定计算结果有所不同。依据工程经验,若以直流闭锁故障后系统崩溃为暂态失稳目标,则不同负荷模型下计算结果相差较大。若以直流闭锁故障后负荷侧母线电压持续低于0.8 p.u. 为暂态电压失稳目标,则不同负荷模型下计算结果相差较小,平均误差可控制在3%以内,相对而言,采用100%恒功率模型更为保守,得到的暂态电压稳定极限相对较小。
(2)采用不同的负荷增长模式时,静态电压稳定计算结果有所不同。若采用恒功率因数负荷增长模式,相对恒有功负荷增长模式而言,受端电网无功负荷有所增加,系统更易接近静态电压失稳。从直观上看,当直流发生单级闭锁故障时,仅有功功率大范围转移至交流通道,因此采用静态电压稳定方法分析时应采用纯有功负荷增长模式较为合理。但是在实际系统中,一般正常运行时,需要控制直流逆变侧与交流系统交换功率因数在0.95左右即可,无法实时控制交直流系统逆变侧无功交换为零。因此,采用静态电压稳定方法分析时,采用恒功率因数负荷增长模式,考虑一定容量的无功负荷转移可能更为接近实际情况。从仿真计算的结果来看,采用恒功率因数负荷增长模式得到的静态电压稳定极限4 748 MW,更接近系统暂态电压稳定极限4 893 MW。
通过对上述简单系统的静态、暂态电压稳定极限计算及对比可以看出,对于直流闭锁故障,采用合理的静态电压稳定极限方法可以近似逼近暂态电压稳定极限,为暂态电压稳定评估和计算提供了一条新的途径。
2 电压稳定评估指标
2.1 电压稳定评估指标研究现状
随着电网互联规模的不断增大,电压失稳也逐步表现出新的特征,既可能发生在局部地区低电压等级电网个别母线,也可能发生在骨干高电压电网形成电压崩溃,特性复杂,具有一定的隐蔽性和突发性。目前常用的静态电压稳定指标包括灵敏度指标[9]、负荷裕度指标[10]、雅可比矩阵最小奇异值指标[11]、局部电压稳定L 指标[12]等,取得了较好的静态电压稳定评估效果,但这些方法都需要进行不同程度的复杂计算,难以应用于需要快速计算的在线电压稳定监测系统。
随着大电网广域测量/监视系统WAMS(wide area measurement system)的不断建设和完善,基于WAMS 强大的在线同步测量能力和高速通信网络,使得实现全局性的电压稳定在线监测成为可能[13]。目前基于WAMS 的电压稳定指标可分为如下两类:
(1)基于戴维南等值的快速评估指标。文献[14]基于节点的戴维南等值电路,通过多项式拟合研究节点电压-电流V-I 关系,从而根据V-I 平面上V 轴和I 轴所围的最大面积得到系统的运行极限;文献[15-17]进一步将戴维南等值方法引入故障后暂态电压稳定评估,提出了基于时域仿真、基于全微分的戴维南等值跟踪算法,同时指出当负荷不满足恒定功率因数变化特性时,将负荷节点等效阻抗与该节点的网络戴维南等值阻抗相等作为电压稳定的临界条件是无效的,大大推进了基于戴维南等值方法的应用。但是,为准确获取戴维南等值参数需要进行大量计算,难以满足在线快速计算的需求。
(2)基于线路/路径的快速评估指标。文献[18]提出静态电压稳定指标LVSI,其参数可由WAMS实时测量,其推导是基于时间断面,反映的是系统各支路和整体在同一时间断面上的电压稳定水平以及相对稳定裕度,对于WAMS 技术在电压监测领域的应用具有一定的指导意义,但在指标定义上还存在一定的偏差性。
相对于在线获取等值系统戴维南等值阻抗而言,获取线路实时功率、母线实时电压等信息更为容易,且对于生产运行人员来说,更为直观和易于理解。在文献[18]的基础上,本文在考虑有功传输对系统静态电压稳定极限影响的基础上,进一步考虑无功传输对其影响,提出了综合考虑有功、无功传输影响的电压稳定在线评估指标,该指标既可有效评估负荷缓慢增长方式下的静态稳定水平,也可有效评估直流闭锁故障下系统的暂态稳定水平,系统仿真算例验证了该指标的有效性。该指标计算量小,精度高,可应用于在线电压稳定分析与监测系统。
2.2 在线电压稳定评估指标推导
静态电压稳定分析中,通常采用无穷大系统带负荷的简单两节点系统模型,支路多采用阻抗模型或纯电抗模型,忽略线路对地电纳的影响,如图2 所示。结合目前实际电网仿真数据,为简化系统规模,负荷多等值在220 kV 母线或220 kV 变压器的110 kV 母线,线路充电功率相对较小,因此本文研究中不考虑线路充电功率的影响。

图2 线路模型Fig.2 Model of transmission line
静态电压稳定极限,目前多以输电线路达到最大输电能力为极限,多以有功功率输送裕度为静态电压稳定裕度。但在大功率潮流转移中,除有功功率外还可能有较大的无功穿越,导致线路输电极限大幅快速下降,所以应考虑有功、无功传输相结合的裕度指标。
首先计算图2 所示线路送受端两侧母线电压差为

展开得到
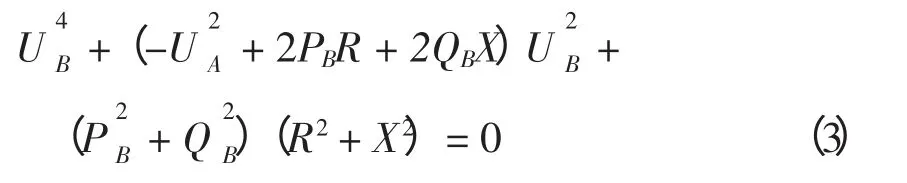
解得

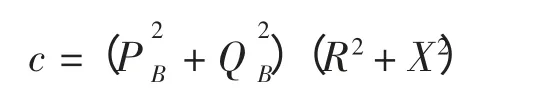
当满足:Δ=b2-4ac=0 时,电压存在唯一解为
即,在任一时间断面,都可以基于线路输送功率和送端母线电压建立一条PV 曲线,曲线的初始点为电网当前运行点,曲线的拐点为电压崩溃点。为达到电压崩溃点前,对应任一运行点,电压存在不唯一解;在电压崩溃点,电压存在唯一解,对应公式(4)中的b2-4ac=0。
因此,建立新指标为
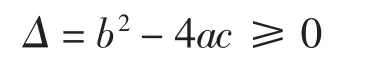

实际应用时,该指标仅需从PMU 中获取线路受端的有功功率、无功功率,线路送端母线电压和线路电阻、电抗参数,即可求得线路目前运行状态,判断其距离极限的裕度。LPQ指标越接近1,则系统越处于紧张状态,接近静态电压失稳边界。与其他指标相比,该指标所需信息量少、结构简单、物理意义明确,易于实现。
在判断电网的静态电压稳定水平时,需要对全部负荷供电线路进行LPQ指标计算,考虑到电压稳定首先发生在较为薄弱的线路上,此类线路的LPQ指标相对其他线路较大,因此取全部线路LPQ指标中的最大值作为系统的电压稳定指标,定义为

式中:S 代表所研究电网的支路集合;LPQk代表支路k 的电压稳定指标。
若对电网内全部线路进行LPQ指标计算,计算量大且无必要。在实际系统应用时,可预先通过灵敏度分析、特征值分析、图论分析等方法,并结合工程经验,大致确定需要分析的电网薄弱环节,可大幅减少计算量,进一步提高电压稳定评估效率。
3 仿真分析
以实际的交直流系统为原型,构建算例系统如图3 所示,该算例中包含交直流送电通道和明确的送受关系。在BUS1 和BUS3 形成典型的交直流混联系统,负荷主要分布在BUS6 和BUS8 处,负荷功率因数0.95。

图3 交直流混联系统Fig.3 AC/DC hybrid power system
首先,按照恒功率因数负荷增长模式,计算BUS2 和BUS3 之间交流通道的静态电压稳定极限,如表2 所示。随着远端负荷的不断增加,交流通道有功、无功潮流逐步增加,受端BUS3 母线电压逐步降低,LPQ指标不断增大,计算得到的静态电压稳定极限为3 450 MW,此时对应的LPQ指标为0.978 2,非常接近1,说明系统达到静态电压稳定极限,证明了该指标的有效性。
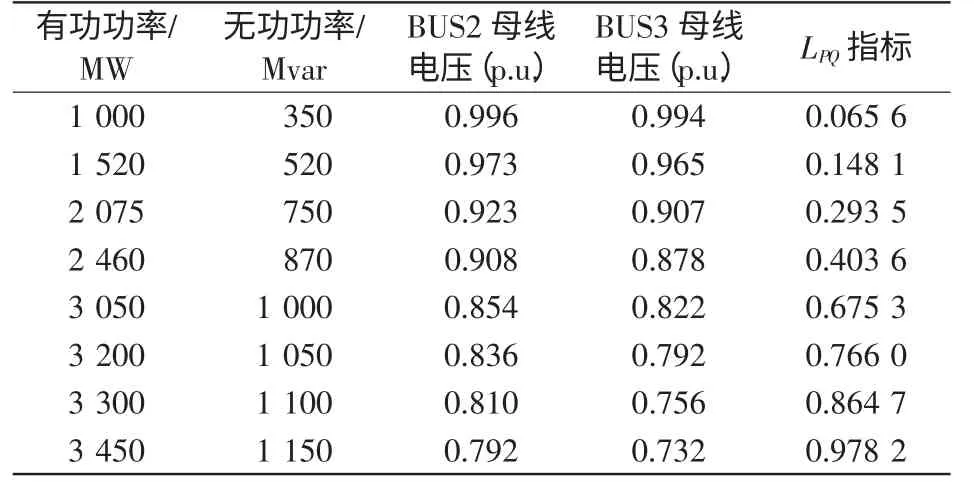
表2 交流通道的静态电压稳定极限Tab.2 Static voltage stability limit of AC transmission line
以直流双极闭锁故障校核交流通道的暂态电压稳定极限。假设0 s 发生直流双极闭锁故障,0.1 s切除两侧配套滤波电容,约3 000 MW 电力转由交流通道外送,交流线路受端BUSs3 母线电压显著降低,如图4 所示。依据第1 节中的工程实用暂态电压稳定判据,可以看出3.88 s 左右BUS2 和BUS3之间交流通道达到暂态电压稳定极限3 640 MW。

图4 BUS2 和BUS3 母线电压Fig.4 Bus voltage of BUS2 and BUS3

图5 BUS2 和BUS3 之间交流通道的功率变化曲线Fig.5 Active power curve of AC transmission line between BUS2 and BUS3
暂态过程中,BUS2 和BUS3 之间交流通道的功率变化曲线如图5 所示,依据图4 和图5 可以做出故障后任一时刻BUS2 和BUS3 之间交流通道的LPQ指标,如图6 所示。可以看出,发生直流闭锁故障后,交流通道上潮流大幅变化,母线电压显著降低,LPQ指标逐步接近1,在3.88 s 左右最接近1,达到暂态电压稳定极限。因此,故障后依据PMU就地测量信息,实时计算各条线路的LPQ指标,可有效评估电网的实时暂态电压稳定水平,为后继
采用预防电压失稳的紧急控制措施提供参考。

图6 电压稳定指标曲线Fig.6 Curve of bus voltage stability index
4 结论
(1)依据故障性质的不同,交直流混联系统中暂态电压失稳问题可大致分为两类,一类为对系统无短路冲击,仅考虑大规模潮流转移引起的稳定问题,如直流闭锁故障、发电机无故障跳闸故障;另一类为对系统有短路冲击,同时需要考虑短路冲击和大规模潮流转移引起的稳定问题,如直流逆变站附近交流系统短路故障等。
(2)对于第一类问题,采用工程实用判据的暂态电压稳定极限水平与一定条件下的静态电压稳定极限水平差异较小。即不考虑短路冲击时,可以采用合理的静态电压稳定极限方法近似逼近暂态电压稳定极限。
(3)综合考虑有功、无功传输影响的电压稳定在线评估指标LPQ,仅需少量就地信息即可快速评估系统的静态、暂态电压稳定水平。实际电网仿真分析表明,该指标评估结果有效,结构简单,物理意义明确,易于在线实现。
[1]卢卫星,舒印彪,史连军(Lu Weixing,Shu Yinbiao,Shi Lianjun).美国西部电力系统1996 年8 月10 日大停电事故(WSCC disturbance on August 10,1996 in the United States)[J].电网技术(Power System Technology),1996,20(9):40-42.
[2]薛禹胜(XueYusheng).综合防御由偶然故障演化为电力灾难——北美“8·14”大停电的警示(The way from a simple contingency to system-wide disaster—Lessons from the Eastern Interconnection Blackout in 2003)[J].电力系统自动化(Automation of Electric Power Systems),2003,27(18):1-5,37.
[3]林伟芳,孙华东,汤涌,等(Lin Weifang,Sun Huadong,Tang Yong,et al).巴西“11·10”大停电事故分析及启示(Analysis and lessons of blackout in Brazil power grid on November 10,2009)[J].电力系统自动化(Automation of Electric Power Systems),2010,34(7):1-5.
[4]汤涌,卜广全,易俊(Tang Yong,Bu Guangquan,Yi Jun).印度“7.30”、“7.31”大停电事故分析及启示(Analysis and lessons of the blackout in Indian power grid on July 30 and 31,2012)[J].中国电机工程学报(Proceedings of the CSEE),2012,32(25):167-174.
[5]刘益青,陈超英,梁磊,等(Liu Yiqing,Chen Chaoying,Liang Lei,et al).电力系统电压稳定性的动态分析方法综述(Review of dynamical analysis art of voltage stability in power systems)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2003,15(1):105-108.
[6]邹德旭,贺仁睦,司大军(Zou Dexu,He Renmu,Si Dajun).负荷模型对电力系统动态稳定的影响(Effects of load model on dynamic stability in power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(1):118-122.
[7]汪娟娟,张尧,夏成军,等(Wang Juanjuan,Zhang Yao,Xia Chengjun,et al).交直流电力系统暂态电压稳定性综述(Survey of studies on transient voltage stability of AC/DC power system)[J].电网技术(Power System Technology),2008,32(12):30-34.
[8]Q/GDW 404—2010,国家电网安全稳定计算技术规范[S].
[9]Flatabo N,Fosso O B,Ognedal R,et al. A method for calculation of margins to voltage instability applied on the Norwegian system for maintaining required security level[J].IEEE Trans on Power Systems,1993,8(3):920-928.
[10]杨晓萍,张强,薛斌,等(Yang Xiaoping,Zhang Qiang,Xue Bin,et al).考虑静态电压稳定性的多目标无功优化(Multi-objective reactive power optimization with static voltage stability)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(1):138-144.
[11]冯治鸿,刘取,周双喜,等(Feng Zhihong,Liu Qu,Zhou Shuangxi,et al).多机电力系统电压静态稳定性的特征结构分析法(An eigen-structure analysis method of the steady-state voltage stability in multimachine systems)[J].清华大学学报(Journal of Tsinghua University),1991,31(4):19-27.
[12]Berizzi A,Finazzi P,Dosi D,et al. First and second order methods for voltage collapse assessment and security enhancement[J]. IEEE Trans on Power Systems,1998,13(2):543-551.
[13]张鹏飞,罗承廉,孟远景,等(ZhangPengfei,Luo Chenglian,Meng Yuanjing,et al).基于WAMS 的河南电网动态特性监测分析(Wide area monitoring and analysis of Henan power system dynamic performance)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(4):65-69.
[14]刘楠(Liu Nan).在线电压安全评估算法、指标及系统构建研究(Study on Algorithms Related to Voltage Security on-Line Assessment,Index and System Building)[D]. 北京:中国电力科学研究院(Beijing:China Electric Power Research Institute),2010.
[15]汤涌,孙华东,易俊,等(Tang Yong,Sun Huadong,Yi Jun,et al). 基于全微分的戴维南等值参数跟踪算法(Tracing algorithm for Tthevenin equivalent parameters based on complete differential equation)[J]. 中国电机工程学报(Proceedings of the CSEE),2009,29(13):48-53.
[16]汤涌,易俊,侯俊贤,等(Tang Yong,Yi Jun,Hou Junxian,et al).基于时域仿真的戴维南等值参数跟踪计算方法(Calculation method for Thevenin equivalent parameters based on time domain simulation)[J].中国电机工程学报(Proceedings of the CSEE),2010,30(34):63-68.
[17]汤涌,林伟芳,孙华东,等(Tang Yong,Lin Weifang,Sun Huadong,et al).考虑负荷变化特性的电压稳定判据分析(Analysis of voltage stability criterion considering load characteristics)[J]. 中国电机工程学报(Proceedings of the CSEE),2010,30(16):12-18.
[18]刘道伟,谢小荣,穆钢,等(Liu Daowei,Xie Xiaorong,Mu Gang,et al).基于同步相量测量的电力系统在线电压稳定指标(An on-line voltage stability index for power system based on synchronized phasor measurement)[J].中国电机工程学报(Proceedings of the CSEE),2005,25(1):13-17.

