含风电场的混合机会约束经济调度模型

盛四清，孙晓霞

（华北电力大学电气与电子工程学院，保定071000）

随着传统化石能源的日益枯竭以及环境保护问题的日益严峻，以风电为代表的清洁可再生能源得到了极大的重视和发展。然而风电固有的间歇性和波动性给电力系统的调度运行带来了严峻的挑战，因此含风电场的电力系统经济调度问题也成为了研究热点[1-3]。

风电对调度的影响主要体现在其出力的不确定性上。现有文献对风电的处理可分为3 类[4]：确定性模型、随机模型以及模糊模型。确定性模型就是调度时考虑风电的全部备用，这种方法会大大提高系统的运行成本，显然不可取。可行的处理是将风电出力视为不确定变量，通过引入机会约束来协调风险和成本之间的关系。如文献[5-6]将风电出力视为随机变量，通过风速-功率曲线转换得到相应的概率分布参数。然而由于风电出力受到温度、湿度、气压等气象因素的影响，预测方法并不具有统计性质的误差，因此采用模糊参数表示更为合理。文献[7]采用梯形模糊数来表示风电出力的不确定性，指出梯形隶属度函数与人们研究不确定性问题的思考方式更为相近。但是此文将风电出力笼统的用给定分布表示，并没有考虑到风电出力的时序性。在自然条件下，风电早晚出力有较大波动，因此对风电功率的预测误差进行建模更为合理。文献[8-10]将风电的预测值视为确定量，将风电出力的模糊性体现为预测误差的模糊性，认为风电预测误差的隶属度服从柯西分布[11-13]，并指出采用误差建模可以减少不确定可行域的维度，具有较好的启发性。本文沿用了这种误差建模的思路。

众所周知，电力系统中除了风电功率的不确定性，负荷出力也存在不确定性。个别文献也对此进行了研究，文献[14]将风电和负荷都用模糊参数来表示，建立了基于可信性理论的模糊机会约束机组组合模型。这种将系统中存在的多重不确定因素统一为单一的随机规划或者模糊规划的做法显然是一种简化处理。现实情况中，随机变量与模糊变量往往不是分离或对立的关系，更可能同时存在于一个系统中。风电由于受到气象、环境等因素的影响，出力往往具有模糊性；而负荷每日的变化则具有较高重复性，由历史统计数据完全可以得到其概率模型的变化规律。考虑同时含有模糊变量和随机变量的多重不确定因素的经济调度模型将更加符合实际，但是也造成了求解难度的增加。

不确定规划理论为解决此类问题提供了理论依据。一个复杂的决策系统通常具有多维性、多样性、多功能性和多准则性，并且含有多重不确定因素[15]。随机规划和模糊规划在解决具有单重不确定因素的问题时，收到了很好的效果，但是对于具有多重不确定性的优化问题则显得无能为力[16]。不确定规划理论是在传统随机规划和模糊规划基础上的扩展。机会约束模型是不确定规划理论中的一大分支，主要用于解决约束条件中含有不确定变量，且必须在观测到不确定变量的实现之前做出决策的问题。由于风电和负荷出力不确定性因素的影响，使得调度决策结果可能无法满足系统全部的约束条件，为此采取一种妥协的办法，即牺牲一部分强制约束，允许一定风险的存在。机会约束规划理论的提出成为解决含不确定因素调度问题的有力工具。调度人员能够清晰地看到调度决策的风险与成本之间的关系，这样建立的模型将更加贴合实际而且易于操作。

本文将不确定规划理论的最新内容引入到含风电场电力系统动态经济调度问题的研究中。综合考虑了调度运行中存在的多重不确定因素的不同特性，将风电预测误差和负荷预测误差分别表示成模糊变量和随机变量，建立了同时含有模糊变量和随机变量的混合机会约束经济调度模型。针对所建模型，采用模糊模拟和随机模拟技术相结合的混合模拟求解策略进行求解。算例分析说明了该模型对于解决含风电场电力系统动态经济调度问题的可行性。

1 混合机会约束规划模型

含有多重不确定因素问题的数学规划模型可以写成

式中：x 为决策变量；ε 为随机变量；η 为模糊变量；f 是目标函数；gj（x，ε，η）为约束条件函数；m 为约束条件的个数。

因为约束条件中出现了不确定变量，不再是一个确定性模型，所以不能给出一个确定的可行集。根据Charnes 和Cooper 等在处理随机规划和模糊规划时采取的方法，引入机会约束的思想，将约束条件处理成在给定置信水平下成立。由于模型中含有多重不确定变量，因此可以分开考虑，将模糊和随机因素看成是模糊机会和随机机会的并存，则有同时含有模糊变量和随机变量的混合机会约束规划模型[15]为

式中：α 和β 分别为事先给定的对约束条件中对应随机变量和模糊变量的置信水平；Pos{}表示{}中事件成立的可能性，Pr{}表示{}中事件成立的概率。

2 含风电场电力系统动态经济调度的混合机会约束模型

2.1 不确定因素的处理

将风电和负荷出力的不确定性表示为预测误差的不确定性，即认为预测值为确定量，对预测误差进行不确定建模。针对风电和负荷的不同特性，所建模型如下。

风电出力表示为

式中：PWt为风电t 时刻的出力；PWt′为风电t 时刻出力的预测值，为一个确定量；eWt为风电t 时刻的预测误差。

由于受到气象、环境等因素的影响，风电出力本身不具有统计性质的概率分布函数，因此采用模糊变量描述更符合其特性。如此，可将风电出力的预测误差eWt视为一个三角模糊变量，其三角模糊参数及隶属度函数可表示为

式中，εWt的数值可由风电预测值的百分比决定，具体比例系数可由风电出力的历史数据确定。

负荷出力表示为

式中：PLt为负荷t 时刻的出力；PLt′为负荷t 时刻的预测值，为一确定量；eLt为t 时刻的负荷预测误差。

由于每日负荷具有较高的重复性，负荷预测误差对预测时间范围不是特别灵敏，通常与任意给定小时的负荷大小成比例，因此一段时间内的负荷预测误差可以表示为高斯统计变量，则有

式中，k 一般为1。

2.2 目标函数

实际系统中，汽轮机进气阀突然开启时会在机组耗量特性曲线上叠加一个脉动效果，即产生阀点效应，忽略它会使求解结果受到明显影响。本文计及阀点效应引起的耗量增加，模型为

式中：F 为火电机组的总运行成本；Fit为第i 台火电机组t 时刻的煤耗量；ai、bi、ci为第i 台火电机组的燃料费用系数；ei、fi为第i 台火电机组的阀点效应参数；Pit为第i 台火电机组t 时刻的调度出力；Pimin为第i 台火电机组出力的最小值；T 为一个调度周期；N 为火电机组的台数。

2.3 约束条件

2.3.1 系统约束

传统调度中，系统的功率平衡约束表示为

显然这样的调度决策没有考虑风电和负荷出力的不确定因素。这里将预测值视为确定量，通过预测误差体现风电和负荷出力的不确定性，引入机会约束则有如下的约束条件：

式中：α 对应约束条件中随机变量eLt的置信水平；β 对应约束条件中模糊变量eWt的置信水平。

2.3.2 火电机组约束

火电机组的出力约束为

式中，Pimax为第i 台火电机组出力的最大值。

火电机组的爬坡速率约束为

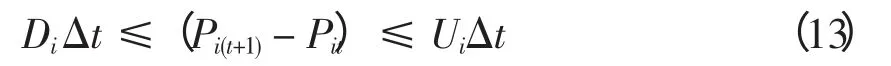
式中：Di、Ui分别为第i 台火电机组有功出力的下降速率和上升速率；Δt 为一个时间段的时长。

3 模糊随机混合机会约束模型的求解

对于模型中的模糊随机约束条件，任意给定一个决策变量x，当且仅当存在一个清晰向量η0，使得当μ（η0）≥β 成立时有Pr{g（x，ε，η0）≤0}≥α 成立，则x 为一个可行解[15]。具体步骤如下。

（1）先在η 的β 水平截集中均匀的生成一个清晰向量η0。

如果模糊向量η 的β 水平截集过于复杂而难以确定，则可以从包含β 水平截集的一个超几何体Ω 中抽取向量η0，接受与否依赖于μ（η0）≥β 是否成立。

（2）将满足条件的η0代入，运用随机模拟技术检验Pr{g（x，ε，η0）≤0}≥α 是否成立。

从ε 的概率分布Φ（ε）中产生N 个独立的随机变量ε1，ε2，…，εN，令N′为N 次实验中g（x，ε，η0）≤0 成立的次数，如果N′/N ≥α，则有Pos{Pr{g（x，ε，η0）≤0}≥α}≥β 成立，否则重新产生清晰向量η0，检验满足模糊约束后，然后进行随机模拟检验。

（3）经过给定的次数K 后，如果还是没有生成清晰向量η0，使得该式成立，则决策变量x 为不可行解。

根据上述步骤可编制基于模糊随机混合模拟的进化算法程序，算法流程如图1 所示。

图1 算法流程Fig.1 Flow chart of algorithm

4 实例计算与分析

4.1 基本数据与参数

为了验证本文所提模型的可行性，以某系统风电、火电联合调度为例，取调度周期为6 个时段。该系统6 时段的负荷预测值以及风电预测值见文献[17]。该系统配有10 台火电机组，总装机容量为2 358 MW，各参数见文献[18]。

利用Matlab 编写基于模糊随机混合模拟的进化算法程序，初始产生100 个染色体，择优选取20个进行进化计算，迭代次数取500。

4.2 计算结果与分析

为了减少模拟计算的误差，最后的求解结果为重复40 次后取平均值。当置信水平取α=β=0.8时，优化解见表1，优化函数值为F=187 105 ＄。

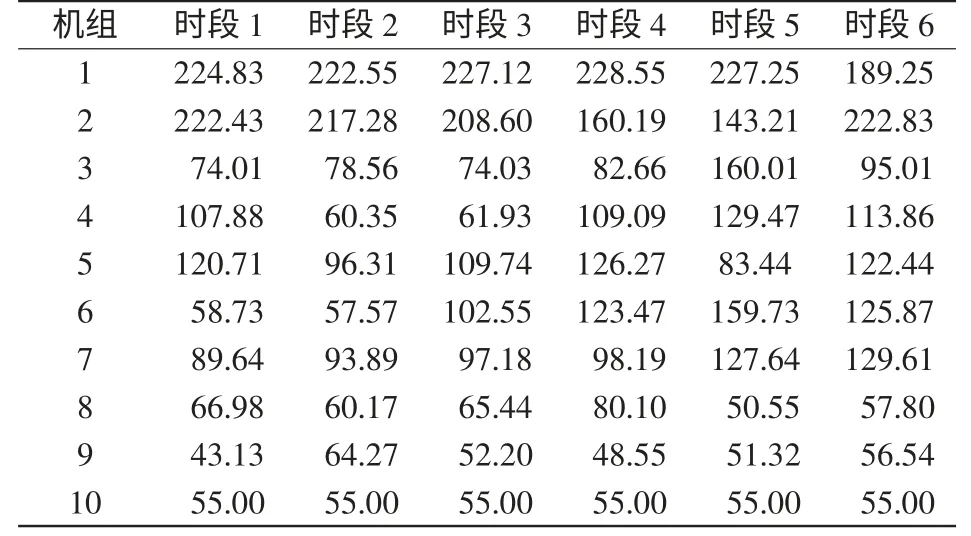
表1 优化调度结果Tab.1 Optimal dispatch results MW

表1 中的数据在时段3、4 出现了局部波动，这可能是由于随机模拟和模糊模拟使得误差在同一时刻强叠加导致的。由图2 可知，当进化到第319 代时，算法已经收敛。

图2 算法收敛曲线Fig.2 Convergent curve of algorithm

表2 不同方案优化结果Tab.2 Optimal results with different scheduling schemes

表2 为当α=β=0.8 时，是否考虑阀点效应的运行成本对比。由表中数据可以看出，当不考虑火电机组的阀点效应时，显然成本较低；而当计及阀点效应时运行成本有明显的增大。这是符合实际的结果，模型中是否考虑了阀点效应对调度决策有一定的影响，考虑阀点效应将更加符合实际情况，也使得调度结果更加真实。

表3 和表4 为选择不同置信水平下目标函数值的优化结果对比。

表3 不同随机置信水平下的运行成本Tab.3 Cost with different random confidence levels

表4 不同模糊置信水平下的运行成本Tab.4 Cost with different fuzzy confidence levels

（1）保持β=0.8 不变，改变α 的值。

随机置信水平α 的大小反映了不确定环境下随机变量对应的约束条件的实现机会。由表3 数据可知，α 对应风险的度量，当α 较大时，火电和风电的联合出力大于负荷的概率大，对应较高的可靠性和较小的失负荷风险水平，此时火电的运行成本高；当α 较小时，联合出力大于负荷的概率小，对应较大的失负荷风险和低可靠性，此时火电的运行成本低。随着置信水平的不断提高，失负荷的风险逐渐减小，而目标优化结果则逐渐趋于劣势，系统总的运行成本不断增加，时段6 的成本差达到4 456 ＄，可见不同风险对于调度结果的影响。调度人员可以根据计算结果判断不同调度决策可能取得的成本以及风险之间的关系，根据系统的实时情况设定恰当的置信水平并选取合适的优化调度方案。

（2）保持α=0.8 不变，改变β 的值。

模糊置信水平β 的大小反映了不确定环境下模糊变量实现的可能性，这里体现为调度人员对风电预测值准确度的不同估计。由表4 数据可知，在风险相同的情况下，β 越大说明调度人员对预测结果越乐观，认为风电的预测精度高，此时的预测误差较小，引起的火电功率调整费用也少，系统总的运行成本低；β 较小时说明调度人员对风电预测结果持悲观态度，认为风电预测精度较低，预测误差较大，因此需要更多的功率调整容量，使得火电的总运行成本升高。

算例对比中运行成本随置信水平的提高并没有如表3 那样大幅度变化，这是因为风电在整个系统中所占的比例较小，风电预测误差的波动可能会淹没在负荷预测误差的大幅度波动中。在实际运行中，针对不同的风电场，可以根据历史数据进行总结，设定不同的风电预测值准确度指标，对风电出力进行合理评估。

综上，在合理考虑不确定因素的基础上，所建模型能事先对系统的成本和风险进行管理。

5 结语

本文综合考虑了含风电场电力系统动态经济调度运行过程中存在的多重不确定因素，将风电和负荷出力的不确定性表示为预测误差的不确定性。针对风电和负荷出力的不同特性，对风电预测误差和负荷预测误差采用区别建模，提出同时含有模糊变量和随机变量的混合机会约束经济调度模型，并给出了处理该模型的混合模拟求解策略。模型通过引入模糊机会和随机机会来控制约束条件中两类不确定变量的变化：随机置信水平反映了系统失负荷的风险，运行成本随风险的增大而减少；模糊置信水平则体现了调度人员对风电预测值准确度的不同估计。调度人员可根据系统实际情况兼顾成本和风险，实现最优化决策。

与现有调度方法相比，本文所提方法能量化调度方案的实现概率和运行成本之间的关系，作为初步探究，本文的重点在于构造了考虑多重不确定因素的含风电场电力系统动态经济调度模型。在现有预测水平下，考虑随机与模糊的并存能较为准确地描述风电和负荷的不同特性。本文没有就预测误差的具体建模过程进行深入研究，而是直接引用前人成果。由于问题本身的复杂性，算法的求解效率并不高。如何提高计算速度，兼顾火电的环境成本因素是下一步需研究的内容。

[1]唐民，董小娇，文强（Tang Min，Dong Xiaojiao，Wen Qiang）.计及网络参数不确定的含风电场安全经济调度（Security economic dispatch of power system integrated with wind farms considering uncertainty of network parameters）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2012，24（2）：27-34.

[2]孙倩，李林川，崔伟，等（Sun Qian，Li Linchuan，Cui Wei，et al）.考虑风电不确定性的电力系统日运行方式优化（Optimization of daily operation of the power system considering the uncertainty of wind power）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（4）：122-127.

[3]刘岱，庞松岭（Liu Dai，Pang Songling）.风电集中接入对电网的影响分析（System impacts analysis for interconnection of wind farm and power grid）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（3）：156-160.

[4]周玮，孙辉，顾宏，等（Zhou Wei，Sun Hui，Gu Hong，et al）.含风电场的电力系统经济调度研究综述（A review on economic dispatch of power system including wind farms）[J].电力系统保护与控制（Power System Protection and Control），2011，39（24）：148-154.

[5]于佳，任建文，周明（Yu Jia，Ren Jianwen，Zhou Ming）.基于机会约束规划的风-蓄联合动态经济调度（A chance-constrained programming based dynamic economic dispatch of wind farm and pumped-storage power station）[J].电网技术（Power System Technology），2013，37（8）：2116-2122.

[6]Yuan Y，Li Q，Wang W. Optimal operation strategy of energy storage unit in wind power integration based on stochastic programming[J].IET Renewable Power Generation，2011，5（2）：194-201.

[7]孙翠英（Sun Cuiying）.基于可信性理论含规模化风电的机组组合问题研究（Credibility Theory Based Research on Unit Commitment with Large Scale Wind Farm）[D].北京：华北电力大学电气与电子工程学院（Beijing：School of Electrical and Electronic Engineering，North China Electric Power University），2011.

[8]艾欣，刘晓，孙翠英（Ai Xin，Liu Xiao，Sun Cuiying）. 含风电场电力系统机组组合的模糊机会约束决策模型（A fuzzy chance constrained decision model for unit commitment of power grid containing large-scale wind farm）[J].电网技术（Power System Technology），2011，35（12）：202-207.

[9]艾欣，刘晓（Ai Xin，Liu Xiao）.基于可信性理论的含风电场电力系统动态经济调度（Dynamic economic dispatch for wind farms integrated power system based on credibility theory）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（S）：12-18.

[10]刘晓（Liu Xiao）.新能源电力系统广域源荷互动调度模式理论研究（Theoretical Study on Wide Area Source and Load Interactive Scheduling Mode of New Energy Power System）[D].北京：华北电力大学电气与电子工程学院（Beijing：School of Electrical and Electronic Engineering，North China Electric Power University），2012.

[11]Liang Ruey-Hsun，Liao Jian-Hao.A fuzzy-optimization approach for generation scheduling with wind and solar energy systems[J]. IEEE Trans on Power Systems，2007，22（4）：1665-1674.

[12]Su Chung-Ching，Hsu Yuan-Yih.Fuzzy dynamic programming：an application to unit commitment[J].IEEE Trans on Power Systems，1991，6（3）：1231-1237.

[13]Miranda V，Pun Sio Hang. Economic dispatch model with fuzzy wind constraints and attitudes of dispatchers[J].IEEE Trans on Power Systems，2005，20（4）：2143-2145.

[14]熊虎，向铁元，陈红坤，等（Xiong Hu，Xiang Tieyuan，Chen Hongkun，et al）. 含大规模间歇式电源的模糊机会约束机组组合研究（Research of fuzzy chance constrained unit commitment containing large-scale intermittent power）[J].中国电机工程学报（Proceedings of the CSEE），2013，33（13）：36-44.

[15]丁晓东（Ding Xiaodong）.不确定系统优化理论与应用研究（A Study on Optimal Theory and Its Application For Uncertain Systems）[D].上海：东华大学信息科学与技术学院（Shanghai：College of Information Science and Technology，Donghua University），2002.

[16]刘宝碇，赵瑞清，王纲.不确定规划及应用[M].北京：清华大学出版社，2003.

[17]周玮，彭昱，孙辉，等（Zhou Wei，Peng Yu，Sun Hui，et al）.含风电场的电力系统动态经济调度（Dynamic economic dispatch in wind power integrated system）[J]. 中国电机工程学报（Proceedings of the CSEE），2009，29（25）：13-18.

[18]Attaviriyanupap P，Kita H，Tanaka E，et al. A hybrid EP and SQP for dynamic economic dispatch with nonsmooth fuel cost function[J].IEEE Trans on Power Systems，2002，17（2）：411-416.