基于B 样条函数的不良负荷数据改进辨识方法

唐文左，段 磊，王鹏举，颜 伟，赵 霞，余 娟

（1.重庆市电力公司电力科学研究院，重庆401123；2.输配电装备及系统安全与新技术国家重点实验室（重庆大学电气工程学院），重庆400044；3.山东滨州供电公司调度中心，滨州256610）

负荷数据是电力系统重要的基础数据之一，负荷数据的准确性直接影响电力系统计算、分析和决策的有效性。然而，由于仪表故障、通信错误、外界干扰、用电设备偶然故障停运以及其他未知原因，数据采集与监视控制系统SCADA（supervisory control and data acquisition）中的负荷数据往往含有不良数据，如何对不良数据进行有效辨识和校正成为基础数据分析和处理的一项重要任务[1-3]。

目前，针对电力系统中不良负荷数据辨识问题，现有研究主要是基于残差检测、神经网络、数据挖掘以及聚类分析的方法[3-10]。这些方法应用于不良负荷数据辨识时存在以下问题：①当历史负荷数据中不良数据比例较大时，大多数基于概率统计的辨识方法难以适用[3-5]；②由于负荷波动的不确定性或电力故障随机性，负荷数据可能出现较大偏移，以上方法很难准确判断其为不良负荷数据还是遵循一定增长趋势的正常数据[6-8]；③基于样本训练的神经网络方法难以处理小样本或参考样本缺失的中长期负荷曲线数据[9-10]。由于非参数估计的B 样条平滑方法在未知负荷曲线的函数形式和任何先验信息时都能近似逼近函数曲线，且在回归区间内具有较好的平滑效果和估计精度，文献[1]鉴于此提出了基于B 样条平滑的电力系统不良负荷数据辨识方法，并取得了较好的辨识效果。

然而，文献[1]所提方法存在一些问题：B 样条基函数是以所有历史负荷数据来形成节点向量，数据规模相对较大；受噪声的随机影响，基于曲率信息的单平滑项较难准确地拟合出原始曲线的所有形状特征，从而影响局部波动幅度较小的不良负荷数据辨识；直接以样条曲线拟合值作为不良负荷数据的校正值，校正精度有待提高。本文基于B 样条函数的不良数据辨识方法，提出了基于局部特征值点的节点向量形成方法以降低节点向量数据规模；同时引入了综合反映原始负荷曲线曲率和弧长信息的多平滑参数项，来准确反映负荷曲线的实际特征规律；最后提出了基于相似日负荷曲线聚类分析的不良数据校正方法。从而改善了不良负荷数据辨识及校正的精度和计算效率。

1 不良负荷数据的B 样条函数辨识原理

根据B 样条函数曲线的几何特性，任意自由型函数曲线y（t）都可表示成一系列相互独立的B样条基函数的线性加权组合形式，即

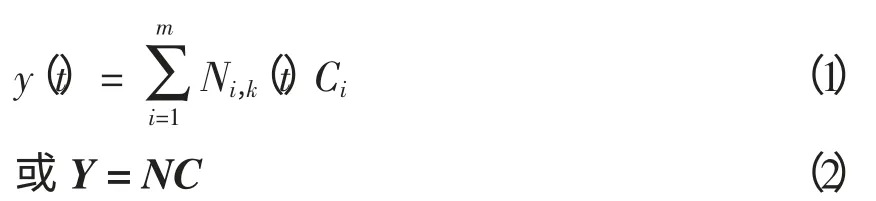
式（2）中，Y=[y（1），…，y（j），…，y（n）]T为自由型函数曲线的n 维向量形式；C=（C1，…，Ci，…，Cm）T为m 维的控制点向量；N 为n×m 维的B 样条基函数矩阵，即

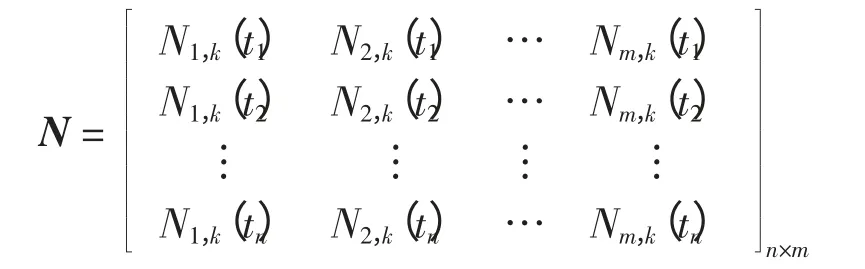
k 为样条函数的次数，本文中采用三次B 样条函数，即k=3。

B 样条曲线是由一系列相对独立的基底函数加权线性组合而构成。根据de Boor-Cox 递推公式[11]，B 样条基函数Ni，k可表示为

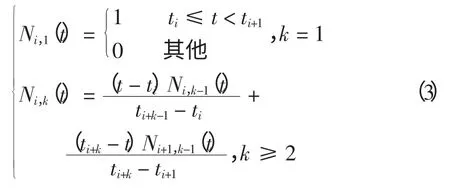
式中：k 为样条函数的次数；ti、ti+1、ti+k和ti+k-1都是节点向量T={tj|j=0，1，…，n+k+1}中的节点值。

节点向量T 是形成B 样条基函数的重要数据，以负荷曲线数据X={xi|i=1，2，…，n}为参考，利用积累弦长参数化法形成非递减实数序列为

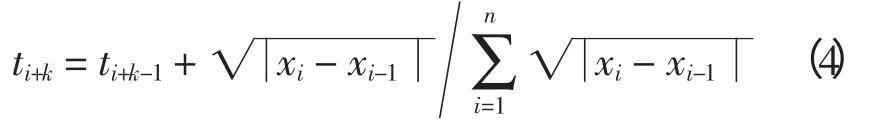
式中：i=1，2，…，n；设端节点重复度[11]为k+1，即令节点t0=t1=t2=t3=0，tn+k-2=tn+k-1=tn+k=tn+k+1=1。

引入平滑项SM（smoothing measure）[1]解决数据辨识中过度拟合问题，则将样条曲线平滑的目标函数定义为加权方差项，即

式中：σ2表示曲线拟合方差；λ 表示单平滑参数，最优的平滑参数取值现已有许多不同的准则[12-16]；SM 表示曲率平滑项，其计算表达式为

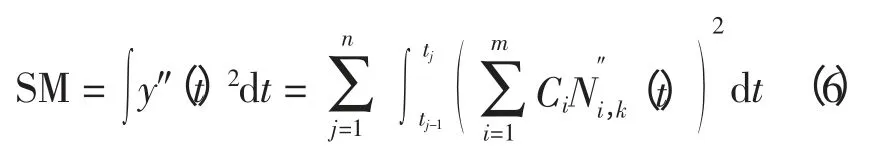
为书写方便，令m 阶方阵R 的元素R（i，j）为

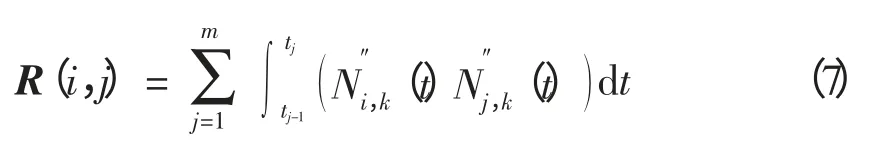
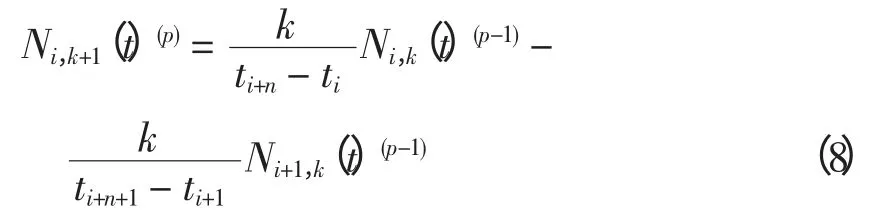
式中，p 表示B 样条基函数的微分阶数。

则曲率平滑项SM 可表示为

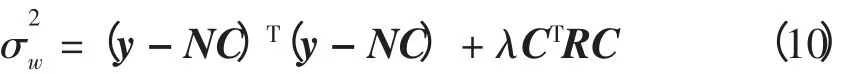
式中，y 为原始负荷曲线数据的n 维列向量形式。

根据最小二乘法，对式（10）求极值可以反算得到m 维的控制点向量为

则B 样条函数的拟合负荷曲线为

为了有效辨识出不良负荷数据，采用置信区间的判断方法[1]：若拟合数据位于置信区间范围内，则认为该样本数据是正确数据；否则为不良数据。定义ti时刻100*（1-α）%的置信区间为

式中：yi为原始负荷曲线y 的第i 个负荷值；n 为曲线的负荷点个数；σ2为曲线拟合方差为对角阵V 的第i 个对角元，且V=diag（S×ST×σ2）。

2 改进的B 样条函数辨识方法

研究发现，文献[1]方法仍存在以下问题：B 样条基函数是以所有的历史负荷数据来形成节点向量，数据规模较大；单平滑项在局部平滑逼近过程中曲线拟合灵敏度较低，影响局部波动幅度较小的不良负荷数据辨识；直接以样条曲线拟合值作为不良负荷数据的校正值，校正精度还有待提高。

为此，本文从以下方面提出改进方法：①提出了基于端点及局部极值点的节点向量选取策略；②引入了多平滑项和多平滑参数策略；③根据负荷曲线的周期性规律，提出了基于负荷曲线相似样本聚类的不良数据校正方法。

2.1 基于局部特征值点的节点向量选取策略

为减少大规模负荷数据的辨识时间，本文提出基于局部特征值点选取来构造节点向量的方法[17]。

给定数据序列X={xi|i=1，2，…，n}，定义序列中xi，i∈（1，n）为第i 个数据点在时间序列中的位置，xi为满足以下关系的数据记录：

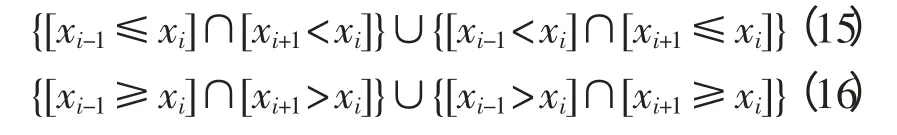
序列中在局部范围内小于其前后相邻两个序列点的数据点称为局部极小值点，大于其前后相邻两个序列点的数则称为局部极小值点。根据上述定义，序列中满足式（15）的数据点xi为局部极大值点，序列中满足式（16）数据点的为局部极小值点[11]。由于负荷曲线中的不良负荷数据是局部突变点，因此不良负荷数据点也一定是局部极值点。故提取负荷曲线中的局部极值点代替原始负荷数据点来构造节点向量，可大幅降低节点向量数据规模。

考虑到负荷曲线中不良负荷数据点大多为突变点，同时根据de Boor-Cox 公式，形成B 样条基函数的局部支撑区间需要足够多数据节点[11]，倘若只利用选取的极值点和端点形成节点向量，则不能完整体现不良负荷数据点前后相邻时刻的特征信息，从而抑制数据辨识的精度。因此，本文采用补充极值点前后相邻时刻数据的方法，即补充极值点前后2 个时刻的负荷数据，重叠时刻的数据按一次计算，若某极值点前后相邻时刻的负荷数据也是局部极值点，则无需再补充。

2.2 多平滑项的引入

为了提高样条函数辨识的灵敏度，基于能量最小化思想[18-19]，本文引入多平滑项，综合考虑负荷曲线的曲率信息与弧长信息，在样条拟合中将加权方差项表达成最小平方误差与曲线能量泛函的加和形式，即

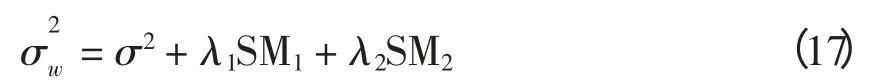
式中：SM1、SM2为引入的多平滑项，分别表示拟合负荷曲线的弧长信息和曲率信息，其数值的大小表明拟合曲线的光滑程度；λ1和λ2为对应的平滑参数。

引入多平滑项后，控制点向量为

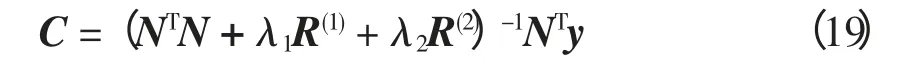
式中，R(1)和R(2)均为m 维方阵，其矩阵元素的具体计算公式为

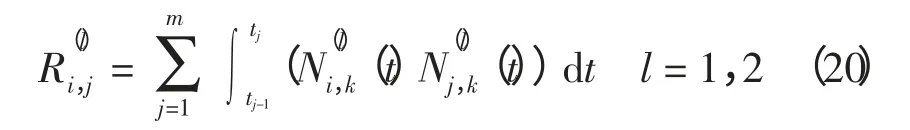
结合式（12）和式（19），样条拟合曲线数据为

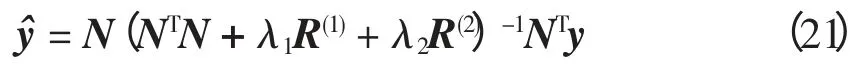
则此时n 维方阵S=N（NTN+λ1R(1)+λ2R(2)）-1NT。

2.3 多平滑参数的设定

为了控制平滑项的影响程度，需确定平滑参数。选择1 段正常负荷值作为训练数据，采用文献[1]中的增量训练算法，定义曲率平滑项的平滑参数λ2[1]为

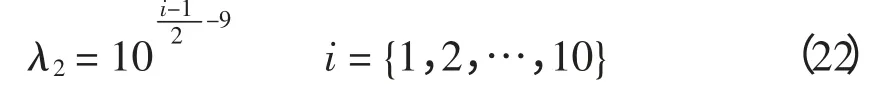
首先利用平滑参数λ2控制拟合样条曲线的整体形状特征，然后细调平滑参数λ1以增强曲线局部拟合效果。同理，将平滑参数λ1的调节范围也设置定义为10 个等级为

合理选取λ2、λ1值能调整拟合曲线平滑度与拟合度的平衡关系，以提高负荷曲线整体与局部的逼近效果：λ2的值越小，曲线的拟合度越高；λ1的值越大，曲线就越平滑[19]。因此在实际负荷曲线波动范围内合理选取λ1、λ2值，既能避免曲线过拟合，又能保证局部幅值波动较小的不良负荷数据的敏感度，有效提高负荷数据的辨识效果。

2.4 不良负荷数据的校正策略

根据电力系统负荷的日周期性，相似日间的负荷具有相似的负荷特征与模式[2]，本文提出通过负荷曲线相似样本聚类的方法对不良负荷数据进行校正。根据不良负荷数据所在日期，从SCADA历史数据库中提取其前后各一段时间的日负荷曲线进行负荷曲线的聚类分析[17]，具体步骤如下：

（1）对不良负荷数据进行预处理。首先剔除该不良负荷数据，并用其前后相邻时刻的负荷均值替代不良负荷数据值。

（2）标记不良负荷数据所在的日负荷曲线，构造日负荷曲线的样本集合，并计算任意两个样本之间的欧氏距离；

（3）利用日负荷曲线样本之间的欧氏距离，计算日负荷曲线之间的相似度并创建聚类；

（4）提取同类相似日负荷曲线中不良负荷数据点在相应时刻的负荷数据，并对不良负荷数据进行校正，其计算式为

式中：yi为同类相似日负荷曲线在不良负荷数据点对应时刻的负荷数据值；m 为同类相似日负荷曲线的样本个数；yr为不良负荷数据的校正值。

3 仿真与分析

3.1 算例描述

本文以重庆市某变电站的SCADA 系统所采集的负荷功率数据为基础，选取1#变压器在2008年1 月1 日至1 月30 日期间每天24 h 的有功功率实际数据（单位kW）进行仿真分析。该样本数据采样的时间间隔为1 h，共计720 个负荷数据点，则以采样点个数为横轴，绘制的实际负荷曲线如图1 中蓝色实线所示。

本算例中，取曲率平滑项参数λ2=10-8.5，弧长平滑项参数λ1=105λ2；选取置信水平α=0.05，则查表得Z1-α/2=1.96。

3.2 仿真结果及分析

图1 为本文方法形成节点向量时在原始负荷曲线上所选取的局部极值点（图1 中的圆形标记点）。

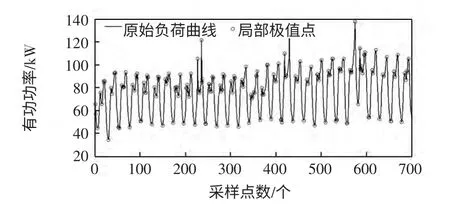
图1 原始负荷曲线的局部极值点Fig.1 Representative extreme points of original load curve

表1 给出了文献[1]方法和本文改进方法的不良负荷数据辨识对比结果。

表1 文献[1]与本文方法的辨识结果比较Tab.1 Comparison of bad load data identification result between proposed method and Re.[1]

由表1 及图1 可见，原始月负荷曲线（720 个负荷点）的局部极值点有184 个，根据第2.1 节所提节点向量形成策略，对局部极值点前后的负荷数据进行适当补充，形成428 个特征极值点，数据规模较原始负荷点数减少近40%，从而缩短了数据辨识的计算时间。

根据文献[1]方法和本文方法所得到的月负荷曲线不良数据辨识结果分别如图2 和图3 所示。

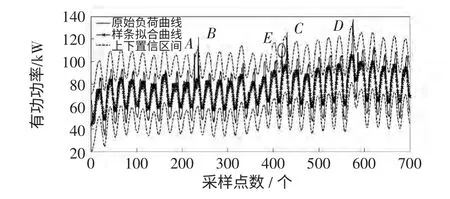
图2 文献[1]方法的辨识效果Fig.2 Effect of identification via the method in[1]

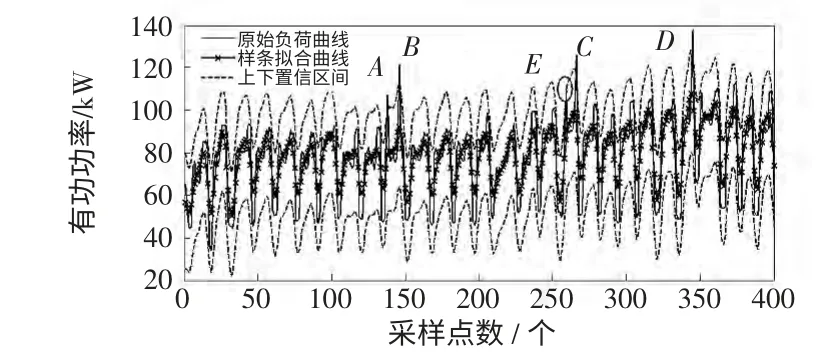
图3 本文改进方法的辨识效果Fig.3 Effect of identification via the improved method

由此可见，文献[1]方法以所有原始负荷数据点来形成B 样条基函数的节点向量，在单平滑项SM2作用下，辨识出4 处不良负荷数据，即图2 中A～D；本文采用基于局部特征值点的节点向量形成方法，引入综合曲率与弧长信息的多平滑项SM1、SM2，辨识出5 处不良负荷数据，如图3 中的A～E。显然，这两种方法对A～D 这4 个数据的辨识结果相同，而区别在于对E 点是否为不良数据的判定。

进一步分析E 点（即图4 中圆圈标注数据）这个数据：从横向上看，同一日负荷曲线中E 点（1 月18 日11：00，有功功率109.702 kW）前后相邻时刻点的负荷数据在84～94 kW 之间范围波动；从纵向上看，相邻日负荷曲线中在E 点相同时刻点的负荷数据在76～92 kW 范围内波动，显然E 点负荷不在该两组数据变化范围内，且同一日负荷曲线中E点相邻时刻的负荷数据的增减趋势平缓，即E 点负荷属于突变数据；但E 点负荷超出正常波动范围的幅值小于20%，因此E 点负荷可认为是波动幅度较小的不良负荷数据点。与文献[1]对比，本文中综合考虑曲线曲率和弧长信息的多平滑项参数方法不仅能够准确的辨识出负荷曲线中幅值突变的不良负荷数据点，而且极好地保持了对E 点这类幅值波动较小的不良负荷数据辨识的敏感度，增强了样条曲线在局部逼近过程中的曲线拟合灵敏性，提高了数据辨识的效果。

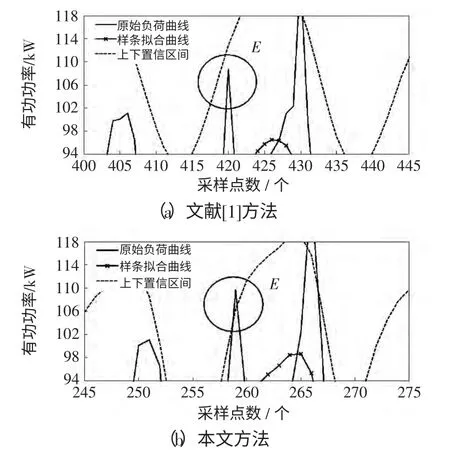
图4 两种方法E 点的辨识效果局部放大Fig.4 Identification effect of partial enlargement on point E via two methods

3.3 不良负荷数据校正结果及分析

采用第2.4 节方法，对辨识出的不良负荷数据进行校正。以C 点为例，通过聚类分析发现，C 点所在日负荷曲线（1 月18 日）的相似日为1 月21、22 和23 日（如图5 所示）。

图5 不良负荷数据C 点的相似日负荷曲线Fig.5 Similar daily load curves of bad load data C

表2 给出了不良负荷数据点的校正结果。从表2 的校正效果可知，相比于文献[1]的校正方法，本文的不良负荷数据校正的相对误差更小，且均小于1%。另外，针对本文改进方法所辨识出的不良负荷数据E 点，其校正后的负荷值与该时刻变压器实际运行情况中的真实值非常接近，从而也说明了本文方法具有更好的校正精度。

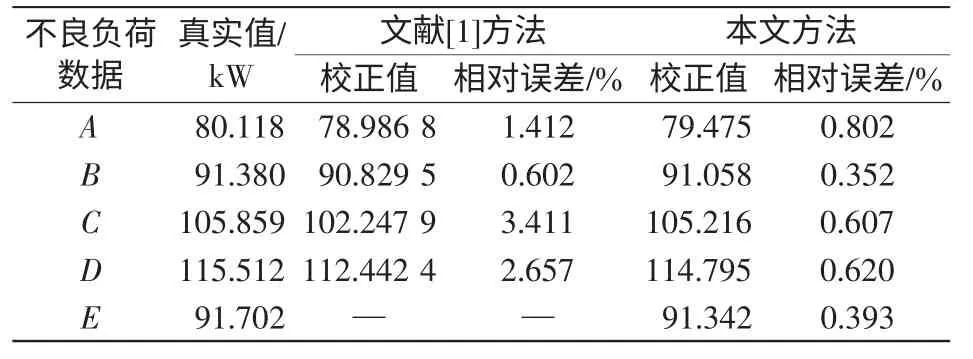
表2 两种方法的不良负荷数据校正效果Tab.2 Results of bad load data correction by two methods

4 结论

基于B 样条函数的不良数据辨识原理，本文提出了一种改进的不良负荷数据B 样条函数辨识方法。算例仿真结果表明，该方法主要有以下优点：

（1）采用基于局部特征值点的节点向量形成方法，可大幅降低节点向量规模，有效提高不良数据的辨识效率。

（2）引入同时反映负荷曲线曲率和弧长信息的多平滑项，对局部幅值波动较小的不良负荷数据具有良好的敏感度，提高了不良负荷数据辨识效果和准确性。

（3）提出基于日负荷曲线聚类的相似样本点均值的校正策略，更能反映原始曲线数据的变化趋势，校正精度更高。

[1]Chen Jiyi，Li Wenyuan，Lau A，et al.Automated load curve data cleansing in power systems[J]. IEEE Trans on Smart Grid，2010，1（2）：213-221.

[2]康重庆，夏清，刘梅.电力系统负荷预测[M].北京：中国电力出版社，2007.

[3]于尔铿. 电力系统状态估计[M]. 北京：水利电力出版社，1985.

[4]董丽娟，李晓明，肖鲲（Dong Lijuan，Li Xiaoming，Xiao Kun）. 电能量远程采集与分析系统的数据辨识与修正（Data distinguishing and data correcting in remote energy metering and analysing system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2002，14（3）：13-15，54.

[5]刘浩，崔巍（Liu Hao，Cui Wei）.R_N 检测与状态预估相结合的不良数据检测辨识法（The detection and identification method of bad data combined Rn detection and state forecast）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2001，13（2）：39-43.

[6]张晓星，程其云，周湶，等（Zhang Xiaoxing，Cheng Qiyun，Zhou Quan，et al）. 基于数据挖掘的电力负荷脏数据动态智能清洗（Dynamic intelligent cleaning for dirty electric load data based on data mining）[J].电力系统自动化（Automation of Electrical Power Systems），2005，29（8）：60-64.

[7]蒋雯倩，李欣然，钱军（Jiang Wenqian，Li Xinran，Qian Jun）. 改进FCM 算法及其在电力负荷坏数据处理的应用（Application of improved FCM algorithm in outlier processing of power load）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：1-5.

[8]孙国强，卫志农，周封伟（Sun Guoqiang，Wei Zhinong，Zhou Fengwei）. 改进迭代自组织数据分析法的不良数据辨识（The application of ISODATA to bad data detection and identification based on genetic algorithms）[J]. 中国电机工程学报（Proceedings of the CSEE），2006，26（11）：162-166.

[9]张国江，邱家驹，李继红（Zhang Guojiang，Qiu Jiaju，Li Jihong）. 基于人工神经网络的电力负荷坏数据辨识与调整（Outlier identification and justification based on neural network）[J].中国电机工程学报（Proceedings of the CSEE），2001，21（8）：104-107，113.

[10]陈泽淮，张尧，武志刚（Chen Zehuai，Zhang Yao，Wu Zhigang）.RBF 神经网络在中长期负荷预测中的应用（Application of RBF neural network in medium and long-term load forecasting）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（1）：15-19.

[11]施法中.计算机辅助几何设计与非均匀有理B 样条[M].北京：高等教育出版社，200l.

[12]De Boor C. A Practical Guide to Splines[M]. New York：Springer，2001.

[13]Hrdle W.Applied Nonparametric Regression[M]. London：Cambridge University，1990.

[14]吴喜之，王兆军.非参数统计方法[M].北京：高等教育出版社，1996.

[15]蒋大为，李安平（Jiang Dawei，Li Anping）.B 样条曲线的最小二乘保形光顺逼近（Shape preserving least-squares approximation by B-spline faired curves）[J].工程数学学报（Journal of Engineering Mathematics），2000，17（1）：125-128.

[16]梁锡坤（Liang Xikun）.B 样条类曲线曲面理论及其应用研究（Research on the Theory and the Application of Basic Spline Class Curves&Surfaces）[D].合肥：合肥工业大学计算机与信息学院（Hefei：Institute of Computer and Information Technology，Hefei University of Tech -nology），2003.

[17]王鹏举（Wang Pengju）.基于样条与核密度函数的不良负荷数据辨识方法研究（Research of Load Curve Data Cleaning Based on Spline and Kernel Function）[D].重庆：重庆大学电气工程学院（Chongqing：College of Electrical Engineering，Chongqing University），2012.

[18]原庆红，韩燮（Yuan Qinghong，Han Xie）.基于能量最小化控制点的B 样条插值算法（B-spline interpolation algorithm based on energy minimization control point）[J].微电子学与计算机（Microelectronics & Computer），2011，28（4）：49-56.

[19]罗卫兰（Luo Weilan）.B 样条曲线的光顺（B-spline Curve Fairing）[D].杭州：浙江大学理学院（Hangzhou：College of Science，Zhejiang University），2003.