基于CompactDAQ刚柔耦合动力学实验台的搭建*
武泽 余征跃 洪嘉振
(上海交通大学工程力学系,上海 200240)
引言
在机械制造、航空航天等众多领域中,刚柔耦合动力学问题都是研究热点.国内外许多学者都针对该问题展开了大量的理论研究工作.从针对小变形问题的混合坐标法[1],到大变形问题的绝对节点坐标法[2].洪嘉振利用哈密顿原理和速度变分原理建立了一次近似理论的动力学方程[3].章定国在考虑柔性梁横向弯曲变形以及纵向伸长变形以及非线性耦合变形项,利用第二类Lagrange方程建立了一次刚柔耦合动力学方程[4].
然而,同刚柔耦合问题在理论方面的发展相比,针对理论模型的验证实验还十分有限.杨辉等利用气浮台验证了动力刚化理论和一次近似理论[5].Yoo等利用高数摄像机验证了旋转柔性梁的动力学模型[6].刘锦阳等利用运动测量仪验证了基于非线性应变和位移的关系用绝对坐标法建立的几何非线性动力学模型[7].目前,鲜有针对刚柔耦合动力学问题的实验研究主要是因为伴随大范围运动的同时需要测量柔性体的变形,以及需要尽量减少阻尼对于实验的影响[8].搭建符合上述要求的实验台和相关测量组件造价成本高、开发周期长、适用性较差造成的.本文针对上述问题,研制了一款实验台,可针对不同模型采集数据验证理论.
气浮台依靠压缩空气在台体与轴承基座之间形成的极薄气膜,使气浮台整体浮起,从而实现模拟近似无摩擦的相对运动,可以用来模拟卫星在太空中真空环境下基本不受到干扰力矩的力学环境[9].目前,由于受到重力的影响,三轴气浮台不能直接进行带有柔性附件的刚柔耦合实验[10].近年来,在引进国外气浮台的基础上,国内一些院校以及研究所,如502所、西北工业大学、哈尔滨工业大学和国防科技大学等对气浮台的一些性能和用途进行过研究,主要用于实际的卫星仿真试验,哈尔滨工业大学也已研制出多自由度的气浮仿真设备[11].目前,气浮台全物理仿真技术的应用范围还是比较窄,国内更是如此.一方面,因为其技术缜密,价格高昂,使得一些实验无法应用.另一方面,除工业自动化和航空之外,在其它领域开展应用气浮台的研究较少,只有进行基础研究才涉及到.刚柔耦合动力学是少数可以利用气浮台进行实验的研究领域.
CompactDAQ控制器(下称cDAQ)是NI公司推出的一类嵌入式控制、测量应用的处理器,将连接性与信号调节集成在I/O模块中,可以直接对接任何传感器或信号.使用cDAQ控制器和LabVIEW软件可以设计数据采集、分析、显示和管理的系统.
本文在气浮台的基础上,利用cDAQ控制器和数字I/O模块,搭建了适合进行刚柔耦合实验的实验台,该实验台具有低成本、高精度、高可靠性、扩展灵活等特点.
1 实验台的工作原理
刚柔耦合实验台依靠压缩空气在台体与轴承基座之间形成的极薄气膜,使气浮台整体浮起,从而实现模拟近似无摩擦的相对运动.止推轴承限制了实验台的两个水平移动方向自由度、一个垂直方向自由度和两个转动方向自由度,因此可认为气浮轴承使实验台只能绕铅直轴旋转.整个实验装置可简化为中心刚体-柔性梁模型,进行相关的刚柔耦合实验.
从结构上说,实验台系统大致可以分为实验台气浮装置、中心刚体、柔性梁和测量控制的传感器控制器,如图1,2所示.
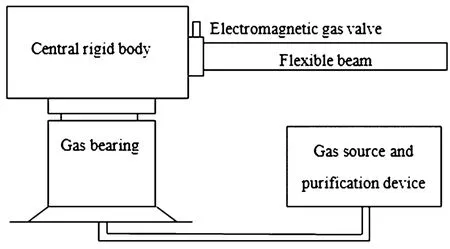
图1 刚柔耦合实验台示意图Fig.1 Schematic diagram of the rigid-flexible coupling experiment table Nitrogen cylinder
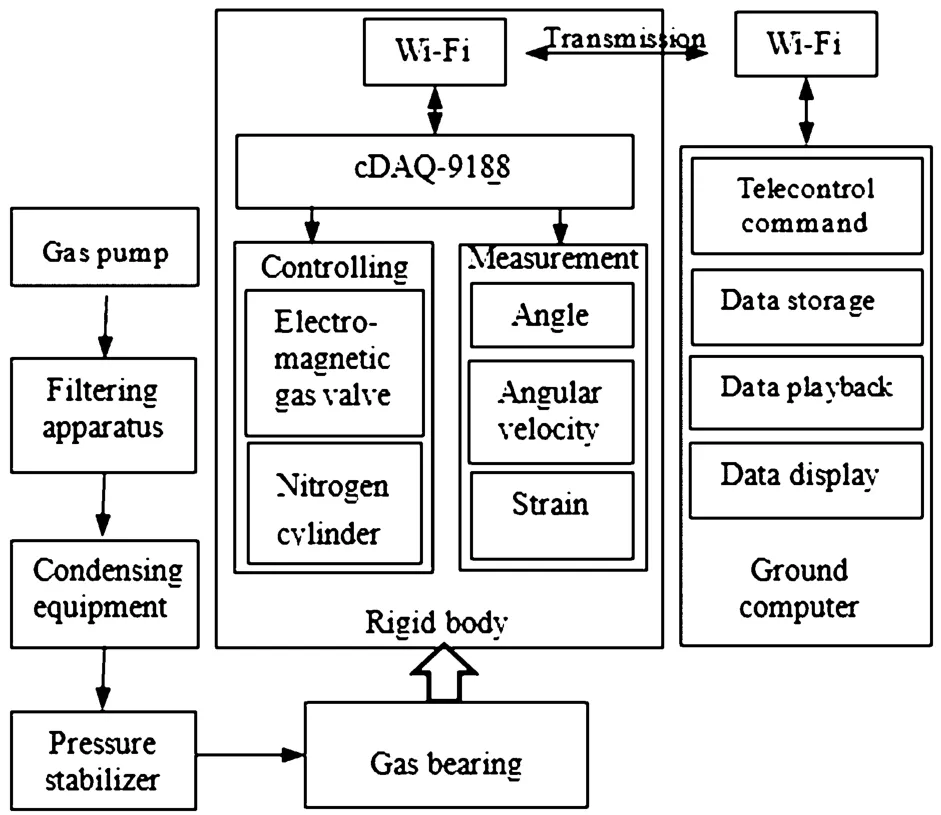
图2 刚柔耦合实验台工作原理图Fig.2 Functional diagram of the rigid-flexible coupling experiment table
2 实验台的硬件设计
实验台需要对中心刚体转动的角位移、角速度,柔性梁的应变进行测量,同时控制电磁喷气阀的喷气.首先通过相应的传感器将测量或控制的信号转化为模拟量、数字量、开关量.通过相应模块传输到cDAQ控制器.测量控制系统的硬件部分如图3所示.

图3 CompactDAQ测量与控制系统硬件配置Fig.3 Hardware configuration of the CompactDAQ measurement and control system
2.1 角位移
中心刚体的角位移采用英诺伺服Maglin系列磁栅角位移编码器测量,磁栅尺长980mm,13细分,将其贴合在气浮台基座圆周上,磁栅感应器固定在旋转台上,从而实现相对角位移的测量.按照RS-422A标准输出数字正交编码器信号,单圈分辨率在四倍频细分后为1605632脉冲,折合角度分辨率为2.24×10-4°.9401双向数字模块可接收编码器测得的信号,9401双向数字模块是一款8通道、100ns的双向数字输入模块.
2.2 角速度
中心刚体的角速度采用西安中星测控的CSARS-02角速率陀螺仪来测量,测量范围可达到±360°/s,分辨率为0.15°/s.陀螺仪输出的电压信号通过9234电压测量模块接收.9234电压测量模块是4通道动态采集设备,具有24位分辨率,采样速率可达51.2kS/s.
2.3 应变
用应变片来测量柔性梁的变形是一种被广泛采用的方法.将应变片贴在被柔性梁上,应变片会随着柔性梁的应变一起伸缩,这样里面的金属箔材就随着应变伸长或缩短.通过9237同步应变模块测量柔性梁的应变.9237同步应变模块是具有四个模拟输入通道24位同步电桥设备,有24位分辨率,采样速率可达50kS/s.
2.4 电磁喷气阀
电磁喷气阀可用于对中心刚体转动的控制,内含电磁继电元件,当输入电压到达阈值,就会喷出氮气瓶中的氮气,使实验台转动.9472数字输出模块是一款8通道100μs的源极数字输出模块.每条通道都兼容6~30V信号,用于控制电磁喷气阀的输入电压.
2.5 数据传输方式
实验台上的cDAQ控制器通过TP-LINK无线路由器与地面计算机按IEEE 802.11n协议实现测量数据、遥控指令的无线传输.传输速率最高可达150Mbps,在检测到周边有无线信号干扰时,可自动调整频宽模式,避开信道干扰,使无线传输更加稳定.
2.6 刚柔耦合实验台基本参数指标
中心刚体有效的加载质量约为100kg.中心刚体的转动惯量约为12.92kg·m2.刚柔耦合实验台最终干扰力矩小于8×10-4N·m.
柔性梁的尺寸为1800mm×100mm×2.5mm,材质为铝,弹性模量E=6.9×1010N/m2,密度ρ=2766.7kg/m3,前三阶约束固有频率为0.62Hz、3.82Hz、10.72Hz.
气瓶总容积为16升.小喷气推力系统两个,大喷气推力系统一个.喷气最小脉冲宽度30ms.喷气大推力大于1N,小推力大于0.33N.喷气力矩在0.098N·m-0.279N·m范围可调.喷气延迟时间小于8ms.
3 实验台的软件设计
刚柔耦合动力学实验台不仅具有测量角位移、角速度、应变、控制电磁喷气阀的功能,同时还可以将测量的数据输出.
地面计算机是上位机处理器,负责完成人机交互、控制下位机运行状态和复杂数据处理等.为了避免连线电缆对于实验台运动的影响,cDAQ控制器与地面计算机的通讯方式采用无线路由器,在每次进行实验前,需打开实验台上的电源,将地面计算机连接到该无线路由器的网络上.
3.1 子程序框图
利用实验台进行刚柔耦合实验,写出实现前文所述功能的子程序.子程序的框图如图4、图5所示.
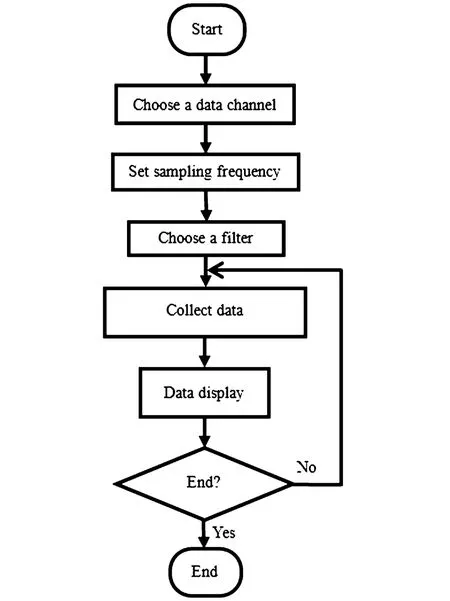
图4 测量程序框图Fig.4 Diagram of measurement
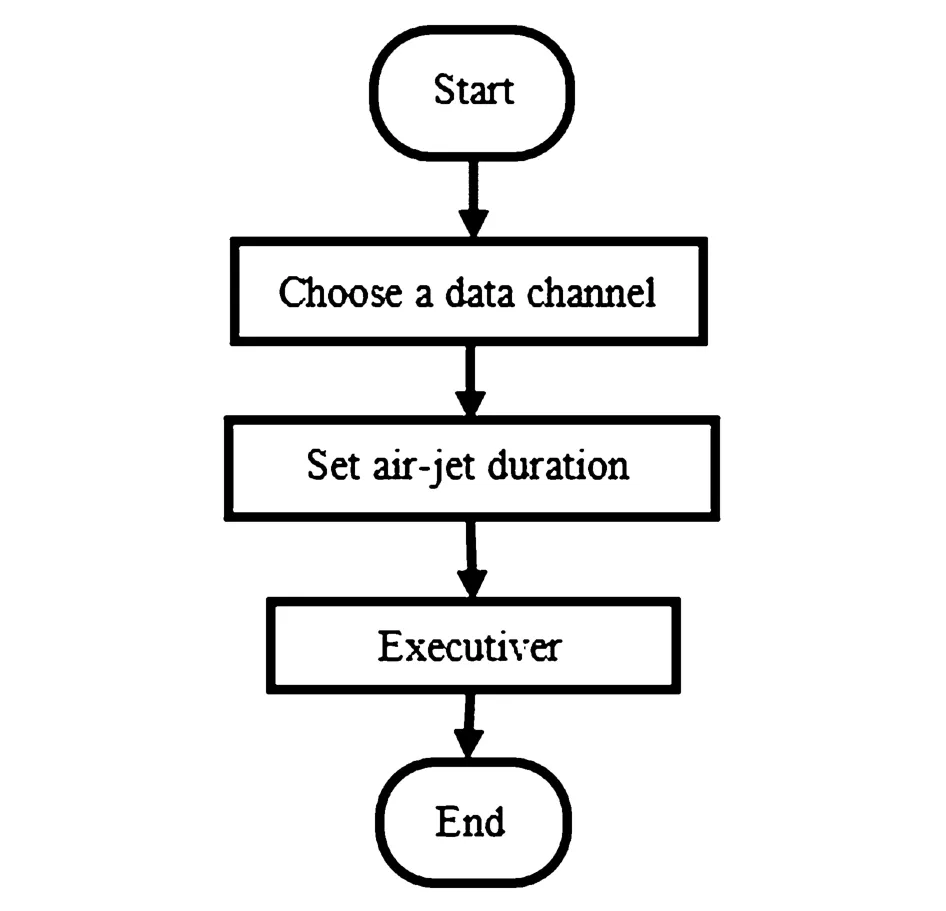
图5 电磁喷气阀的控制程序框图Fig.5 Lock diagram of controlling electromagnetic gas
3.2 刚柔耦合实验台实验程序
实验程序有如下功能:角位移的测量、角速度的测量、电磁喷气阀的控制、测量数据的输出.利用LabVIEW编程软件通过把不同的采集任务组集在一个程序中,各个任务会独立运行,利用数据输出模块可以将测量的各种物理量输出.程序界面如图6所示.
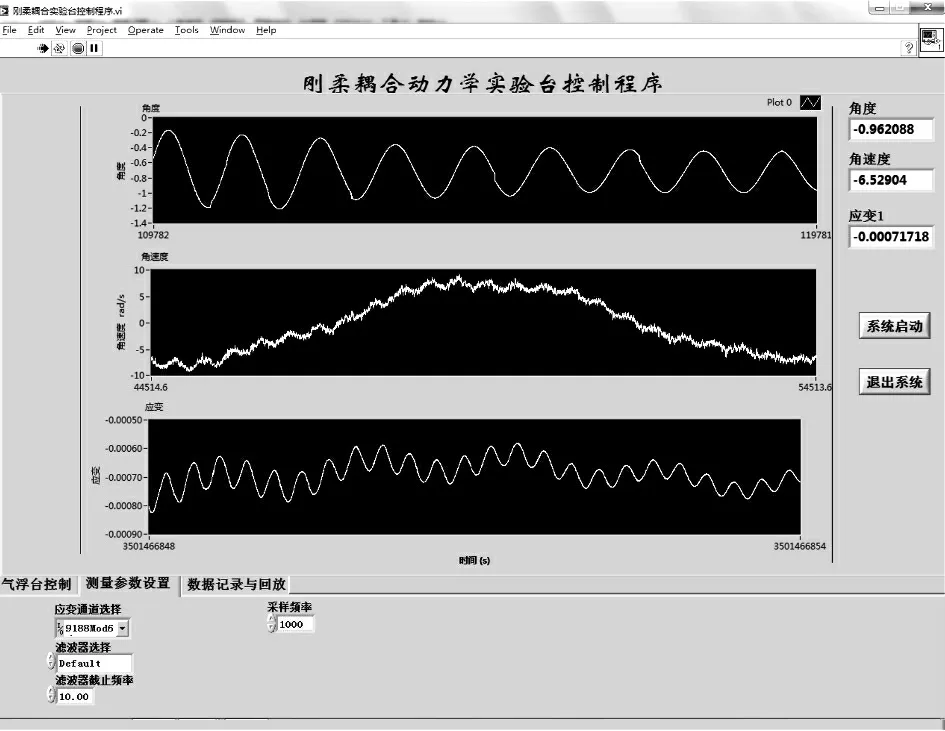
图6 刚柔耦合实验台程序界面Fig.6 Interface of the rigid-flexible coupling experiment table
3.3 控制程序的编写
通过上述功能模块,实验台可以完成一系列的测量功能,还可以将不同的控制方法通过Lab-VIEW编程嵌入本系统程序中,实现对不同刚柔耦合系统控制方法的验证.
利用测量得到的实验台角位移和角速度,通过嵌入的控制算法计算,使得电磁喷气阀动作来执行相应的喷气,以实现实验台大范围的转动.
控制算法可以利用LabVIEW中的MathScript Node模块嵌入到整个程序之中.MathScript Node模块是基于matlab相关编程语言的模块,在完成控制算法的仿真之后,可直接将控制程序的m文件嵌入其中就可以进行控制实验.
4 中心刚体—柔性梁的刚柔耦合实验
实验采用的模型为中心刚体—柔性梁模型,中心刚体转动惯量为12.92kg·m2,柔性梁固接在中心刚体的铝合金框架上,安装点距离中心转轴为100cm,柔性梁的尺寸为1800mm×100mm×2.5mm,材质为铝,弹性模量E=6.9×1010N/m2,密度ρ=2766.7kg/m3,在距离柔性梁固支端60cm处正反两面各粘贴一个应变片,半桥接线,用于测量柔性板的应变.
分别在下面四种不同的工况下,敲击柔性板距离固支端100cm处激发柔性板振动,采集柔性梁的应变和中心刚体的角位移,利用快速傅立叶变换对测量数据进行频谱分析,其工况为:
(1)当实验台没有浮起保持静止时,采集柔性梁的应变;
(2)将实验台浮起使之可以自由转动,同时采集柔性梁的应变和中心刚体的角位移;
(3)在台体和基座之间对称安装有四组线性弹簧,在台体小幅转动的情形下可用来模拟线性扭转弹簧,同时采集柔性梁的应变和中心刚体的角位移;
(4)更换一组刚度更大的弹簧,同时采集柔性梁的应变和中心刚体的角位移.
其实验结果如图7、图8所示.
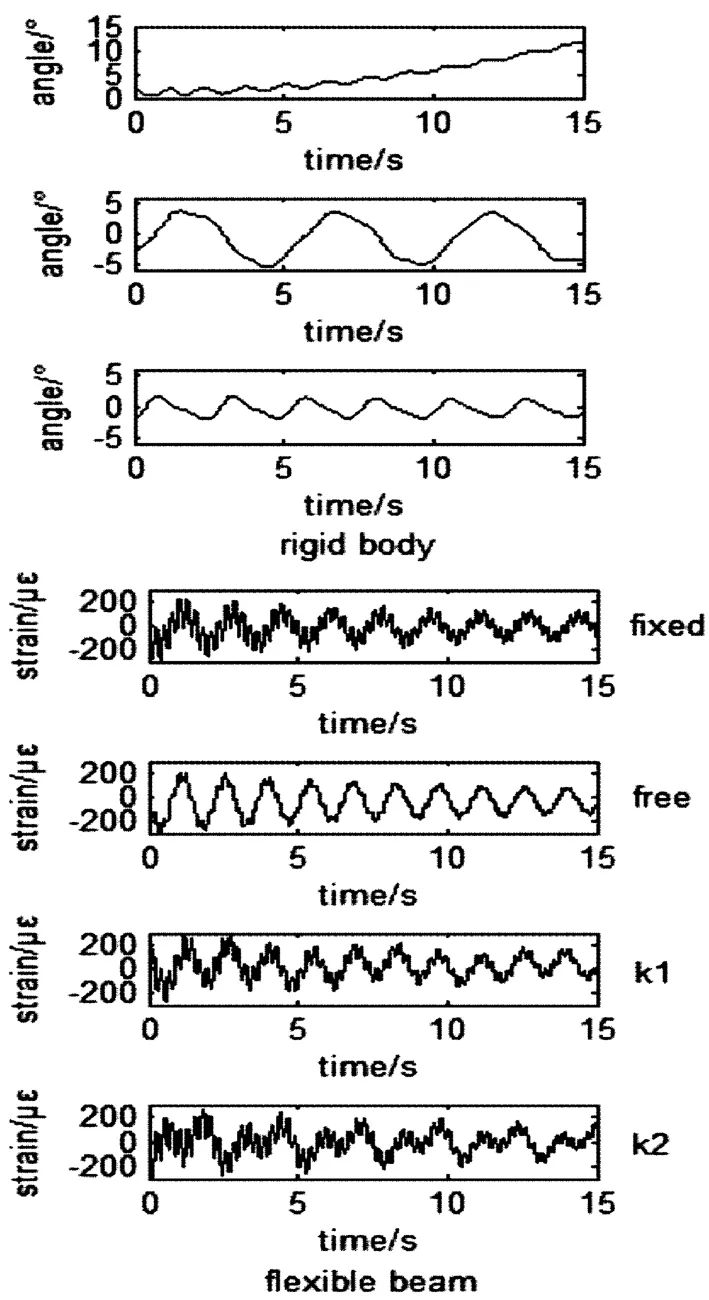
7 不同工况下中心刚体和柔性梁响应时域曲线Fig.7 Time-domain curve of rigid body and flexible beam under different conditions

表1 不同工况下中心刚体和柔性梁的频率Table 1 Frequency of rigid body and flexible beam under different conditions
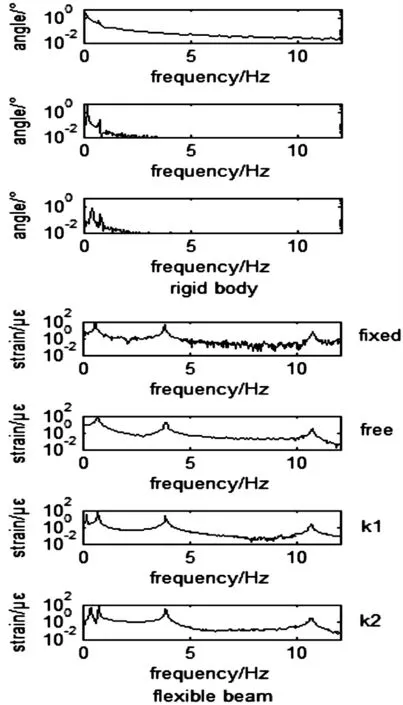
8 不同工况下中心刚体和柔性梁响应频谱曲线Fig.8 Frequency spectrum of rigid body and flexible beam under different conditions
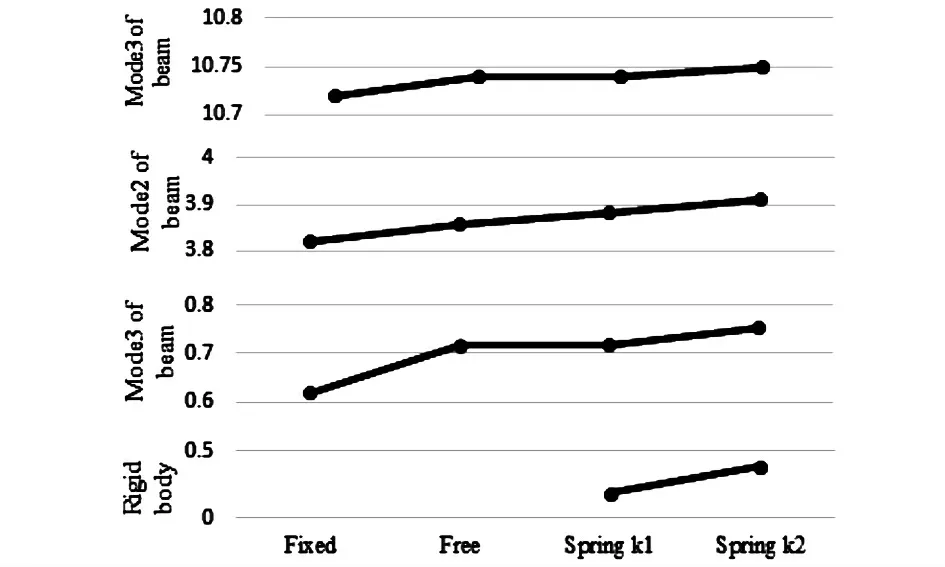
图9 不同工况下中心刚体和柔性梁的固有频率比较图Fig.9 Comparison of frequency of rigid body and flexible beam under different conditions
表1记录了不同工况下中心刚体和柔性梁的各阶频率,其中弹簧k1与弹簧k2的等效刚度分别为26.51N·m/rad和128.71N·m/rad.在自由状态下,中心刚体的运动响应包括两部分,一部分是中心刚体的刚体运动,另一部分是由于柔性梁的自由振动引起的运动,柔性梁的运动均是由于自身振动引起的;在附加弹簧状态下,中心刚体的运动响应包括两部分,一部分是中心刚体与弹簧组成的振子系统,另一部分是由于柔性梁的振动引起的运动.中心刚体运动基本上只受梁一阶频率的影响.随着工况的改变,柔性梁的前三阶固有频率和中心刚体的运动频率依次上升,如图9所示.
5 结论
本文在气浮台的基础上,基于CompactDAQ控制器和一系列数字I/O模块搭建了刚柔耦合实验台的硬件部分,同时利用LabVIEW编程语言实现了测量与控制的功能,通过实验台完成了中心刚体—柔性梁的刚柔耦合系统实验.该实验台具有高可靠性、低成本、扩展灵活的优点,可按照设定的参数采集角位移、角速度、应变等物理量,同时还可以验证不同控制方法对于刚柔耦合系统控制的效果.
1 Meirovitch L.Hybrid state equations of motion for flexible bodies in terms of quasi-coordinates.Journal of Guidance,Control,and Dynamics,1991,14(5):1008~1013
2 Mikkola A M,Matikainen M K.Development of elastic forces for a large deformation plate element based on the absolute nodal coordinate formulation.Journal of Computational and Nonlinear Dynamics,2006,1(2):103~108
3 Liu J Y,Hong J Z.Dynamic modeling and modal truncation approach for a high-speed rotating elastic beam.Archive of Applied Mechanics,2002,72(8):554~563
4 Chen SJ,Zhang D G.Dynamic modeling and analysis of hub-tapered beam system.Advances in Mechanical Engineering,2013:313279
5 杨辉,洪嘉振,余征跃.刚柔耦合建模理论的实验验证.力学学报,2003,35(2):253~256(Yang H,Hong J Z,Yu Z Y.Experiment validation on modeling theory for rigid-flexible coupling systems.ACTA Mechanica Sinica,2003,35(2):253~256(in Chinese))
6 Yoo WS,Kim M S,Mun SH,Sohn JH.Developments of multibody system dynamics.Computer Simulations and Experiments,Multibody System Dynamics,2007,18(1):35~58
7 刘锦阳,邹凡,余征跃.气浮台—薄板刚—柔耦合系统动力学建模和实验研究.振动与冲击,2012,31(21):11~14(Liu J Y,Zou F,Yu Z Y.Dynamic modeling and tests for a hub-plate rigid-flexible coupled system.Journal of Vibration and Shock,2012,31(21):11~14(in Chinese))
8 杨辉,洪嘉振,余征跃.柔性多体系统动力学实验研究综述.力学进展,1900,34(2):171~181(Yang H,Hong J Z,Yu Z Y.Survey of experiments for dynamics of flexible multibody system.Advances in Mechanics,1900,34(2):171~181(in Chinese))
9 李季苏,牟小刚,张锦江.卫星控制系统全物理仿真.航天控制,2004,22(3):37~41(Li JS,Mu X G,Zhang J J.Physical simulation for satellite control systems.Aerospace Control,2004,22(3):37~41(in Chinese))
10 陈欢龙,周军,刘莹莹等.三轴气浮台多体动力学建模与仿真.西北工业大学学报,2010,28(3):332~337(Chen H L,Zhou J,Liu Y Y,Mu X G.Dynamics modeling of three-axis air-bearing table with rotatable appendages.Journal of Northwestern Polytechnical University,2010,28(3):332~337(in Chinese))
11 许剑,杨庆俊,包钢等.多自由度气浮仿真试验台的研究与发展.航天控制,2009,27(6):96~101(Xu J,Yang Q J,Bao G,et al.Research and development of air bearing spacecraft simulator on the multiple degrees of freedom.Aerospace Control,2009,27(6):96~101(in Chinese ))

