预应力巨型支撑-钢框架结构的Pushover分析
张福星,郭君渊,王 祎,唐柏鉴
(江苏科技大学土木工程与建筑学院,江苏镇江212003)
预应力巨型支撑-钢框架结构(简称PMBFS)在2009年由唐柏鉴等人[1-2]提出.该结构将预应力拉索引入普通钢框架中并参与抵抗水平荷载,旨在提高钢框架的抗侧刚度,克服钢框架-支撑结构的节点复杂性,降低用钢量.
文中采用Pushover分析方法,选取两种具有代表性的水平荷载加载模式,对结构施加单调递增的水平荷载,逐步将结构推至一个预定的状态来分析其非线性性能.
1 数值分析模型
采用一榀经过抗风抗震设计的15层4跨PMBFS结构为分析模型(图1),每5层设置X型预应力巨型支撑.层高为3.6 m,每跨跨度为6 m.钢梁钢柱采用Q345B钢材,弹性模量为206 GPa,线膨胀系数为 1.2 ×10-5,密度为 7 850 kg/m3.预应力拉索抗拉强度为1 670 MPa,弹性模量为1.95×105,线膨胀系数为 1.32 ×10-5,拉索为理想柔索,满足胡克定律.构件尺寸见表1,2.
竖向荷载:恒荷载4.5 kN·m-2,活荷载2.5 kN·m-2.
风荷载:基本风压ω0=0.4 kN/m2,方向向右.
地震作用:按8度抗震设防(0.2 g),地震分组为第一组,建筑场地类别为II类场地.
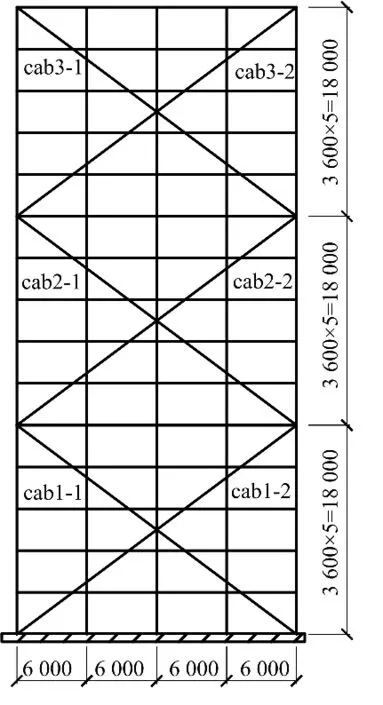
图1 预应力巨型支撑-钢框架结构(单位:mm)Fig.1 Pre-stress-mega-braced steel framestructure(unit:mm)
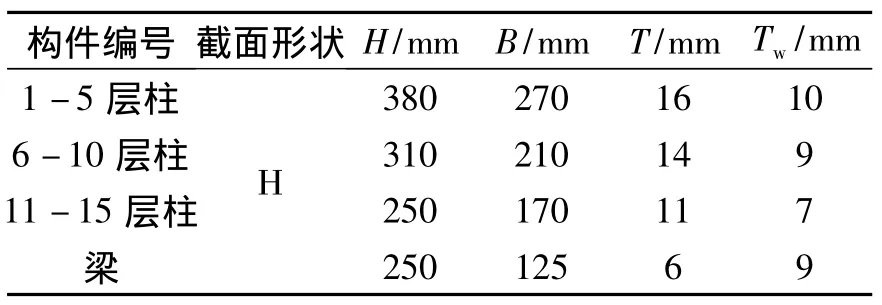
?
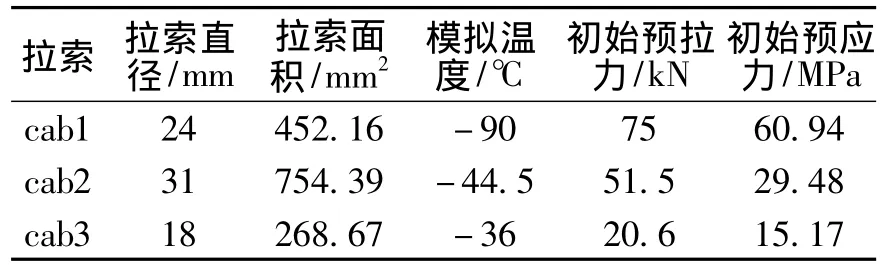
表2 拉索的直径和预拉力Table 2 Diameter and pretension of cable
2 Pushover分析
2.1 塑性铰理论模型及选择依据
采用SAP2000进行静载和推覆分析.带塑性铰的框架柱和框架梁单元简化模型如图2a),对框架而言,梁和柱的两端受力均比较大,梁的两端一般设置弯矩铰和剪力铰(离散铰);柱两端塑性铰位置处,轴力和弯矩相互作用,要考虑塑性铰的耦合作用,一般设置PMM相关铰.对预应力拉索在中间设置轴力铰(P 铰),塑性铰类型均选择 FEMA 型[3-8].

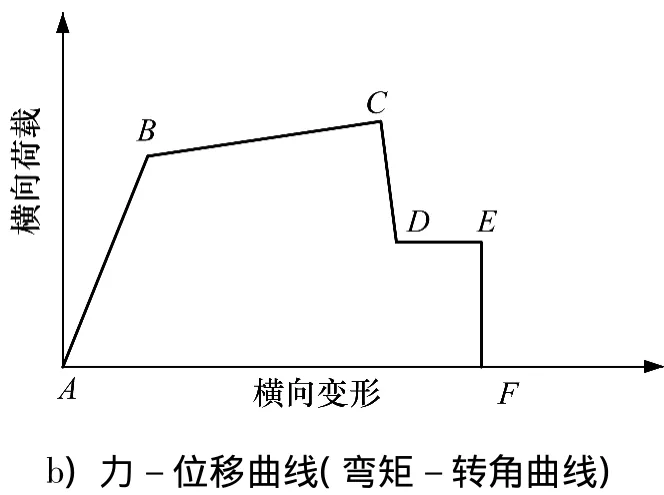
图2 塑性铰理论模型Fig.2 Theoretical model of plastic hinges
塑性铰力学模型如图2b),点B代表铰的屈服,AB段铰内没有变形发生(铰屈服前被假定为刚性的).当铰达到C点时,开始失去承载力,D点表示铰的残余强度,E点表示铰完全失效[9].
2.2 底部剪力和抗侧刚度
该体系底部剪力(τ)和抗侧刚度随顶点位移变化(S)的曲线如图3.
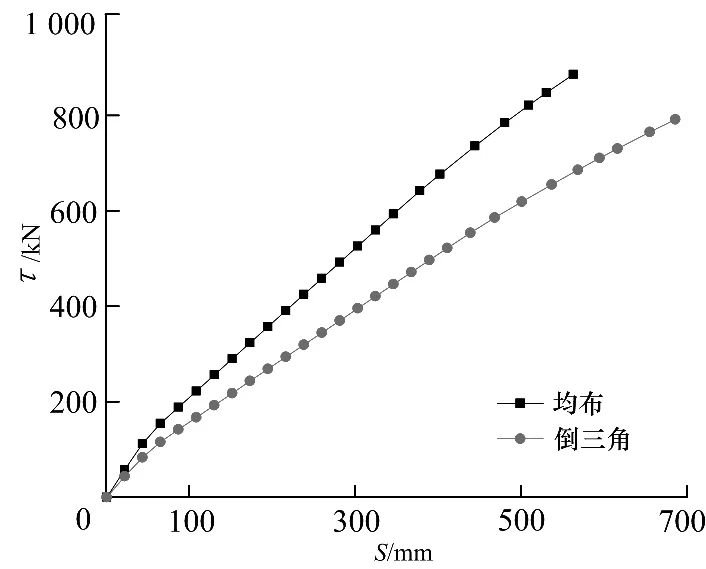
图3 底部剪力顶点位移关系曲线Fig.3 Base shear and lateral stiffness curve
由图3可知,随着水平荷载的增加结构逐渐由弹性状态过渡到弹塑性状态,底部剪力-顶点位移曲线由直线变化为曲线,且曲线斜率逐渐减小,最后当水平荷载达到极限值时,结构因出现大量塑性铰而达到承载力极限状态.倒三角分布模式下结构的极限荷载要小于均匀分布模式下结构的极限荷载.
2.3 结构破坏模式
2.3.1 均匀分布
如图4,均匀分布模式下,当水平荷载达到641.588kN时,第一大层内的框架梁首先开始屈服,结构的顶点位移为378.254mm;当水平荷载达到784.423kN时,结构第一大层内的框架柱开始出现塑性铰,此时顶点位移为480.68mm;当水平荷载达到极限荷载885.901kN时,结构破坏,顶点位移达到563.156mm,底层拉索开始出现塑性铰.

图4 均匀分布模式下塑性铰出现过程Fig.4 Plastic hinge of PMBFS under the uniformly horizontal load
2.3.2 倒三角分布
如图5,倒三角分布模式下,当水平荷载达到522.11kN时,第一大层内的框架梁首先开始屈服,结构的顶点位移为411.199mm;当水平荷载达到585.688kN时,结构第三大层内的框架柱开始出现塑性铰,此时顶点位移为468.468mm;当水平荷载达到极限荷载791.106kN时,结构破坏,顶点位移达到686.064mm,底层拉索开始出现塑性铰.

图5 倒三角分布模式下塑性铰出现过程Fig.5 Plastic hinge of PMBFS under the inverted triangular horizontal load
可见,在结构达到极限状态时,均匀分布模式比倒三角分布模式出现破坏的楼层相对要低一点.同时,在不同的水平加载模式下,虽然会得到不同的底部剪力-顶点位移曲线和不同的抗侧刚度以及水平极限荷载,但是得到的结构破坏模式基本相同.
2.4 抗震性能评估
多遇地震下结构体系的阻尼比取0.03,罕遇地震下阻尼比取0.05.
2.4.1 8度多遇地震
由图6可知,8度多遇地震下,结构未出现塑性铰,此时结构的底部剪力为117.936 kN,对应的顶点位移为67.518mm.
8度多遇地震作用时结构体系的层间位移角如图7,可见,层间位移角小于《建筑抗震设计规范》(GB 50011-2011)规定的限值1/250.

图6 两种水平荷载模式下8度多遇地震时的结构性能状态Fig.6 Structural performance point of 8 degrees multiple case earthquake under two kinds of horizontal loads

图7 8度多遇地震作用时的层间位移角Fig.7 Story drift angle of 8 degrees multiple case earthquake
2.4.2 8度罕遇地震
由图8可知,两种加载模式下,经过抗风抗震设计的PMBFS结构体系,其底层框架梁都开始进入弹塑性状态.
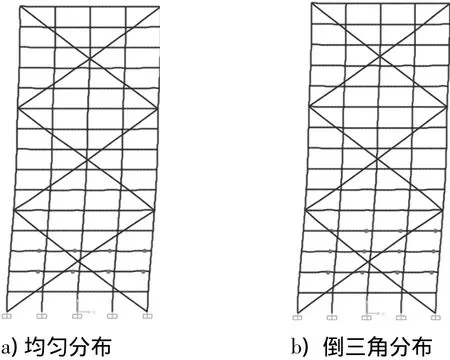
图8 两种水平荷载模式下8度罕遇地震时的结构性能Fig.8 Structural performance of 8 degrees rare case earthquake under two kinds of horizontal loads
8度罕遇地震作用时结构体系的层间位移角如图9,可见层间位移角小于《建筑抗震设计规范》(GB 50011-2011)规定限值1/50.
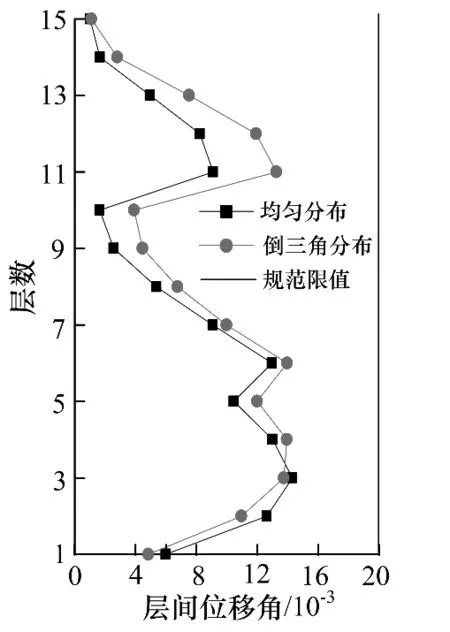
图9 8度罕遇地震作用时的层间位移角Fig.9 Story drift angle of 8 degrees rare case earthquake
3 结论
1)结构在均布模式下的极限荷载比倒三角模式下的大.
2)两种水平荷载模式下,结构破坏模式相似,首先是下部楼层梁屈服,当较多水平梁屈服后柱出现屈服,极限状态时拉索才会出现屈服.
3)经过抗风抗震弹性设计的预应力巨型支撑-钢框架结构,弹塑性抗震性能满足规范要求.
References)
[1] 唐柏鉴,顾盛.预应力巨型支撑-钢框架结构侧移模式研究[J].建筑科学,2010,26(9):57-61.Tang Baijian,Gu Sheng.Displacement mode of prestress-mega-braced steel frame structures[J].Building Science,2010,26(9):57 -61.(in Chinese)
[2] 唐柏鉴,顾盛.预应力巨型支撑-钢框架结构初始预拉力取值准则[J].沈阳建筑大学学报:自然科学版,2010,26(3):480-484.Tang Baijian,Gu Sheng.Rule of initial presress in prestress-mega-braced steel frame structure[J].Journal of Shenyang Jianzhu University:Natural Science,2010,26(3):480-484.(in Chinese)
[3] Helmut Krawinkler,Senerviratna G D P K.Pros and cons of a pushover analysis of seismic performance evaluation[J].Engineering Structures,1998,20:452 -464.
[4] 杨溥,李英民,王亚勇,等.结构静力弹塑性分析(pushover)方法的改进[J].建筑结构报,2000,21(1):44 -51.Yang Pu,Li Yingmin,Wang Yayong,et al.A study on improvement of push-over analysis[J].Journal of Building Structures,2000,21(1):44 -51.(in Chinese)
[5] Mwafy A M,Elnaashai A S.Static pushover versus dynamic collapse analysis of RC buildings[J].Engineering Structures,2001,23:407 -424.
[6] 叶燎原,潘文.结构静力弹塑性分析(push-over)的原理和计算实例[J].建筑结构学报,2000,21(1):37-43.Ye Liaoyuan,Pan Wen.The principle of nonlinear static analysis(push-over)and numerical examples[J].Journal of Building Structures,2000,21(1):37 -43.(in Chinese)
[7] 尹华伟,易伟建.结构地震反应Pushover位移形状向量的选取[J].湖南大学学报:自然科学版,2004,31(5):88-93.Yin Huawei,Yi Weijian.Displacement shape vector selected for static pushover analysis of the structural seismic responses[J].Journal of Hunan University:Natural Sciences,2004,31(5):88 -93.(in Chinese)
[8] Kapil Khandelwal,Sherif EI- Tawil,Fahim Sadek.Progressive collapse analysis of seismically designed steel braced frames[J].Journal of Constructional Steel Research,2009,65:699 -708.
[9] 北京金土木软件技术有限公司.Pushover分析在建筑工程抗震设计中的应用[M].北京:中国建筑工业出版社,2010.

