基于模糊PID方法的ROV操纵控制仿真

刘可峰，连 琏，曹俊亮，王秋智

(1.上海交通大学船舶海洋与建筑工程学院，海洋工程国家重点实验室，上海200240)(2.江苏科技大学船舶与海洋工程学院，江苏镇江212003)

随着海洋科学研究的逐步推进，人类探索的海洋深度越来越大，由于水下遥控机器人(remotely operated vehicle，ROV)强大的深海作业和长时间续航的能力，使其在海洋科学考察、资源开探、设备维护等方面得到越来越多的应用.面对复杂的海洋环境、高强度的作业需求和ROV自身动力学模型的高度非线性，ROV的控制问题成为急需研究解决的难题之一，高性能的ROV控制系统对ROV系统的研究开发具有非常重要的意义.

为了满足工程应用中航迹跟踪和运动状态保持等需求，需要ROV具备良好的操控性能和较高的运动精度，从而使许多控制方法在ROV系统中得到了应用研究.传统的PID控制方法因其使用的方便性在工程实际中仍然得到广泛应用，文献［1］在无人潜水器垂直面运动控制研究中应用PID方法.文献［2］应用PID 算法进行了潜艇低速运动时的操纵控制研究.文献［3］应用滑模观测器研究了一种水下运载器多变量鲁棒输出反馈控制方法.针对目前一些先进控制方法在ROV系统中单独应用的劣势，多种控制方法的组合应用得到较大的发展.文献［4］应用模糊滑模进行了水下机器人在浪涌中横摇角的控制研究.文献［5］在水下机器人控制研究中应用了神经网络和滑模的组合控制方法.文献［6］则在前者基础上应用了神经网络、滑模和遗传算法的组合控制方法.这些方法具有各自的优缺点，传统PID控制方法因为应用简便而得到广泛使用，但是对系统参数和环境变化的适应性差，传统的模糊控制方法需要一定的工程应用经验，而神经网络控制方法则需要一定的训练时间，系统实时性不够好.

针对ROV在深海作业中定向、定高等运动性能对高精度控制系统的需求，文中采用了一种模糊PID控制算法实现了自适应模糊PID复合控制，并针对常规PID控制算法的不足进行了相应的改进，使控制系统获得良好的动态特性和控制精度，通过仿真和实验对比验证了控制方法的正确性和优越性.

1 ROV运动模型

文中以中型海底作业机器人为研究对象，其设计目标为海洋观测，数据采集和海底作业，该ROV采用核心开框式结构，上部设置浮力材料，作业时配载成零浮力平衡状态，为满足作业需要，要求其具有定向、定高和定深等自动航行能力.为研究的统一性，文中的坐标系、名词和符号均采用国际水池会议(ITTC)推荐的坐标系统，潜器的运动模型通常采用两套右手坐标系统，一套是固定坐标系E-ξηζ，另一套是运动坐标系G-xyz(图1)，分别用于运动的水动力特性和轨迹姿态模拟.

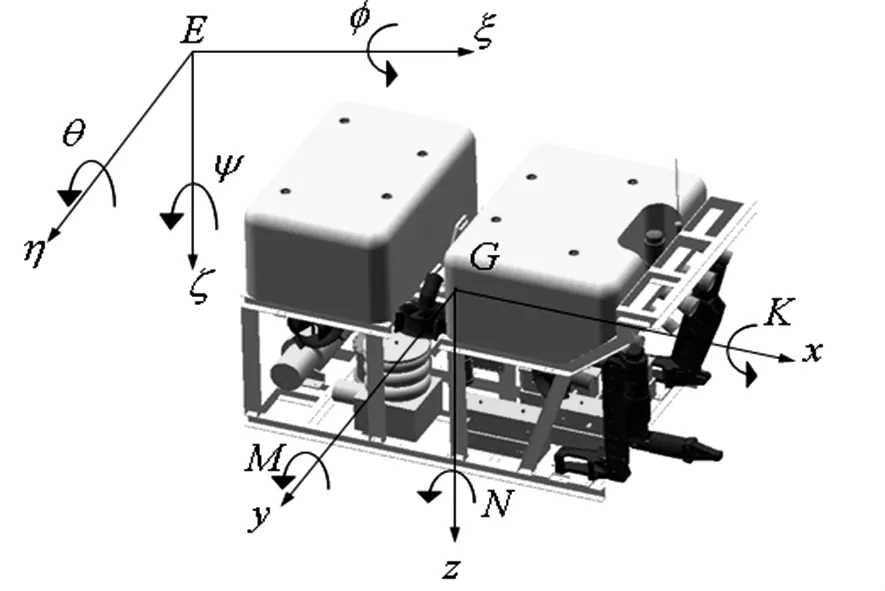
图1 中型作业机器人Fig.1 Middle manipulation ROV

ROV的操纵数学模型沿用格特勒潜艇标准运动方程，潜艇水下空间运动方程概括起来包含了3个轴向移动方程和3个绕轴向转动方程［7］，在其基础上根据所研究ROV对定向、定高和定深的机动能力需求作相应修改和简化，忽略垂直面对水平面的一些影响，并忽略模型中一些高阶项和外部环境力等影响，得到了该ROV适用的四自由度运动方程，其动力学方程为:

式中:m为潜器质量;Iz为潜器对Gz轴的转动惯量;u，v，w和r为潜器的纵向、横向、垂向线速度和艏向角速度;·u，·v，w·和·r 为潜器纵向、横向、垂向线加速度和艏向角加速度;XT，YT，ZT和NT分别为推进器在3个方向上的推进力及水平面力矩;其他均为潜器水动力系数.

为实现设计所需的操纵性能，该ROV配置了6台液压马达驱动的等厚导管螺旋桨［8］，其中2台推进器以一定角度倾斜布置在顶部两侧，4台推进器以X型互相垂直布置在水平面内(图2)，以实现高效的矢量推进性能，达到ROV设计需求的纵向、横向、垂向运动和艏向转动的能力.

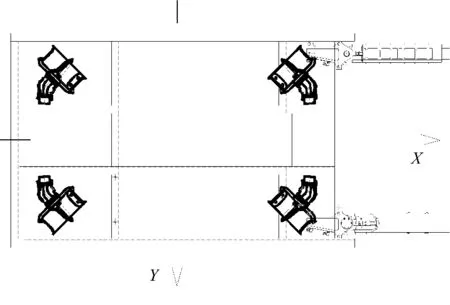
图2 ROV水平面推进器布置Fig.2 Arrangement of the ROV horizontal thrusteres

设6 个推进器的推力分别为 t1，t2，t3，t4，t5，t6，可用矩阵表示为 Tp= ［t1t2t3t4t5t6］T，与ROV所需推力的矢量矩阵FP=［XTYTZTNT］T的关系为:

式中A为与推进器装配位置相关的推力转换矩阵，可表示为:

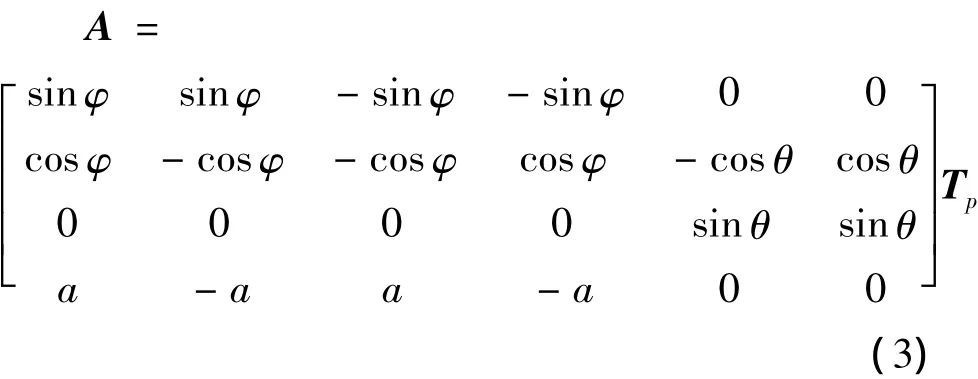
式中:φ为水平面推进器与纵向的布置夹角;θ为垂直面推进器与水平面的布置夹角;a为水平面推进器推力矢量相对ROV水平面质心的力臂.

ROV运动方程需要的是各运动矢量方向上的推力和力矩，而工程上控制的是各推进器所发出的推进力，需要转换矩阵A的伪逆矩阵A+，从矢量推力和力矩反向计算出各推进器所需发出的推力:

采用各推进器推力Tp表示的ROV运动模型的状态方程为:

式中:X=[ u v w r]T，B=M-1P，C=M-1A，

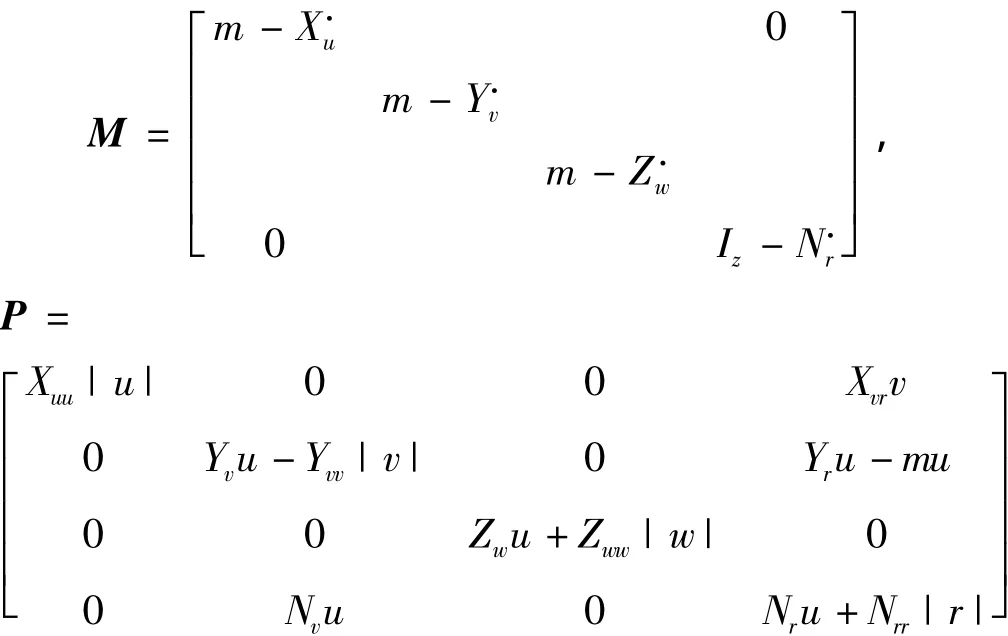
2 模糊PID控制器

传统PID控制器是一种线性控制器，其特点是使用简单，只需对控制器的比例、积分和微分3个系数进行调整，就可获得所需的结果.但是PID控制器需要精确的数学模型［9］，并且单组参数难以满足控制量在较大范围内变化时的需要.

针对此类控制需求，应用结合模糊控制原理的模糊PID控制方法［10］来解决工程实际的需要，其控制结构如图3.该系统由一个PID控制器和模糊控制器组合而成，模糊控制器以偏差e和偏差变化率ec为输入，利用模糊控制规程在线对PID参数进行修改，可以根据不同时刻系统对PID参数的要求，实时调整输出PID控制器的3个参数KP，KI，KD.

输入语言变量取为偏差e和偏差变化率ec的绝对值，每个语言变量取大(B)，中(M)和小(S)3个语言值.图4为定向航行控制时偏差和偏差变化率的隶属函数，其中e为艏向角偏差，ec为艏向角变化率.图5为定高控制时偏差和偏差变化率的隶属函数，其中e为高度偏差，ec为高度变化率.

图3 模糊PID控制结构Fig.3 Control structure of fuzzy PID

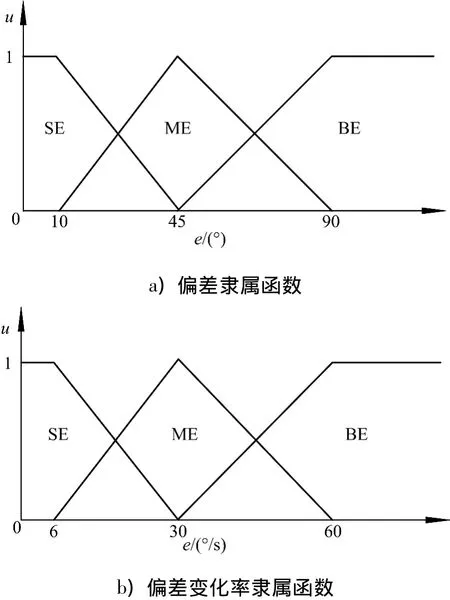
图4 定向航行时偏差的隶属函数Fig.4 Deviation subordinate function of orientation keeping

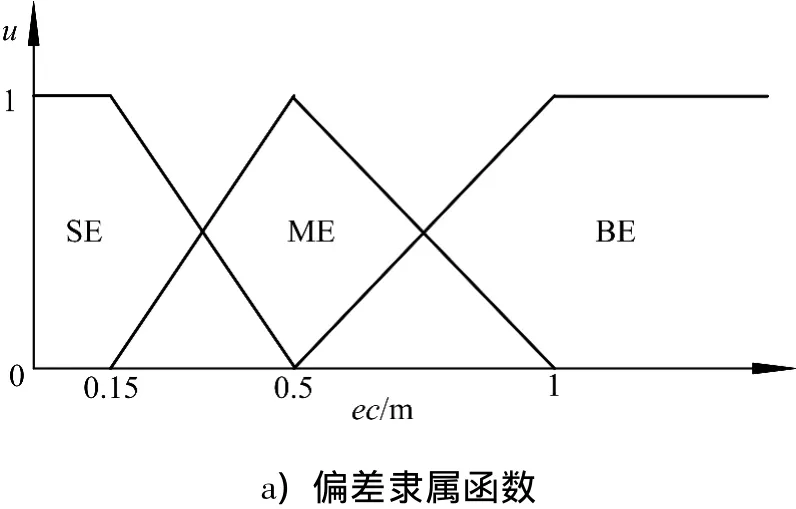
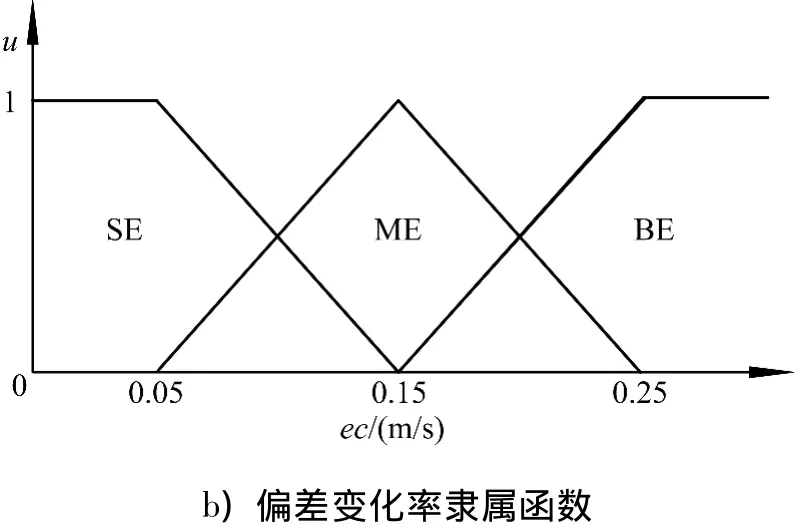
图5 定高控制时偏差的隶属函数Fig.5 Deviation subordinate function of height keeping

设偏差e和偏差变化率ec的绝对值有5种状态组合:

1)|e|=B

2)|e|=M＆|ec|=B

3)|e|=M＆|ec|=M

4)|e|=M＆|ec|=S

5)|e|=S

每种状态的隶属度可分别对应如下关系式:

1)μ1(|e|，|ec|)=μBE(|e|)

根据2.1小节机组的造价分析，在建设天然气发电方面，平均造价约为0.068亿元/MW。因此，岛内建设天然气电厂投资F(亿元)与建设容量S(MW)的近似关系为：

2)μ2(|e|，|ec|)= μBE(|e|)Λ μBC(|ec|)

3)μ3(|e|，|ec|)= μME(|e|)Λ μMC(|ec|)

4)μ4(|e|，|ec|)= μME(|e|)Λ μSC(|ec|)

5)μ5(|e|，|ec|)=μSE(|e|)

根据实时偏差e和偏差变化率ec测量值的绝对值，可用下面的解模糊式来计算PID的3个参数:

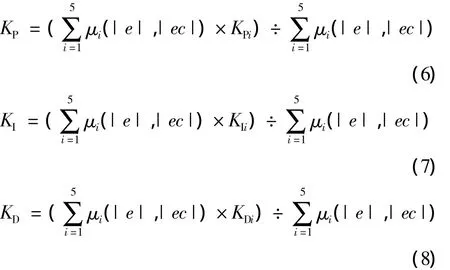
式中KPi，KIi，KDi是PID的3个参数在不同状态下的加权，它们在不同状态下可取为:

1)KP1=K′P1，KI1=0，KD1=0

2)KP2=K′P2，KI2=0，KD2=K′D2

4)KP4=K′P4，KI4=0，KD4=K′D4

5)KP5=K′P5，KI5=K′I5，KD5=K′D5

其中 K′P1～ K′P5，K′I1～ K′I5，K′D1～ K′D5为不

同状态下用常规PID参数整定法取得的整定参数值.

3 仿真结果及分析

文中以研制中的中型海底作业机器人为研究对象，其主尺度为2.473 m×1.3 m×1.5 m(长×宽×高)，水平面推进器和纵向的布置夹角φ为45°，垂直面推进器与水平面的布置夹角θ为80°，水平面推进器推力矢量对质心的布置力臂a为0.798 m.为了保证所建立模型的精度，应用设计软件SolidWorks三维几何建模计算得其质量为1 860 kg，对Z轴的转动惯量为3587kg·m2，并进行了一系列水动力实验来取得水动力系数，经过数值处理和无因次换算后得到的部分水动力系数如表1.

表1 ROV水动力系数Table 1 Hydrodynamic coefficients of the ROV

根据以上公式原理和水动力系数，利用Matlab/Simulink软件进行模拟仿真，应用传统PID和模糊PID两种控制方法来进行该中型ROV的操控研究，从而对比分析两种方法的特点.为获得良好的系统控制性能，对控制参数的选择要反复权衡.当|e|较大时，取较大KP可使系统在初始阶段有较大的响应速度;当|e|和|ec|中等大小时，为使系统响应的超调减少，KP应取较小值，KD的大小应适中且变化要平滑以保证系统的响应速度;当|e|较小时，应增大KP和KI值从而保证系统具有良好的稳态性能，KD值取的要合适以减少系统在设定值附近的震动.

在上海交通大学海洋水下工程科学研究院实验水池进行了一系列潜器样机实验，仿真模拟研究选择实验中某定速定向航行工况进行，ROV以1节速度向前航行时，控制艏向角从0°变化到60°，模拟仿真和水池实验过程的数据对比情况如图6，模糊PID控制方法相对传统PID方法具有更好的系统动态性能，显示了模糊控制方法的优越性.由仿真数据与实验曲线的对比可见，模拟仿真与水池实验的吻合度较好，显示了所用模拟仿真方法的可靠性.

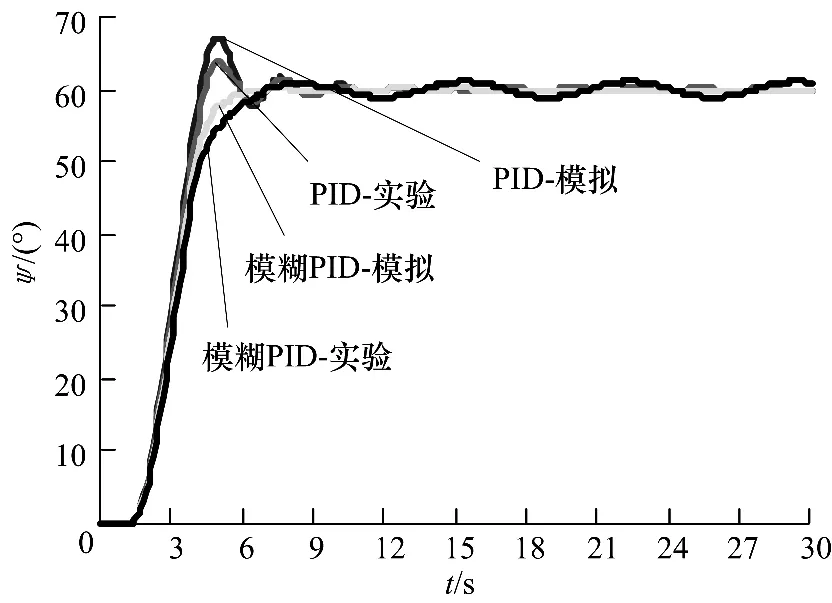
图6 两种方法的模拟和实验中艏向角变化曲线Fig.6 Heading angle curves of two methods

传统PID由于系统固有的特点，比较适应某一固定工作点附近的系统控制，而模糊PID方法的适应范围较广.艏向角0～30°变化仿真时，ROV艏向角和艏向角速度的响应曲线如图7.对比艏向角在0～60°变化过程，传统PID方法在工况变化较大时适应性较差，而模糊PID方法则在两个工作点都取得了较好的控制性能，超调量较小，系统震荡较小.

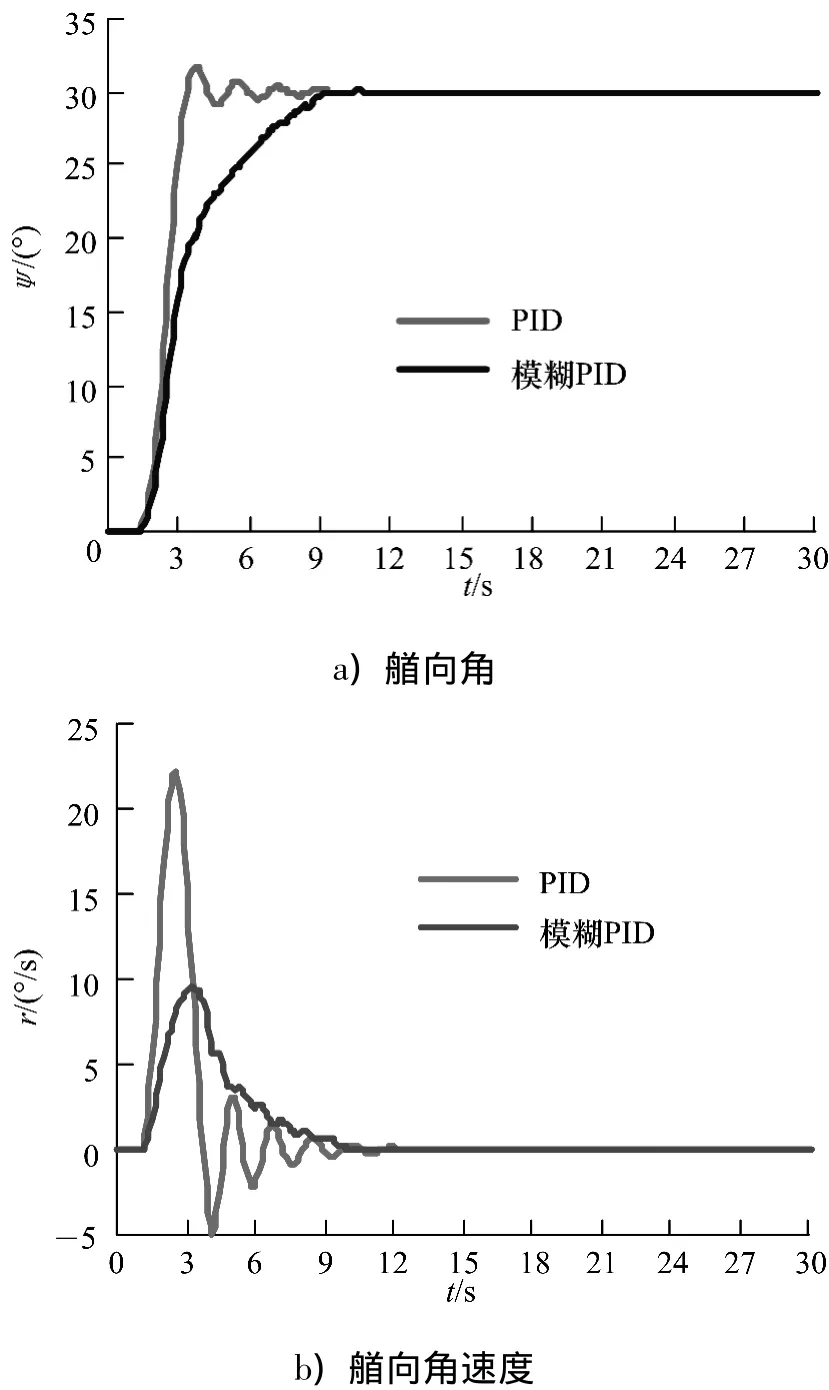
图7 小角度变化时艏向角和艏向角速度仿真曲线Fig.7 Heading angle and heading angle velocity simulation curves of small angle changing

深度控制的模拟和实验数据符合程度也较好，如图8，从高度为4.4 m(水池水面高度)至2.2 m的实验曲线，模糊PID控制方法同样显示了较好的系统响应特性.

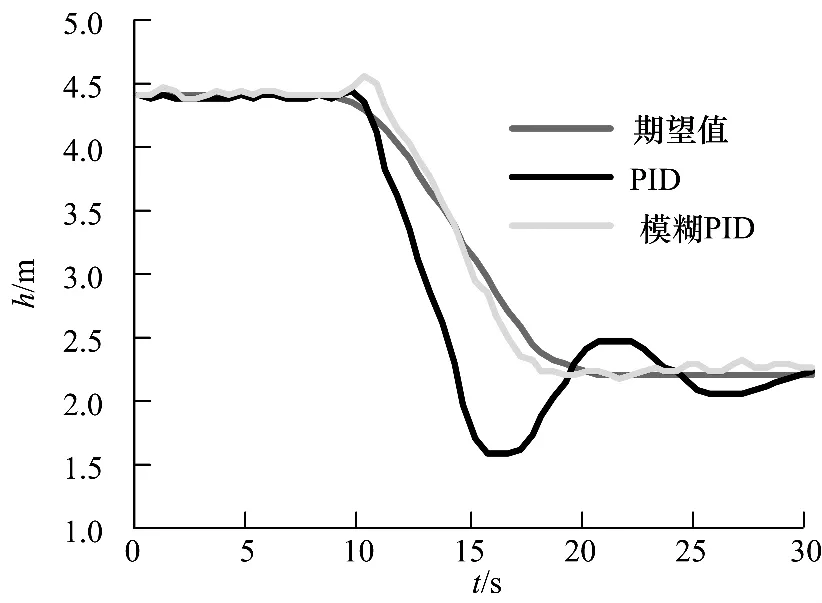
图8 深度变化实验曲线Fig.8 Height curves of experiment

4 结论

根据文中运动仿真和水池实验数据的对比分析表明，模糊PID控制方法应用于作业型ROV的操纵控制中，对各种复杂工况具有较好的适应能力，并且可以沿用传统PID方法中一些对参数设定的方法.

模糊PID方法集传统PID和模糊控制两种方法的优点，通过仿真和水池试验验证其优点，但水池实验环境比较简单，还需进一步经过海试进行完善，提高控制方法应付实际复杂海况的能力，进一步改进提升该方法的操纵控制性能.

References)

［1］ 张勋，边信黔，唐照东，等.AUV均衡系统设计及垂直面运动控制研究［J］.中国造船，2012，53(1):28-36.Zhang Xun，Biang Xinqian，Tang Zhaodong，et al.Design of balance system for AUV and study on motion control in vertical plane［J］.Shipbuilding of China，2012，53(1):28 -36.(in Chinese)

［2］ 刘可峰，连琏，姚宝恒.潜艇低速运动时操纵控制仿真［J］.舰船科学技术，2014，36(11):18-22.Liu Kefeng，Lian Lian，Yao Baoheng.Simulation on manoeuvre and control of submarine under low speed［J］.Ship Science and Technology，2014，36(11):18 -22.(in Chinese)

［3］ 朱康武，顾临怡，马新军，等.水下运载器多变量鲁棒输出反馈控制方法［J］.浙江大学学报，2012，46(8):1397-1406.Zhu Kangwu，Gu Linyi，Ma Xinjun，et al.Studies on multivariable robust output feedback control for underwater vehicles［J］.Journal of Zhejiang University，2012，46(8):1397 -1406.(in Chinese)

［4］ 刘和平，龚振邦，李敏，等.水下机器人浪涌中横摇角的模糊滑模控制［J］.武汉理工大学学报，2009，31(14):122 -133.Liu Heping，Gong Zhenbang，Li Min，et al.Fuzzy sliding mode control on the rolling of underwater robot in wave［J］.Journal of Wuhan University of Technology，2009，31(14):122 -133.(in Chinese)

［5］ Bagheri A，Moghaddam J J.Simulation and tracking control based on neural-network strategy and slidingmode control for underwater remotely operated vehicle［J］.Neurocomputing，2009，72(3):1934 -1950.

［6］ Javadi-Moghaddam J，Bagheri A.An adaptive neurofuzzy sliding mode based genetic algorithm control system for underwater remotely operated vehicle［J］.Expert Syst，2010，37(3):647 -660.

［7］ 施生达.潜艇操纵性［M］.北京:国防工业出版社，1995.

［8］ 刘可峰，姚宝恒，连琏.深潜器等厚导管螺旋桨敞水性能计算分析［J］.船舶工程，2014，36(1):37-40.Liu Kefeng，Yao Baoheng，Lian Lian.Calculation and analysis of open water performance for submersibles identical thickness ducted propellers［J］.Ship Engineering，2014，36(1):37-40.(in Chinese)

［9］ 朱志强，江紫亚，何玉庆，等.PID控制器的频域特性与无模型参数调节［J］.控制与决策，2014，29(10):1833-1838.Zhu Zhiqiang，Jiang Ziya，He Yuqing，et al.Frequency properties of PID controller and medel free tuning［J］.Control and Decision，2014，29(10):1833 -1838.(in Chinese)

［10］ 王述彦，师宇，冯忠绪.基于模糊PID控制器的控制方法研究［J］.机械科学与技术，2011，30(1):166 -172.Wang Shuyan，Shi Yu，Feng Zhongxu.A method for controlling a loading system based on a fuzzy PID controller［J］.Mechanical Science and Technology for Aerospace Engineering，2011，30(1):166 - 172.(in Chinese)