基于拟牛顿迭代的分数阶Fourier变换最佳阶次的搜索方法研究
陈 蓉,马菊红
(1.苏州大学 城市轨道交通学院,江苏苏州215006)(2.江苏科技大学图书馆,江苏镇江212003)
作为经典傅里叶变换的广义形式,分数阶傅里叶变换(fractional Fourier transform,FRFT)可理解为Chirp基分解,特别适合处理Chirp类信号,对其具有良好的检测和识别效果,广泛应用于雷达信号处理等领域[1-4].在分数阶傅里叶变换的应用研究中,如何确定FRFT的最佳变换阶次成为热点问题[5].现有成果中,对于最佳阶次的确定问题,多采用变换域参数的二维搜索方法,算法的估计精度和运算量之间存在严重的矛盾.为解决这一问题,文献[6]提出了先以大步进值进行二维粗搜索,再利用拟牛顿迭代局部细搜索的方法;文献[7]指出拟牛顿迭代方法在这一应用中具有较好的效果.然而,目前尚无对拟牛顿迭代具体实现方法的讨论,使之在实际应用中缺乏指导.
针对上述问题,文中研究了拟牛顿迭代算法的基本原理及实现方法,通过仿真实验展现了该方法搜索FRFT最佳变换阶次的收敛过程,并分析讨论了其在实际应用中存在的利弊.
1 基于FRFT的Chirp信号二维搜索检测法
时域信号x(t)的分数阶Fourier变换定义为:
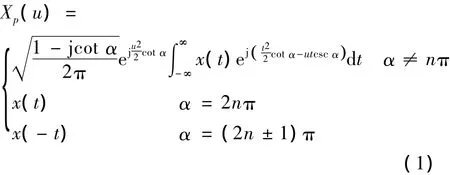
式中:p为FRFT变换的阶数;α为FRFT轴与时间轴之间的夹角,且;n为整数.
设Chirp信号的时域表达式为:

式中:A为Chirp信号的幅值;φ0为初始相位;f0为起始频率;k0为信号的调频率;B为信号的带宽;T为脉冲宽度.为简化计算,一般设φ0=0.则根据式(1),Chirp信号的分数阶Fourier变换为:

当k0+cot α =0时,记α为α0,称为最佳FRFT旋转角度,且有

式中Sa(·)为辛格函数.
由式(4)可以看出,时限Chirp信号经最佳阶次的分数阶Fourier变换后,能量区域的主瓣宽度为.当f- ucsc α =0时,|X(u)
0α0|2达到峰值.利用该性质,基于FRFT的Chirp信号二维搜索检测法的基本思路可简述为:以旋转角度α(或变换阶次p)为变量进行扫描,对观测信号连续做分数阶Fourier变换,从而形成信号能量在参数(α,u)(或(p,u))平面上的二维分布.在此平面上按阈值进行峰值点的二维搜索即可实现Chirp信号的检测与参数估计,该过程可描述为:
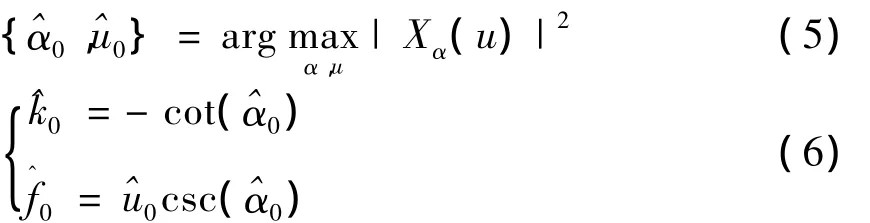
2 拟牛顿迭代法的基本原理及实现
2.1 拟牛顿迭代法的基本原理
针对实数域和复数域上近似求解方程的问题,牛顿提出了一种高效的方法——牛顿迭代法.由于利用了目标函数的二阶导数信息,故算法收敛速度快.然而,由于牛顿迭代法要求计算包含二阶导数信息的Hessian矩阵及其逆矩阵,其计算复杂度高、内存占用大.此外,若目标函数的二阶导数不存在,或逆矩阵不存在,则该法无法使用.
拟牛顿迭代算法对上述问题进行改进,其利用直接构造的与Hessian矩阵的逆矩阵相近的正定矩阵代替目标函数的二阶偏导数计算.经典牛顿法的迭代公式为:

式中:xk,xk+1分别为第k次和第k+1次迭代求得的极值;λk为步长因子,在牛顿迭代法中取值固定为1;sk= -[H(xk)]-12f(xk),称为牛顿方向,其中f(x)为目标函数,[H(xk)]-1=22f(xk)-1为Hessian矩阵的逆矩阵.
要构造22f(xk)-1的近似矩阵Hk,就要先分析22f(xk)-1和一阶导数之间的关系.令在第k次迭代后,得到点xk+1,将目标函数f(x)在点xk+1展开成泰勒级数,并取二阶近似,得到:

则在xk+1附近有:

令x=xk得:

则有 qk≈ 22f(xk+1)mk.
设Hessian矩阵22f(xk+1)可逆,则

当计算得到mk和qk后,依据式(11),估计在xk+1处的Hessian矩阵的逆.为了用不包括二阶导数的矩阵Hk+1取代经典牛顿法中的Hessian矩阵的逆矩阵,就需要令Hk+1满足

式(12)即为拟牛顿条件.
在拟牛顿迭代算法中将Hk作为Hk+1的近似来构造,考虑到22f(xk)为对称矩阵,因此要求Hk满足条件:①对称;②满足拟牛顿条件方程.
设Hk-1经过简单修正可得到Hk,即

式中:对称矩阵Ek称为校正矩阵.显然,满足式(13)的对称矩阵不止一种,Hessian矩阵的构造方法不同将产生不同的拟牛顿法,因此拟牛顿迭代法是一族算法.
2.2 拟牛顿迭代法的迭代步骤
在众多Hessian矩阵的构造方法中,BFGS算法[8]是效率较高的一种,尤其是针对无约束最优化问题算法中采用的校正公式为
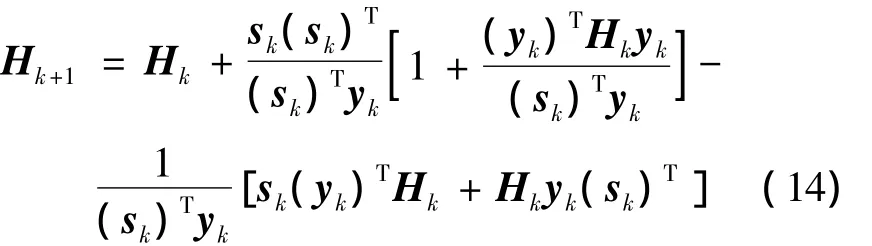
式中:sk=xk+1- xk,yk=2f(xk+1)- 2f(xk).为确保目标函数的下降,矩阵Hk必须满足正定性,而Hk保持正定的充分必要条件是skTyk>0,这是在构造近似矩阵中需要保证的.此外,在迭代一定次数后,BFGS算法还将重置初始点和迭代矩阵[9].
以BFGS算法为例,拟牛顿迭代法的迭代步骤如下:
1)给定初始点x0,初始矩阵H0=In及搜索精度ε>0;
2)若‖2f(x0)‖≤ε,停止,极小点为x0;否则转步骤3);
3)取m0=-H02f(x0),且令k=0;
4)用一维搜索法求tk,使得tkf(xk+tkmk)=,令 xk+1=xk+tkmk;
5)若‖2f(xk+1)‖≤ε,停止,极小值点为xk+1;否则转步骤6);
6)若k+1=n,令x0=xn,转步骤3);否则转步骤7);
7)令

其中:sk=xk+1- xk,yk=2f(xk+1)- 2f(xk),取mk= - Hk+12f(xk+1),置 k=k+1,转步骤4).
2.3 仿真实验
拟牛顿迭代法是下降类迭代方法,故基于拟牛顿迭代的分数阶Fourier变换最佳变换阶次的极值搜索问题可描述为:在参数(p,u)平面上,寻找合适的(p0,u0),使得目标函数 f(p,u)= -|Xp(u)|2达到最小.与公式(5)对应,该过程可描述为:

为了兼顾精度和高效计算的要求,文中首先采用大步进值做二维峰值搜索,获取p的粗估计结果,然后再利用拟牛顿法逼近极值点.实验中,采用线性调频雷达,其主要参数为脉冲宽度T=10μs,中心频率 f0=545MHz,带宽B=k0T=30MHz,发射波长λ=0.025m,采样频率为fs=5B.热噪声采用高斯白噪声模拟,信噪比为 -2 dB.搜索步进值为0.01,经二维峰值搜索得,量纲归一化[10]后p的粗估计结果为^p=1.13.设拟牛顿迭代法初始值p=1.13,在该值附近采用拟牛顿迭代法搜索到最佳值的过程,如图1.

图1 拟牛顿迭代法的搜索过程Fig.1 Searching process of Quasi-Newton method
拟牛顿法搜索到最佳变换阶次p=1.1255,以该阶次做FRFT,其仿真结果如图2.Chirp信号在估计所得的最佳分数阶傅里叶域中实现了很好的能量聚集性.
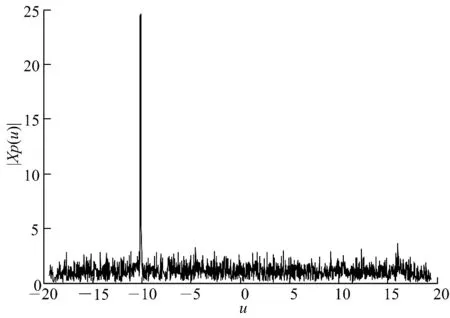
图2 信噪比-2dB时,Chirp信号在估计所得最佳变换阶次下的分布Fig.2 Distribution of Chirp signal in the estimated optimal fractional Fourier transform domain when the SNR is-2dB
图3是将信号x(t)通过-10 dB的加性高斯白噪声信道后,利用拟牛顿迭代法搜索到的最佳FRFT阶次对信号进行FRFT处理的结果.

图3 信噪比-10dB时,Chirp信号在估计所得最佳变换阶次下的分布Fig.3 Distribution of Chirp signal in the estimated optimal fractional Fourier transform domain when the SNR is-10dB
显然,Chirp信号在该FRFT变换阶次下未能实现良好的能量聚集,即拟牛顿迭代法的输出结果与信号实际的最佳FRFT变换阶次间存在较大误差.导致这一结果的原因在于,当噪声强度较大时,信号在分数阶二维平面的能量聚集将出现较强的虚假极值点,若迭代搜索初始值或步长选择不当,即会致使拟牛顿迭代法无法收敛到全局最优点.
另一方面,为验证拟牛顿法的运算速度,在MATLAB程序中添加tic和toc函数,获取搜索出最佳极值点的耗时量,将该时间与直接进行二维搜索的耗时量相比较,结果如表1.实验中,二维搜索法中粗搜索的步进值为0.01,细搜索的步进值为0.0001;二维粗搜索加拟牛顿精搜中二维粗搜索的步进值为0.01.[1] 唐江,赵拥军,朱健东,等.基于FRFT的伪码-线性
调频信号参数估计算法[J].信号处理,2012,28(9):
1271-1277.
Tang Jiang,Zhao Yongjun,Zhu Jiandong,et al.FrFT-
based parameter estimation for PRBC-LFM signals[J].
Signal Processing,2012,28(9):1271-1277.(in Chi
nese)

表1 变换阶次估计算法的执行速度比较Table 1 Comparison of execution speed of different algorithms
表1中,理论值和估计值之间会有微小的误差,这是由信号的离散化采样造成的.由表1可知,拟牛顿迭代法在分数阶FRFT最佳变换阶次的快速搜索方面上具有较大优势.
3 结论
文中对基于拟牛顿迭代的FRFT最佳变换阶次的搜索方法进行了深入研究,给出了其在Chirp信号检测这一实际应用中的具体实现步骤,并通过仿真实验展现了拟牛顿迭代法搜索分数阶Fourier变换最佳变换阶次的收敛过程.由于拟牛顿迭代算法是一种局部搜索法,其仅能收敛到初始值周围的极值点,因此,初始值的选取至关重要,文中采用了二维粗搜索方法获取初值.实验表明,当二维粗搜索所得结果合适时,利用拟牛顿搜索方法不仅可以保证搜索精度,更能提高搜索效率.但是,当信噪比较低时,二维粗搜索所得初值准确性低,直接影响后续迭代搜索结果.因此,抗噪性强的初值选取方法需在后续进一步研究.
References)
[2] 邓兵,王旭,陶然,等.基于分数阶傅里叶变换的线性调频脉冲时延估计特性分析[J].兵工学报,2012,33(6):765-768.Deng Bing,Wang Xu,Tao Ran,et al.Performance analysis of time delay estimation for linear frequencymodulated pulse based on fractional fourier transform[J].Acta Armamentarii,2012,33(6):765 - 768.(in Chinese)
[3] 张军,周旭.LFMCW雷达多目标检测技术研究[J].现代雷达,2013,35(6):29 -33.Zhang Jun,Zhou Xu.A study on multi-object detection for LFMEW radar[J].Modern Radar,2013,35(6):29-33.(in Chinese)
[4] 向崇文,刘锋,黄宇,等.基于FRFT循环处理的LFM-PRBC雷达信号截获与特征提取[J].弹箭与制导学报,2013,33(2):117 -124.Xiang Chongwen,Liu Feng,Huang Yu,et al.Interception and feature extraction of LFM-PRBC Radar signal based on FRFT cyclic processing method[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(2):117 -124.(in Chinese)
[5] 陈小龙,关键,黄勇,等.分数阶Fourier变换在动目标检测和识别中的应用:回顾和展望[J].信号处理,2013,29(1):85 -97.Chen Xiaolong,Guan Jian,Huang Yong,et al.Application of fractional fourier transform in moving target detection and recognition:development and prospect[J].Signal Processing,2013,29(1):85 -97.(in Chinese)
[6] 齐林,陶然,周思永,等.基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J].中国科学E 辑,2003,33(8):749 -759.Qi Lin,Tao Ran,Zhou Siyong,et al.Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J].Science in China E,2003,33(8):749 -759.(in Chinese)
[7] 卫红凯,王平波,蔡志明,等.分数阶Fourier变换极值搜索算法研究[J].电子学报,2010,38(12):2949-2952.Wei Hongkai,Wang Pingbo,Cai Zhiming,et al.Study of algorithm for extremum seeking in the fractional fourier transform[J].Acta Electronica Sinica,2010,38(12):2949 -2952.(in Chinese)
[8] 耿红梅.BFGS算法综述[J].大众科技,2011(11):3-4,10.Geng Hongmei.A summary of BFGS algorithm[J].Popular Science& Technology,2011(11):3 - 4,10.(in Chinese)
[9] 陈宝林.最优化原理与算法[M].北京:清华大学出版社,2005:39-47.
[10] 陶然,邓兵,王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社,2009:144-147.

