广义严格对角占优矩阵的一个判定方法

崔丽娜

（齐齐哈尔工程 学院基础部，黑龙江 齐齐哈尔 161005）

广义严格对角占优矩阵的一个判定方法

崔丽娜

（齐齐哈尔工程 学院基础部，黑龙江 齐齐哈尔 161005）

文章根据所给的引理给出了一个判定广义严格对角占优矩阵的方法。

对角占优矩阵；充分条件；特征值包含域

我们先给出一个引理。

引理 设A=(aij)∈Cn×n，aij＞0,(0≤i≤n)，若B=A+AT是非奇异M-矩阵，则A为广义严格对角占优矩阵。

证明：由于B是非奇异M-矩阵，并且是实对称矩阵，这时B的特征值全部为正值，根据商值定理，对任何实向量（复向量）Z≠0，我们认为

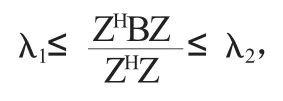
这里λ1和λ2分别是的最小特征值和最大特征值，ZH是Z的共轭转置。设A的任一特征值μ所对应特征向量为Y，则AY=μY,利用商Rayleigh值定理有

因为YHBY=YH(A+AT)Y=YHAY+YHATY=μYHY+μYHY= (2Reμ)(YHY)，因此由上述不等式可得

又由于B是M-矩阵，可有λ1＞0，故有2Reμ＞0，即Re μ＞0，即中任意特征值的实部全部是正值。由引理6知，A为非奇异M-矩阵，即μ(A)=A也为非奇异M-矩阵。因此，A为广义严格对角占优矩阵。

通过引理来证明下面定理。

定理 设A=(aij)n×n，若α∈[0,1]，使

2 aij+(2α-1)Ri＞0，

则A∈H。

证明 当定理1给定的条件成立时，取

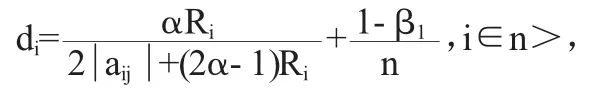
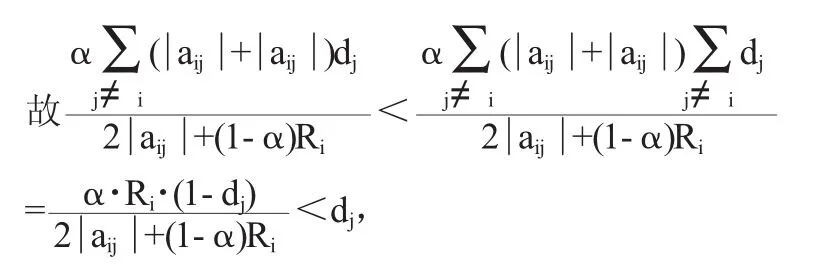
i∈n＞，则有

其中设B=μ(A)+μ(A))T=(bij)n×n，由上式可以有

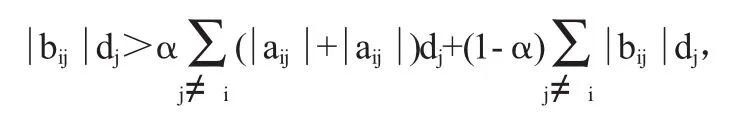
则知B是广义严格α对角占优矩阵。由定理可知B是M-矩阵，再根据引理可知A为广义严格对角占优矩阵，即A∈H。

[1]高益明.矩阵广义对角占优和非奇判定[J].东北师大学报：自然科学版，1982，（3）：23-28

[2]孙玉祥.广义对角占优矩阵的充分条件[J].高等学校计算数学学报，1997，（3）：216-223

[3]Sun Yuxiang.An Improvement on a Theoerem by Ostrouski and Its Application[J].Northeastern Math.J,1997，（7）497-502.

[4]黎稳.广义对角占优矩阵的判别准则[J].应用数学与计算数学学报, 1995,9(2)：35-38.

A Determination Method of Generalized Strictly Diagonally Dominant Matrix

CUI Li-na (Department of Basic Courses,Qiqihar Engineering College,Qiqihar,Heilongjiang 161005,China).

The article proposed a method for generalized strictly diagonally dominant matrix according to the given lemmas.

diagonally dominant matrix;a sufficient condition;characteristic value inclusion region

O151.21

A

2095-980X（2015）02-0137-01

2015-01-18

崔丽娜（1981-），女，辽宁辽阳人，硕士研究生，讲师，主要研究方向：基础数学。