基于最优二次型理论的滚转导弹三回路驾驶仪设计与研究

范世鹏，林德福，姚怀瑾，路宇龙，祁载康

(1.北京理工大学 宇航学院，北京100081;2.北京航天自动控制研究所，北京100854;3.北京电子工程总体研究所，北京100854)

0 引言

由美国Raytheon 公司首次提出的经典三回路驾驶仪以其良好的性能和工程可实现性而被广泛采用。三回路驾驶仪以一阶实根为主导极点，而通过选取二阶共轭复根可改变开环穿越频率，保证系统拥有足够的幅相裕度［1-6］。这种驾驶仪存在多种结构，通过不同方法重构攻角，形成伪攻角反馈，都能使系统鲁棒性得以改善［4］。

最优二次型(LQR)理论在工程中已经得到了广泛应用。Mracek 等［7］、Wise［8］利用最优/经典理论设计、分析了单通道自动驾驶仪;Nesline 等分析了LQR 设计常常出现系统失稳的原因，并指出必须对开环穿越频率进行约束［9］;Williams 等运用LQR方法为倾斜转弯(BTT)导弹多输入多输出(MIMO)系统设计控制系统［10］;文献［11 -12］采用LQR 方法，通过对比研究最优制导律独立设计和制导/控制一体化设计，指出了一体化设计的优越性;而Li 等在采用古典控制理论为滚转导弹设计控制系统时忽略了耦合效应［13-14］。

本文建立滚转导弹存在通道耦合的动力学模型，为消除耦合的影响，基于现代控制LQR 最优理论，推导得到一种I 型系统的三回路驾驶仪结构，对比研究了MIMO 和单输入多输出(SIMO)两种设计结果;并通过分析权系数与驾驶仪性能之间的关系，旨在辅助设计者合理选取权系数。

1 滚转导弹数学模型

滚转导弹因边界层非对称畸变等原因而普遍存在马格努斯效应，这对弹体姿态运动影响较大，使俯仰、偏航存在通道耦合。另外，弹体自身滚转也将产生陀螺耦合效应。这两种效应与弹体转速相关，转速越高，则耦合效应越明显。

滚转导弹动力学建立在准弹体系下的表达形式相对简单，在线性化小扰动假设下，考虑耦合效应的轴对称滚转导弹动力学方程可表示为

式中:ϑ 为俯仰角;α 为攻角;β 为侧滑角;ψ 为偏航角;δ 为舵偏角;v 为导弹速度;ay、az为y 轴方向和z 轴方向的弹体过载;分别为俯倾力矩对攻角、舵偏角、俯倾角速率的偏导数，Jz为转动惯量;bα=T 为推力，Yα、Yδz分别为升力对攻角、舵偏角的偏导数，m 为导弹质量;为俯仰力矩对侧滑角的偏导数，ωx为导弹自旋角速率。

不难看出，俯仰、偏航动力学具有反对称通道耦合的特点，其模型如图1所示。

图1 滚转导弹俯仰/偏航动力学模型Fig.1 Pitch and yaw dynamics model of rolling missile

在此引入过载误差ey=ay-ayc，以俯仰为例，制导指令相对于控制系统而言，可视为慢变量。设为0，则过载误差可表示为

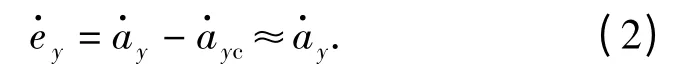
根据(1)式中过载与攻角之间的关系，将过载引入(1)式的微分方程中而消去攻角，从而得到

对偏航动力学方程作与俯仰通道相同的假设和数学等价变形。对于以上存在通道耦合的动力学模型，可将耦合效应视为外界干扰，增加一个积分环节使之形成Ⅰ型控制系统，以消除通道耦合引起的稳态误差。对以上方程组中的过载、姿态角速率相关的微分方程左右两边进行微分。

由于LQR 控制方法对数学模型准确性的要求较为严格，模型不准确对于控制系统的各项性能将有较大的影响，甚至造成系统失稳［15］。在工程实践中应用最优控制理论，应尽可能准确地建立系统的数学模型。数学模型越准确，则控制系统性能越优良［9］，因此，数学模型考虑二阶舵机环节的动态特性:

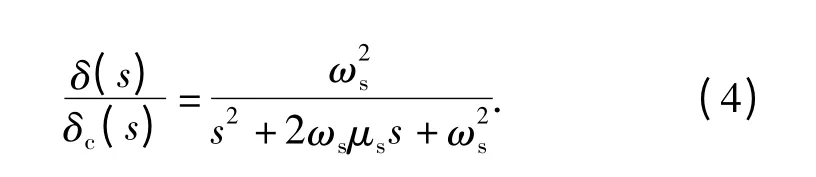
2 线性二次型最优控制

线性二次型是最优控制理论中一类典型的优化问题，其指性能泛函选取为状态变量和控制变量的二次型函数的积分形式。在合理的假设条件下，该问题所求得的控制律可以是解析的且线性的［15］。

设线性系统动态方程的状态空间表示为

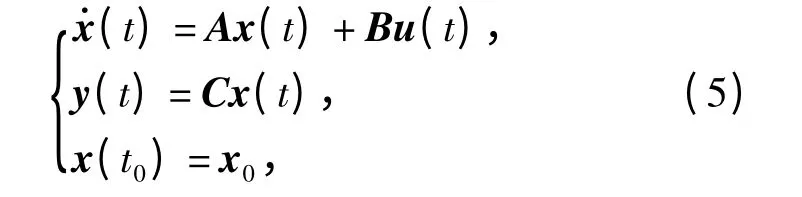
式中:x 为n 维状态变量;u 为r 维控制向量;A、B、C分别为n×n 维矩阵、n×r 维矩阵、m×n 维矩阵。

给定无限时间假设下的关于状态x(t)和控制u(t)的二次型性能指标函数:

式中:Q、R 为权系数矩阵，Q =QT≥0，为n ×n 维半正定对称阵;R=RT＞0，为r×r 维正定对称阵。

所谓二次型最优控制问题，就是寻求一个容许控制u*(t)∈Rr×r，使沿着由初态x0出发的相应状态轨迹x(t)，使性能指标函数取为极小值，即

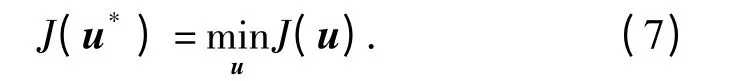
由二次型最优控制极小值理论可知，为使指标函数达到最小，最优控制律应为

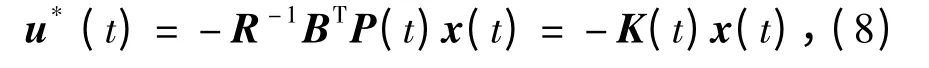
式中:P 为黎卡蒂微分方程式的解，容易证明，P 为对称正定矩阵。

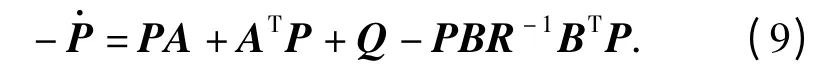
不难看出，最优控制律为线性时变的全状态反馈，且非线性的黎卡蒂微分方程求解繁琐，至少需要求解n(n +1)/2 个一阶微分方程。随着时间趋向于无穷，P(t)将趋于常值阵，最优反馈时变系统也将转换为定常系统。此时，可以用黎卡蒂代数方程式的解代替微分方程式的解。

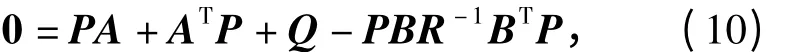
则系统的最优状态轨线x*(t)为

性能指标的最小值为

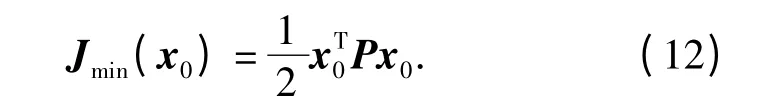
通过全状态反馈，系统的闭环极点发生变化，使系统运动遵循最优轨线，从而改善了系统的动态特性。设Lyapunov 正定函数

对L(x)求导，并将(11)式代入(13)式可得

3 三回路控制系统设计

为简化控制系统的设计，首先将状态耦合视为干扰，忽略通道耦合效应，建立俯仰通道数学模型，状态变量、控制变量和输出变量分别为

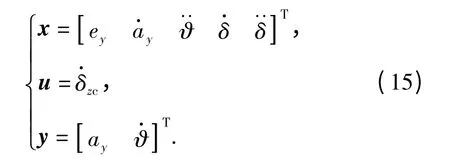
则SIMO 俯仰通道数学模型可描述为

对于具有通道耦合的滚转导弹而言，控制系统期望俯仰偏航两个通道的过载响应误差限制在一定的范围内，这不仅可使制导指令得以准确快速地执行，也可削弱通道耦合的影响;为防止弹体剧烈振荡，姿态角加速度必须加以限制;同时，控制能耗即舵偏角角速率不得过大，应对舵偏角速率进行限制。因此，提出以下指标函数:

式中:常数Ci(i =1，2，3)为权系数，其数值越大，则对相应变量的限制作用越强。对应于LQR 方法中的权系数矩阵为

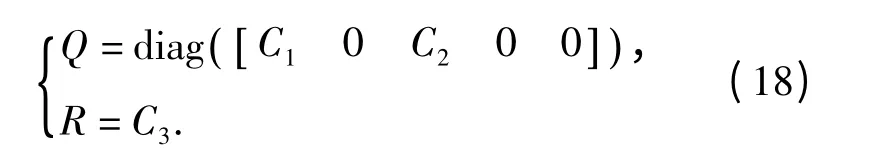
控制系统性能指标与权系数矩阵密切相关，选取不同的Ci，则得到不同的控制系统性能品质，因此，合理选取权系数是LQR 设计方法的关键。从Ci的物理意义来看，控制系统动态品质主要取决于C1，而阻尼特性、幅相裕度等与C2也有一定关系。

利用第2 节提出的LQR 方法设计控制系统，即可得到状态反馈增益矩阵K:

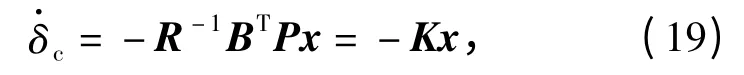
对(19)式两边进行积分，可得控制律

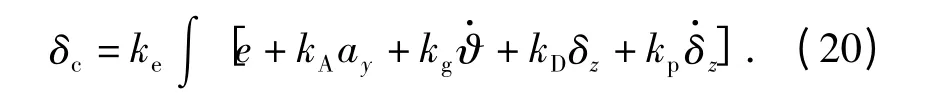
以上控制律的实现，一方面要改变舵机特性，电动舵机通过驱动电流和码盘对舵偏角速率和舵偏角进行反馈控制;另一方面，利用弹体过载和姿态角速率信息，构建了三回路驾驶仪结构，以改善弹体动态特性。图2给出了控制系统的基本结构。

图2 SIMO 设计的控制系统示意图Fig.2 Control system designed via SIMO method

闭环系统极点表征了控制器的性能优劣，研究闭环极点随着加权矩阵变化的规律可以帮助设计者选择权系数矩阵，并更好地理解特定的权系数矩阵所得到的控制器。注意到最优控制律完全取决于状态加权矩阵与控制加权矩阵的相对大小关系，这里固定C3=10 000，通过调节C1、C2，得到不同性能指标的控制器。

首先固定C2=25，分别选取不同的C1，设计结果如表1所示。图3、图4给出了不同C1值下设计结果的开、闭环系统频域特性。

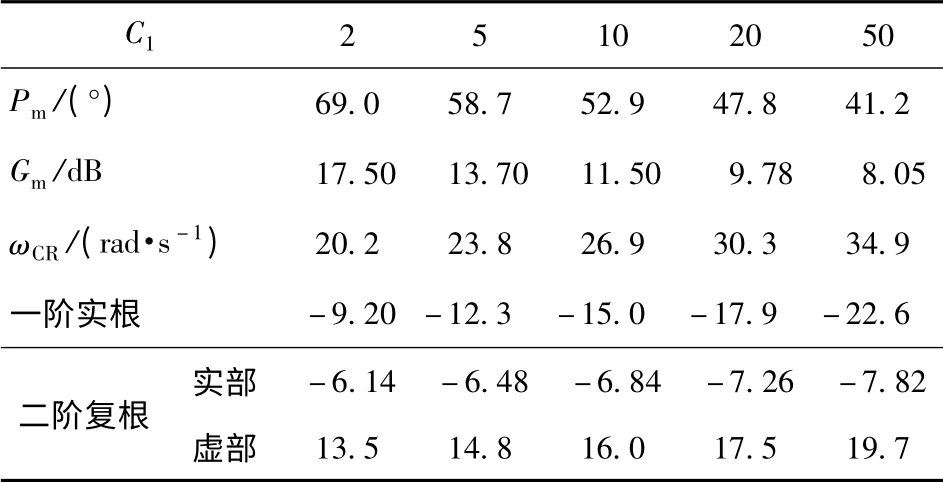
表1 不同C1下的设计结果Tab.1 Comparison of designs with different C1

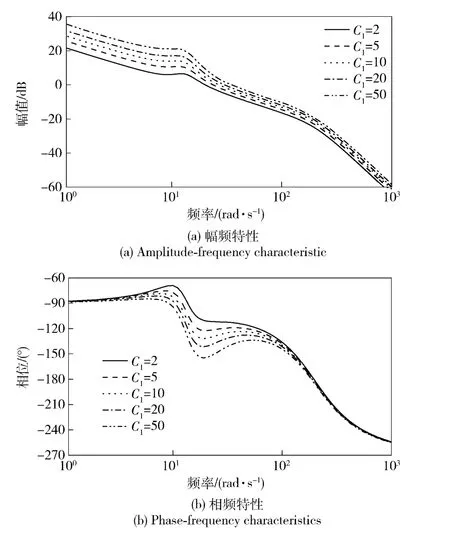
图3 不同C1值下设计结果的开环系统频域特性Fig.3 Bode diagram of open loop for different C1

固定C1=20，分别选取不同的C2，设计结果如表2所示。图5、图6分别给出了不同C2值下设计结果的开、闭环系统幅相频特性。

由表1设计结果可见，增大权系数C1，开环穿越频率和系统闭环带宽随之增大，主导极点远离虚轴，使系统的响应速度加快，在带宽附近处，闭环系统相位滞后略有减小，且在高频段的相位特性基本一致。但同时，系统幅相裕度有所减小，频域指标将会下降。

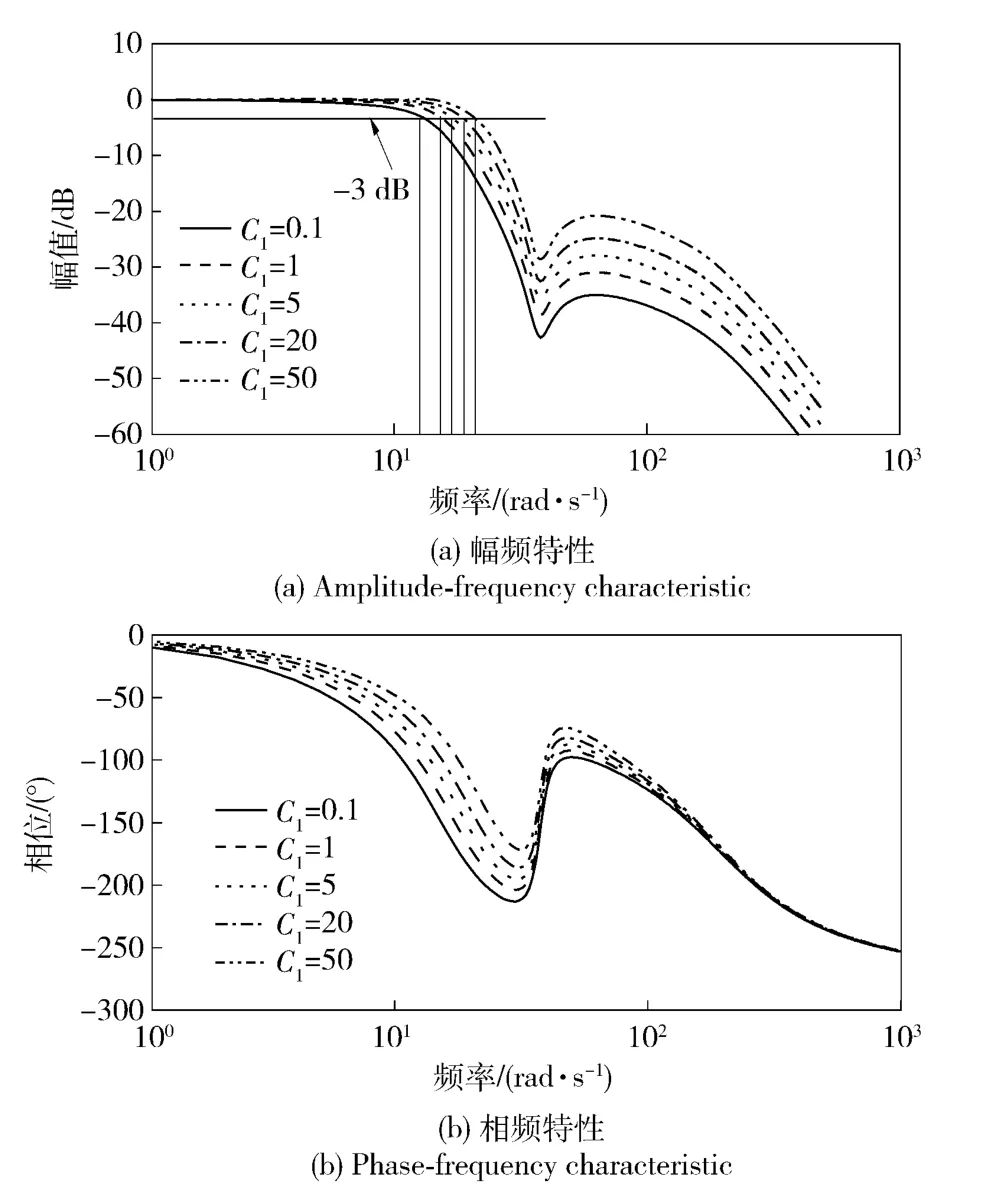
图4 不同C1值下设计结果的闭环系统频域特性Fig.4 Bode diagram of closed loop for different C1

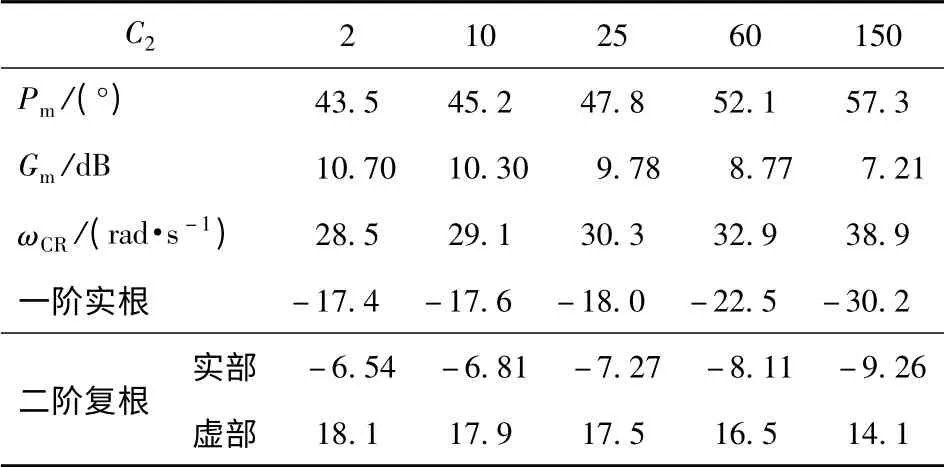
表2 不同C2值下的设计结果Tab.2 Comparison of designs with different C2

权系数C2主要影响系统的幅相裕度，由图5可见，增大C2，可提高相位裕度，但将减小幅值裕度。此外，C2对闭环系统带宽有一定影响，增大C2将减小系统带宽，而对闭环系统的相频特性影响甚微。

由最优理论设计的控制系统，可能出现满足相位裕度指标但穿越频率很大的现象。由于动力学模型仅考虑弹体与舵机环节，而系统纯延迟、惯性器件动力学、结构滤波器等都会带来相位滞后，直接威胁控制系统稳定性，因此，必须对开环穿越频率进行约束，以保证系统的稳定裕度［7］。

从图3和图5可看出，开环截止频率ωCR与C1关系密切。如图7所示给出了ωCR与C1的关系曲线。

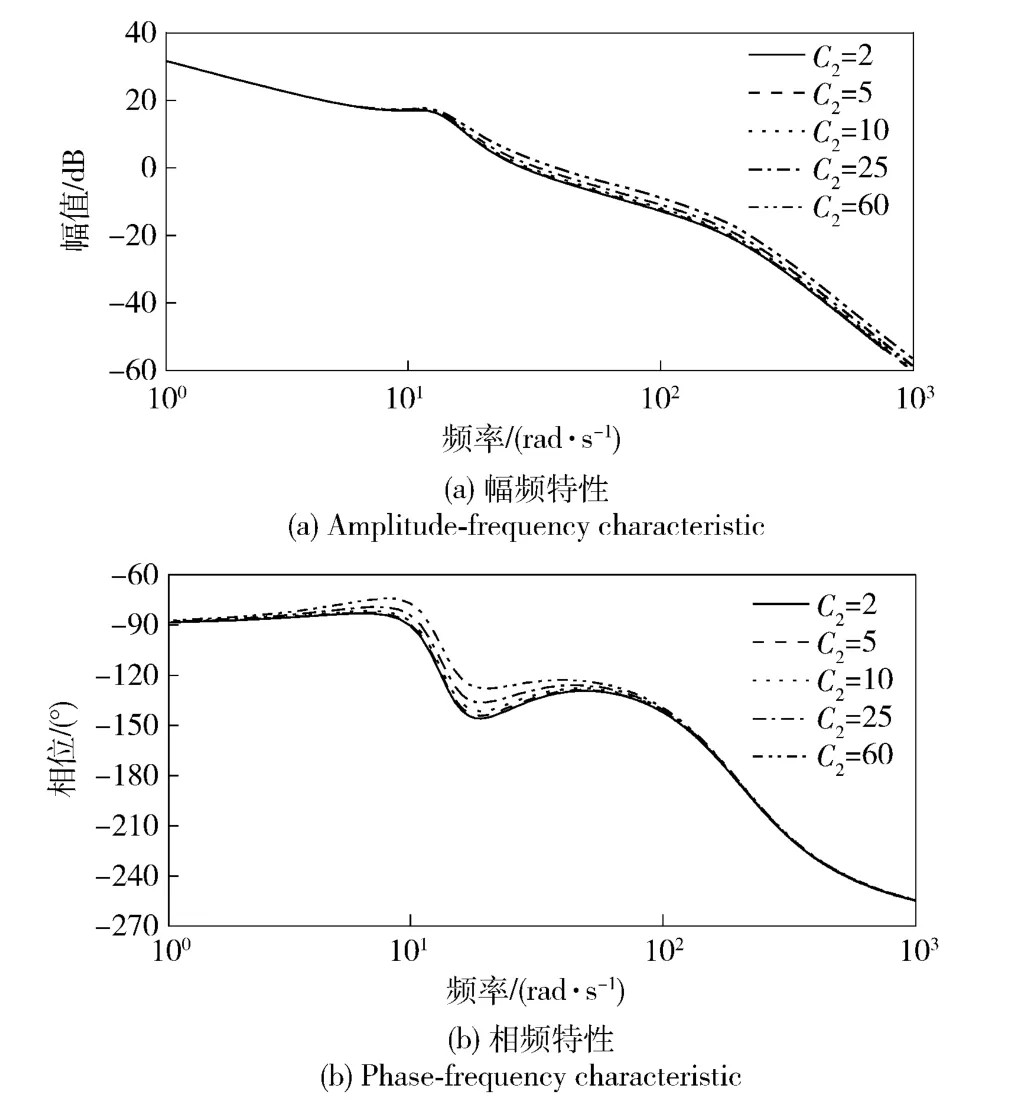
图5 不同C2值下设计结果的开环系统幅相频特性Fig.5 Bode diagram of open loop for different C2

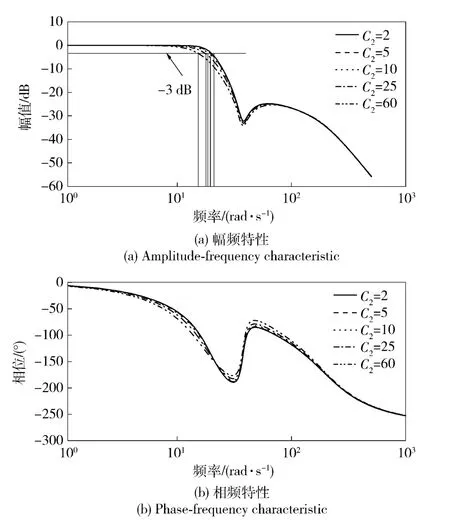
图6 不同C2值下设计结果的闭环系统幅相频特性Fig.6 Bode diagram of closed loop for different C2

设计者可根据ωCR与C1的关系，合理选取C1;综合考虑C1、C2系统与时域指标之间的关系调整权系数取值，使得到的控制器满足时域与频域的复合指标。最终选取C1=20，C2=25，C3=10 000. 由于俯仰、偏航动力学具有对称性，则采用SIMO 设计的反馈增益矩阵

式中:K1= [ 45 3.2 120 -220 0.41 ]×10-3.

若考虑耦合效应，则俯仰、偏航一体化数学模型为MIMO 系统，如(22)式所示。仍采用LQR方法设计控制律，称为MIMO 设计，示意图如图8所示。

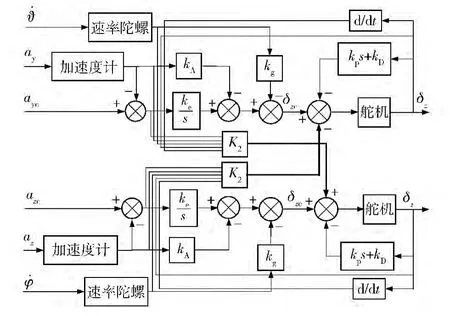
图8 MIMO 设计的控制系统示意图Fig.8 Control system designed via MIMO method

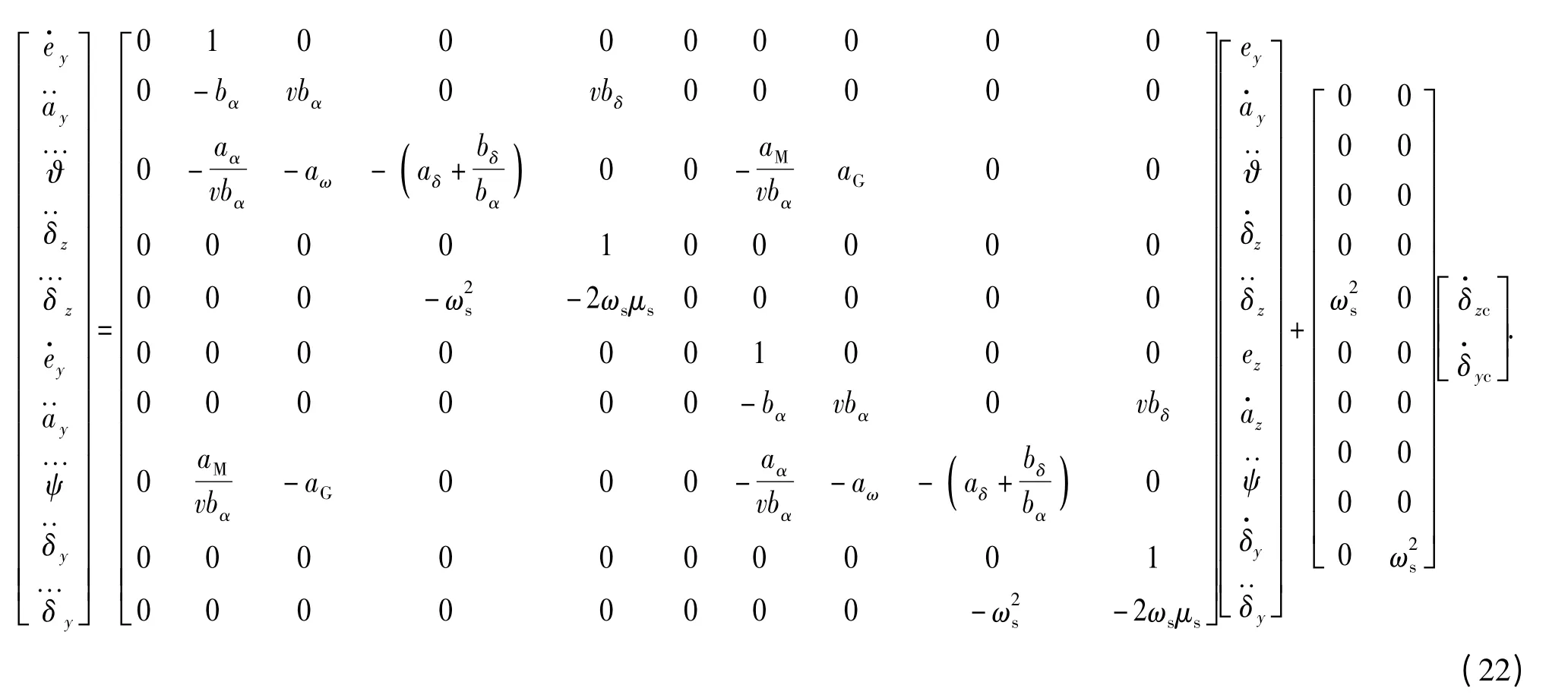
选取二次型性能指标函数为

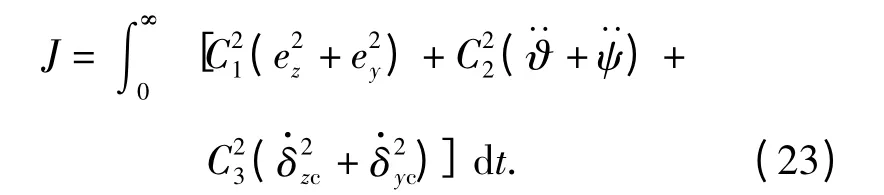
选取以单通道设计相同的权系数取值:C1=20，C2=25，C3=10 000，所得到状态反馈增益矩阵

式中:K1= [ 46 3.3 120 -230 0.43 ]×10-3;K2= [ 2.1 -0.2 4.2 21 0 ]×10-3.

反馈增益矩阵具有分块反对称的特点，通过多组设计结果对比两种设计方法，可归纳出:1)两个通道来源于自身通道反馈回路的控制参数K1差异很小;2)俯仰通道控制系统来自俯仰通道状态反馈的增益K1各元素，远大于来自偏航通道相应的增益K2各元素，偏航控制亦然;3)通道耦合使增益矩阵中的K2不为0，且耦合越大，则‖K2‖2越大。

滚转导弹的马格努斯效应和陀螺效应分别与静稳定力矩和阻尼力矩相对应，三回路驾驶仪中的过载反馈、角速率反馈人为增大了弹体静稳定系数和阻尼系数，使耦合效应在弹体姿态运动方程中所占的比重将有所减小，相对削弱了耦合效应的影响，从而使K2各元素远小于K1各元素。因此，滚转导弹存在的耦合效应对控制系统的设计结果影响不大，完全可以单通道独立设计。

4 数学仿真

为验证第3 节的设计结果与分析，建立存在通道耦合的数学仿真模型，各项气动参数为攻角、侧滑角的非线性函数，气动耦合项马格努斯力矩系数为静稳定力矩系数的40%，陀螺力矩系数为阻尼力矩系数的10%;引入角速率陀螺和加速度计的动力学环节，带宽均为40 Hz，阻尼系数为0.8. 在俯仰通道输入40 m/s2的阶跃过载指令，分别对不同C1、C2值下的设计结果进行仿真，俯仰、偏航通道过载响应分别如图9～图12 所示。

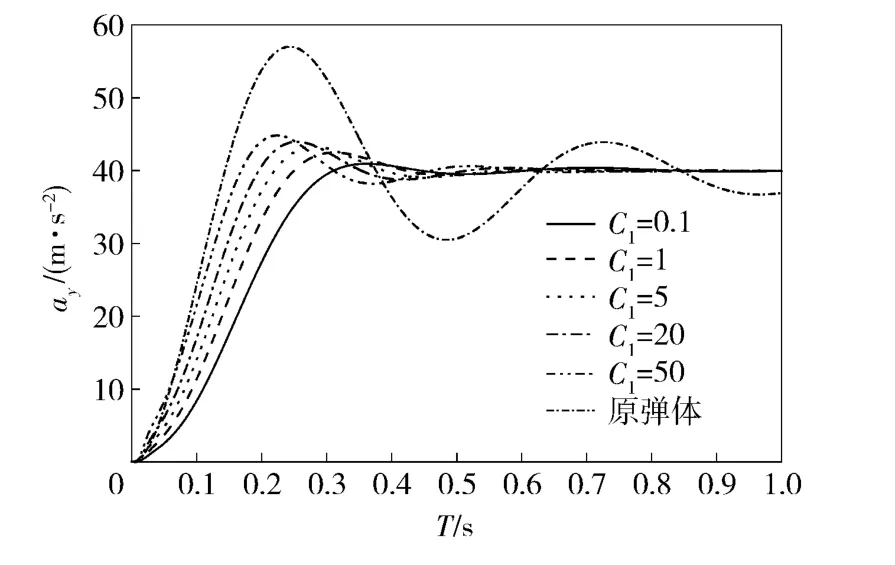
图9 不同C1值下设计结果的俯仰通道过载响应Fig.9 Response of pitch acceleration for different C1

图10 不同C1值下设计结果的偏航通道过载响应Fig.10 Response of yaw acceleration for different C1

由仿真结果可看出，与原弹体响应相比较，设计的控制系统使系统动态响应特性得以改善，且对耦合的抑制作用较为显著，可完全消除由耦合引起的响应稳态误差。增大权系数C1，可有效限制过载误差，加快系统响应速度;而权系数C2与超调量相关，增大权系数C2将减小系统超调。

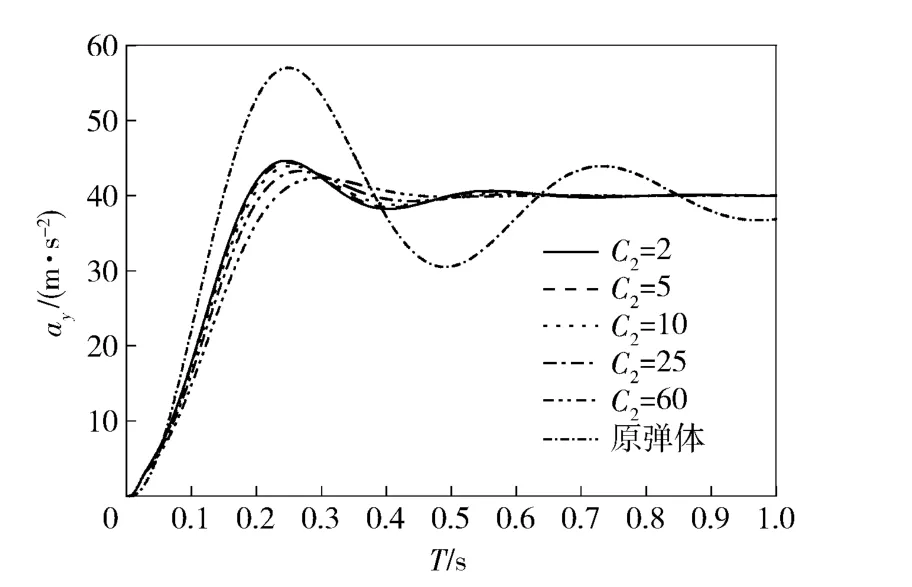
图11 不同C2值下设计结果的俯仰通道过载响应Fig.11 Response of pitch acceleration for different C2

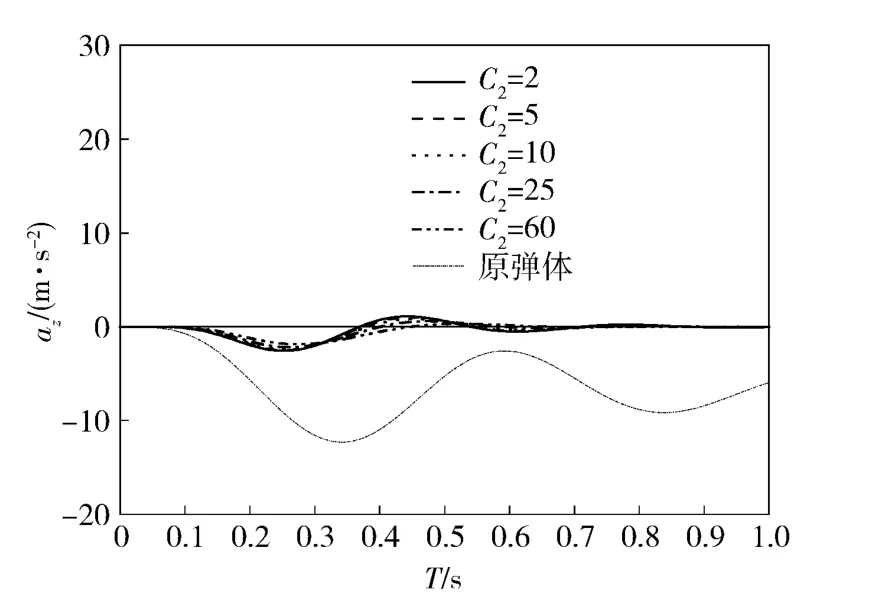
图12 不同C2值下设计结果的偏航通道过载响应Fig.12 Response of yaw acceleration for different C2

如图13 所示给出了本文SIMO 和MIMO 设计结果对俯仰通道阶跃过载指令的响应曲线。

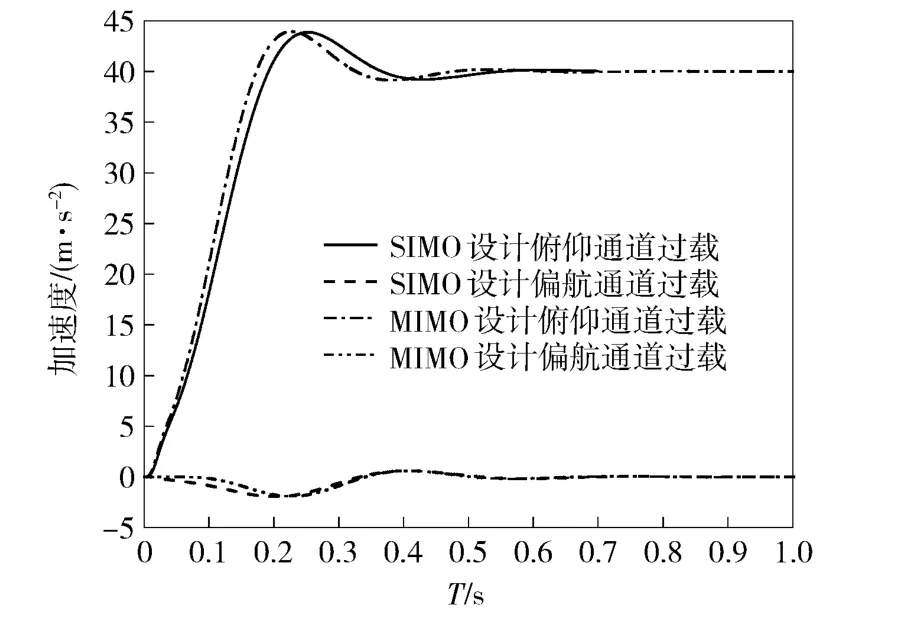
图13 两种设计结果的俯仰和偏航过载响应曲线Fig.13 Responses of pitch and yaw accelerations

由图13 可见，与SIMO 设计相较而言，MIMO 设计得到的控制系统在时域响应方面差异很小，在提高响应速度方面并不明显。且二者对耦合的抑制效果都十分理想，不存在稳态误差。作为Ⅰ型系统，三回路驾驶仪结构中的积分器可使由耦合运动造成的误差不断衰减，直至归0.

5 结论

通过对滚转导弹控制系统的设计与研究，本文应用LQR 理论提出了一种控制系统的设计方法，所得到的控制律具有三回路驾驶仪的结构;指出驾驶仪性能与权系数密切相关，通过对比不同权系数取值的设计结果，验证了权系数与驾驶仪的时频、频域性能之间的关系;SIMO 设计的三回路驾驶仪在抑制弹体耦合方面的效果十分理想，并具有良好的时域和频域性能，可使系统准确无误地跟踪阶跃指令，将耦合运动的稳态误差完全消除。最后，通过对比分析SIMO 设计和MIMO 设计，指出两种设计结果的差异很小。工程上，为滚转导弹设计三回路驾驶仪忽略状态耦合进行独立设计完全合理。最后，通过非线性数学仿真验证了以上结论。

References)

［1］Zarchan P. Tactical and strategic missile guidance［M］. Reston:AIAA，1997:507 -539.

［2］Garnell P. Guided weapon control systems［M］. 2nd ed. QI Zaikang Revision. Beijing:Beijing Institute of Technology，2004:162 -164.

［3］Lin D F，Fan J F，Qi Z K，et al. Analysis and improvement of missile three-loop autopilots［J］. Journal of System Engineering and Electronic，2009，20(4):844 -851.

［4］王辉，林德福，祁载康. 导弹伪攻角反馈的三回路驾驶仪分析［J］. 系统工程与电子技术，2012，34(1):92 -98.WANG Hui，LIN De-fu，QI Zai-kang. Design and analysis of missile three-loop autopilot with pseudo-angle of attack feedback［J］.Systems Engineering and Electronics，2012，34(1):92 -98. (in Chinese)

［5］温求遒，夏群力，祁载康. 三回路驾驶仪开环穿越频率约束极点配置设计［J］. 系统工程与电子技术，2009，31 (2):420 -423.WEN Qiu-qiu，XIA Qun-li，QI Zai-kang. Pole placement design with open-loop crossover frequency constraint for three-loop autopilot［J］. Systems Engineering and Electronics，2009，31(2):420 -423.(in Chinese)

［6］王嘉鑫，林德福，祁载康. 战术导弹三回路过载驾驶仪时频特性分析［J］. 兵工学报，2013，34(7):828 -834.WANG Jia-xin，LIN De-fu，QI Zai-kang. Analysis of tactical missile three-loop lateral acceleration autopilot in the time and frequency domain ［J］. Acta Armamentarii，2013，34 (7):828 -834. (in Chinese)

［7］Mracek C P，Ridgely D B. Missile longitudinal autopilots:connection between optimal control and classical topologies［C］∥AIAA Guidance，Navigation，and Control Conference. San Francisco:AIAA，2005:2005 -6381.

［8］Wise K A. A trade study on missile autopilot design using optimal control theory［C］∥AIAA Guidance，Navigation，and Control Conference. St Louis :AIAA，2007:2007 -6673.

［9］Nesline F，Zarchan P. Why modern controllers can go unstable in practice ［J］. Journal of Guidance，Control，and Dynamics，1984，7(3):495 -500.

［10］Williams D E，Friedland B，Madiwale A N. Modern control theory for design of autopilots for bank-to-turn missiles［J］. AIAA Journal of Guidance and Control，1987，10(4):378 -386.

［11］Shima T，Golan O M. Linear quadratic differential games guidance law for dual controlled missiles［J］. IEEE Transactions on Aerospace and Electronic System，2007，43(3):834 -842.

［12］Levy M，Shima T，Gutman S. Linear quadratic integrated versus separated autopilot-guidance design［J］. Journal of Guidance，Control，and Dynamics，2013，36(6):1722 -1730.

［13］Li K Y，Yang S X，Zhao L Y. Stability of spinning missiles with an acceleration autopilot［J］. Journal of Guidance，Control，and Dynamics，2012，35(3):774 -786.

［14］Li K Y，Yang S X，Zhao L Y. Three-loop autopilot of spinning missiles［J］. Journal of Aerospace Engineering，2014，228(7):1195 -1201.

［15］Burl J B. Linear optimal control ［M］. New Jersey:Prentice Hall，1996:183 -196.