基于分数阶傅里叶变换的线性调频引信定距方法
岳凯,郝新红,栗苹,陶艳,李永亮
(北京理工大学 机电学院,北京100081)
0 引言
传统双通道谐波定距调频(FM)引信的定距精度主要受调制频偏影响。调制频偏越大,定距精度越高。大的FM 频偏必然会带来大的寄生调幅和工程实现难题。因此,本文探索了一种新的FM 引信定距方法,以期在易于工程实现的调制频偏内获得较高的定距精度。参考现代数学成果在工程中的应用以及现代信号处理技术发展[1-2],分数阶傅里叶变换(FRFT)作为一种基于Chirp 基的正交分解算法,在处理连续波线性FM 信号方面具有天生的优势[3]。国内外很多学者展开了FRFT 在处理Chirp信号方面的研究[4-7],并取得了显著成果[8-13]。但将FRFT 研究成果应用于FM 引信实现其定距功能还未见报道。为此,本文提出了基于分数阶域瞬时初始频率估计和基于分数阶相关的两种线性FM 引信定距方法。
1 FRFT 及其离散算法
假设信号f(t)的角度α 的FRFT 表示为Fα(u),则FRFT 的定义式[13]为
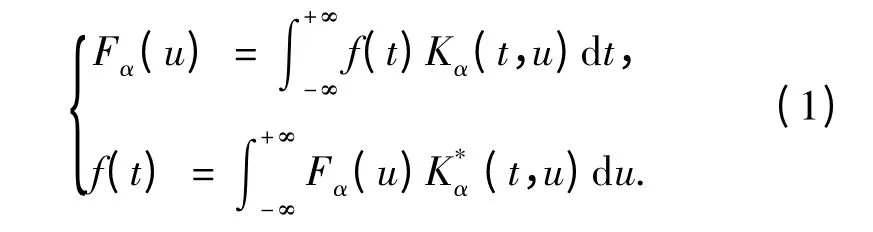
(1)式的变换核函数为

式中:α 为信号的Wigner 分布在时间-频率平面上投影的顺时针旋转角度,如图1所示。如果角度α或(α+π)为2π 的整数倍,那么核函数Kα(t,u)将会退化为δ(t-u)或δ(t+u).
图1中,坐标轴u 为相应的分数阶域坐标轴;fif(t)为线性FM 信号的瞬时频率曲线;IIF 为fif(t)在零时刻的值,即线性FM 信号初始频率;up为线性FM 信号在分数阶域的最优FRFT 阶次下能量聚集的坐标位置。根据FRFT 的性质[3],假设需处理的线性FM 信号与某一Chirp 基吻合,即在图1中变换角度其FRFT 的结果必定为u 轴上的一个有限冲激,且其分数阶域坐标为up.
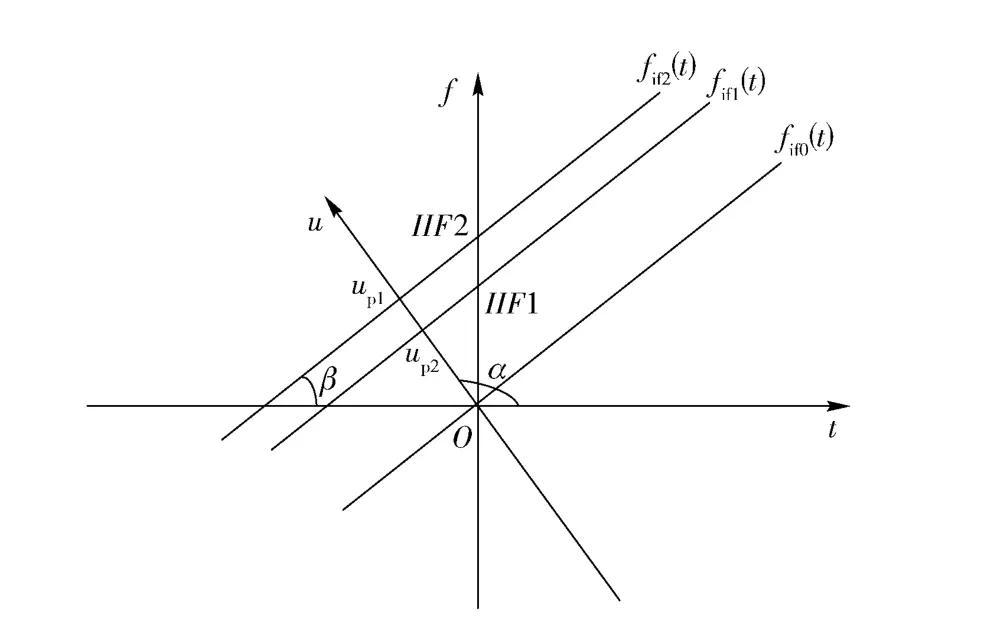
图1 定义在时频平面上的FRFTFig.1 The definition of FRFT on phase plane
为了便于工程上实现,FRFT 必须具有快速的离散算法。各国学者对离散FRFT 算法的研究已经取得了较多成果,提出了很多可行的算法,尤其是Ozaktas 的采样型算法,以速度快、精度高、具有与快速傅里叶变换(FFT)比拟的计算复杂度而受到广泛采用[14],其算法可表示为

2 基于分数阶域瞬时初始频率估计的FM引信定距方法
2.1 定距实现原理
基于分数阶域瞬时初始频率估计的FM 引信定距方法实现原理框图如图2所示。该方法的定距原理是利用线性FM 信号在特定角度(FM 率角度)的FRFT 为一冲激函数的性质,求取最优FRFT 阶次下发射与接收信号的FRFT 谱峰值在u 域的位置差,从而获得发射与接收信号的初始频率(如图1所示的IIF1 与IIF2),并通过初始频率差与时延估计的对应关系获得弹目间距离信息。由于该方法通过估计发射与接收信号的初始频率差得到时延估计值,且初始频率时变的,因此称该方法为瞬时初始频率估计。
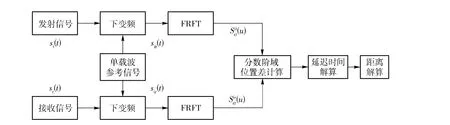
图2 基于分数阶域瞬时初始频率估计的定距方法原理框图Fig.2 Block diagram of the ranging method based on the initial frequency estimation in FRFT domain
首先,对FM 引信的发射信号和接收信号在射频端进行下变频,滤除载波频率,获得发射支路和接收支路的中频信号;而后,对两路中频信号进行固定α 角度的FRFT,因为对引信而言,中频信号的FM 率是已知的,所以变换角度其 中,K 为FM 率;再次,在固定α 角度的分数阶域搜索最大值点位置up,根据up求得瞬时初始频率;最后,根据瞬时初始频率与延迟时间的对应关系求得延迟时间,进而求得弹目距离。当弹目距离的估计值与预设的引爆距离相等时,给出引信点火信号。
假设FM 引信的调制信号为锯齿波,如图3所示,那么FM 引信发射信号可表示为
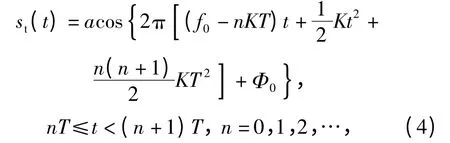
式中:a 为发射信号幅值;f0为信号中心频率;T 为调制信号周期;K =B/T 为调制信号的FM 率,B 为调制频偏。

图3 锯齿波FM 信号频率随时间变化图Fig.3 Instantaneous frequency of saw tooth wave
回波信号经目标反射后,相对于发射信号只是延迟了时间τ(t). 在实际引信应用中,每个运算周期内τ(t)的变换十分微小,可近似为常数,所以可将τ(t)在每个运算周期内看成是与时间t 无关的独立变量τ,因此单个周期内(后面出现的时域信号表达式均指单个周期之内的信号)的回波信号可表示为
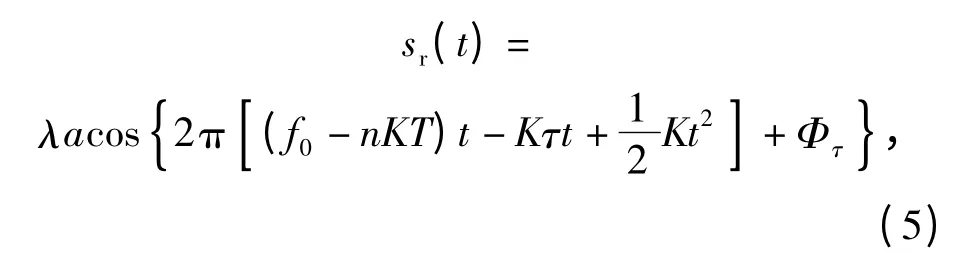
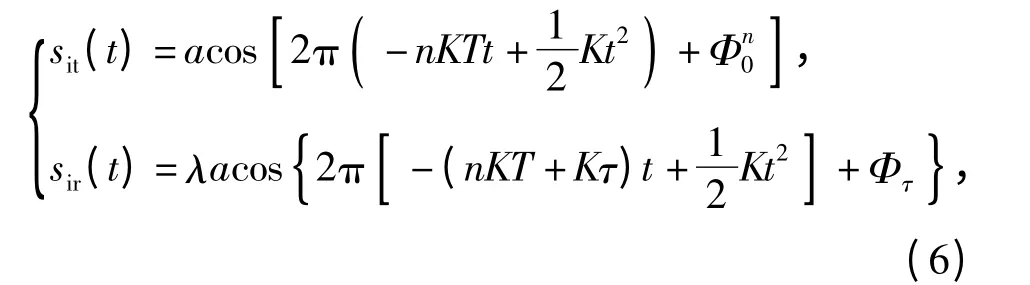
式中:Φ0n=πn(n+1)KT2+Φ0.
对两路中频信号的相位表达式求导,可得信号在零时刻的频率,即初始频率为
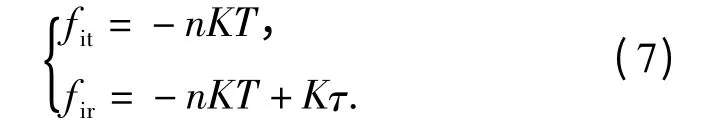
由于(7)式的初始频率是时变的,所以称之为瞬时初始频率。

结合(7)式、(8)式和cot α = -K,可获得延迟时间的估计

因此,根据关系式τ=2R/c,可获得弹目距离的估计值为

由(10)式可知,该方法可用于线性FM 引信的弹目距离估计。如果回波的延迟时间为固定值,则可进行预定距离的估计;如果回波延迟时间是动态变化的,则可实现连续测距功能。
2.2 定距方法性能分析
2.2.1 计算量分析
根据图2可知,要获得延迟时间估计,需同时估计两个中频信号的初始频率。该过程中只涉及到两路信号的FRFT,同时,中频信号的FM 率相对发射信号是不变的(即FM 率已知),所以只需进行固定角度的FRFT,无需在整个分数阶域扫描,大大减少了算法的计算量。由于FRFT 采用Ozaktas 的采样型离散算法[14],所以离散FRFT所需的乘法计算量为
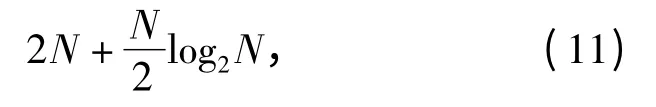
式中:N 为离散FRFT 的数据点数。其他部分所需的乘法运算次数相对(11)式可忽略。所以基于分数阶域瞬时初始频率估计的FM 引信定距方法所需的乘法计算量即如(11)式所示。
2.2.2 距离分辨力分析
由(10)式可知,该方法的固有距离分辨力决定于信号的时延分辨力,即决定于在α 阶分数阶傅里叶域up估计值的主瓣宽度。理想情况下,线性FM信号最优阶次的FRFT 的幅度谱是一个δ 函数,具有无限窄的主瓣宽度。文献[15]经由推导线性FM信号的FRFT 表达式已证明此点。因此,固有距离分辨力是无穷小,即对具有任意延迟时间差异的两个信号,该方法可以分辨。
实际工程应用中,采用离散方法求取弹目间距离估值时,该方法的距离分辨力还受到信号重复周期数及采样点数的影响。因为在有限观测时间Td内,线性FM 信号分数阶域傅里叶变换的积分区间为观测区间,可证明其在最优阶次FRFT 的幅度谱由冲激函数演化为sinc 函数,且分数阶域up估计值的-3 dB 主瓣宽度[16]。
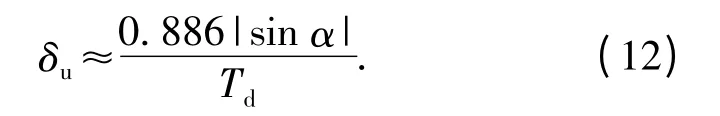
考虑距离估计值来自离散采样集合{us,2us,…,Nus},其中,us为最优阶次分数阶域离散步长。设定观测区间Td=mT,将(12)式带入(10)式可得该方法的距离分辨力为
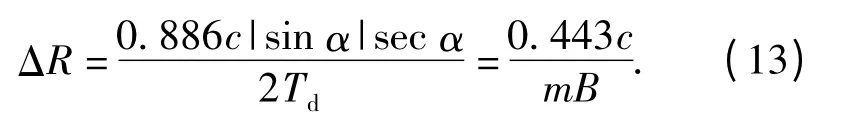
设定采样频率为fs(fs≥2B,满足采样定理),采样点数为N,则距离分辨力可表示为
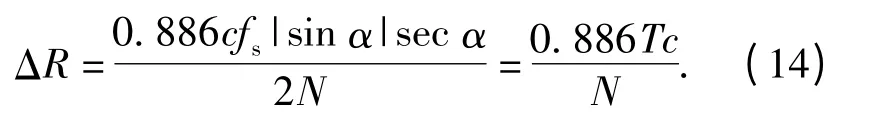
(13)式与(14)式为距离分辨力的两种不同表述方式。由(13)式、(14)式可知,该方法的距离分辨力主要受信号带宽B、运算周期数m、调制周期T、运算点数N 等参数影响。为了提高距离分辨力,在不增加调制带宽的条件下,只需增加运算点数或减小调制周期即可。相对于谐波定距FM 引信增大调制频偏来提高距离分辨力的方法,这种方法更容易实现,且可提高定距引信的精度。
此外,由(13)式可知,当运算周期m =1 时,该方法的时延分辨力约为1/B,即距离分辨力约为c2B,等效于FM 谐波定距方法的定距精度。
3 基于分数阶相关的FM 引信定距方法
3.1 定距实现原理
基于分数阶相关的FM 引信定距方法实现原理如图4所示。分别对参考信号(发射信号)和回波信号进行下变频,获得中频信号;参考信号的中频信号延迟特定时间(该时间与引信预定作用距离相对应);对延迟后的参考信号的中频信号与回波信号的中频信号进行离散FRFT;变换后的两路信号相乘并累加,获得两路信号的相关信号;对相关信号进行阈值检测,满足条件时即可获得预定距离处的点火信号。
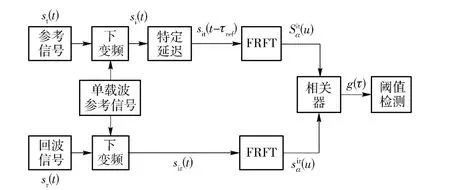
图4 基于分数阶相关的FM 引信定距方法原理框图Fig.4 Block diagram of the ranging method based on the fractional correlation
假设FM 引信以锯齿波为调制信号,那么以(4)式发射信号作为参考信号,(5)式为回波信号,参考信号和回波信号通过与单载波信号x(t)=cos(2πf0t)混频进行下变频,并对下变频后的发射信号做固定延迟τref,获得两路中频信号为

分数阶相关等价于对信号做FRFT,再在分数阶域进行一般意义的相关运算,因此其数学表达式[3]可表示为

对(16)式取模,可得相关峰函数为

设x(t)为要检测的目标信号,输入信号s(t)=x(t-τ0),参考信号h(t)=x(t -τref),对(17)式求导并令其等于0,可得到分数阶相关峰的位置为
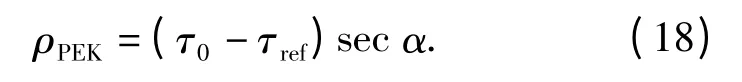
本方法所用的分数阶相关与如上所述的分数阶相关并不完全相同,而是采用先延迟,而后进行FRFT,再求取内积的计算方法。如图4所示,本方法中相关输出可定义为
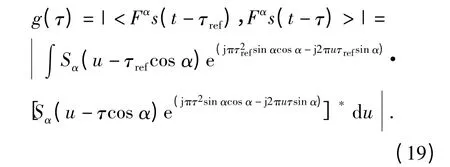

式中:up为分数阶s(t-τref)的FRFT 所得的有限冲激函数在分数阶域的位置。
最后,对(20)式所示的相关函数做阈值检测,当满足阈值条件时,给出点火信号。
该方法是一种基于发射信号支路固定延迟的定距方案,故可用于预定距离估计,不能用于连续估计瞬时距离。
3.2 定距方法性能分析
3.2.1 计算量分析
根据(15)式的中频信号和(4)式的发射信号表达式,可知FM 率是保持不变的,即中频信号的FM 率是已知的。因此,只需对中频信号进行固定角度的FRFT,相对于阶数搜素的算法可大大减少运算复杂度。
为了获得一个相关值,首先需对两个中频信号分别进行FRFT,由于方法中的FRFT 采用的是Ozaktas的采样型离散算法[14],故进行FRFT 的乘法计算量为完成FRFT 后,需对N 点的变换结果进行乘累加(即相关运算),其乘法计算量为N. 故计算一个相关值所需的乘法计算量为

3.2.2 检测概率分析
假设系统输入噪声为高斯噪声,由于FRFT 是一种线性变换,所以输出的噪声仍然服从高斯分布。设其均值和方差分别为un和σ2n,设检测门限为λ.根据检测理论,在贝叶斯准则下的检测概率PD和虚警概率PF分别为
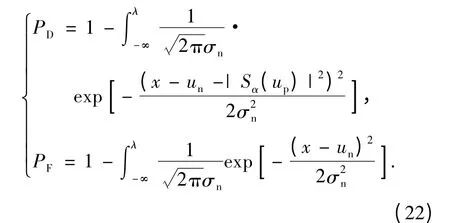
3.2.3 距离分辨力分析
由(19)式和(20)式可知,该方法的定距原理基于信号在最优阶次下分数阶傅里叶域up的估值,获得弹目距离估计。本文定义的分数阶相关函数在分数阶域也是一个δ 函数,具有无限窄的主瓣宽度,所以延迟时间估计的理论分辨力无穷小,即对具有任意延迟时间差异的两个信号,该算法是可分的。
因此,本质上该方法的距离分辨力等同于第一种方法。当采用离散方法求取弹目间距离估值时,该方法的距离分辨力同样会受到信号重复周期数及采样点数的影响。这里不再赘述。
与瞬态初始频率估计方法不同的是,其利用分数阶域幅度谱的模平方求取谱峰值(如(20)式所示),而前者是利用幅度谱的模求取谱峰值。
4 仿真与讨论
本文分别对两种方法进行了Matlab 仿真来验证其可行性与测距性能。
仿真参数如下:FM 带宽B =30 MHz,调制周期T=166 μs,弹目交会距离取[25 m,50 m]. 当运算周期为一个调制周期时,则距离分辨力约5 m.
分别设定引信的预定起爆距离为35 m、40 m、45 m,基于分数阶相关方法和基于瞬时初始频率估计方法的预定起爆距离估计仿真结果分别如图5和图6所示。
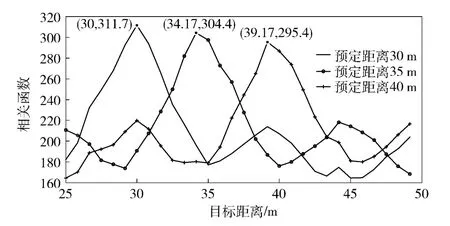
图5 不同预定距离条件下中频信号的分数阶相关函数Fig.5 Fractional correlation of the intermediate frequency signal under the conditions of different fixed distances
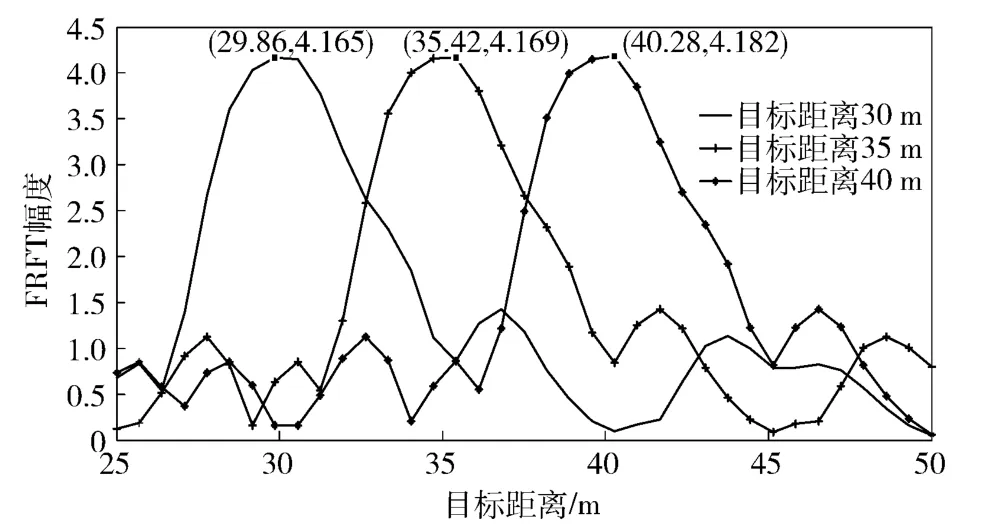
图6 不同距离处中频信号的FRFTFig.6 Fractional Fourier transform of the intermediate frequency signal at different distances
由图5与图6可知:引信3 个预定的起爆距离分别对应于最优阶次下的分数阶域相关函数峰值与中频信号的FRFT 谱峰值,证明了两种定距方法的可行性;当运算周期为一个调制周期时,两种方法谱峰值下降-3 dB 时对应的主瓣宽度为5 m,即图5相关函数峰值与图6FRFT 幅度谱峰值下降1/2 时所对应的主瓣宽度,与理论距离分辨力相吻合。
为了分析两种方法的抗噪声性能,分别对两种方法进行了不同信噪比(-20 ~20 dB)条件下的1 000点蒙特卡洛仿真实验。设定引信预定起爆距离为40 m,加载的噪声类型为高斯白噪声,其他仿真参数同上,不同信噪比下两种方法蒙特卡洛实验方差与均值的仿真结果分别如图7和图8所示。

图7 不同信噪比条件下两种算法的1 000 点蒙特卡洛仿真实验结果(方差)Fig.7 Results of 1 000 points Monte-Carlo simulation at different SNRs(variance)

图8 不同信噪比条件下两种算法的1 000 点蒙特卡洛仿真实验结果(均值)Fig.8 Results of 1 000 points Monte-Carlo simulation at different SNRs
对比分析图7、图8:信噪比大于0 dB 时,两种方法均具有良好的抗噪声性能;当信噪比小于0 dB时,初始频率估计方法抗噪性能急剧恶化。仿真结果说明,分数阶相关方法抗噪声性能优于初始频率估计方法,更适合于低信噪比环境下(如强背景噪声干扰)信号检测。
分析调制频偏、运算点数等参数对距离分辨力的影响,其仿真结果如图9所示,其中采样率为10 倍调制频偏,其他参数:调制频偏10 ~50 MHz,运算点数100 ~5 000,调制信号频率600 kHz.

图9 调制频偏和运算点数对距离分辨力影响Fig.9 Influences of the modulation frequency derivation and operation points on range resolution
图9仿真结果表明:分数阶域瞬时初始频率估计的定距方法在有限增加的调制频偏内(受限于探测器调制带宽与体积约束),增加运算点数可显著提高引信的距离分辨力。
将cot α= -K,K=B/T 代入(14)式,可得
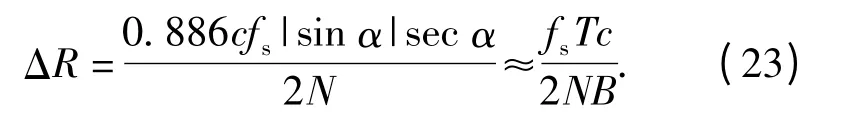
(23)式表明:增加调制频偏与运算点数可显著提高引信的距离分辨力;若取采样频率为10 倍调制频偏,则引信距离分辨力与运算点数呈反比。该结论与图9的仿真结果相吻合。该结论同时表明,引信在不增大调制频偏的前提下,通过稍微加大运算点数的方法可显著提高其距离分辨力。
固定调制频偏,取仿真参数为:调制频偏30 MHz,运算点数250、700、1 200,采样率10 倍调制频偏,调制信号频率600 kHz.
根据(14)式,在采样率为10 倍调制频偏的条件下可计算出距离分辨力,如表1所示。

表1 距离分辨力对比仿真结果Tab.1 Comparison of range resolutions of different ranging methods
表1结果表明:在相同的调制信号参数条件下,运算点数无需太大,两种方法的定距性能优于传统的双谐波定距方法。
图10 为仿真了运算点数为1 200 点情况下,不同距离处目标的FRFT. 由图10 可知,30 m 处与30.5 m 处目标不可分辨,而与32 m、35 m 处目标峰值可区分,证明该运算点数下距离分辨力约2 m.
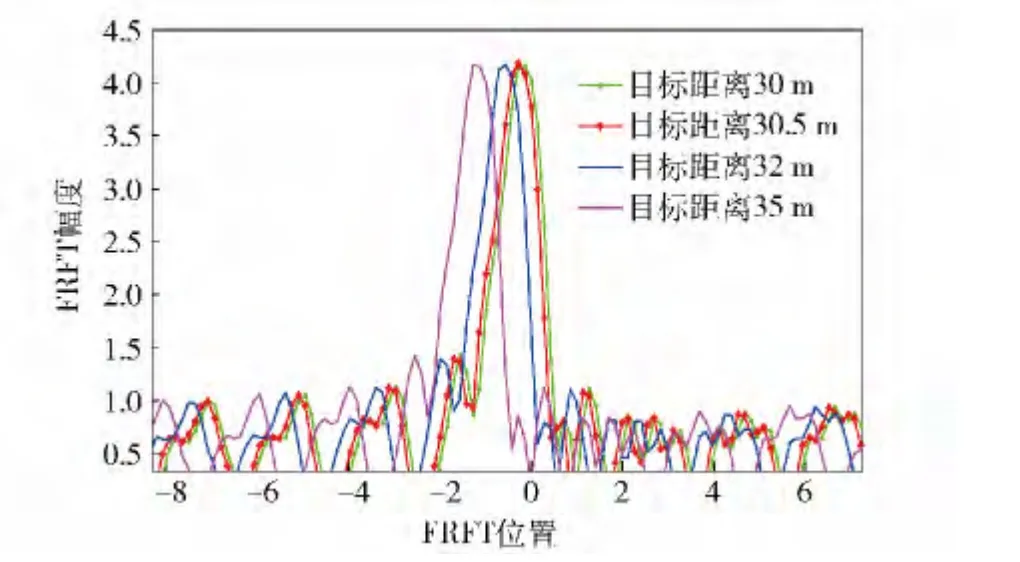
图10 运算点数为1 200 点时不同距离处目标回波中频信号的FRFTFig.10 FRFT of the intermediate frequency signals at different distances with calculation points of 1 200
图11 为仿真了700 点运算点数的情况下,不同距离处目标的FRFT. 从中可见,30 m 与30.5 m、32 m 处的目标不能区分,而32 m 与35 m 处目标可分辨,证明距离分辨力约3 m. 仿真结果与理论计算距离分辨力相吻合。
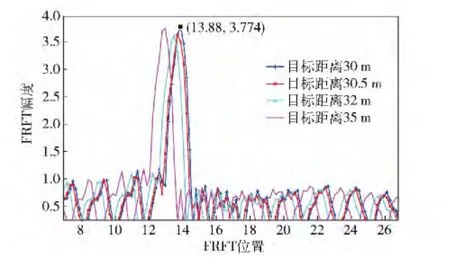
图11 运算点数为700 点时不同距离处目标回波中频信号的FRFTFig.11 FRFT of the intermediate frequency signals at different distances with calculation points of 700
最后,仿真了0 dB 高斯白噪声背景下,分数阶域瞬时初始频率估计方法的动态测距性能,仿真结果如图12 所示,估计值与理想值吻合较好,证明了该定距方法的可行性。
5 结论
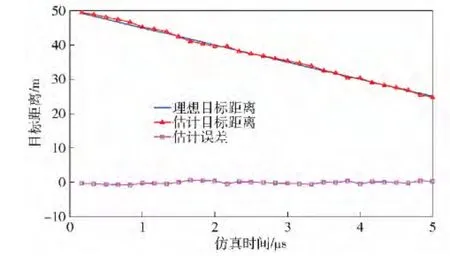
图12 0 dB 信噪比时目标距离估计仿真结果Fig.12 Simulation results of target range estimation for SNR=0 dB
本文提出了基于分数阶域瞬时初始频率估计和基于分数阶相关的FM 引信定距方法。理论推导了两种方法的定距原理,仿真证明了两种方法的可行性。在定距性能方面,两种方法的距离分辨力相同,在相同的调制频偏条件下只需不大的运算点数,其定距精度就可超过传统的双谐波定距方法;在算法计算量上,由于两种方法均利用了回波信号FM 率,已知这一先验条件,避免了对最优FRFT 阶数的搜索,使计算量控制在与FFT 相当的水平,满足工程应用的要求。此外,基于分数阶域瞬时频率估计的FM 引信定距方法可实现连续测距功能,可用于引信高度表或具有炸高精确分档的引信。
References)
[1]Namias V. The fractional order Fourier transform and its application to quantum mechanics[J]. Ima Journal of Applied Mathematics,1980,25(3):241 -265.
[2]张贤达,保铮. 非平稳信号分析与处理[M]. 北京:国防工业出版社,1998.ZHANG Xian-da,BAO Zheng. Non-stationary signal analysis and processing[M]. Beijing:National Defense Industry Press,1998.(in Chinese)
[3]陶然,齐林,王越. 分数阶Fourier 变换的原理与应用[M]. 北京:清华大学出版社,2009.TAO Ran,QI Lin,WANG Yue. Theory and application of fractional Fourier transform[M]. Beijing:Tsinghua University Press,2009. (in Chinese)
[4]温景阳,张焕宇,王越. 线性调频脉冲压缩雷达信号参数估计方法[J]. 北京理工大学学报,2012,32(7):746 -750.WEN Jing-yang,ZHANG Huan-yu,WANG Yue. Parameters estimation algorithm of LFM pulse compression radar signal [J].Transactions of Beijing Institute of Technology,2012,32(7):746 -750. (in Chinese)
[5]马艳,罗美玲. 基于分数阶傅里叶变换水下目标距离及速度的联合估计[J]. 兵工学报,2011,32(8):1030 -1035.MA Yan,LUO Mei-ling. FRFT-based joint range and radial velocity estimation of underwater target[J]. Acta Armamentarii,2011,32(8):1030 -1035. (in Chinese)
[6]邓兵,王旭,陶然,等. 基于分数阶傅里叶变换的线性调频脉冲时延估计特性分析[J]. 兵工学报,2012,33(6):764 -768.DENG Bing,WANG Xu,TAO Ran,et al. Performance analysis of time delay estimation for linear frequency-modulated pulse based on fractional Fourier transform [J]. Acta Armamentarii,2012,33(6):764 -768. (in Chinese)
[7]邓兵,陶然,董云龙. 基于分数阶傅里叶变换的标量脱靶量测量新方法[J]. 兵工学报,2010,31(12):1627 -1631.DENG Bing,TAO Ran,DONG Yun-long. New method for scalar miss distance measurement based on the fractional Fourier transform[J]. Acta Armamentarii,2010,31(12):1627 -1631. (in Chinese)
[8]Ozaktas H M,Barshan B,Mendlovic D,et al. Convolution,filtering,and multiplexing in fractional Fourier domains and their relationship to chirp and wavelet transform[J]. Journal of the Optical Society of America A,1994,11(2):547 -559.
[9]Ozaktas H M,Aytur O. Fractional Fourier domains[J]. Signal Process,1995,46(1):119 -124.
[10]Ozaktas H M,Zalevsky Z,Kutay M A. The fractional Fourier transform with applications in optics and signal processing[M].New York:Wiley,2000:1 -513.
[11]Olcay A. Fractional convolution and correlation via operator methods and an application to detection of linear FM signals[J].IEEE Transactions on Signal Processing,2001,49(5):979 -993.
[12]Akay O. Unitary and Hermitian fractional operators and their extension:fractional Mellin transform,joint fractional representations and fractional correlations [D]. Kingston:University of Rhode Island,2000.
[13]Almeida L B. The fractional Fourier transform and time-frequency representations [J]. IEEE Transactions on Signal Process,1994,42(11):3084 -3091.
[14]Ozaktas H M,Arikan O,Kutay M A,et al. Digital computation of the fractional Fourier transform [J]. IEEE Transactions on Signal Process,1996,44(9):2141 -2150.
[15]张淑宁,赵惠昌,吴兵. 基于分数阶傅里叶变换的伪码体制引信线性调频干扰抑制技术[J]. 兵工学报,2006,27(1):32 -36.ZHANG Shu-ning,ZHAO Hui-chang,WU Bing. LFM interference excision technique in pseudo random code fuse based on fractional Fourier transform[J]. Acta Armamentarii,2006,27(1):32 -36.(in Chinese)
[16]张南,陶然,单涛,等. 基于分数阶傅里叶变换的线性调频信号分辨率分析[J]. 电子学报,2007,35(12A):8 -13.ZHANG Nan,TAO ran,SHAN Tao,et al. Analysis of the resolution of the linear frequency modulated signal based on the fractional Fourier transform[J]. Acta Electronica Sinica,2007,35(12A):8 -13. (in Chinese)

