基于恒星几何构型分布的天文定位误差建模及误差特性分析
赵慧,熊智,王丽娜,潘加亮,郁丰,戴怡洁
(1. 南京航空航天大学 自动化学院,江苏 南京210016;2. 北京航天自动控制研究所 宇航智能控制技术国家级重点实验室,北京100854;3. 南京航空航天大学 航天学院,江苏 南京210016)
0 引言
天文导航是以已知准确空间位置、不可毁灭的自然天体为基准,并通过光电和射电方式被动探测天体位置,经解算确定测量点所在载体的经度、纬度、航向和姿态等信息[1-2]。天文导航系统具有自主性强、可靠性高、精度好等优点,一直受到各军事强国的重视[3],已经成为组合导航系统的重要组成部分,广泛应用于舰艇、飞机、空间飞行器等领域[4]。
目前,对天文定位性能的研究多集中于提高天文敏感元件性能的研究[5-6]。为提高天文敏感器的测量性能,恒星星光的敏感器元件由CCD 向CMOS发展[7];为降低杂散光对天文敏感器性能的影响,敏感器遮光罩由单节型向优化的两节型遮光罩发展[8];为降低敏感器畸变及色差,对敏感器镜头进行像方远心化等结构优化并引入二元光学面[9]。
在天文定位选星过程对天文定位误差特性研究方面的文献较少。文献[10 -11]给出了一般性的恒星选择标准,其认为双星定位时,恒星方位角应在60° ~120°之间,以趋近90°最好;三星定位时,三星分布范围要在180°以上,相邻星体间方位角趋近120°最好,对于具体的理论依据,并未进行深入研究,尚无法给出基于天文观测恒星几何构型选星的理论依据。
为此,本文从天文定位基本原理出发,推导建立了天文定位误差模型,以此为基础,分析了影响天文定位精度的因素。在此基础上,着重研究了恒星几何构型分布中恒星方位角对天文定位的影响规律,并给出了判别恒星几何构型中恒星方位角优劣的条件,为有效提高天文定位性能提供了理论参考依据。
1 天文定位误差建模
天文定位的基本原理是通过观测恒星的高度角和方位角进行定位的[12-13]。基于天文恒星观测的天文定位基本原理如图1所示。
图1中,K 点为载体所在真实位置,C 为推算的载体位置,GP为观测恒星的星下点。PNK、PNGP分别为过载体位置K 和恒星星下点GP的子午线,则为星下点相对于载体位置的方位线90° -h,h 即为观测恒星的高度角,∠PNKGP为观测恒星的方位角A. 恒星星下点相对于推算的位置点C 的方位线则方位线即为恒星高度与载体推算高度之间的高度差值Δh. 在天文定位过程中,通过天文敏感器,载体可测得恒星的高度角h 和方位角A,由推算的位置点C 可计算得到该恒星的计算高度角hc,从而得到高度差Δh 即方位线
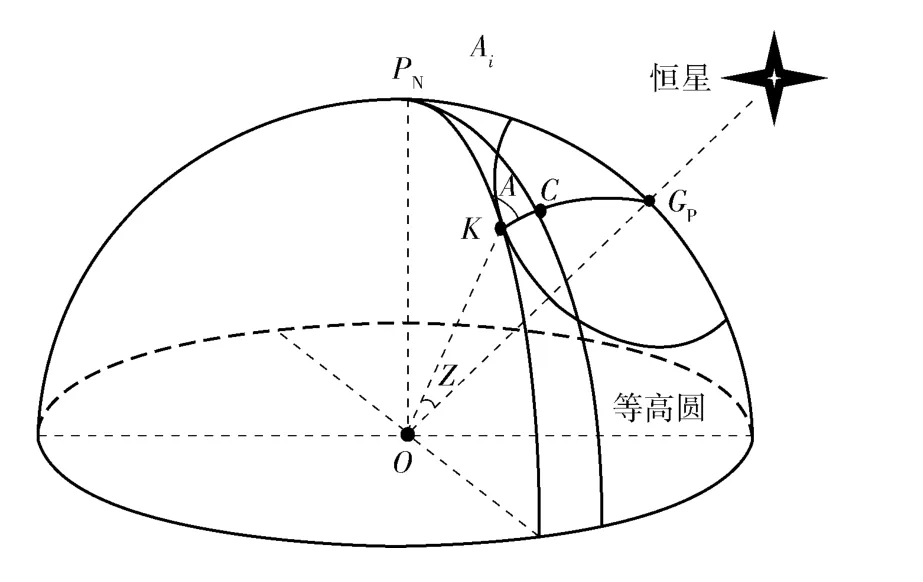
图1 天文定位原理图Fig.1 Schematic diagram of celestial positioning
以K 点为原点,东西向为x 轴,南北向为y 轴,建立如图2所示的示意图。
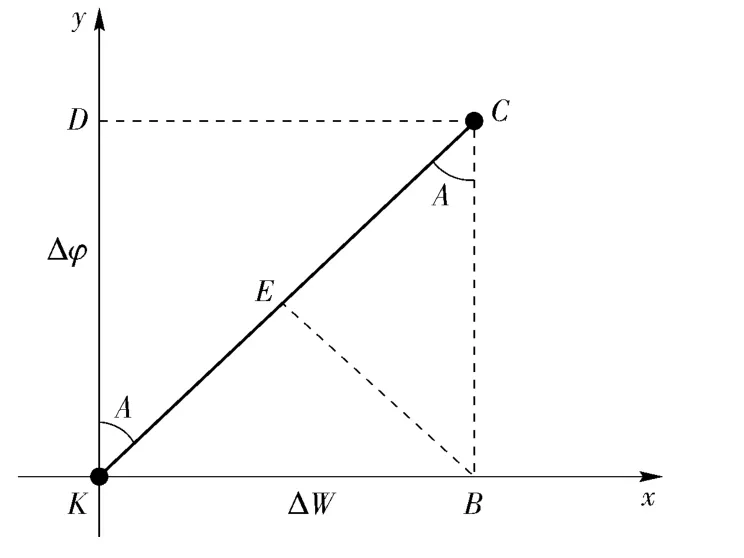
图2 计算载体位置示意图Fig.2 Position calculation of vehicle
根据图2,可以获得高度差的基本计算公式[14]如下:

式中:Δφ 为纬度误差(即南北方向距离);ΔW =cos φ·Δλ(即东西方向距离),Δλ 为经度误差。
当可观测恒星数目大于1 时,根据(1)式可得多颗导航恒星观测时的矩阵描述,即


当推算位置点为载体的实际位置时,高度差ΔH 即为测量误差,不同恒星间的测量误差互不相关。则有天文定位误差协方差为
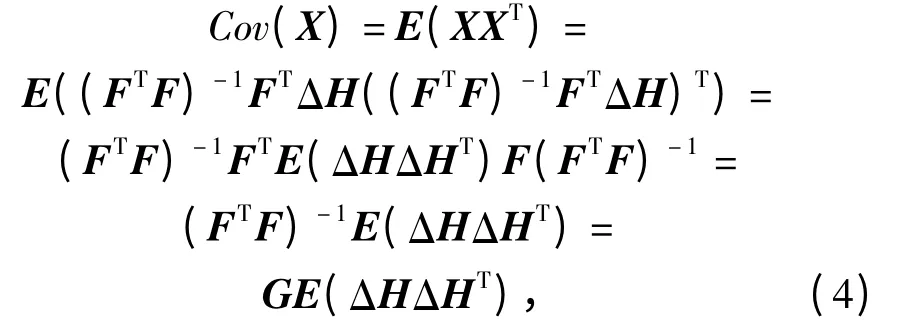
式中:矩阵G 定义为

由(5)式可知,G 为2 ×2 的对称矩阵。其中,m定义为

(4)式清晰地表明了高度差方差经由矩阵G 转换为定位误差的方差。根据(4)式可知,天文定位精度与以下两方面因素有关:
1)测量误差:恒星高度角测量误差的方差越大,定位误差X 的方差就越大。
2)恒星的几何构型:矩阵G 取决于导航恒星的个数以及各个导航星的方位角。矩阵G 中的元素越小,则由测量误差转换为定位误差的程度就越低。
2 恒星几何构型对天文定位性能影响分析
2.1 基于恒星几何构型的天文定位误差模型
从第1 节的分析可以看出,在天文敏感器选定的条件下(高度角测量误差一定),天文定位误差主要受到恒星几何构型分布的影响。为此,记恒星高度角测量误差方差为σ2h,则由(4)式得
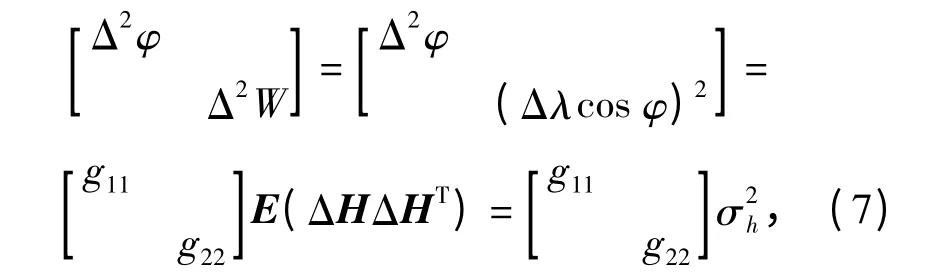
式中:g11和g22为系数阵G 的对角线元素。根据(5)式可得,g11=从而可以根据均方误差分析定位精度:

下面将以天文导航中常用的双星观测和三星观测为例,分析恒星几何构型中恒星方位角对天文定位性能影响。
2.2 双星观测几何构型下的天文定位误差特性分析
首先分析双星观测条件下的定位性能,根据(6)式可得

则天文定位均方误差为
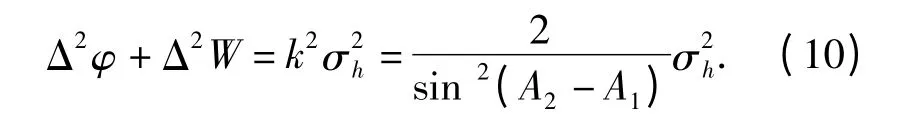
即双星观测条件下天文定位误差特性满足(10)式. 由于A1,A2∈[0,2π],因而|A2-A1|∈[0,2π]. 由(10)式可知,在天文敏感器精度一定的情况下,天文定位误差仅和导航星方位角之差A2-A1有关。当两颗导航星方位角之差为90°或者270°时,m2值最大,此时误差权系数因此,当两颗导航星方位角之差接近90°或者270°时,双星天文定位性能较优。
为形象描述恒星几何分布中恒星方位角对天文定位性能的影响,下面从几何角度进行分析。图3给出了双星观测条件下天文定位误差与恒星方位角之间的关系示意图。
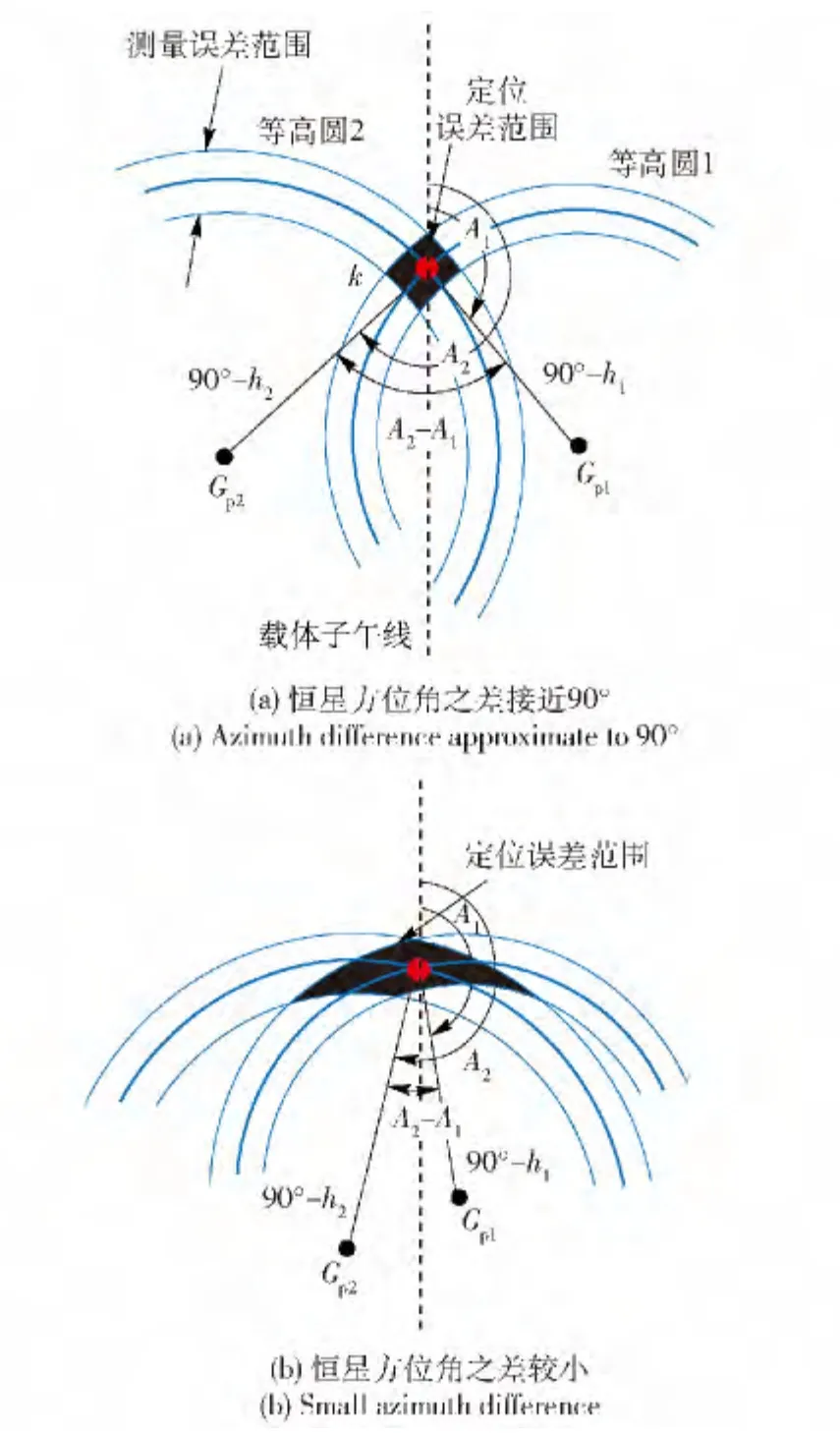
图3 双星观测条件下天文定位误差与恒星方位角之间关系Fig.3 Relationship between positioning error and azimuth under double-star observing condition
图3中粗实线以恒星星下点GP为圆心,恒星顶距为半径的等高圆圆弧,两条细圆弧表示恒星高度角的测量误差。载体真实位置为两条粗实线的交点K,虚线为载体所在位置子午线。由载体子午线至方位线Gp1K 的夹角A1为恒星1 的方位角,由子午线至方位线Gp2K 的夹角A2为恒星2 的方位角,而阴影部分代表由高度测量误差造成的定位结果可能的范围。
从图3(a)中可看出,当观测的导航恒星方位角之差接近90°时,两个等高圆相交的阴影部分面积小而集中;从图3(b)中可看出,当观测的导航恒星方位角之差较小时,即两颗导航星相对于载体而言差不多处于同一个角度,此时相交的阴影部分面积明显增大。对比上面两图,可发现图3(a)中的恒星几何构型优于图3(b),其定位误差范围亦较小。
2.3 三星观测几何构型下的天文定位误差特性分析
同样,分析三星观测条件下的定位性能,根据(6)式可得
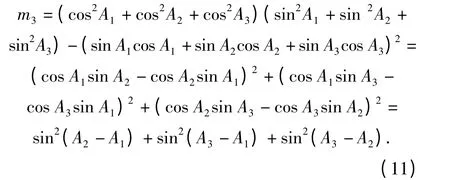
记a=A2-A1,b=A3-A1,则A3-A2=b-a,则

则天文定位均方误差为
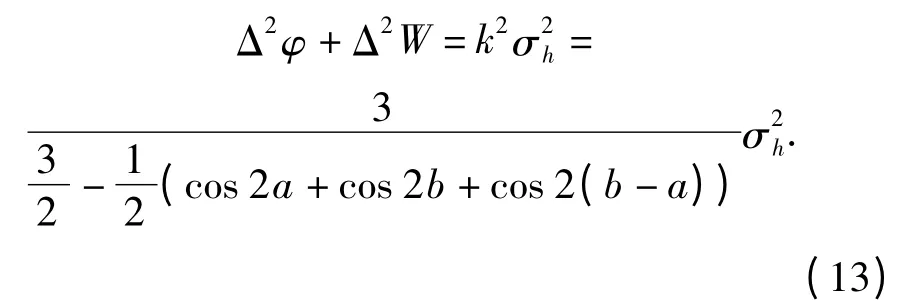
即三星观测条件下天文定位误差特性满足(13)式。经求解,在区间a∈[0,2π],b∈[0,2π]内,m3共有8 个最大值点,具体如表1所示。
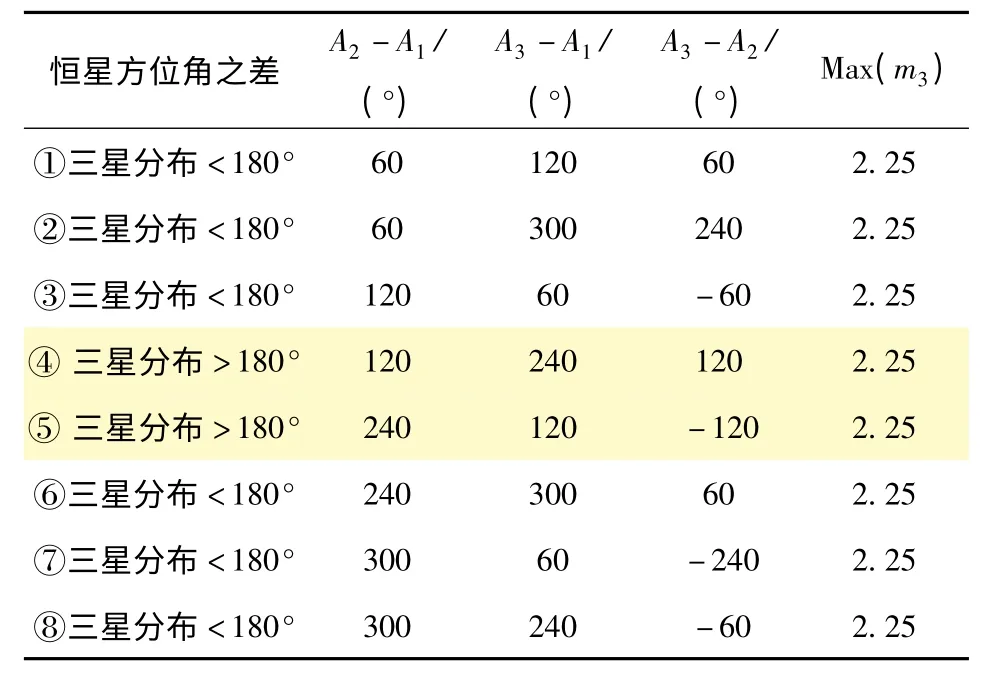
表1 m3 最大值时恒星分布情况Tab.1 Distribution of stars under matrix m3
采用与2.2 节中相同的几何分析方法,来研究三星观测情况下天文定位误差与恒星几何分布中方位角之间的关系。
图4中:图4(a)为表1中的第1 种情况,三星分布<180°;图4(b)为表1中的第5 种情况,三星分布>180°. 对比图4(a)、图4(b)可发现,在这两种情况下,3 颗导航星的等高圆相交的阴影部分形状、大小相同,面积小而集中。图4(c)为3 颗导航星相对于载体分布在同一侧,三星分布<180°;图4(d)为3 颗导航星相对于载体分布在两侧,三星分布>180°. 从图4(c)、图4(d)中可发现,在这两种情况下,3 颗导航星的等高圆相交的阴影部分面积都较大。由此可见,三星定位中,天文定位性能优劣与恒星分布是否大于180°并无直接关系。
3 算法仿真分析
为验证本文所提出的天文定位误差模型的正确性,同时,测试导航星方位角对天文定位性能的影响,本节首先对天文导航双星定位和三星定位分别进行静态仿真,继而结合飞行器动态飞行过程进行天文定位误差特性综合仿真。其中,静态仿真基本条件如表2所示。高度角测量误差设置为均值为0、标准差为10″的高斯白噪声,仿真过程中,恒星之间的方位角之差以0.01°的变化率从0°~360°逐渐增加。
3.1 双星观测下的天文定位误差特性分析
图5和图6给出了双星定位时恒星几何构型中恒星方位角对天文定位性能的影响。从仿真结果看,在区间[0,2π]内,当两颗导航恒星方位角之差在[π/3,2π/3]和[4π/3,5π/3]之间时,天文定位性能较优;当两颗导航恒星方位角之差接近0、π、2π时,天文定位误差明显增大,定位性能显著下降。从图6仿真曲线中可发现,天文定位均方根误差特性与其误差权系数特性一致,可见所建立的双星条件下天文定位误差模型是正确的。

图4 三星观测条件下天文定位误差与恒星方位角之间关系Fig.4 Relationship between positioning error and azimuth under tri-star observing condition

表2 静态仿真基本条件Tab.2 Static simulation parameters

图5 天文定位误差曲线Fig.5 Error curves of celestial positioning
3.2 三星观测下的天文定位误差特性分析
图7给出了三星定位时恒星几何构型中恒星方位角对天文定位性能的影响,图8给出了误差权系数k 和恒星方位角的关系。对比图7和图8可发现,天文定位误差特性与权系数误差特性基本一致,可得所建立的天文定位误差模型是正确的。从图7仿真结果看,当三星几何构型较差时,如其中两颗星方位角之差接近0°、180°、360°时,定位误差权系数明显增大,天文定位性能明显下降。
根据2.3 节分析可知,三星观测下天文定位最优既存在三星分布>180°的几何构型,也存在三星分布<180°的几何构型,为进一步验证恒星方位角分布是否大于180°对天文定位性能是否产生影响,选取以下3 组几何构型进行仿真分析(见表3):恒星几何构型A 为三星分布>180°;恒星几何构型B、C 为三星几何构型中最优的两种,几何构型B 三星分布<180°,几何构型C 三星分布>180°.

图6 天文定位性能曲线Fig.6 Performance curves of celestial positioning
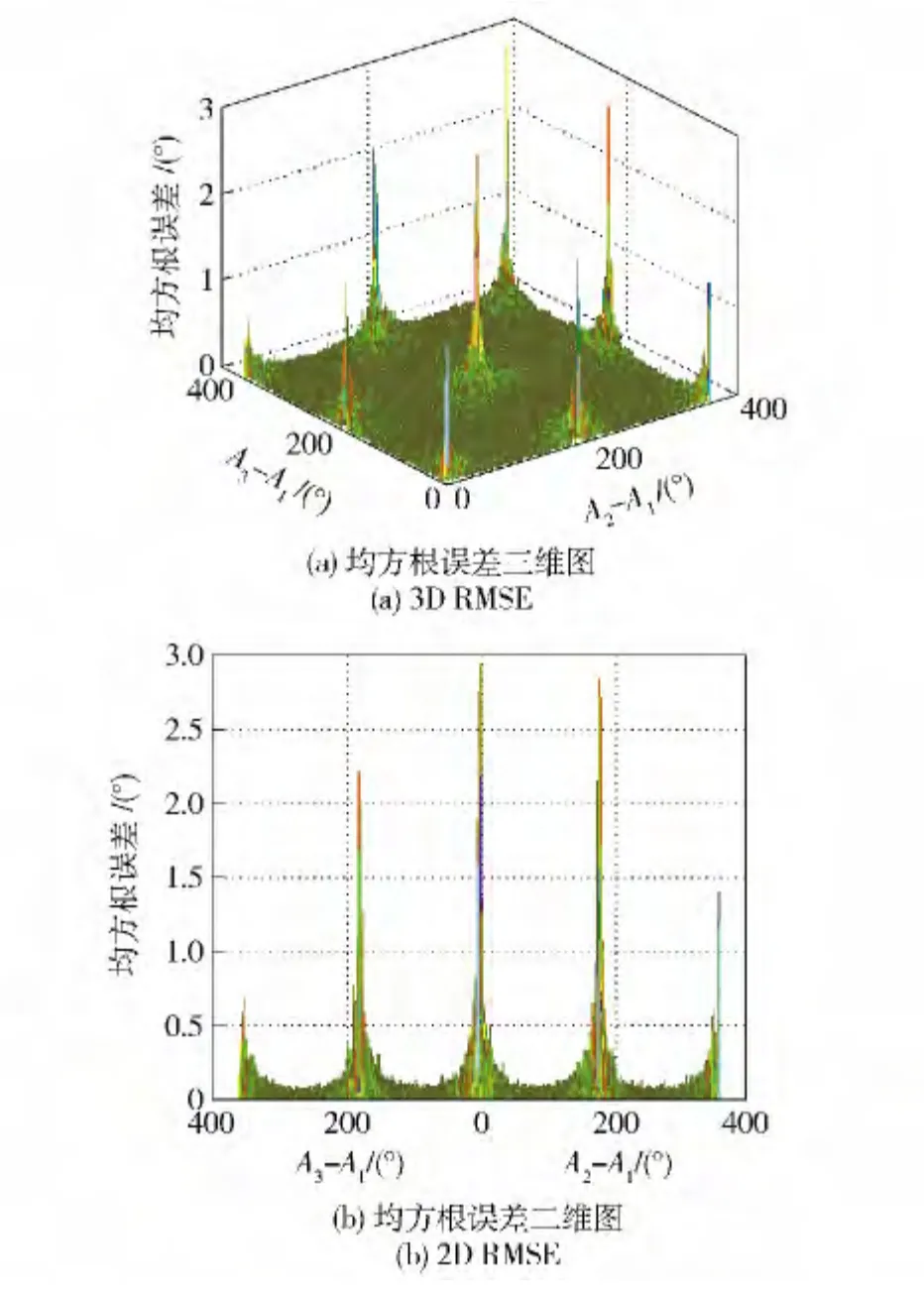
图7 天文定位均方根误差曲线Fig.7 RMSE curves of celestial positioning
如图9所示,对比几何构型A 和几何构型C 下的天文定位性能,可发现A 情况下的天文定位误差大于几何构型C,恒星几何分布>180°并不能保证天文定位性能较优。对比几何构型B、C 下的天文定位性能,两种情况下的天文定位性能基本一致。由此可见,天文三星定位时,在误差权系数相同的情况下,恒星分布是否大于180°对天文定位性能不产生影响。

表3 三星几何构型Tab.3 Distribution of stars
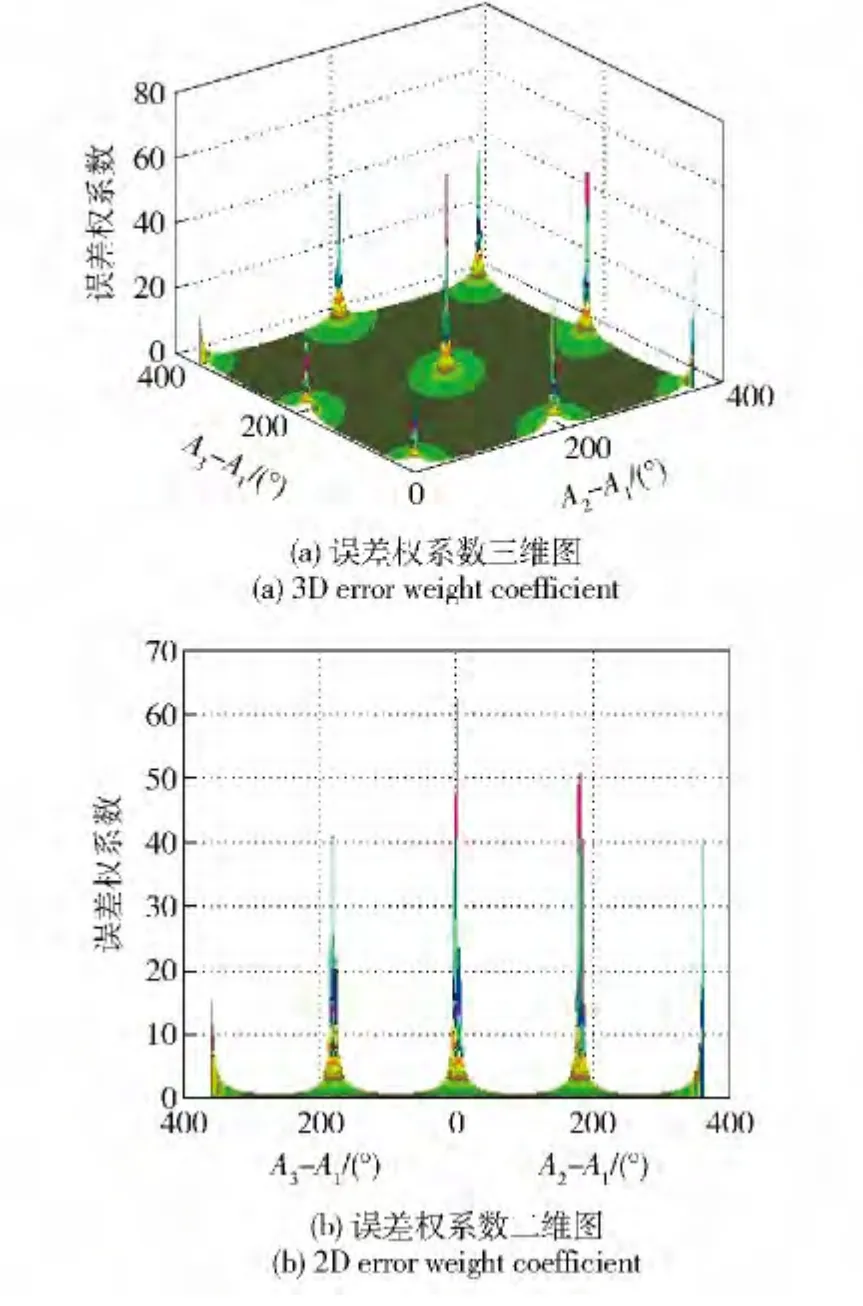
图8 定位误差权系数Fig.8 Error weight curves
3.3 基于恒星几何构型的天文定位误差特性综合仿真分析
为进一步验证所建立的天文定位误差模型的正确性,下面将结合飞行器动态飞行过程,以双星观测为例,采用以下两种方式进行仿真验证:1)考虑恒星几何构型中的方位角影响因素,以恒星方位角之差接近90°为标准进行导航星选择;2)不考虑恒星几何构型分布,将某一时刻飞行器观测到的恒星进行编号(1,…,n),通过随机排序(Matlab 中randperm 函数,基本为等概率原则),随机选取观测到恒星中的两颗作为导航星。
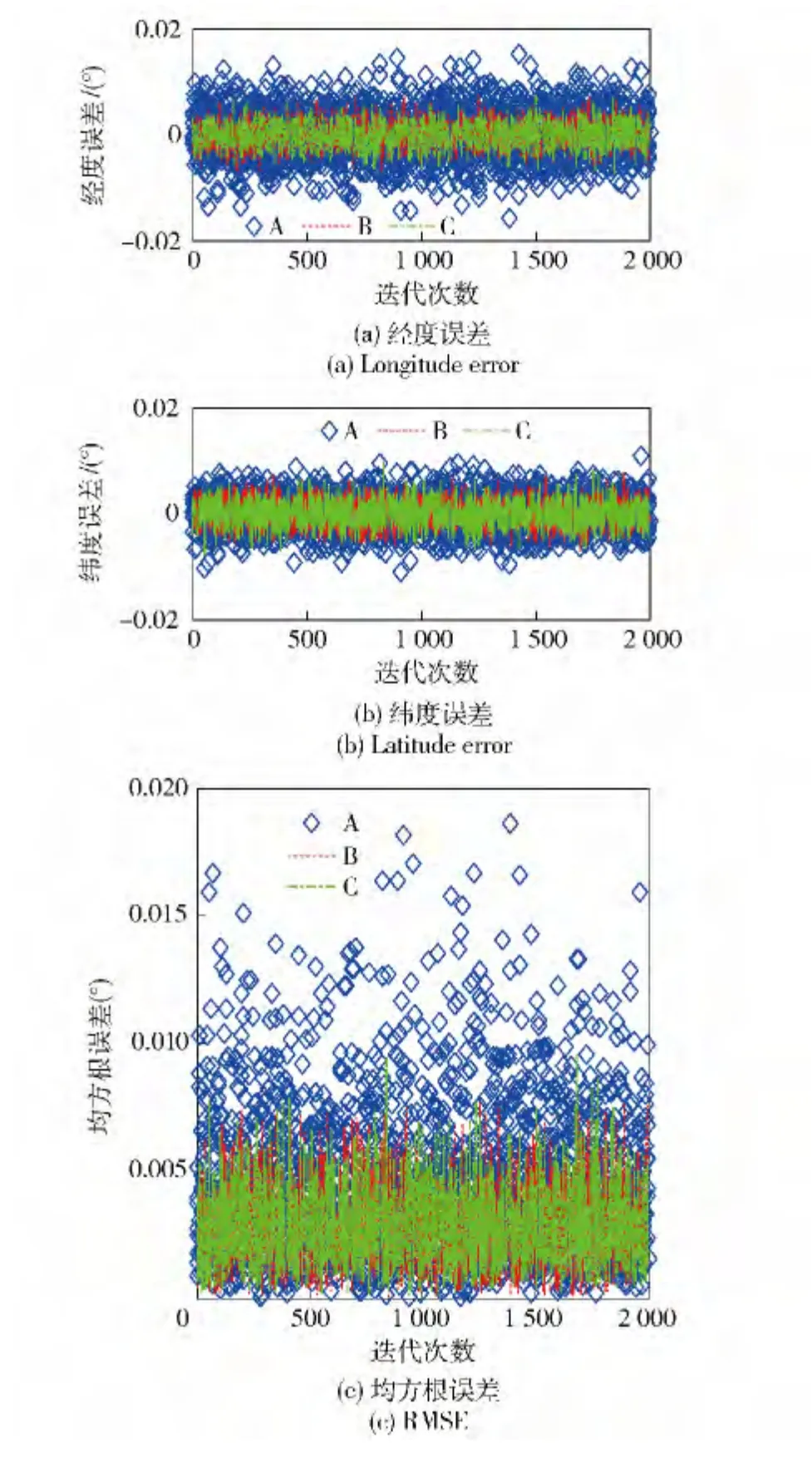
图9 天文定位均方根误差曲线Fig.9 RMSE curves of celestial positioning
考虑到目前天文定位导航主要用在航天飞行器上,为较真实反应天文观测情况,本文结合卫星工具包STK 软件,以飞行高度为500 km 的近地轨道飞行器作为研究对象,构建飞行器飞行场景,分析天文定位误差特性。其中,飞行器参数设定如表4所示,传感器的观测误差如表2所示,为均值为0、标准差为10″的高斯白噪声。飞行器飞行航迹如图10(a)所示,三维飞行场景如图10(b)所示。图10(b)中地球表面的彩点为恒星的星下点,绿色曲线为飞行器飞行轨道,右侧黄色锥型区域表示安装的天文敏感器视场范围,多根黄色直线表示该时刻由天文敏感器观测到的恒星。

表4 飞行器参数设定Tab.4 Aerocraft parameters
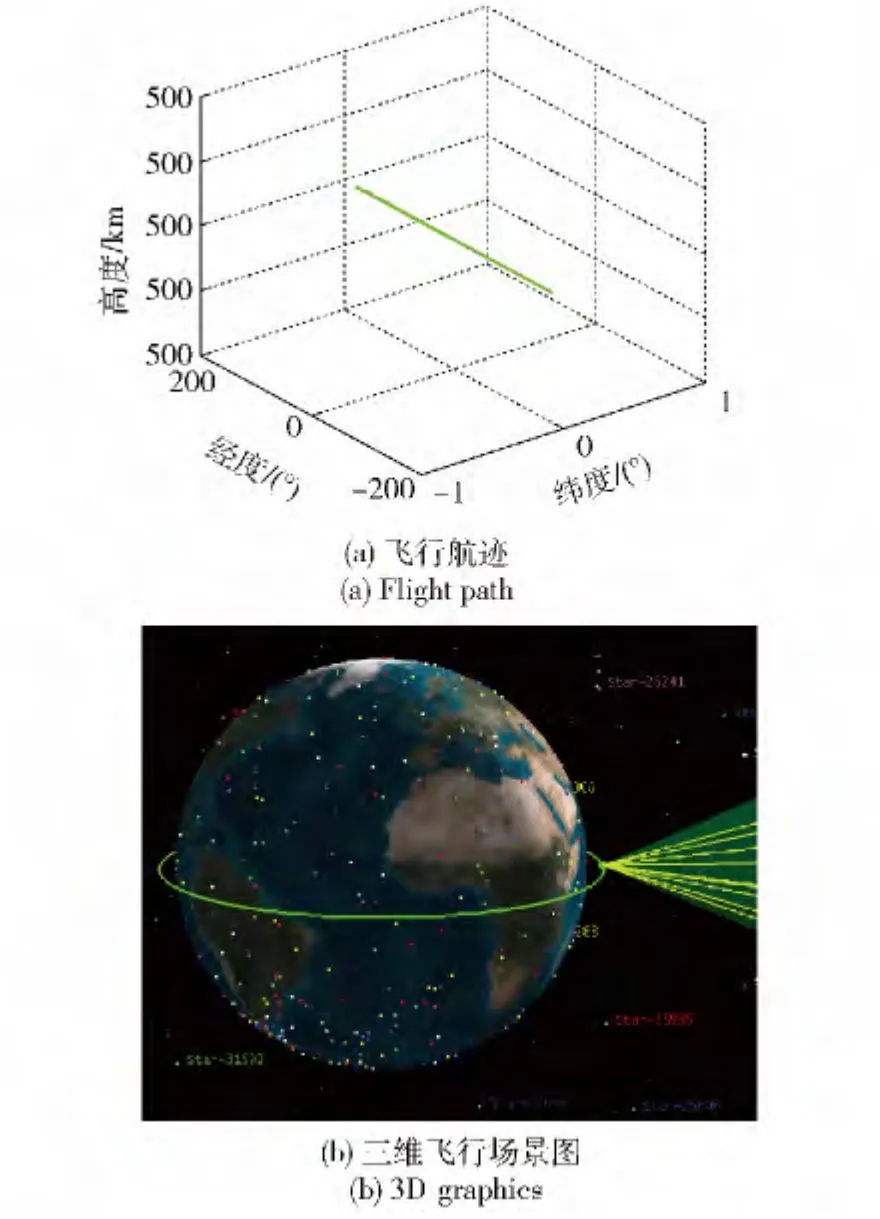
图10 飞行器飞行航迹Fig.10 Aerocraft flight path
在飞行器飞行过程中,天文敏感器观测到的恒星不断变化,因而在数字仿真过程中,以1 min 为步长更新天文敏感器观测的可见星。由于恒星分布并不均匀,因此飞行器不同时刻观测到的恒星数目和恒星分布情况各不相同。图11 给出了飞行器飞行过程中,天文敏感器观测到的可见星数目变化情况。
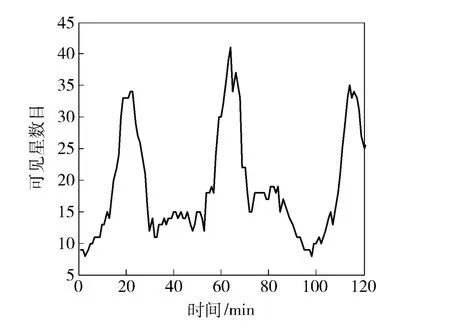
图11 每一时刻观测到的恒星数目Fig.11 Number of navigation stars
结合飞行器飞行航迹,根据上述两种导航星选择方式进行天文定位仿真,分析天文定位误差特性。图12 给出了方位角选星下的天文定位相关曲线,图13 给出了随机选星下的天文定位相关曲线。
从图12(c)、图13(c)可看出,在飞行器动态飞行过程中,不论是以方位角之差进行导航星选择,或是采用随机选星方式,其天文定位均方根误差特性与其对应的误差权系数曲线特性基本一致。由此可见,本文所建立的天文定位误差模型正确,所给出的定位误差权系数k 可有效反映天文导航系统定位性能。
图12(a)、图12(c)中在94 min 处出现一个尖峰,对照图12(b),发现此时两颗导航星之间的方位角之差为171.3°,较接近180°. 图13(a)、图13(c)中在31 min 处出现一个较大尖峰,对照图13(b)发现此时两颗导航星之间的方位角为0.14°,非常接近0°. 从双星观测下的天文定位误差特性分析中可知,当导航星方位角之差接近0°、180°时,天文定位性能较差,因而定位性能曲线中出现尖峰可以得到合理解释。
对比图12(b)、图13(b)可看出,采用方位角选星时导航星方位角之差曲线较接近所设定的90°且曲线平滑,而采用随机选星时导航星方位角之差曲线波动较大且出现较多值接近0°或180°. 对应其天文定位性能曲线图12(c)、图13(c)可发现,方位角选星情况下的天文定位性能明显优于随机选星情况下的天文定位性能。以方位角之差作为导航星选择条件的天文定位误差量级较小且曲线较为平滑。从表5天文定位性能统计数据中亦可看出,采用方位角选星进行天文定位,其经度、纬度误差量级较小,接近于高度角测量误差10″,而采用随机选星方式进行天文定位时,天文定位误差量级较大。由此可见,恒星几何构型中的恒星方位角分布对天文定位性能存在较大影响,选择方位角之差接近90°的恒星作为导航星可有效减小天文定位误差,提高天文定位性能。
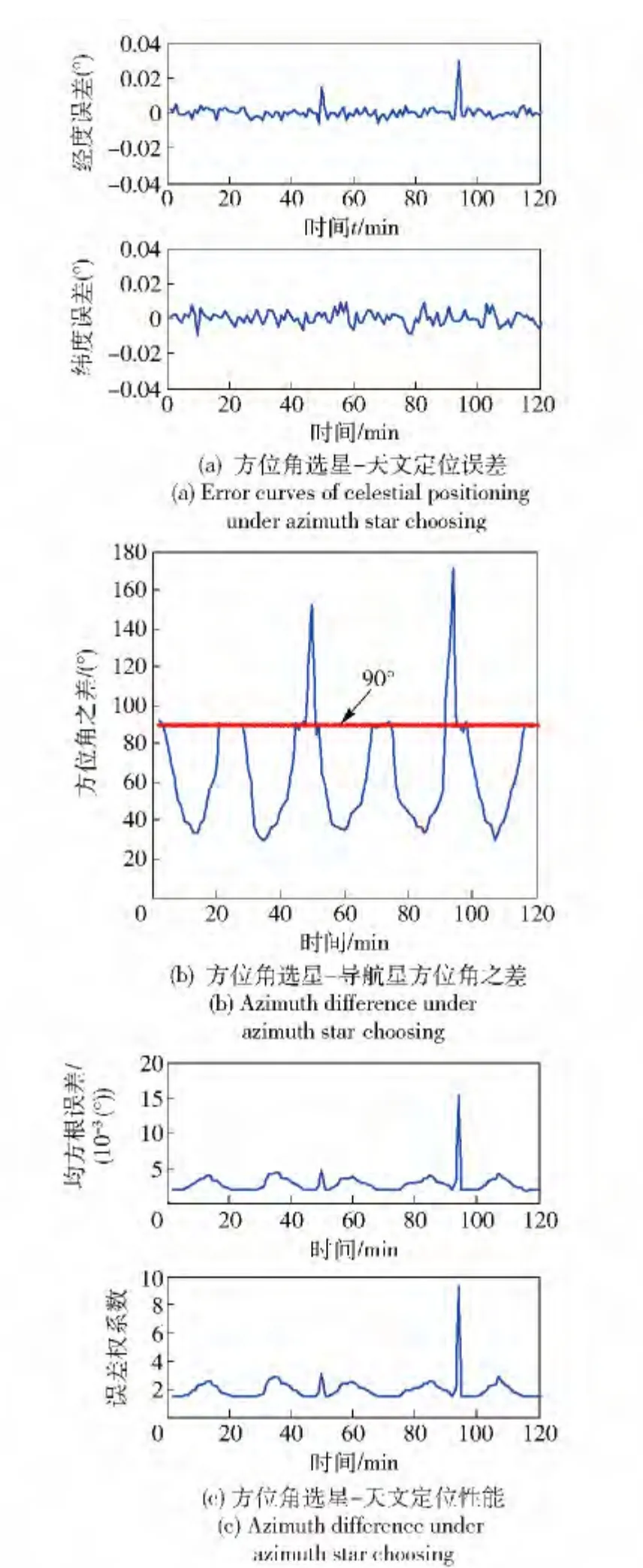
图12 方位角选星下的天文定位曲线Fig.12 Celestial positioning curves under azimuth star choosing

表5 天文定位性能Tab.5 Celestial positioning performance

图13 随机选星下的天文定位曲线Fig13 .Celestial positioning curves under random star choosing
从上述静态仿真和动态仿真结果看,本文所给出的天文定位误差权系数k 可有效反映天文定位过程中的误差特性,由此可证明本文所建立的天文定位误差模型正确有效。
4 结论
天文导航系统作为高自主、高可靠性的导航系统,其重要性不言而喻。如何有效分析天文定位误差、选择合适的导航星是提高其定位性能的前提之一。本文从天文定位基本原理出发,建立了天文定位误差模型,给出了在天文观测精度一定的条件下,天文定位误差权系数k 的表达式。而后以双星定位和三星定位为例,分析了恒星几何构型中恒星方位角对天文定位性能的影响,给出了双星观测和三星观测条件下天文定位性能较优的恒星分布。最后,将所提出的天文定位误差模型分别用于双星定位、三星定位以及飞行器动态飞行过程进行仿真验证。仿真结果表明,所提出的天文定位误差模型正确且可有效用于天文定位性能分析,为天文导航选星提供了参考。
References)
[1]房建成,宁晓琳. 天文导航原理及应用[M]. 北京:北京航空航天大学出版社,2006:3 -9.FANG Jian-cheng. NING Xiao-lin. The theory and application of celestial navigation[M]. Beijing:Beijing University Press,2006:3 -9. (in Chinese)
[2]杨淑洁,杨功流,单友东,等. 空天飞行器SINS/CNS 深组合导航算法[J]. 中国惯性技术学报,2013,21(4):478 -483.YANG Shu-jie,YANG Gong-liu,SHAN You-dong,et al. SINS/CNS tightly integrated navigation algorithm for aerospace vehicles[J]. Journal of Chinese Inertial Technology,2013,21(4):478 -483. (in Chinese)
[3]何炬. 国外天文导航技术发展综述[J]. 舰船科学技术,2006,27(5):91 -96.HE Ju. Survey of overseas celestial navigation technology development[J]. Ship Science and Technology,2006,27(5):91 -96. (in Chinese)
[4]Eduardo dos Santos Pereira. Determining the fixed pattern noise of a CMOS sensor:improving the sensibility of autonomous star trackers [J]. Journal of Aerospace Technology and Management,2013,5(2):217 -222.
[5]Ning X,Fang J. An autonomous celestial navigation method for LEO satellite based on unscented Kalman filter and information fusion[J].Aerospace Science and Technology,2007,11(2):222-228.
[6]Hancock B R,Stirbl R C,Cunningham T J,et al. CMOS active pixel sensor specific performance effects on star tracker/imager position accuracy[C]∥SPIE Proceedings of Optics,Electromechanics and Electronics. San Jose,CA:SPIE,2001:43 -53.
[7]刘垒,张路,郑辛,等. 星敏感器技术研究现状及发展趋势[J]. 红外与激光工程,2007,36(z2):529 -533.LIU Lei,ZHANG Lu,ZHENG Xin,et al. Current situation and development trends of star sensor technology[J]. Infrared and Laser Engineering,2007,36(z2):529 -533. (in Chinese)
[8]廖志波,伏瑞敏,宗肖颖. 星敏感器遮光罩的优化设计[J].中国激光,2010,37(4):987 -990.LIAO Zhi-bo,FU Rui-min,ZONG Xiao-ying. Optimal designing of baffle of star sensor[J]. Chinese Journal of Lasers,2010,37(4):987 -990. (in Chinese)
[9]Wu Z,Yang J,Su D. Experimental study for the effects of stellar spectrums on the location accuracy of a star sensor[C]∥International Symposium on Photo electronic Detection and Imaging 2011.US:International Society for Optics and Photonics,2011.
[10]施闻明,杨晓东. 天文定位中选星系统的建模与仿真[J].系统仿真学报,2007,19(7):1428 -1429.SHI Wen-ming,YANG Xiao-dong. Modeling and simulation on star-choosing in celestial positioning[J]. Journal of System Simulation,2007,19(7):1428 -1429. (in Chinese)
[11]王洪振. 航用天体位置计算及自动选星研究[D]. 大连:大连海事大学,2012.WANG Hong-zhen. The position calculation of marine celestial body and automatic star-choosing in celestial positioning[D].Dalian:Dalian Maritime University,2012. (in Chinese)
[12]于永军,刘建业,熊智,等. 基于多圆迭代和H∞滤波的捷联/天文定位算法研究[J]. 控制与决策,2011,26(5):717 -720.YU Yong-jun,LIU Jian-ye,XIONG Zhi,et al. Research on SINS/CNS integrated navigation algorithm based on multi-circles intersection celestial positioning algorithm and H∞filter[J].Control and Decision,2011,26(5):717 -720. (in Chinese)
[13]熊智,刘建业,郁丰,等. 基于天文角度观测的机载惯性/天文组合滤波算法研究[J]. 宇航学报,2010,31(2):397 -403.XIONG Zhi,LIU Jian-ye,YU Feng,et al. Research of airborne INS/CNS integrated filtering algorithm based on celestial angle observation[J]. Journal of Astronautics,2010,31(2):397 -403,2010. (in Chinese)
[14]程禄,焦传道,黄德鸣. 船舶导航定位系统[M]. 北京:国防工业出版社,1991:103 -110.CHENG Lu,JIAO Chuan-dao,HUANG De-ming. Marine navigation and positioning systems[M]. Beijing:National Defense Industry Press,1991:103 -110. (in Chinese)

