基于神经网络和遗传算法的火炮结构动力学优化

梁传建，杨国来，王晓锋

(南京理工大学 机械工程学院，江苏 南京210094)

0 引言

射击精度是考核火炮性能的主要技术指标，而炮口扰动对射击精度具有重要的影响。研究表明，炮口扰动与后坐质量偏心、炮口制退器质量、制退机布置、部件间的间隙等火炮总体结构参数是紧密相关的［1-4］。为了减小炮口扰动，科研人员做了大量的工作。贾长治等［5］建立了火炮多体系统动力学模型，对影响炮口扰动的参数进行了灵敏度分析，并结合序列二次规划算法与虚拟样机对火炮进行了动力学优化，优化后火炮的动态特性得到了显著的改善;文献［4，6］则结合多体动力学及遗传算法对火炮总体参数进行了动力学优化，优化后炮口扰动明显减小。崔凯波等［7］利用多体系统动力学计算炮口扰动，通过均匀试验设计和神经网络建立炮口扰动和结构参数之间的非线性映射关系，建立了优化目标函数，但未开展优化研究。上述文献均是以多体动力学理论为基础，这主要是考虑到多体动力学模型所需计算时间短，具有较高的计算效率。但火炮多体动力学模型由于难以充分考虑各部件的柔性效应，制约了计算精度和优化水平的提高，需要开展进一步的改进研究。

有限元法考虑了火炮构件的弹性变形，能够反映火炮的模态特性、应力、应变的分布情况及各种响应，并能考虑接触碰撞等非线性因素，具有相对较高的计算精度，在火炮动力学研究中得到广泛应用［8-10］。然而，由于基于有限元的结构动力学方程数目庞大，所需计算时间长，而且结构动力学优化中对目标函数的求解常常需要成千上万遍的计算，从而导致以有限元为基础的结构动力学优化难以实现，成为制约复杂结构动力学优化研究的技术瓶颈。为了解决上述问题，研究人员提出了采用神经网络响应面近似模型代替有限元模型，以运用到机械结构的优化过程中，这大大提高了优化效率，工程中大量的成功算例证明了该方法的有效性和可行性［11-13］，但目前有关以非线性有限元模型为基础进行火炮总体结构动力学优化的文献报道较少。本文以某大口径火炮上装部分为研究对象，建立基于非线性有限元的结构动力学模型，结合最优拉丁超立方设计和数值计算获得了不同结构参数下的炮口振动响应数据。以该数据为神经网络输出，建立反向传播(BP)神经网络来模拟火炮总体结构参数与炮口扰动之间的非线性映射关系。以神经网络近似模型代替有限元模型，结合遗传算法实现了火炮总体结构动力学优化，利用有限元软件对优化后的火炮总体结构进行了非线性动力学数值计算，通过对比分析说明所提方法的可行性。

1 火炮结构动力学建模

1.1 非线性有限元建模

本文所研究的火炮是上装部分直接安装在刚性很大的台架上的试验样炮，由于台架刚性很大，且弹丸膛内运动时间仅为十几毫秒，台架对炮口扰动的影响可以忽略不计，故仅建立火炮上装部分的有限元模型。对摇架护筒、复进机筒、制退机筒、上架两侧的薄钢板和加强筋等主要采用减缩积分壳单元进行网格划分;摇架本体、炮口制退器、身管、炮尾炮闩、衬套、座圈、高低机齿轮齿弧等结构考虑到造型复杂、存在接触/碰撞关系等特性，主要采用六面体减缩积分单元进行网格划分;平衡机以弹簧单元进行模拟;对一些非结构件如瞄具、液量调节器等通过集中质量单元来模拟;为了便于输出炮口处的角位移和角速度，在炮口中心点处设置参考点，并用耦合约束连接该参考点与炮口处的单元节点。

火炮各部件间的连接非常复杂，具有高度的非线性，对计算结果有着重要的影响，必须对这些连接关系进行妥善处理。对摇架耳轴与上架耳轴座之间的连接用自由度耦合来模拟，只释放绕耳轴轴线方向的旋转自由度，同样的方法可用来模拟高低机齿轮轴与上架轴承座之间的连接;在高低机齿轮齿弧之间可能发生接触的表面区域定义面对面的接触对来模拟齿轮与齿弧间的接触碰撞关系，同样的方法可用来模拟身管与衬套之间以及定向栓与定向槽之间的接触碰撞关系。

所建火炮上装部分有限元模型共有736 826 个单元、802 112 个节点，如图1所示。建立坐标系方向如下:与身管轴线重合的坐标轴定为x 轴，其正方向由炮尾指向炮口，与身管轴线垂直且指向上方的方向为y 轴正方向，z 轴由右手定则确定。

1.2 载荷与边界条件

火炮发射过程中受到的主动力有重力和火药气体作用力，而所受到的内力主要有复进机力和制退机力。在本文的研究中，重力载荷作为常力直接加载在模型中，火药气体作用力则通过在炮尾上施加随时间变化的等效压力来模拟，而复进机力则通过在复进机与炮尾和摇架的连接点上施加一对共线且反向的随时间变化的集中力来模拟，制退机力的模拟与复进机力的模拟相似。等效压力、复进机力和制退机力随时间变化曲线分别如图2、图3所示。在座圈底面施加全约束边界条件。

图1 某火炮上装有限元模型Fig.1 Finite element model of a gun top section

图2 等效压力Fig.2 Equivalent pressure

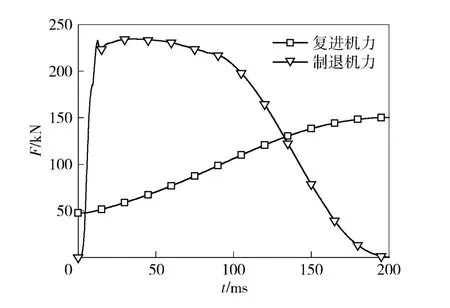
图3 复进机力和制退机力Fig.3 Recuperator force and recoil force

2 神经网络建模

火炮总体结构参数与炮口扰动之间是一种复杂的非线性映射关系，并没有确定的函数关系。而人工神经网络具有非常强的非线性映射能力，它不需要任何先验公式就可通过学习(或训练)自动总结出数据间的函数关系，是一种非常有效的建模手段。理论已经证明，一个3 层BP 神经网络能够充分逼近任意复杂的非线性函数，即可以实现任意的n 维到m 维的映射。综合考虑研究对象与BP 神经网络结构的特点，采用BP 神经网络来构建近似模型。

2.1 优化设计变量选择

为有效降低火炮炮口扰动，应选择对炮口扰动影响较大的总体结构参数作为优化结构参数。根据以往经验，选取后坐部分质量的垂向偏心距ey和横向偏心距ez、炮口制退器质量mz、前衬瓦轴向偏移量lx、制退机布局角θ 作为优化设计变量。其中:lx为前衬瓦相对于初始位置沿x 轴方向的位移，θ 为过制退机力作用点和身管轴线的平面与Oxy 平面的夹角。各结构参数的初值和取值范围如表1所示。

表1 设计变量初值和取值范围Tab.1 Initial values and value range of design variables

2.2 试验设计

试验设计是以概率统计为理论基础，研究多因子与响应变量关系的一种科学方法。拉丁超立方设计是一种基于随机抽样的试验设计方法，具有有效的空间填充能力和超强的非线性响应拟合能力等特点。最优拉丁超立方设计通过外加一个准则大大改进了拉丁超立方设计的均匀性，使因子和响应的拟合更加精确、真实，特别适合于多因素多水平的试验和系统模型完全未知的情况。

建立神经网络模型需要一系列训练样本，合理的训练样本数量及分布能使神经网络模型确切地表达结构的映射关系。火炮总体结构较为复杂，其动态响应具有很强的非线性，训练样本数量必须足够充分。鉴于此，本文以最优拉丁超立方设计来安排试验，在各设计变量的取值区间内均匀地取81 个水平，从而构成样本总数为81 的输入样本。根据样本对第1 节建立的火炮动力学模型做相应修改并采用隐式直接积分算法进行动力学分析，从而获得高低射角和方向射角均为0°时的火炮动态响应。本文的优化设计是以降低炮口扰动为主要目的，而弹丸出炮口时刻的炮口角位移和角速度是衡量炮口初始扰动的主要指标，故提取弹丸出炮口时的炮口回转角位移θy、高低角位移θz、回转角速度ωy和高低角速度ωz作为炮口扰动的输出样本，至此获得了由输入和输出样本共同建立的试验样本库，以供人工神经网络进行学习和训练。

2.3 神经网络模型的构建

研究表明，在BP 神经网络中引入贝叶斯正则化算法有利于优化网络结构、提高多变量大样本输入情况下网络的泛化能力和逼近精度［14］。通过大量的实际训练和检测比较发现:采用多输入、单输出及单隐含层的3 层网络结构建立的神经网络模型，其训练、检测精度均远远优于多个输出的情况。因此，本文利用Matlab 神经网络工具箱构建了4 个BP 神经网络模型来分别模拟设计变量与弹丸出炮口时的炮口回转角位移θy、高低角位移θz、回转角速度ωy和高低角速度ωz之间的非线性映射关系，并选用trainbr 训练函数来实现贝叶斯正则化算法。各BP 神经网络均由输入层、隐层和输出层3 层神经元组成。输入层节点数均为5;隐层节点数通过反复试算分别加以确定，其传递函数均采用tansig 函数;输出层节点数均为1，其传递函数均采用purelin 函数。BP 网络的拓扑结构如图4所示。

图4 BP 神经网络拓扑结构示意图Fig.4 Topology of the BP neural network

以2.2 节获得的81 组试验样本作为训练集，利用Matlab 神经网络工具箱对构建的BP 神经网络进行训练，从而获得经过训练的BP 神经网络。为了获得较好的训练效果，应在训练前对样本数据进行归一化处理，使所有数据在［0.1，0.9］之间。

2.4 神经网络模型质量检验

训练后的神经网络模型还应检验其泛化能力和预测精度。利用最优拉丁超立方设计在设计变量的取值范围内均匀而随机地选取15 组数据，并进行相应的动力学分析来获得炮口响应量，从而可得到15 组检测样本。神经网络模型对检测样本的数据拟合度可用复相关系数R2检验。R2的表达式分别为

表2 检验结果Tab.2 Results of inspection

由表2可知，神经网络预测的复相关系数均接近1，表明构建的BP 网络具有较高的预测精度和良好的泛化能力。

3 基于遗传算法的火炮结构动力学优化

3.1 目标函数构建

在以降低火炮炮口扰动为目标对火炮总体结构参数进行优化时，为了使表征炮口初始扰动的优化目标函数同时包含弹丸出炮口时的炮口角位移和角速度的影响，采用线性加权将多目标优化问题转化为单目标优化问题，由于角位移和角速度的量纲不同，还应对目标函数进行归一化处理。所建的优化目标函数为

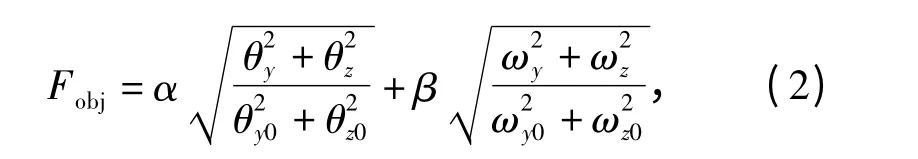
式中:θy0、θz0、ωy0、ωz0分别为设计变量取初始值时弹丸出炮口瞬间的炮口回转角位移、高低角位移、回转角速度、高低角速度;α、β 为加权系数，其值一般由经验获取，在此分别取为0.3、0.7.

结合(2)式和第2 节建立的BP 神经网络模型即可建立起设计变量与目标函数之间的函数关系。

3.2 基于遗传算法的优化和结果分析

基于神经网络模型建立的函数关系是通过神经元间的连接权值与阈值来实现的，难以用传统优化方法对此类问题寻优。而遗传算法是一种不需要具体函数形式的非数值进化优化算法，可以寻得全局最优解，适合于离散变量的优化问题，因此采用遗传算法进行火炮结构动力学优化。

以目标函数Fobj最小化为目标，在设计变量的取值范围内采用遗传算法进行优化计算，经圆整后的结构参数优化结果如表3所示。基于表3的优化参数对火炮进行有限元分析，并将结果(弹丸出炮口时刻的炮口响应量)与神经网络计算结果进行对比分析，如表4所示。优化前后炮口角位移和角速度随时间变化曲线如图5、图6所示。

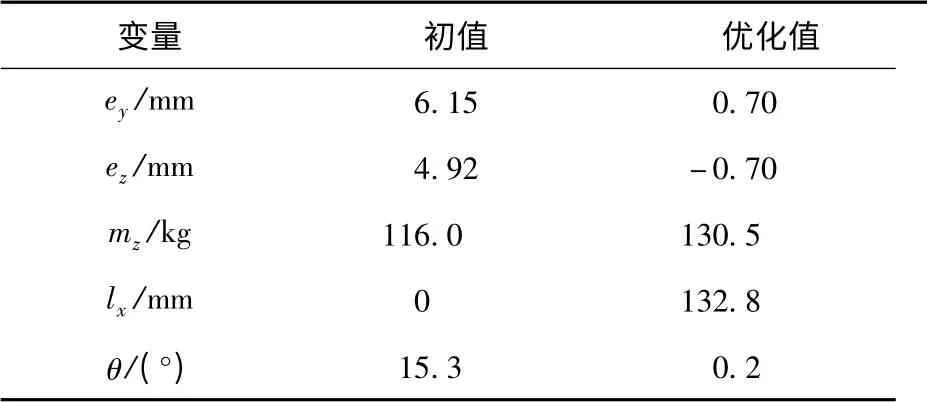
表3 结构参数优化结果Tab.3 Optimized results of structural parameters

表4 优化结果对比Tab.4 Comparative analysis of optimized results

图5 优化前后炮口角位移变化曲线Fig.5 Curves of muzzle angular displacement before and after optimization

由表4可以看出，采用神经网络和遗传算法优化后目标函数Fobj减小了57.16%，弹丸出炮口时刻的角位移和角速度的绝对值均显著减小，达到了炮口扰动优化的目的。此外，由表4还可以看出，神经网络计算结果与有限元计算结果吻合得非常好，这进一步说明了建立的神经网络模型具有很好的预测性和精度，同时也说明了基于神经网络和遗传算法的优化结果具有较高的可信度。由图5和图6可知，优化后的炮口扰动在整个弹丸膛内运动时期(对应前13 ms)比优化前明显减小，这表明优化效果非常理想。

图6 优化前后炮口角速移变化曲线Fig.6 Curves of muzzle angular velocity before and after optimization

4 结论

以某大口径火炮样机上装部分为研究对象，基于非线性有限元理论，建立了火炮发射动力学模型。针对炮口扰动优化存在的技术难点，提出了采用有限元法、试验设计、神经网络和遗传算法相结合的火炮动力优化新方法。研究结果表明:

1)基于最优拉丁超立方设计和贝叶斯正则化算法建立的BP 神经网络近似模型具有较高的预测精度和良好的泛化能力，能够很好地建立火炮结构参数与炮口扰动之间非线性映射关系，可以有效地解决目标函数无法用设计变量显式表达的问题。

2)神经网络和遗传算法相结合可以有效地求解目标函数来获得优化结果，神经网络计算结果与有限元计算结果吻合得非常好，优化后炮口的角位移和角速度均显著减小，可见该方法行之有效。

本文对基于神经网络的火炮总体结构动力学优化进行了初步的研究，设计变量的数目相对较少，目标函数构建相对比较简单，后续研究将进一步开展目标函数的合理性、考虑工程设计需求的设计变量选取等方面的研究。

References)

［1］Cox P A，Hokanson J C. The influence of tube support condition on muzzle motions，ADA119726［R］. New York:Army Armament Research，Development and Engineering Center，1982.

［2］蔡文勇，陈运生，杨国来. 车载火炮炮口扰动影响因素分析［J］.南京理工大学学报，2005，29(6):658 -661.CAI Wen-yong，CHEN Yun-sheng，YANG Guo-lai. Impacts of structural parameters on muzzle disturbance for a vehicle mounted howitzer［J］. Journal of Nanjing University of Science and Technology，2005，29(6):658 -661. (in Chinese)

［3］梁传建，杨国来，王晓锋，等.反后坐装置结构布置对炮口振动影响的研究［J］.兵工学报，2013，34(10):1209 -1214.LIANG Chuan-jian，YANG Guo-lai，WANG Xiao-feng，et al.Study on influence of structural arrangement of recoil mechanism on muzzle vibration of gun［J］. Acta Armamentarii，2013，34(10):1209 -1214. (in Chinese)

［4］陈世业.自行火炮弹炮多体发射系统动力学仿真研究［D］.南京:南京理工大学，2013.CHEN Shi-ye. Dynamics simulation for the projectile-barrel multibody launching system of the self-propelled artillery［D］.Nanjing:Nanjing University of Science and Technology，2013. (in Chinese)

［5］贾长治，郑坚.结构设计参数对火炮炮口振动影响的仿真及基于SQP 方法的优化［J］.机械工程学报，2006，42(9):130-134.JIA Chang-zhi，ZHENG Jian. Effect simulation of design parameters on muzzle vibration of guns and optimization with SQP method［J］. Journal of Mechanical Engineering，2006，42(9):130 -134. (in Chinese)

［6］蔡文勇，马福球，杨国来. 基于遗传算法的火炮总体参数动力学优化［J］.兵工学报，2006，27(6):974 -977.CAI Wen-yong，MA Fu-qiu，YANG Guo-lai. Dynamic overall parameter optimization of howitzer with genetic algorithm［J］. Acta Armamentarii，2006，27(6):974 -977. (in Chinese)

［7］崔凯波，秦俊奇，狄长春，等.基于均匀设计与RBF 网络的火炮优化目标函数构建方法研究［J］. 机械设计，2013，30(2):45 -48.CUI Kai-bo，QIN Jun-qi，DI Chang-chun，et al. Research on establishment measures of artillery objective function by uniform design method and RBF network［J］. Journal of Machine Design，2013，30(2):45 -48. (in Chinese)

［8］王虎，顾克秋.牵引火炮非线性有限元隐式动力学分析［J］.南京理工大学学报，2006，30(4):462 -466.WANG Hu，GU Ke-qiu. Implicit dynamics analysis of nonlinear finite element for towed howitzer［J］. Journal of Nanjing University of Science and Technology，2006，30(4):462 -466. (in Chinese)

［9］葛建立，杨国来，陈运生，等. 基于弹塑性接触/碰撞模型的弹炮耦合问题研究［J］.弹道学报，2008，20(3):103 -106.GE Jian-li，YANG Guo-lai，CHEN Yun-sheng，et al. A study on projectile-barrel coupling problem based on elasto-plastic contact/impact model［J］. Journal of Ballistics，2008，20(3):103 -106. (in Chinese)

［10］张永存，吴雪云，刘书田.典型火炮结构振动分析与前支架设计改进［J］.工程力学，2013，30(6):308 -312.ZHANG Yong-cun，WU Xue-yun，LIU Shu-tian. Vibration analysis of typical artillery and improvement of front bracket［J］. Engineering Mechanics，2013，30(6):308 -312. (in Chinese)

［11］孟广伟，沙丽荣，李锋，等. 基于神经网络的结构疲劳可靠性优化设计［J］.兵工学报，2010，31(6):765 -769.MENG Guang-wei，SHA Li-rong，LI Feng，et al. Design optimization for structural fatigue reliability based on artificial neural network［J］. Acta Armamentarii，2010，31(6):765 -769. (in Chinese)

［12］张本军，王瑞林，李永建，等.基于BP 网络和遗传算法的枪架结构优化［J］.振动与冲击，2011，30(1):142 -144.ZHANG Ben-jun，WANG Rui-lin，LI Yong-jian，et al.Structural optimization for a machine-gun mount based on BP neural network and genetic algorithm［J］. Journal of Vibration and Shock，2011，30(1):142 -144. (in Chinese)

［13］谢延敏，王新宝，王智，等. 基于灰色理论和GA-BP 的拉延筋参数反求［J］.机械工程学报，2013，49(4):44 -50.XIE Yan-min，WANG Xin-bao，WANG Zhi，et al. Parameter inverse problem for drawbeads based on the gray theory and GABP［J］.Journal of Mechanical Engineering，2013，49(4):44 -50. (in Chinese)

［14］MacKay D J C. A practical Bayesian framework for back propagation networks［J］. Neural Computation，1992，4(3):448 -472.