超宽带无线电引信回波信号建模与仿真

沈磊，黄忠华

(北京理工大学 机电学院，北京100081)

0 引言

超宽带无线电引信具有定距精度高、抗干扰能力强的特点，具有广泛的应用前景。由于超宽带信号辐射、散射的特殊性以及引信近场工作的特点，引信天线接收信号与发射信号有很大差别。超宽带无线带引信对地回波信号的最高频率为数吉赫兹，且淹没在噪声中，很难得到回波信号的实测波形，给引信接收机和信号处理电路设计带来了很大困难，因此迫切需要对超宽带无线电引信回波信号进行理论研究，为引信接收机和信号处理电路设计提供理论指导［1-3］。

目前，国内对于超宽带无线电引信回波信号的研究还不是很深入，总体来说，在超宽带无线电引信回波信号建模的研究上遇到的问题有:引信目标为地面时，引信天线波束照射范围内各散射体距离的不同将导致地面散射信号返回到引信接收天线的时间不一致，从而造成地面回波信号的展宽效应。由于超宽带无线电引信辐射信号脉冲宽度很窄，这种展宽效应将更加明显，这就是超宽带信号的多径效应。多径效应将影响超宽带无线电引信回波信号的建模;地面是典型的分布反射目标，是由大量散射体、反射体和吸收体组合而成的，当电磁波入射到地面时，会发生电磁场的反射、散射以及目标介质的吸收和极化等现象，主要表现为电磁波的镜面反射和漫反射两种情况。因此，地面的散射特性给超宽带无线电引信回波信号的建模带来了困难［4-5］。

针对上述问题，本文针对平坦地面建立超宽带无线电引信与地面关系图，并推导出了超宽带无线电引信回波信号表达式，得到了超宽带无线电引信回波信号波形。通过与实测波形的比较，验证了建模的正确性。

1 地面散射特性

当地面起伏度h 和入射角余角θ'满足(1)式时，可将目标看作光滑表面，电磁波产生镜面反射，服从几何光学的反射定理，否则需看作粗糙表面［6］。

式中:c 为光速;f 为信号频率。(1)式即为瑞利判据。由此可见，当辐射信号照射到目标表面时，目标回波信号表现为镜面反射状态还是漫反射状态，主要取决于目标表面起伏度、电磁波的入射角及信号频率。入射信号频率越高，所能满足镜面反射条件的目标起伏度就越小，要求目标表面越光滑。

对于不满足(1)式的粗糙地面，其反射可看为镜面反射分量和漫反射分量之和，这两种分量也被称为相干分量和非相干分量［6-7］。垂直入射时，粗糙表面将总入射功率镜面反射出去的比例［8］为

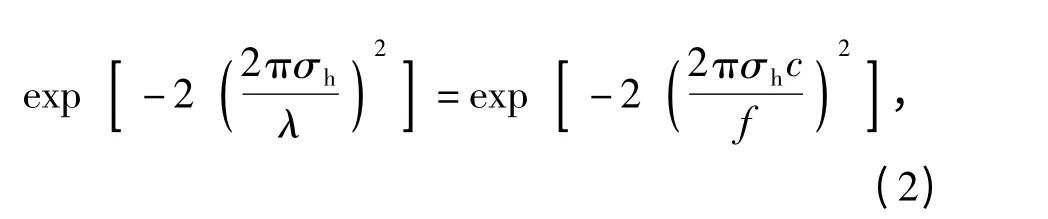
式中:σh为粗糙表面均方高度;λ 为波长。如图1所示粗糙地面镜面反射比例。

图1 粗糙地面镜面反射比例Fig.1 The proportion of rough ground specular reflection

由图1可见，对波长为固定值的入射波，随着地面粗糙程度的增加，镜面反射分量越来越小。σh=0.10λ 时，镜面反射比例为37.73%;σh=0.20λ 时，镜面反射比例为2.03%. 超宽带无线电引信对一般地面而言，漫反射能量占总反射能量的绝大部分，可将超宽带无线电引信地面反射近似认为是完全漫反射，如图2所示［9-10］。

图2 漫反射示意图Fig.2 Diffuse reflection

2 平坦地面回波信号建模

假设地面是由同类介质构成的均匀起伏的平坦表面，该粗糙表面由多个均匀放置的独立散射体构成，且每个散射体的尺寸相差不大，在此模型基础上，可推导对地超宽带无线电引信回波信号。

超宽带无线电引信地面回波信号可看作是由大量均匀分布的独立散射体产生的，则地面的冲激响应可利用(3)式表示:

式中:h(t)为目标的冲激响应;ai为回波信号幅度衰减;τi为回波延迟

由于重点讨论的为单个脉冲的回波信号时域波形，故假设天线激励信号为单个高斯2 阶导数w(t)，即可得到超宽带无线电引信回波信号表达式为

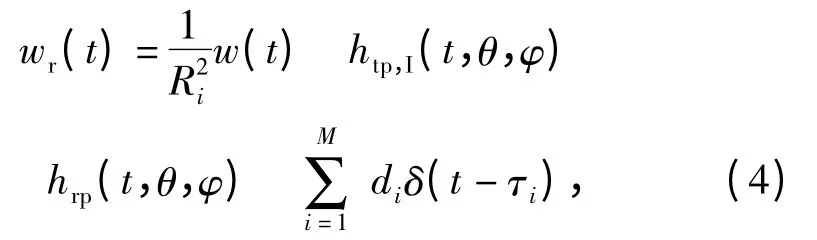
式中:w(t)为高斯2 阶导数;htp，I(t，θ，φ)为发射天线冲激响应;hrp(t，θ，φ)为接收天线冲激响应;di=

记

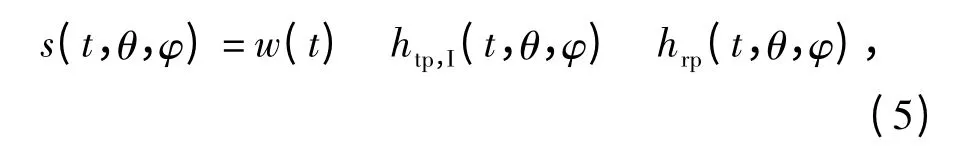
则(4)式可写为

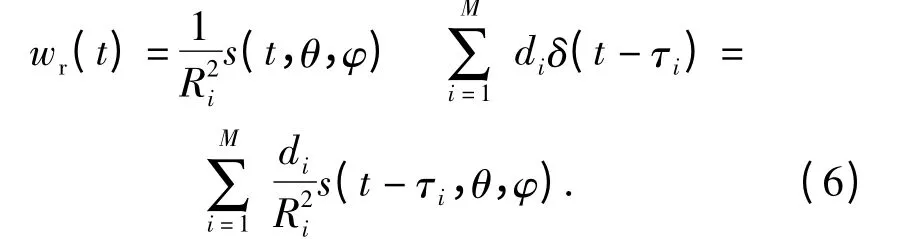
假设各个散射体的冲激响应幅度衰减系数相等，记为d，则单位面积幅度衰减系数为

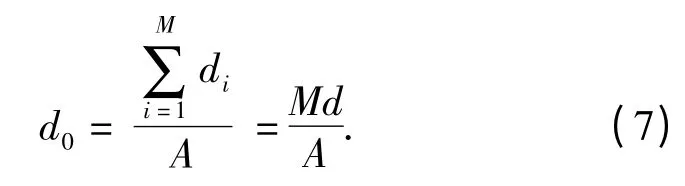
由于引信照射区域内散射体的个数M 与照射区域的面积A 呈正比，令k 为常数，则

在对地窄带雷达方程中，采用了平均散射截面积即总的散射截面积与面积A 的比值的概念为度量面目标的散射特性，定义为

在窄带雷达方程中，目标雷达散射截面积是一个非常重要的量，它是目标的一种假想面积，是在给定方向上目标返回或散射功率的一种度量［11］，定义为

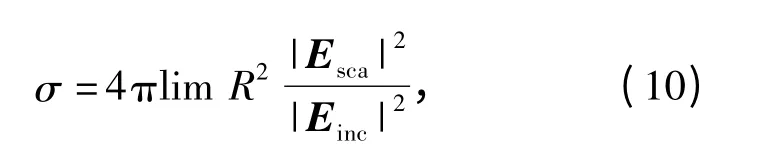
式中:Esca为散射电场;Einc为入射电场;R 为引信到面积元dA 的距离。

在引入目标冲激响应函数的概念之后，目标的散射场可写为入射场与目标冲激响应函数的卷积，数学表达式为

对(11)式进行傅里叶变换可得

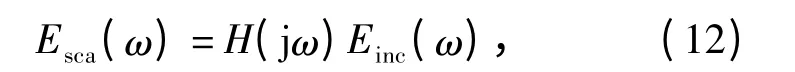
将(12)式带入(10)式可得

由(13)式可得单个散射体的雷达散射截面积和目标冲激响应幅度衰减系数之间的关系为

由(8)式、(9)式和(15)式可得

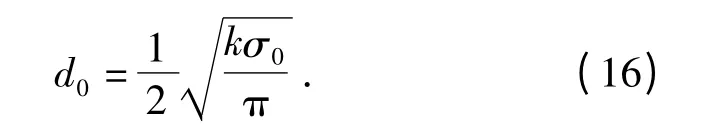
引信天线波束与地面的几何关系如图3所示。Oxy 表示平坦地面，D 为引信位置，弹纵轴与Oxy 平面的交点为E，与z 轴之间的夹角为ξ，弹纵轴在Oxy 平面的投影与x 轴之间的夹角为α，天线波束入射方向与引信到面积元dA 的连线DF 之间的夹角为ϑ，DF 与z 轴之间的夹角为θ，面积元dA 在Oxy 平面上与x 轴之间的夹角为φ，H 为引信到地面的高度。

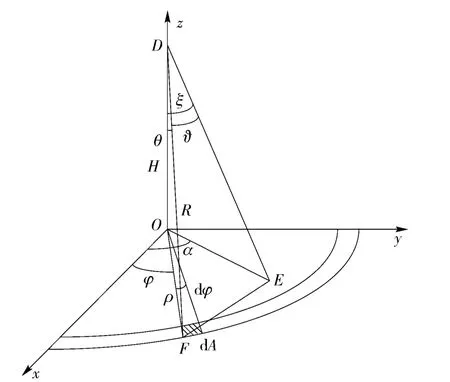
图3 引信天线与地面几何关系Fig.3 Geometrical relationship of fuze antenna and ground

单位面积幅度衰减系数d0为θ 的函数，记为a0(θ)，面积元dA 的幅度衰减系数为a0(θ)dA，可得来自面积元dA 的回波信号为

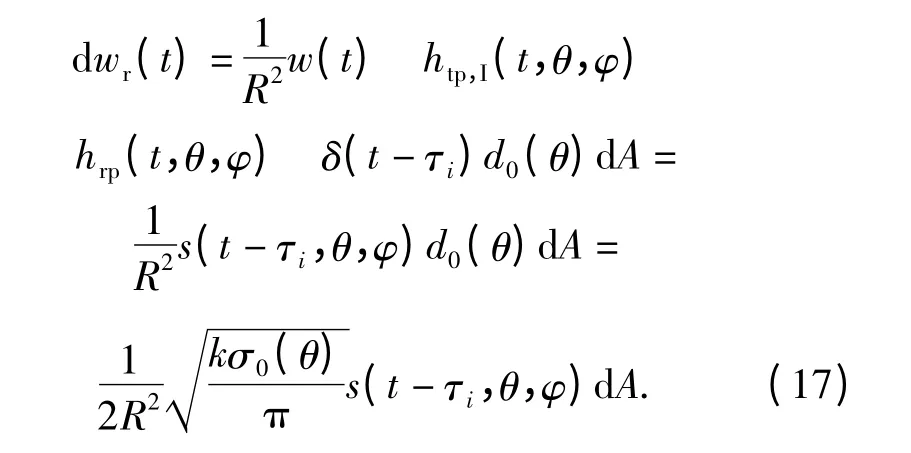
为了得到回波信号表达式，对(17)式进行积分可得

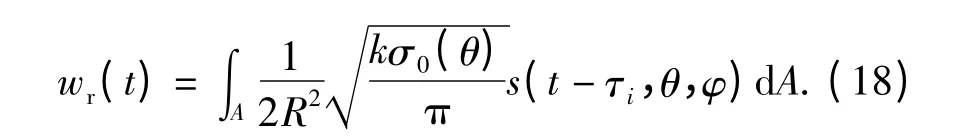
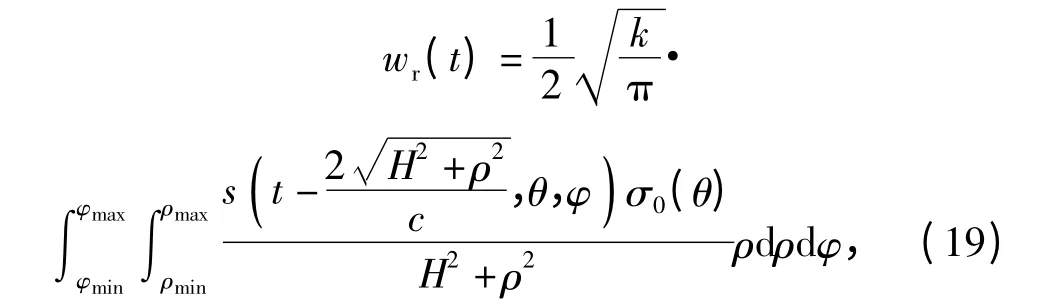
式中:ρ、φ 的积分上下限与天线入射角、天线波束宽度有关。

当弹丸垂直入射时，R = H/cos θ，ρ = Htan θ，假设天线半功率波束宽度为ϑa，(19)式可化简为

或

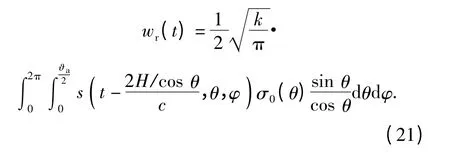
3 超宽带天线设计

为了得到超宽带无线电引信回波信号，应首先建立超宽带天线模型并求得超宽带天线参数，即(21)式中的s(t，θ，φ). 在电磁仿真软件CST 中，将两个完全相同的平面三角形对称振子天线平行放置，一个作为发射天线，一个作为接收天线，接收天线位于发射天线的最大辐射方向。天线模型图如图4所示。

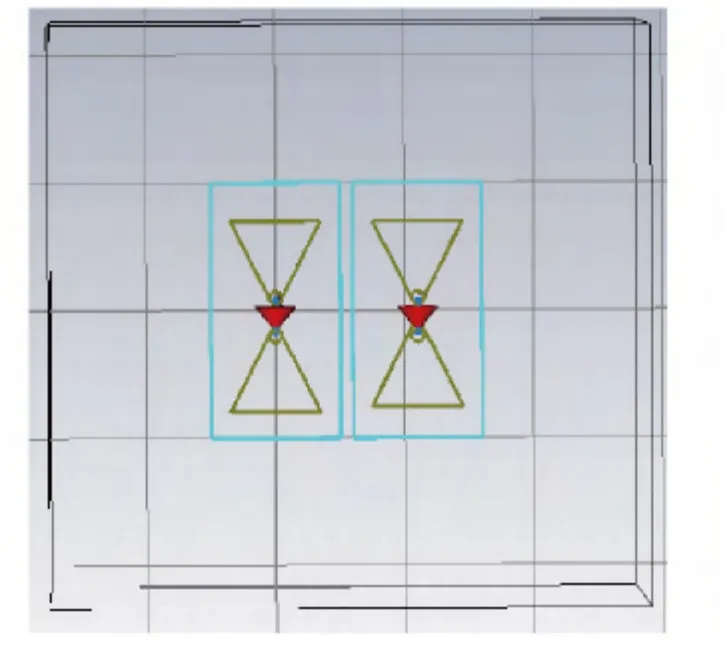
图4 超宽带天线模型Fig.4 Ultra-wideband antenna

发射天线激励信号为如图5所示的高斯2 阶导数，接收天线负载为50 Ω，发射天线与接收天线距离为2 mm 时，接收天线负载端天线辐射信号波形如图6所示［12］。

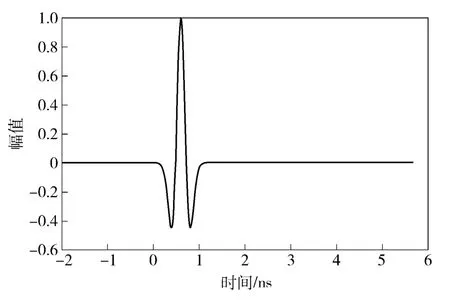
图5 天线激励信号Fig.5 Antenna excitation signal

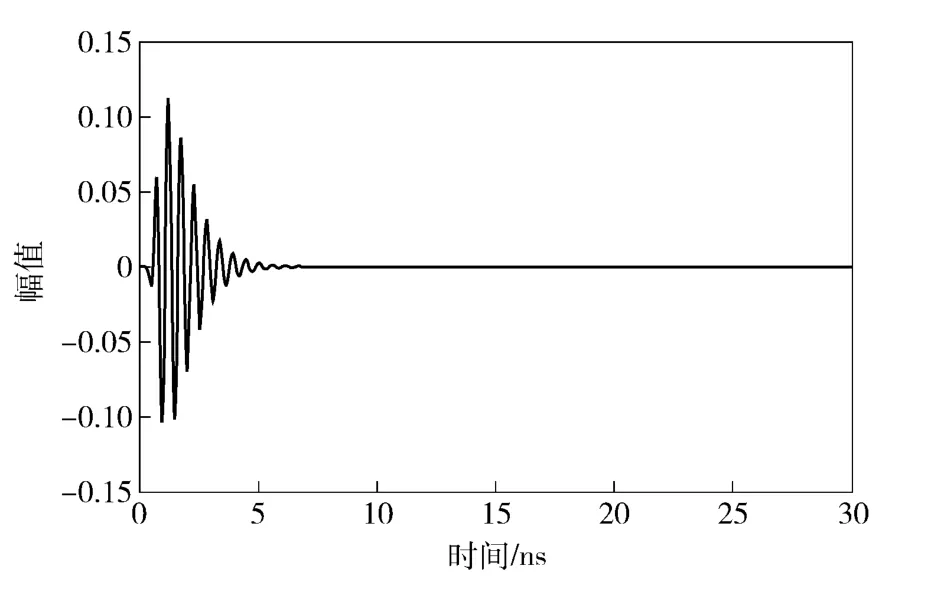
图6 天线辐射信号Fig.6 Antenna radiation signal

假设在天线半功率波束宽度内，σ0(θ)为常数σ0，忽略天线在不同辐射方向上辐射波形的不同，且F(t，r'，θ'，φ')=1，此时(20)式可简化为

4 超宽带无线电引信回波信号仿真与实测图形

4.1 仿真图形

根据第3 节中推导出的超宽带无线电引信平坦地面目标信号的(18)式，利用Matlab 仿真软件对其进行仿真，ϑa=60°时，改变引信距地面的高度H，得到目标信号如图7、图8所示。

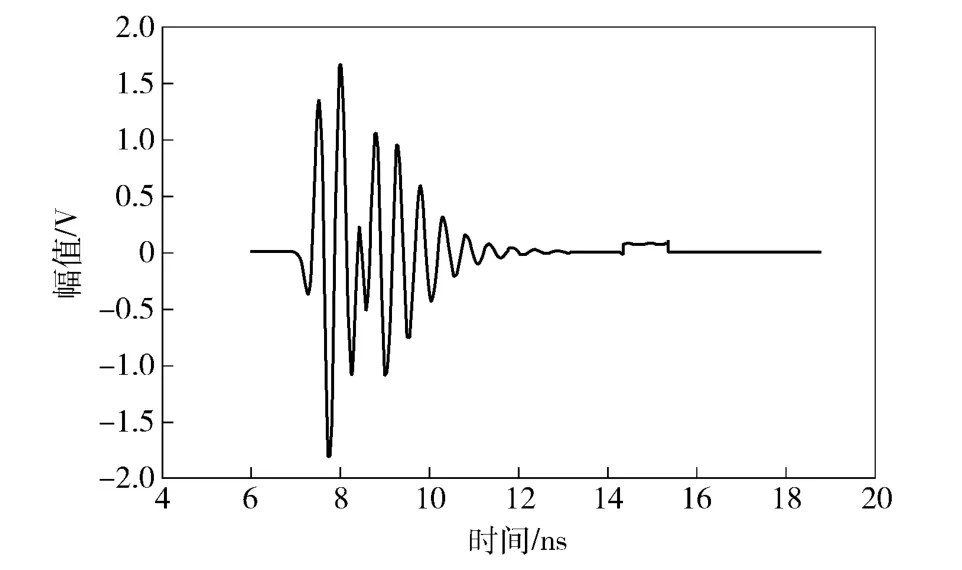
图7 H=1 m 时的回波信号Fig.7 Echo signal for H=1 m

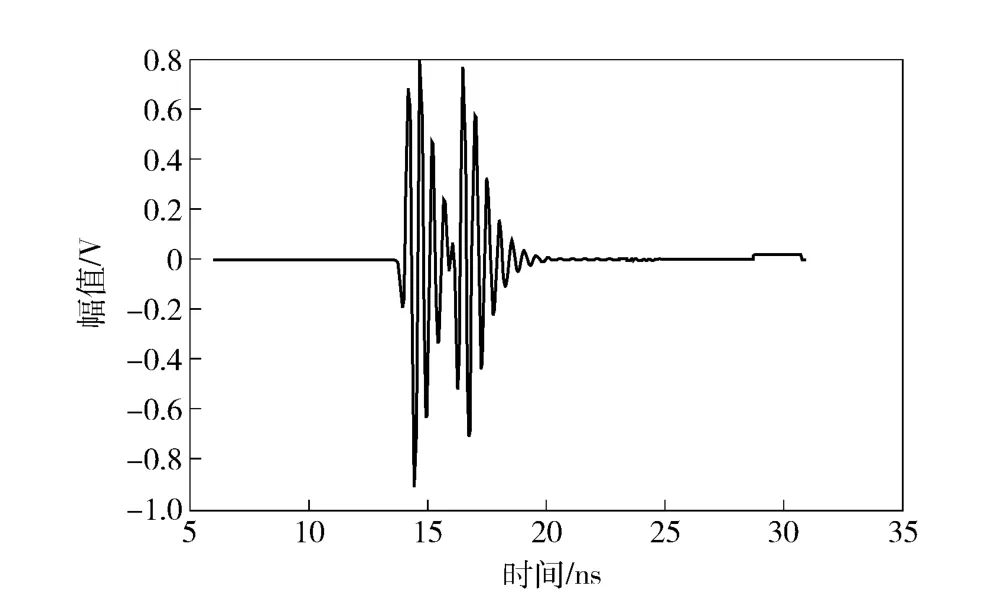
图8 H=2 m 时的回波信号Fig.8 Echo signal for H=2 m

由图7和图8仿真结果可见，随着H 的增加，回波信号的展宽效应明显，回波信号强度相应减少。

4.2 实测图形

实测条件:场地为室外水泥地面;温度25 ℃;引信起爆参数为检测回波信号第3 个高峰处引信启动;引信与地面落角为70° ～90°. 实测图形如图9、图10 所示。

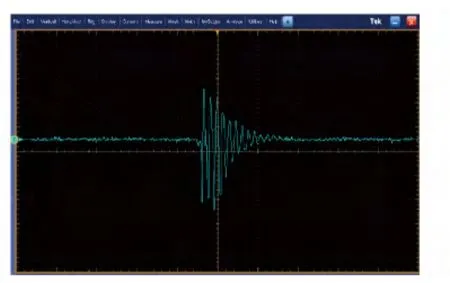
图9 H=1 m 时的回波信号Fig.9 Echo signal for H=1m

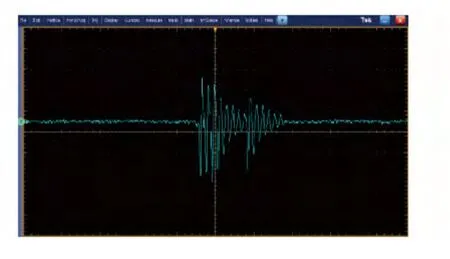
图10 H=2 m 时的回波信号Fig.10 Echo signal for H=2 m

由图9和图10 可见，随着H 的增加，回波信号的展宽效应明显，回波信号幅度相应减小。与仿真结果基本一致，验证了模型的正确性。

5 结论

本文旨在得出利用超宽带三角对称振子天线作为超宽带引信收发天线的对地超宽带无线电引信目标信号。通过对超宽带无线电引信目标信号的建模，得出以下结论:

1)在超宽带线性系统理论和平面三角形对称振子天线的研究基础上，从超宽带信号的多径效应出发，推导得出了超宽带无线电引信目标信号的数学模型并进行仿真，针对平坦地面采用积分的方法进行求解。

2)引信天线与天线波束照射范围内距离不同导致地面散射信号返回到天线的时间不同，从而造成展宽效应，随着引信目标距离地面高度H 不断增加，展宽效应明显。随着H 不断增加，回波信号幅度呈比例减少。

经过实际测试，仿真结果与实测结果基本一致。

References)

［1］Yildirim B S，Cetiner B A，Roqueta G，et al. Integrated bluetooth and UWB antenna［J］. Antennas and Wireless Propagation Letters，2009，8:149 -152.

［2］Zhang S W，Cui X. A novel second generation wavelet transform algorithm applied in laser radar echo signal denoising［C］∥2011 IEEE 3rd International Conference on Communication Software and Networks.Xi＇an:IEEE，2011:123 -126.

［3］Singh A K，Saxena R. Doppler estimation from echo signal using FRFT［J］. Wireless Personal Communications，2013，72(1):405 -413.

［4］潘曦，崔占忠. 无线电引信近场目标特性研究［J］. 兵工学报，2008，29(3):277 -281.PAN Xi，CUI Zhan-zhong. Near-field characteristic of target for radio fuze［J］. Acta Armamentarii，2008，29(3):277 - 281. (in Chinese)

［5］Ye L H，Chu Q X. 3.5/5.5 GHz dual band-notch ultra-wideband slot antenna with compact size ［J］. Electronics Letters，2010，46(5):325 - 327.

［6］张玉铮.近炸引信设计原理［M］. 北京:北京理工大学出版社，1996 ZHANG Yu-zheng. Proximity fuze design principles［M］.Beijing:Beijing Institute of Technology Press，1996.(in Chinese)

［7］科冈H M.雷达引信原理［M］.北京:国防工业出版社，1980.Korah H M. Radar fuze principles［M］.Beijing:National Defense Industry Press，1980.(in Chinese)

［8］张清泰.无线电引信总体设计原理［M］. 北京:国防工业出版社，1985.ZHANG Qing-tai. Radio fuze design principles［M］. Beijing:National Defense Industry Press，1985.(in Chinese)

［9］Chen S，Zhao H C，Zhang S N，et al. Study of ultra-wideband fuze signal processing method based on wavelet transform［J］. Radar，Sonar and Navigation，2014，8(3):167 -172.

［10］王全民，陈彬，郭刚，等. 超宽带冲激引信无线电引信地面回波仿真算法［J］. 系统仿真学报，2010，32(4):116 -120.WANG Quan-min，CHEN Bin，GUO Gang，et al. Ground echo simulation algorithm for ultra-wideband impulse-radio fuze［J］. Journal of System Simulation，2010，32(4):116-120.(in Chinese)

［11］Knott E F，Tuley M T ，Shaeffer J F. Radar cross section［M］.2nd ed. US:SciTech Publishing，2004.

［12］沈磊，黄忠华.超宽带无线电引信天线设计及仿真［J］. 兵工学报，2014，35(7):960 -964.SHEN Lei，HUANG Zhong-hua. Ultra-wideband optimization of radio antenna［J］.Acta Armamentarii，2014，35(7):960 -964.(in Chinese)