行星滚柱丝杠传动机构非线性建模与仿真
李强, 张佼龙, 周军, 高智刚
(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)
行星滚柱丝杠传动机构非线性建模与仿真
李强, 张佼龙, 周军, 高智刚
(西北工业大学 精确制导与控制研究所, 陕西 西安710072)
摘要:以行星滚柱丝杠为研究对象,针对伺服控制所关注的传动间隙和机构刚度2个非线性因素,建立了基于行星滚柱丝杠的摆动摇臂式弹载伺服系统传动机构非线性数学模型。重点建立了该传动机构的传动间隙模型、间隙动态计算模型及变刚度模型,结合行星滚柱丝杠运动学模型和摆动摇臂式传动机构传动模型,最终得到行星滚柱丝杠传动机构非线性数学模型。据此进行了带载条件下的伺服机构性能仿真,分析了间隙与刚度对伺服机构性能的影响,并使用性能向量法对不同传动间隙和组件刚度的影响进行了评价总结。
关键词:行星滚柱丝杠;间隙;刚度;性能向量;弹载伺服系统
行星滚柱丝杠具有承载能力和刚度更高,寿命更长,转速更高,体积更小的优异特性[1],使其成为大传动比弹载伺服系统传动机构的很好选择[2-3]。然而,若行星滚柱丝杠式伺服机构设计不当,传动间隙过大或传动刚度不足的问题会极大影响行星滚柱丝杠传动性能。目前,针对行星滚柱丝杠式传动机构的研究中尚无针对行星滚柱丝杠传动机构运动过程中刚度的动态变化进行建模和分析的成果发表。传动机构间隙方面的成果尚无在行星滚柱丝杠传动模型中引入多个间隙动态计算模型并仿真分析间隙对弹载伺服系统性能影响的成果发表。
本文旨在针对行星滚柱丝杠式弹载伺服传动机构建立考虑传动间隙和机构刚度两大非线性因素的数学模型。此模型既可用于高速、高过载、高作动频率下的弹载伺服系统仿真,又可用于分析各部位传动间隙和组件刚度对伺服机构性能的影响。
1行星滚柱丝杠理想传动模型
行星滚柱丝杠采用行星传动原理。滚柱既在丝杠驱动下自转,又随着滚柱保持架公转,从而将丝杠的旋转运动转化为螺母的直线运动,其径向剖面结构如图1所示。
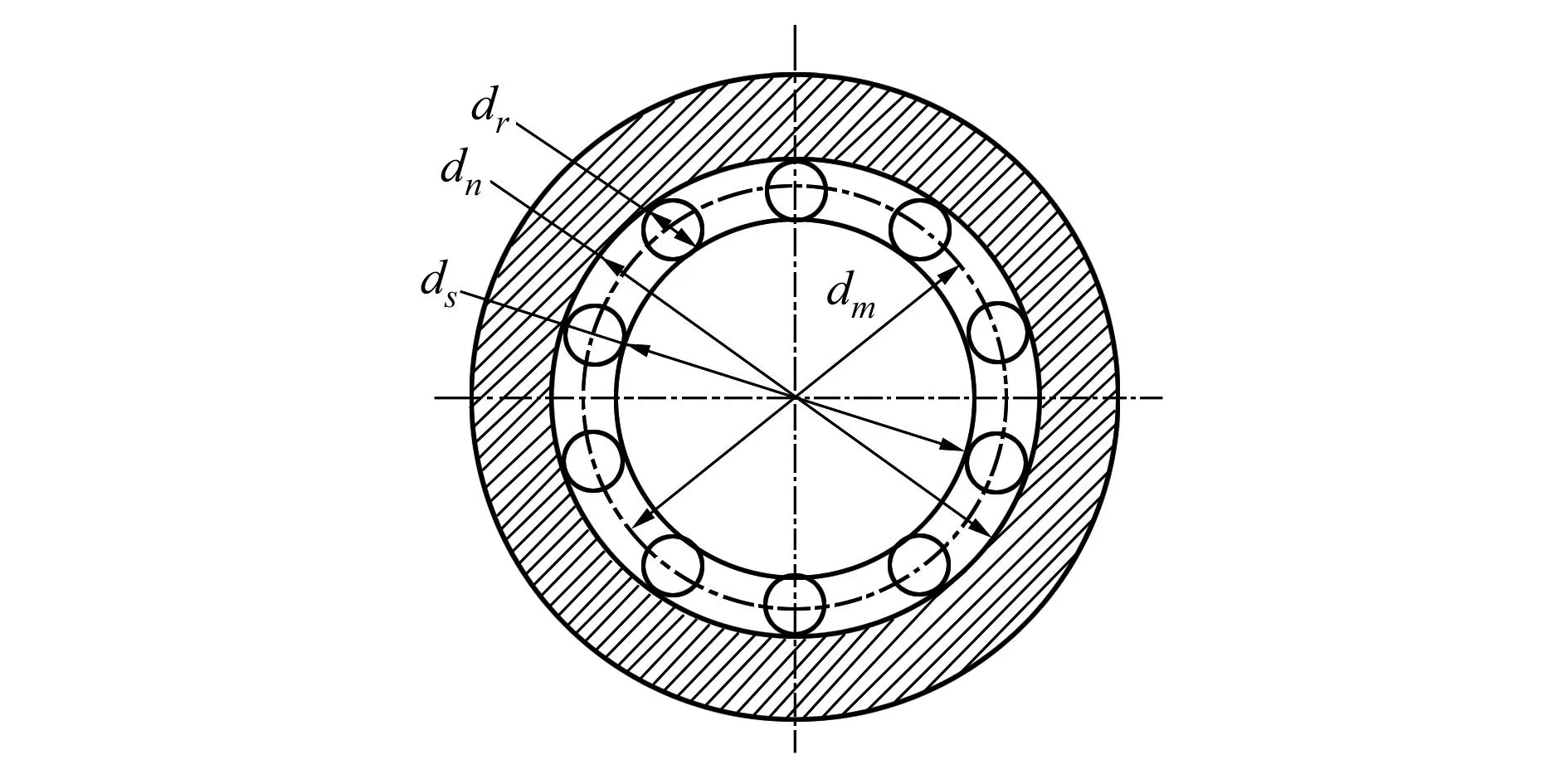
图1 行星滚柱丝杠径向剖面结构简图
若丝杠转动、螺母直线运动,则滚柱与螺母接触点为滚柱的速度瞬心,由速度瞬心法得:
(1)
式中,ω为丝杠角速度;ωμ为滚柱自转角速度;ω′为滚柱公转角速度。
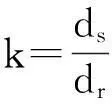
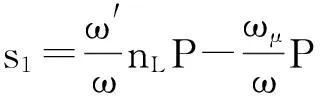

(2)
式中,P为螺距;s1为丝杠转动一周,滚柱相对螺母的轴向位移;s2为丝杠旋转一周,滚柱相对丝杠的轴向位移;ns为丝杠头数;nL为螺母头数。
由滚柱与螺母间无轴向相对运动得出:
(3)
同理,螺母转动、丝杠直线运动情况下的行星滚柱丝杠运动学模型为:
(4)
式中,H1为螺母旋转一周,滚柱相对丝杠的轴向位移;H2为螺母旋转一周,滚柱相对螺母的轴向位移。
由滚柱与丝杠间无轴向位移得出:
(5)
联立(2)式~(5)式得,螺母与丝杠相对转动一周产生的直线位移为:
(6)
2摆动摇臂式传动机构理想模型
行星滚柱丝杠的螺旋运动可以等效为图2所示运动。F1为丝杠公称半径处的作用力,其对丝杠的驱动力矩为T1;F2为丝杠转动时产生的轴向推力;α为丝杠导程角。
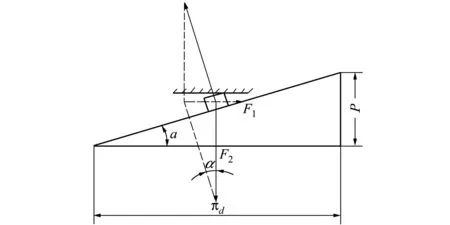
图2 滚柱丝杠副受载模型[4]
定义摆动摇臂式伺服机构中行星滚柱丝杠副组件(AB段)与摇臂(BC段)垂直时为伺服系统零位,则伺服系统受力模型可等效为图3所示。

图3 伺服系统等效受力模型
由力学平衡与几何关系得出机构受载模型为:
(7)
式中,ρ为当量摩擦角;η为正传动效率;b、a、l、δ分别为伺服机构长度、零位长度、摇臂长度及舵偏角。
由(7)式得出伺服电机的驱动力矩:
(8)
故伺服机构传动比为:
(9)
3传动间隙建模及动态计算
根据各组件的相对运动关系可知,行星滚柱丝杠传动机构中的间隙主要出现在以下4个位置:
1) 电机与主丝杠连接间隙,定义为δ1;
2) 行星滚柱丝杠传动间隙,定义为δ2;
3) 支撑轴承安装支耳间隙,定义为δ3;
则电机克服以上间隙所要转动的角度为:
(10)
以上模型给出了4处间隙的最大值。由于弹载伺服系统高频往复的作动特性,各间隙在零至最大值之间动态变化,且多间隙共同作用的结果并非每个间隙作用的简单叠加。因此需要根据伺服机构的运动状态,进行传动间隙动态计算,方法如下:
1) 在时刻ti判断间隙模型输入速度ωin和加速度αin方向。若ωin、αin同向,标识符Pi=1,反之Pi=-1。
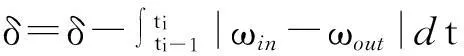

4) 若δ≤0,速度输出跟踪速度输入;否则,间隙模型输出速度保持不变。
通过在(10)式中各间隙对应的传动比后引入该动态计算模型即可实现多间隙动态计算。
反应寿险需求的指标较多,在这里我们考虑数据的可得性和人口数量对寿险需求的影响,选取人均寿险保费收入(元)Y来作为被解释变量。
4传动机构刚度分析与建模
设圆锥滚子轴承、上下支耳、螺母、丝杠、螺牙、摇臂受到轴向力F作用产生的轴向变形分别为Δ1、Δ2、Δ3、Δ4、Δ6、Δ7;螺母相对于丝杠的轴向变形为Δ5;丝杠在电机扭矩T作用下发生扭转变形Δθ1;输出轴受铰链力矩M作用产生扭转变形Δθ2。则可将以上变形根据部件组成分为五类:(1)丝杠支撑轴承及上下支耳变形Δ1Δ2;(2)丝杠螺母轴向变形Δ3Δ4Δθ1;(3)滚柱与丝杠、滚柱与螺母接触变形Δ5Δ6;(4)摇臂变形Δ7;(5)输出轴变形Δθ2。
其中,Δ5由螺母和丝杠分别相对于滚柱的轴向变形量组成,为接触变形,可根据赫兹变形理论得出;除Δ5外的变形可根据受载分析得出。
最终建立起基于行星滚柱丝杠的摆动摇臂式传动机构刚度模型为:
(11)
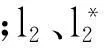
根据(7)式,机构长度b随舵偏角δ变化,因此刚度随伺服机构作动是动态变化的。将舵偏角δ和轴向力F作为输入变量,采用与间隙引入相似的方法将(11)式所示刚度模型引入行星滚柱丝杠传动机构理想模型后,即可实现行星滚柱丝杠传动机构刚度的动态解算。
5性能坐标与性能向量
为评价和分析不同非线性因素对系统性能的影响,需要定义统一的性能评价指标。这里提出性能坐标和性能向量的概念,并给出归一化范数表达式。
定义:
性能坐标:设系统A存在特性P1、P2、P3、…、Pn,其相应的归一化性能指标p1、p2、p3、…、pn∈C,则定义(p1,p2,p3,…,pn)∈Cn为系统A特性P1、P2、P3、…、Pn的性能坐标。
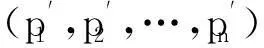
基于性能向量的概念,可以利用性能向量的范数来定量衡量系统性能的变化。为消除各性能指标量纲不同对评价结果的影响,给出经过归一化处理的范数表达式:
(12)
式中,下标j表示不同的系统。
对于机电伺服系统研制过程中关注的系统幅频特性和动态特性,定义带宽为x,上升时间为y。
6仿真分析与评价
仿真过程中采用弹性负载力矩模拟舵面气动力矩的负载特性,传动间隙和组件刚度影响下,伺服系统频带特性曲线如图4所示,方波指令下速度曲线如图5所示。
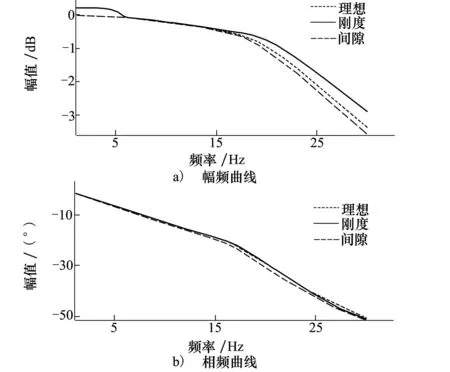
图4 间隙、刚度影响下的系统Bode图

图5 方波指令下的系统速度曲线
用性能向量法分析各主要传动间隙和组件刚度对系统性能的影响,结果如表1所示。
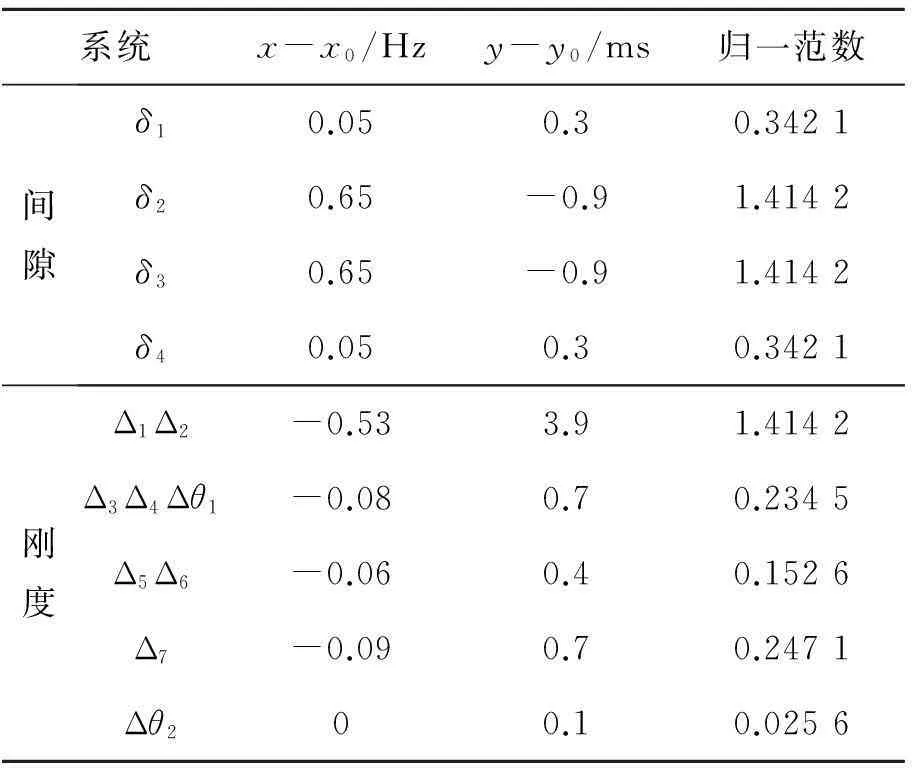
表1 间隙及刚度对系统性能的影响
分析上述仿真图表可得以下4点结论:
1)间隙对系统频带性能的影响表现为低频段和高频段系统增益的增大;而刚度的影响为全频段系统响应幅值衰减、相位滞后。
2)受刚度不足影响,系统响应速度下降,上升时间延长。间隙影响表现在速度调节呈阶梯状变化,且达到稳态后速度曲线呈方波状振荡。
3)各传动间隙对系统性能综合影响大小顺序为:行星滚柱丝杠传动间隙≈丝杠支撑轴承与支耳游隙>电机与丝杠传动间隙≈限位轴承与导向槽间隙。
4)各组件刚度对系统性能影响大小为:支撑轴承及支耳刚度>摇臂刚度>丝杠螺母轴向刚度>行星滚柱丝杠接触刚度>输出轴刚度。
7结论
针对弹载伺服机构高速、高过载、高作动频率的工作特性,本文基于行星滚柱丝杠运动学及受载分析,建立了行星滚柱丝杠传动机构理想模型。在此基础上,考虑传动间隙和组件刚度2个非线性因素,建立了各部位传动间隙模型、间隙动态计算方法和各组件变刚度模型,按照运动传递关系将其引入理想模型,完成了行星滚柱丝杠传动机构的非线性建模。本文在仿真分析间隙和刚度对系统性能影响的基础上,以性能向量衡量各传动间隙及不同组件刚度对系统性能的影响。
参考文献:
[1]Velinsky S A. Kinematics and Efficiency Analysis of the Planetary Roller Screw Mechanism[J]. Journal of Mechanical Design, 2009, 131(1):1-8
[2]Lemor P C. The Roller-Screw, an Efficient and Reliable Mechanical Component of Electro-Mechanical Actuators[C]//Proceedings of the 31st Intersociety, 1996: 215-220
[3]Wander J. Initial Disturbance Accommodating Control System Analysis for Prototype Electromechanical Space Shuttle Steering Actuator[C]//Proceedings of the American Control Conference, 1995: 3961-3964
[4]张佼龙, 周军, 周凤岐. 滚珠丝杠舵机应用问题研究[J]. 机械与电子, 2011(10):15-19
Zhang Jiaolong, Zhou Jun, Zhou Fengqi. Application Study on Ball Screw Actuator[J]. Machinery & Electronics, 2011(10):15-19 (in Chinese)
Nonlinear Modeling and Simulation of a Planetary Roller Screw
Based Transmission
Li Qiang, Zhang Jiaolong, Zhou Jun, Gao Zhigang
(Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi′an 710072, China)
Abstract:In this paper, the planetary roller screw (PRS) is studied through focusing on the nonlinear factors of clearance and stiffness to constitute a nonlinear model of a PRS based transmission. By combining the focally constructed models of clearances, dynamic calculation of clearance and variable stiffness with those of PRS mechanism and transmission, the proposed nonlinear model is established. After simulating the effects of overall clearance and compliance, performance vector is applied to collating effects of various clearances and compliances across the mechanism for further analysis.
Key words:angular velocity, Bode diagrams, calculations, computer simulation, friction, kinematics, mathematical models, mechanisms, servomotors, stiffness, transmissions, vectors; clearance, missile-borne servo systems, performance vector, planetary roller screw
中图分类号:TP391.9
文献标志码:A
文章编号:1000-2758(2015)05-0739-05
作者简介:李强(1990—),西北工业大学博士研究生,主要从事导弹及航天器制导与控制、电动伺服系统控制研究。
收稿日期:2015-04-16

