伪卫星空中基站定位高性能算法研究
阎海峰, 魏文辉, 冯志华, 高社生
(1.西北工业大学 自动化学院, 陕西 西安 710072; 2.中航工业 深圳市南航电子工业有限公司, 广东 深圳 518000)
伪卫星空中基站定位高性能算法研究
阎海峰1,2, 魏文辉1, 冯志华1, 高社生1
(1.西北工业大学 自动化学院, 陕西 西安710072; 2.中航工业 深圳市南航电子工业有限公司, 广东 深圳518000)
摘要:伪卫星作为卫星导航系统的重要增强手段,能够克服卫星系统在导航定位及武器精确制导方面存在的缺点。针对伪卫星空中基站位置不易精确确定的问题,设计了临近空间伪卫星空中基站定位SINS/CNS/SAR组合导航系统,建立了组合导航非线性数学模型;在吸收抗差自适应滤波、高斯滤波和粒子滤波优点的基础上,提出了一种抗差自适应高斯混合Sigma点粒子滤波算法。将提出的算法应用于SINS/CNS/SAR自主导航系统进行计算仿真,并与Unscented卡尔曼滤波和粒子滤波比较,结果表明:提出的新算法能够满足伪卫星空中基站自主导航定位的需求,导航精度明显高于Unscented卡尔曼滤波和粒子滤波算法。
关键词:伪卫星空中基站;自主组合导航;抗差自适应滤波;粒子滤波
卫星系统的发展,给科学研究、人民生活和国防建设带来了巨大的革命性影响,然而它存在以下缺陷:由于卫星定位的精确性和可靠性严重依赖可见星的数量和几何分布状况,因此,在机场、峡谷、室内和地下等观测环境较差的地域,可见星的数量和几何布局通常无法满足应用的需要[1-2];卫星定位系统自身存在着信号易被遮挡、干扰等弊端[3-4];随着科学技术水平的提高,各种反卫星技术不断涌现,对卫星导航技术构成了严重威胁。而采用伪卫星辅助卫星定位,可以改善卫星系统的定位精度、可用性和可靠性,满足用户需求。
以浮空器为空中基站的临近空间伪卫星,不但有更大的覆盖区域、更长的滞留时间和不容易被攻击等优点,而且在耗资、响应性、灵活性、分辨率及生存性等方面都具有显著优势。因此,以浮空器为平台的伪卫星是当前区域定位系统发展的趋势[6-7]。但浮空器在临近空间并非绝对静止,当临近空间伪卫星对用户定位时,其自身存在的位置误差和由其他误差源所引起的误差会影响到用户最终的定位精度。因此,需要对临近空间伪卫星空中基站的位置精度做进一步研究[5,7]。
本文研究临近空间伪卫星空中基站自身位置的精确确定及高性能算法设计与仿真。首先,设计捷联惯导系统(SINS)/天文导航系统(CNS)/合成孔径雷达(SAR)自主组合导航系统,建立适用于临近空间伪卫星的自主导航非线性数学模型;然后,提出一种新的抗差自适应高斯混合Sigma点粒子滤波算法;最后进行仿真计算和算法性能分析与比较。
1伪卫星空中基站定位组合导航数学模型设计
SINS是一种自主式导航系统,仅依靠系统本身就能在全球范围内实现全天候、自主、隐蔽、连续的三维定位和定向,但其缺点是导航误差随时间积累。SAR具有全天候和全天时工作、自主性强等优点[8]。SAR提供的水平位置和航向角信息可用来修正SINS随时间积累的导航误差。但这种修正不仅受地标数目的限制,而且数据更新率慢(一般在100 s左右),在海洋、沙漠等地面特征不明显的区域,SAR还会失去对SINS的修正能力,这使单纯的SINS/SAR组合导航系统的应用受到限制[8-9];CNS以已知准确的空间位置和不可毁灭的恒星作为导航信息源,自主性强、定位精度高,但其缺点是易受气候影响[10]。将CNS、SINS与SAR三者组合,构成SINS/CNS/SAR自主组合导航系统,能够兼备SINS、CNS和SAR三者的优点,相互取长补短,不但抗干扰能力强、而且自主性能好,定位精度高,非常适合临近空间飞行器对导航系统性能的要求[11]。
SINS/CNS/SAR自主组合导航原理如图1所示。
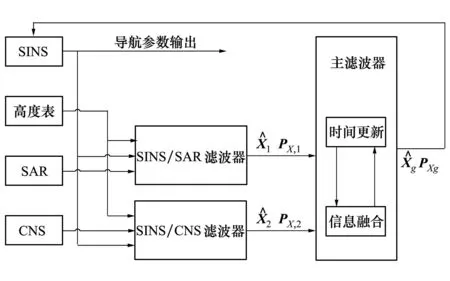
图1 SINS/CNS/CNS自主组合导航原理图
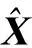
(1)
(2)
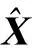
1) 系统状态方程
选取东北天地理坐标系为导航坐标系,通过对组合系统的性能进行分析,建立非线性系统的状态方程为

(3)
式中,g(X(t),t)为非线性函数,G(t)为噪声系数阵,X(t)系统状态变量,w(t)为系统噪声。在自主组合系统中,引入高度表提供高度信息,状态变量选为
(4)
式中,(δvE,δvN,δvU)为速度误差,(δφ,δλ,δh)为位置误差,(φE,φN,φU)为姿态角误差,(εx,εy,εz)为陀螺常值漂移,(X,Y,Z)为加速度计零偏,δhb为高度表偏置。
系统噪声阵表示为
(5)
式中,(wεx,wεy,wεz)为陀螺仪常值漂移,(εmx,εmy,εmz)为陀螺一阶马尔科夫漂移,(wx,wy,wz)为加速度计常值漂移,whb为高度表常值漂移。
2) 系统量测方程
在SINS/SAR导航子系统中,将SINS输出的航向角信息和位置信息与SAR输出的航向角信息、水平位置信息以及高度表输出的载体高度信息的差作为量测量,则量测量可以表示为
(6)
式中,ψI、LI、λI和hI分别为SINS输出的航向角、纬度、经度和高度信息,ψS、LS和λS分别为SAR输出的航向角、纬度和经度信息,he为高度表输出的高度信息,δ·表示各项对应的误差。
可得SINS/SAR组合导航系统的量测方程为
(7)
式中,e1(t)为SAR的量测噪声,h1(X(t),t)为量测矩阵,这里为非线性函数。
在SINS/CNS导航子系统中,选取SINS输出的载体姿态四元数和位置信息与CNS输出的载体姿态四元数和水平位置信息,以及高度表输出的载体高度信息之差作为量测量,则量测量可以表示为
(8)
式中,qI0、qI1、qI2、qI3为惯导系统输出的姿态四元数,LI、λI、hI分别为惯导系统输出的纬度、经度和高度信息;qC0、qC1、qC2、qC3为天文导航系统输出的姿态四元数,LC、λC分别为天文导航输出的纬度和经度信息;he为气压高度表输出的高度信息;δ·表示各项对应的误差。
可得SINS/CNS导航子系统的量测方程为
(9)
式中,e2(t)为CNS的量测噪声,h2(X(t),t)为量测矩阵。
2抗差自适应高斯混合Sigma点粒子滤波
抗差自适应高斯混合Sigma点粒子滤波算法对状态向量的估计值进行Sigma点展开,并通过抗差等价权和自适应因子调节状态均值和方差来抑制噪声干扰,在时间更新和量测更新步骤中,利用高斯混合密度形式获得接近真实分布的重要性密度函数。该算法是综合了高斯混合滤波与重要性采样技术的一种改进粒子滤波方法,其中高斯混合滤波过程中高斯近似分布的计算是以抗差自适应Sigma点卡尔曼滤波方法为基础的。考虑非线性动态系统
(10)
式中,xk,yk∈Rn分别为k时刻系统的状态向量和量测向量,vk,nk∈Rn分别为系统噪声和量测噪声,f(·)和h(·)为非线性函数。抗差自适应Sigma点卡尔曼滤波算法的主要步骤可描述如下。

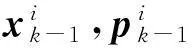
(11)
式中,λ=α2(n+ν)表示尺度因子,ν为二阶尺度因子,N为采样粒子个数,α决定采样点对预测均值的分散程度,β一般根据先验知识来取值(对于高斯分布最佳取值为2),Wj表示第j个Sigma点的权值,满足∑Wj=1,j=0,1,…2N。利用UKF算法对粒子进行预测和更新。
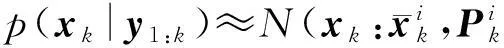
(12)
式中,k
0
子选取如下
(13)
者都是重要的调节因子。前者通过对残差的判断来选取,而后者根据状态估计值与预报值之差来选取。
然后依据卡尔曼滤波框架进行回归递推得到
(14)
(15)
(16)
4)返回步骤2)
抗差自适应高斯混合Sigma点粒子滤波算法在时间更新和量测更新步骤中,利用高斯混合密度形式,获得更好的预测概率密度函数和近似后验概率密度函数。通过抗差等价权和自适应因子对状态噪声和量测噪声的调节,预测概率密度函数和近似后验概率密度函数可以在量测更新过程中达到对状态的最小方差准则下的最优估计,由此得到的均值和方差能表述真实密度函数的性质。提出的抗差自适应高斯混合Sigma点粒子滤波的主要步骤如下。
初始预测概率密度函数的N个高斯混合形式表示为
(17)
3) 计算近似后验概率密度函数,作为粒子重要性密度函数。
(18)
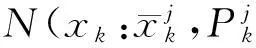
(19)
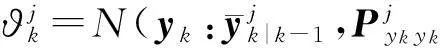
4) 计算粒子权值
(20)
5) 该算法是以高斯形式逼近所求的密度函数,即对获得的状态估计均值和协方差随时间递归更新,可以利用EM或WEM(weightedexpectationmaximization)方法使估值收敛到最优值上,代替重采样步骤。将采样粒子拟合为平滑的参数分布,然后从该分布中进行采样得到新的样本。
WEM方法可表示为
(21)
(22)
WEM和EM步骤避免了从大量的粒子中进行重采样处理,减轻了粒子退化现象和适当降低了计算复杂度。
6) 与计算近似后验概率密度步骤相似,预测概率密度函数表示为
(23)
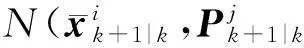
7) 返回步骤2)。
由上述步骤可以看出抗差自适应高斯混合Sigma点粒子滤波算法利用抗差自适应因子调节得到粒子状态均值和方差,并利用有限的高斯混合模型来得到近似后验概率密度的重要性密度函数,考虑了最新量测的影响,并减小非高斯噪声、系统模型等带来的误差干扰,可以更好的表述真实密度分布的性质,提高了粒子滤波算法的性能。
3实验与分析
将提出的抗差自适应高斯混合Sigma点粒子滤波算法(RAGMSPPF)应用于伪卫星空中基站SINS/CNS/SAR自主导航系统中进行性能验证,并与传统的Unscented卡尔曼滤波(UKF)和粒子滤波(PF)进行比较。
实验数据来源于某型号无人机的测试飞行。该无人机经过8min的初始化后起飞,整个测试飞行过程持续约96min。由地面观测站和GPS联合记录无人机各种飞行数据作为参考值,包括位置、速度和姿态等导航信息;由无人机自身存储相关飞行参数信息以及量测信息,数据更新率100Hz。截取无人机某段飞行过程的飞行数据作为实验数据来源。初始位置经度E108.997°,纬度N34.246°,高度2 000m,飞行持续时间1 000s,平均速度150m/s,飞行轨迹如图2所示。SINS、CNS和SAR的仿真参数设置如表1所示。滤波初始位置误差1m,速度误差0.1m/s,姿态误差100″。

图2 截取的无人机飞行轨迹
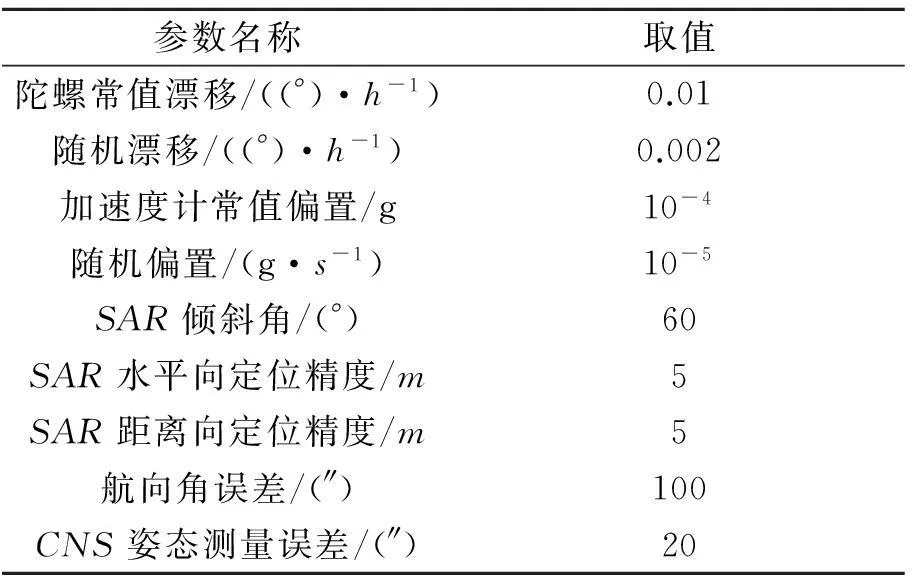
参数名称取值陀螺常值漂移/((°)·h-1)0.01随机漂移/((°)·h-1)0.002加速度计常值偏置/g10-4随机偏置/(g·s-1)10-5SAR倾斜角/(°)60SAR水平向定位精度/m5SAR距离向定位精度/m5航向角误差/(″)100CNS姿态测量误差/(″)20
将SINS/CNS/SAR自主导航系统获得的导航信息与参考飞行数据之差作为仿真结果,验证该自主导航系统模型及非线性滤波算法的性能。仿真结果如图3~图5所示。

图3 自主组合导航系统经度误差 图4 自主组合导航系统纬度误差 图5 自主组合导航系统高度误差
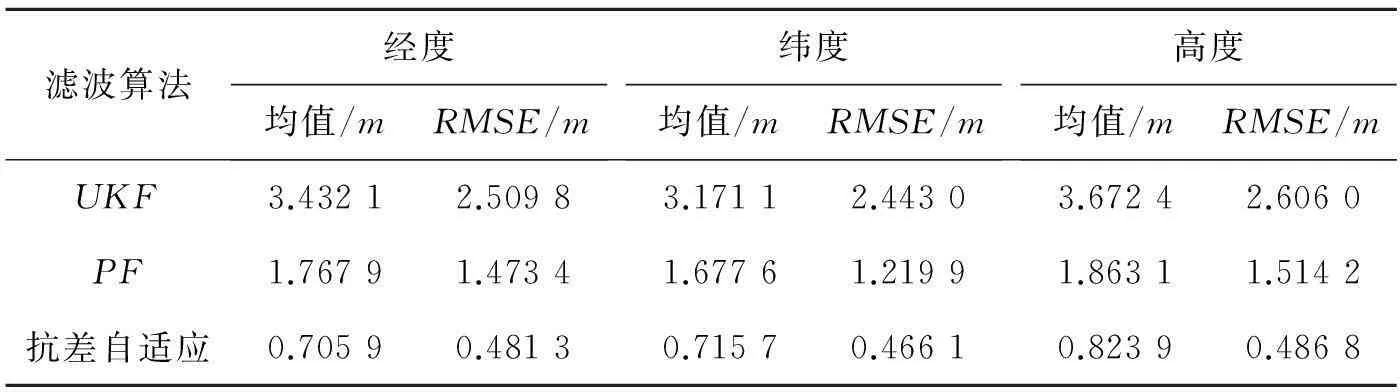
滤波算法经度均值/mRMSE/m纬度均值/mRMSE/m高度均值/mRMSE/mUKF3.43212.50983.17112.44303.67242.6060PF1.76791.47341.67761.21991.86311.5142抗差自适应0.70590.48130.71570.46610.82390.4868
由图3~图5可以看出,Unscented卡尔曼滤波算法的位置误差在10m以内,粒子滤波算法的位置误差在5m以内,而本文提出的抗差自适应高斯混合Sigma点粒子滤波算法的位置误差可以控制在2.5m以内,其性能明显优于其他2种滤波算法,提高了自主组合导航系统的精度。表2的误差统计结果也证明了该算法的优越性。
4结论
临近空间伪卫星具有机动灵活、成本低等优点,一旦受到敌方破坏,能在战场上空迅速部署、快速发射,立即补充,满足高科技战争空间应急导航定位的需要。因此,以浮空器为平台的伪卫星是当前区域定位系统发展的趋势。SINS/CNS/SAR自主组合导航系统兼备了SINS、CNS和SAR的优点,抗干扰能力强,自主性好,导航精度高。本文设计了临近空间伪卫星空中基站SINS/CNS/SAR自主组合导航系统,建立了自主导航非线性数学模型;在吸收抗差自适应滤波、高斯滤波和粒子滤波优点的基础上,提出了一种新的抗差自适应高斯混合Sigma点粒子滤波算法。研究结果表明,提出的算法能满足临近空间伪卫星对自主组合导航滤波解算精度的要求,解算精度明显高于Unscented卡尔曼滤波和粒子滤波算法。
参考文献:
[1]田世君,皮亦鸣,周钰. 基于伪卫星的改善GPS几何精度因子的研究[J]. 测绘科学,2008,33(5):62-64
TianShijun,PiYiming,ZhouYu.ResearchonImprovingGPSGeometricDilutionofPrecisionbyPseudolite[J].ScienceofSurveyingandMapping, 2008, 33(5): 62-64 (inChinese)
[2]胡胜军,王玮,张京娟,等. 伪卫星进近着陆系统几何布局研究[J]. 宇航计测技术,2010,30(5):54-57
HuShengjun,WangWei,ZhangJingjuan,etal.GeometryResearchonthePseudolite-BasedApproachandLandingSystem[J].JournalofAstronauticMetrologyandMeasurement, 2010, 30(5): 54-57 (inChinese)
[3]戴邵武,马长里,代海霞. 北斗二代/SINS组合导航系统研究[J]. 全球定位系统,2010(1):25-29
DaiShaowu,MaChangli,DaiHaixia.ResearchofBeidouII/SINSIntegratedNavigationSystem[J].GNSSWorldofChina, 2010(1): 25-29 (inChinese)
[4]李罡,王志明,吕晶. 卫星导航技术专题讲座(二),第3讲,我国卫星导航定位系统简介[J]. 军事通信技术,2009,30(4):94-97
LiGang,WangZhiming,LüJing.SummaryofSatelliteNavigationPositioningSysteminChina[J].JournalofMilitaryCommunicationsTechnology, 2009, 30(4): 94-97 (inChinese)
[5]呼玮,杨建军,何萍. 基于临近空间飞艇定位的伪卫星布局研究[J],无线电工程,2009,39(10):24-27
HuWei,YangJianjun,HePing.StudyonPseudoliteConfigurationSchemeBasedonNearSpaceAirships[J].RadioEngineeringofChina, 2009, 39(10): 24-27 (inChinese)
[6]YarlagaddaR,AliI,HersheyJ.GPSGDOPMetric[J].IEEProceedingsRadar,SonarandNavigation, 2000, 147(2):259-264
[7]王玮,刘宗玉. 伪卫星空中基站的定位算法研究[J]. 宇航计测技术,2010,30(1):15-19
WangWei,LiuZongyu.ThePositioningAlgorithmforAirbornePseudolites[J].JournalofAstronauticMetrologyandMeasurement, 2010, 30(1): 15-19 (inChinese)
[8]GaoShesheng,ZhongYongmin,LiWei.RobustAdaptiveFilteringMethodforSINS/SARIntegratedNavigationSystem[J].AerospaceScienceandTechnology, 2011, 15(6):425-430
[9]王小旭,赵琳. 自适应融合滤波算法及其在INS/GPS组合导航中的应用[J]. 宇航学报,2009,31(11):2503-2511
WangXiaoxu,ZhaoLin.AdaptiveFusionFilteringAlgorithmandItsApplicationforINS/GPSIntegratedNavigationSystem[J].JournalofAstronautics, 2009, 31(11): 2503-2511 (inChinese)
[10] 郁丰,熊智,屈蔷. 基于多圆交汇的天文定位与组合导航方法[J]. 宇航学报,2011,32(1):88-92
YuFeng,XiongZhi,QuQiang.MultipleCircleIntersection-BasedCelestialPositioningandIntegratedNavigationAlgorithm[J].JournalofAstronautics, 2011, 32(1): 88-92 (inChinese)
[11]GaoShesheng,GaoYi,ZhongYongmin,WeiWenhui,RandomWeightingEstimationMethodforDynamicNavigationPositioning[J].ChineseJournalofAeronautic, 2011, 24(3):318-323
Research on High-Performance Algorithm for
Pseudolite Air Based Positioning
Yan Haifeng1,2, Wei Wenhui1, Feng Zhihua1, Gao Shesheng1
Abstract:Pesudolite, as an important means to enhance the satellite navigation system, can overcome the disadvantage of satellite navigation system in terms of positioning and precision-guided weapons. For pseudolites air based positioning that is not easy to accurately determine the location, we design a SINS/CNS/SAR integrated navigation system for the air based positioning of near space pseudolite, and the non-linear mathematical model of the system is established. On the basis of absorbing the merits of robust adaptive filtering, Gaussian filtering and particle filtering, a robust adaptive Gaussian mixture sigma point particle filter algorithm is proposed. Then, the proposed algorithm is applied to SINS/CNS/SAR autonomous navigation system for calculation and simulation and the results are compared with those of unscented Kalman filtering and particle filtering. The results and their analysis show preliminarily that the new algorithm can meet the needs of autonomous navigation positioning of the pseudolite air based and the navigation accuracy is significantly higher than those of the unscented Kalman filtering and particle filtering algorithms.
Key words:acceleration, adaptive filtering, calculations, computer simulation, covariance matrix, design, errors, estimation, information fusion, mathematical models, navigation, probability density function, velocity; autonomous navigation, particle filtering, pseudolite air base, robust adaptive filtering
中图分类号:V249.3
文献标志码:A
文章编号:1000-2758(2015)05-0763-07
作者简介:阎海峰(1964— ),西北工业大学博士研究生,主要从事导航制导与控制、控制理论与控制工程等研究。
基金项目:国家自然科学基金(61174193)资助
收稿日期:2015-04-01

