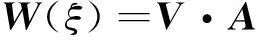小型固定翼无人机多步长在线风场估计
屈耀红, 于丽丽, 周迎, 袁冬莉
(西北工业大学 自动化学院, 陕西 西安 710072)
小型固定翼无人机多步长在线风场估计
屈耀红, 于丽丽, 周迎, 袁冬莉
(西北工业大学 自动化学院, 陕西 西安710072)
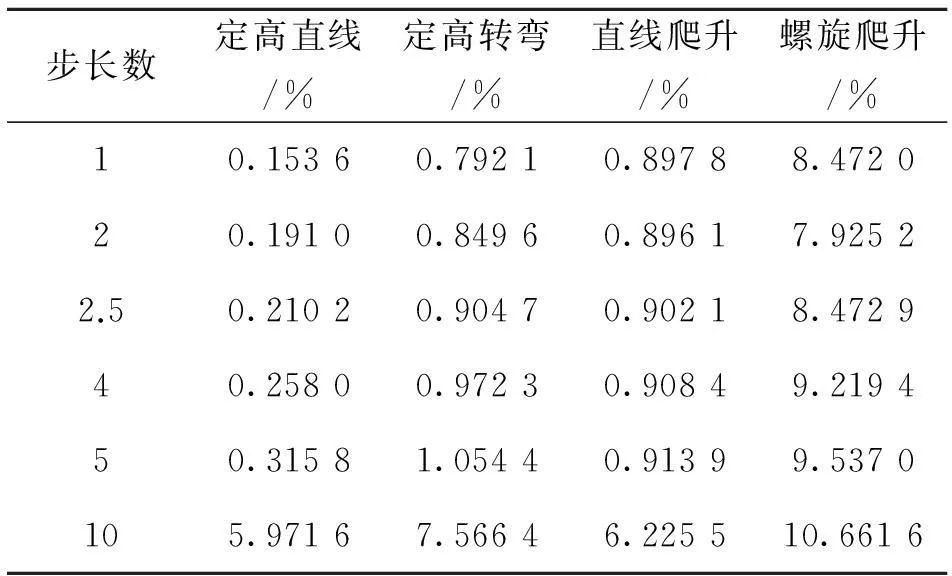
摘要:基于小型固定翼无人机飞行运动位置矢量关系,提出了一种多步长推算的风场估计方法,并通过飞行试验数据定量分析了步长数对估计精度的影响。该方法利用无人机飞行位置信息得到基于GPS/DR的风矢量场估计模型,接着通过飞行试验得到无人机在4种不同运动模态下飞行时,此风场估计方法获取风信息的步长数的最佳阈值。仿真结果表明,无人机以120~150 m/s飞行速度回旋飞行、飞行数据采样步长取为1 s的情况下,步长数不大于5 h的多步长风场估计方法可以最准确地估计出风信息,其测量风速误差不超过10%。
关键词:无人机;风场估计;步长;飞行试验;GPS/DR;飞行位置
大气测量及风场估计技术是无人机探空领域的重要研究课题[1],受风场复杂性、观测持久性及机载风测量设备精度的影响,大气风场的精确估计一直是探空领域的重大难题。目前对风场的研究工作主要集中在风数据的统计校正分析及风矢量的建模估计2个方面。
风数据的统计校正主要包括对风信息的长期观察分析[2]、对风探测数据的校准[3]以及对大气测量不确定度的研究[4],此外,也可对测量数据进行整合,建立大气状态观测的实时数据库[5]。此类工作实现了对大气数据的探测、收集和统计,以及对风场信息的深入分析及校准,为风场的建模分析及研究工作提供了充足的理论数据和实践基础。
风矢量的建模估计则是利用了气象无人机的 飞行位置的矢量三角形关系进行的。由于无人机飞行过程中受到多种干扰和威胁[6],而风作为主要大气环境,是影响无人机沿预定航路飞行的主要干扰,因此风场估计[7]及风信息修正[8]可借助无人机飞行航迹的三角形关系求取偏差完成。除了仿真模拟,风信息估计工作也可利用实测风数据完成,如文献[9] 和文献[10]利用无人机试飞数据建立飞机模型,并进一步完成了风估算方法设计及精度研究。
对风场的测量及对风场估计算法的研究日趋具体化和深入化,尤其基于矢量三角形的风场估计作为风场研究中的重要方法,在理论研究及实际飞行验证中都得到广泛应用。然而针对风场估计的研究基本都局限于基于风速矢量三角形关系的解算,而较少研究基于位置信息的风场估计方法。其主要原因是一般研究是基于空速及地速测量相对比较准确这一前提条件,然而根据对实际飞行试验的分析,这些量测信息往往存在一定的误差,从而导致风场估计的精度不高。
针对上述问题,本文提出了一种基于位置信息的小型固定翼无人机多步长风场估计方法,该方法利用无人机飞行环境下的航迹推算(DR)及导航系统(GPS)的定位偏差对风矢量进行了逐步估计,并进一步研究了步长阈值的选取限制,最后利用无人机飞行试验数据详细探讨了步长的不同选取对此方法估计精度的影响。
1多步长风场估计方法描述
无人机飞行位置可以由导航系统测量得到,而通过其当前位置、飞行要求及飞行空速可对下一时刻无人机飞行位置进行推算,并依次推算出整个飞行航迹。但是此推算得到的位置信息与导航定位得到的信息之间存在偏差,此偏差主要来源于风干扰的影响。因此,通过航迹推算方法与导航系统定位可实现对风信息的提取和估计。
假设风在各步长μ内均匀变化,DR推算在各推算时间h内的起始位置均为上一时刻的导航系统定位点,则此推算时间内导航系统测量位置、DR推算位置与风的影响呈矢量三角形关系,如图1所示。

图1 基于飞行位置的风场估计方法
由图1可知,取多个时间步长作为推算时间,在无人机的整个飞行过程中可取多个推算单元,利用导航系统及DR位置可以通过矢量计算求得各时间单元内风的影响,进一步求得此段时间内的平均风速。
步长为μ时,k时刻导航系统测量位置为
(1)k时刻的DR推算位置为
(2)式中,g(k)和J(k)分别为k时刻导航系统的测量位置和DR推算位置,xg(k)、yg(k)和zg(k)为导航系统测量位置在x、y和z三方向的分量,xJ(k)、yJ(k)和zJ(k)为推算位置在x、y和z三方向的分量,Ng(k)和NJ(k)分别为导航系统和DR推算的量测噪声。
取m个步长作为推算时间,即h=mμ,则k+m时刻风速的估计值可以表示为

(3)式中,w(k+m)为k+m时刻风速的估计值,f(g)和f(J)分别为关于导航系统位置矢量和DR推算位置矢量的函数,代入k时刻和k+m时刻的位置信息,(3)式可表示为
(4)DR推算在各推算单元内的起始位置均取为上一时刻的导航系统定位点,则
(5)用k+m时刻的风估计值w(k+m)可对k+m时刻之后时间μ内的风场进行估算,即
(6)由(5)式可应用k时刻位置信息可对k+m时刻飞行航程进行推算,进而对k+m时刻位置进行估计,通过(6)式可对k+m后一个时间单元内的风速进行计算,因此,整个飞行时间内的风速可由此方法分段递推得到。
2推算时间阈值及推算函数
2.1推算时间的阈值限定
为避免发生频率混叠,推算时间h应遵循采样定理:ωs≥2ωc,其中ωs为采样频率,ωc为系统最高频率,由此可限定推算时间的最大阈值;根据导航系统定位原理,当推算时间选取过小,即推算步长数过大时,相邻2次推算时间内导航系统获得地理位置信息含有较大的噪声,利用此数据计算的风速存在较大偏差,因此,推算时间应大于导航系统最低可精确分辨要求。
综上所述,推算时间应选择在一个最佳阈值之内,以使估计风速频谱不产生频率混叠,且导航系统保持较高的定位及测算速度精度。
2.2整/非整步长下推算函数的确定
推算时间h可由时间步长μ及步长数τ联合表示,即h=τμ。步长数的选取可为整数,也可为非整数。

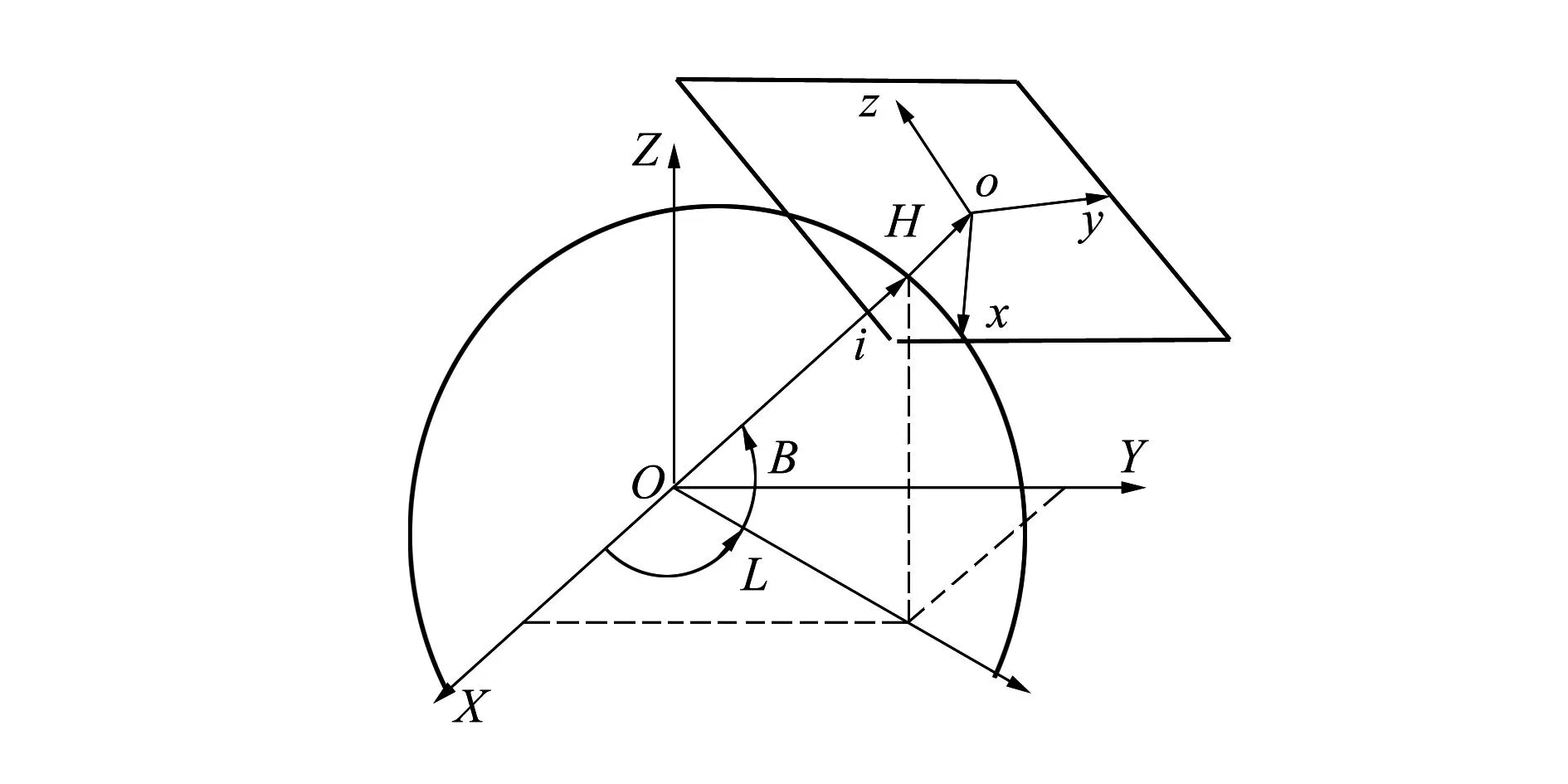
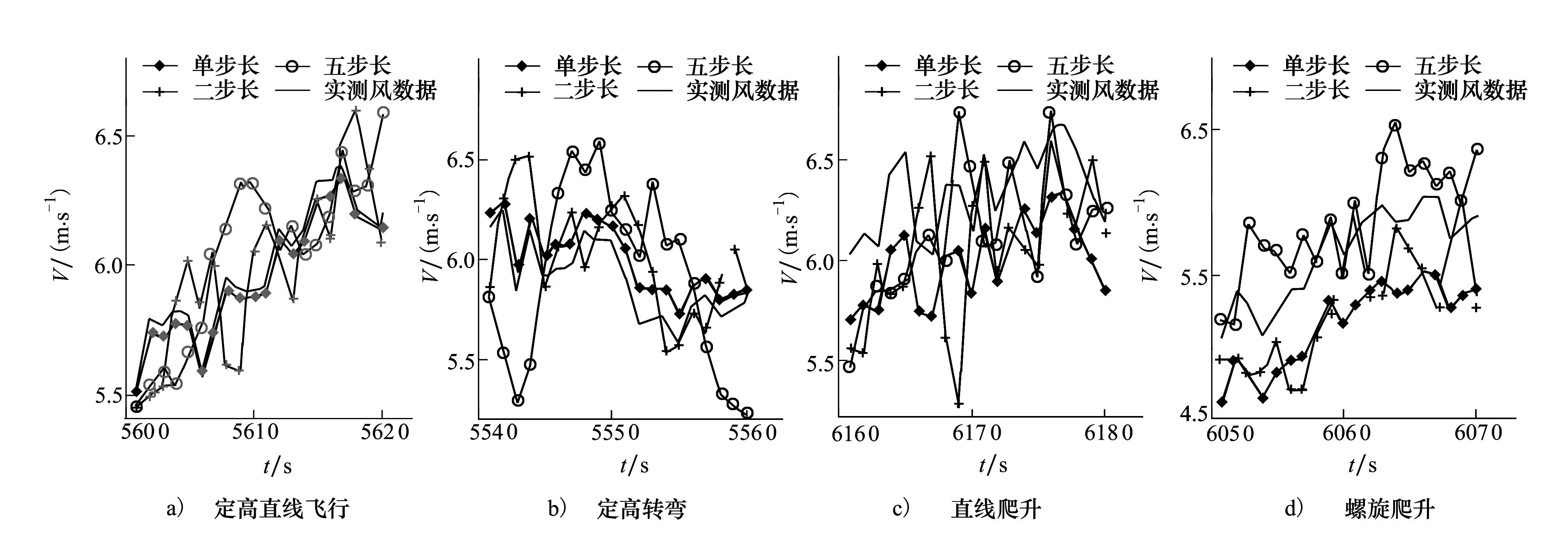
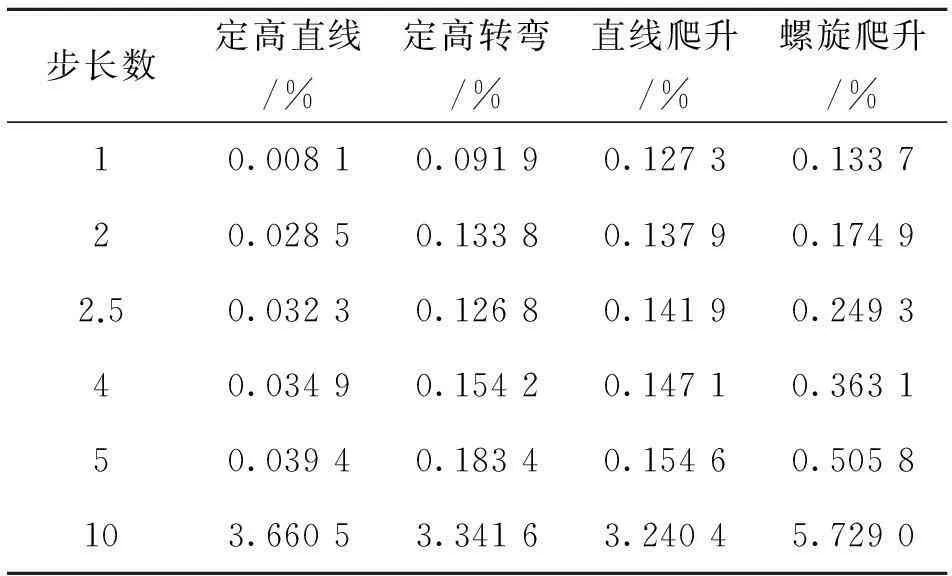
(7)当步长数τ为非整数,即nμ (8)此函数中的系数a0~ak-1可通过h前面的k个时间步长处的函数方程组联合求解为 (9)式中,W(ξ)表示(n-k)μ~nμ中各整数步长下风信息组成的k×1阶矩阵;A为a0~ak-1组成的k×1阶系数矩阵;V表示k×k阶范德蒙矩阵,其具体可表示为 (10) 当取k=2时,(8)式中的多项式外推算法变为简单直线外推,即利用nμ及(n-1)μ处的风信息利用距离直接求解。此时估算耗时最短,但不能反映风场变化趋势,精度较低。 通过(8)式~(10)式得到的非整数步长处的风估计值,可根据耗时及估计精度要求选择合适的项数,当要求估算速度最快时,可选用直线外推;当对估计耗时无严格要求,但需要估算精度较高时,可选用高阶多项式进行求解。 综上,推算时间h处的推算函数可由(7)式或者(10)式求解得到。 3飞行试验数据的预处理 无人机飞行试验数据具有模型估计数据不具备的真实性,是良好的风场估计研究数据源。然而无人机飞行获得的实测数据中通常存在野值、漏测及多测等情况,且测量数据的准确性及可读性都有待考证,因此利用试飞数据前需对其进行预处理。对数据的预处理包括数据读入、剔除野值以及对部分变量的校正和变换。对数据的校正主要为气压高度校正;变换主要为地球大地坐标系到站心地平直角坐标系的转换。 3.1高度测量精度的校验 无人机试飞得到的高度数据正确性及精度不明确,当研究无人机在某高度附近完成运动模态作业时,高度测量的不准确将对试验结果产生影响。为验证高度测量的准确性,利用试飞测得的气压数据对飞行绝对高度进行估算,并与实测高度数据进行比较,从而完成对测量高度数据的验证及校准。 取传感器探测的气压值作为该时刻的气压理论值,应用高度与气压的计算公式解算出此时刻无人机飞行的理论高度H为 (11) 式中,R=8.51为常数;T为热力学温度,与摄氏温标T的转换为T=t+273;g为重力加速度;M=29为气体的分子量;P0=101.325 kPa为标准大气压;P为高度为H处的气压值。 由(11)式求得的理论高度值为对应传感器测量气压的绝对高度值,将其与实测高度进行对比,可验证此实测高度数据的准确性和精度。 3.2坐标系转换 飞行试验数据中的位置信息由经纬度表示,而对风的研究及估计工作均在站心地平直角坐标系下完成,因此,需要对所得试飞数据进行坐标转换。首先将试验数据由地球大地坐标系S-BLH转换到参心空间直角坐标系S-OXYZ,再转换到站心地平直角坐标系S-oxyz,如图2。 图2 地球大地坐标系与站心地平直角坐标系的转换 地球大地坐标系S-BLH到参心空间直角坐标系S-OXYZ的转换关系矩阵为 (12) 参心空间直角坐标系S-XYZ到站心地平直角坐标S-oxyz的转换关系矩阵为 (13) 式中:r为地球半径,B为纬度,L为经度,H为大地高;X、Y和Z分别为参心空间直角坐标系S-OXYZ的坐标值,x、y和z分别为站心地平直角坐标S-oxyz的坐标值。 假设i表示地球大地坐标原点对应的参心空间直角坐标值,j表示参心空间直角坐标系内任意一点的坐标值。则由地球大地坐标系到站心地平直角坐标系的转换关系可以表示为 (14) 4试验结果与分析 4.1试验条件及飞行轨迹 某小型固定翼无人机在某次飞行试验中从地面开始绕方形轨迹回旋上升至5 000m空中,再沿简单飞行轨迹落回地面。此过程中飞行空速约为120~150m/s,时间步长约为μ=1s,飞行模态包含定高直线飞行、定高转弯、直线爬升和螺旋爬升等。 选取飞行高度约为3 600m和4 700m的两段数据对无人机飞行轨迹进行观察和分析,如图3所示。由图可知,在3 600m左右时,无人机在空中完成1次回旋飞行,此过程航迹简单,且包含高直线飞行、定高转弯、直线爬升和螺旋爬升4种运动模态;在4 700m左右,无人机在空中完成1次“8”字型飞行,而后进行1次“U”型转弯,此飞行过程中也包含上述4种运动模态。 由于3 600m和4 700m的飞行轨迹中均包含无人机飞行中的4种主要模态,且包含飞机常见飞行形状,因此选这两高度下的数据进行分析,并应用多步长风场估计方法研究两不同高度下各飞行模态时风速的估计值。 图3 无人机飞行轨迹图 4.2飞行高度解算及校验 将(11)式解算出的高度与无人机飞行试验得到的实测高度进行对比,如图4所示。由图可知,解算高度与实测高度之间偏差很小,在飞行开始后约2.5h两者间的偏差达到最大,约为50m,而随着无人机飞行高度逐渐增加,误差将逐渐越小,并最终保持在10m之内。由此可认为无人机飞行试验得到的高度数据具有较高的准确性,且测量精度满足研究分析需求。 图4 解算高度与探空高度对比图 为增加数据可靠性,取实测高度及解算高度的平均值作为高度输入值进行风场估计方法的仿真和验证分析。 4.3风场估计试验 情况13 600m高度下的多步长风场估计为验证多步长风场估计方法的正确性,并分析步长数对估计精度的影响,以无人机飞行在3 600m高度时的风速测量曲线作为风速理论值,分别在定高直线飞行、定高转弯、直线爬升和螺旋爬升4种运动模态下对飞行风场进行估计。选取步长数分别为1、2和5的估风曲线与风速理论曲线进行对比,如图5所示。 图5 3 600 m高度时4种飞行模态下基于单步长、二步长、五步长的风速估计曲线与理论曲线的对比 仿真中曲线分别代表基于单步长、二步长、五步长的风速估计曲线和飞行试验测量风曲线。由仿真可知,单步长下的风速估计曲线与试验测量风速曲线的走势和波动情况最为相似,但大都存在一定偏差;随着步长的增大,在二步长下,估计风速逐渐趋近于试验测量值;当采用五步长时,估计曲线产生一个包含实际测量值的包络范围,但由于此时曲线波动较大,估计风速与实际测量值间的误差将增大。由仿真还可以看出,不同飞行模态下估计风速的误差大小不同,飞行在固定高度平面时的估计误差大都比爬升模态下的估计误差小,估计精度高。 情况24 700m高度下的多步长风场估计取无人机飞行在4 700m高度时的风速测量曲线作为理论值,分别在定高直线飞行、定高转弯、直线爬升和螺旋爬升四种运动模态下与步长数分别为1、2和5的风场估计曲线进行对比,如图6所示。 图6 4 700 m高度时4种飞行模态下基于单步长、二步长、五步长的风速估计曲线与理论曲线的对比 仿真中曲线分别代表基于单步长、二步长、五步长的风速估计曲线和飞行试验测量风速曲线。由仿真可知,单步长下的风速估计曲线与实际测量风速曲线的走势和波动情况最为相似,但大都存在一定偏差;随着步长的增大,在二步长下,估计风速逐渐趋近于试验测量值;当采用五步长时,估计曲线产生一个包含实际测量值的阈值范围,但由于此时曲线波动较大,估计风速与试验测量值间的误差将增大。由仿真还可以看出,不同飞行模态下估计风速的误差大小不同,飞机作直线飞行时的风估计误差大都比飞机转弯时的估计误差小,估计精度高。 4.4试验对比及分析 对仿真结果进行量化分析,对比各步长下估计风速及真实风速之间的均方误差,可得在3 600m下步长数分别为1、2、2.5、4、5、和10h多步长方法估计误差如表1;在4 700m下步长数分别为1、2、2.5、4、5、和10h多步长方法估计误差如表2所示。 表1 3 600 m下多步长风场估计方法相对误差对比 表2 4 700 m下多步长风场估计方法相对误差对比 由表1和表2可以看出,此风场估计方法适用于步长数为整数和非整数两种类型。当步长数取为2.5时,此风场估计方法估算精度处于步长数为2和4的风场估计精度之间,证明选取非整数步长数时,多步长风场估计方法的估算精度无明显下降。 分别对比表1和表2中各步长下相对误差可以得出以下结论:选取步长数为1~10时,风速估计值与飞行测量值之间的相对误差大部分不超过10%,估计效果较好;步长数选为1~5时,估计误差较小,大多不超过1%;当步长数选取过大时,估计误差将大幅度增加,达到5%~10%。由两表中还可得出:相同高度时,直线飞行估计风速大多比转弯飞行估计风速精度高,定高飞行估计风速大多比爬升飞行时估计风速精度高。 通过表1和表2之间对比可以看出,表2估计风速相对误差大部分高于表1,结合图3飞行在3 600 m和4 700 m下的轨迹,可得出:飞行轨迹复杂程度对风场估计精度也存在影响,且高度越高,飞行轨迹越复杂,风场估计精度越低。 5结论 本文提出了基于位置信息的小型固定翼无人机多步长风场估计方法,并利用飞行试验数据对不同步长下的风场估计精度进行比较,从而选取步长的最佳阈值。 此研究工作基于无人机试飞数据,验证了多步长下无人机风场估计方法的准确性;同时定量分析了此方法的估算精度,选取高精度的步长数范围,为无人机探测风场的研究提供了一种新的研究思路。 参考文献: [1]Chi C Y, Li F K. A Comparative Study of Several Wind Estimation Algorithms Forspaceborne Scatterometers[J]. IEEE Trans on Geoscience and Remote Sensing, 1988, 26(2):115-121 [2]阎启, 谢强, 李杰. 风场长期观测与数据分析[J]. 建筑科学与工程学报, 2009, 26(1): 37-42 Yan Qi, Xie Qiang, Li Jie. Long-Term Observation and Data Analysis of Wind Field[J]. Journal of Architecture and Civil Engineering, 2009, 26(1): 37-42 (in Chinese) [3]Brian R T. A Full-Envelope Air Data Calibration and Three-Dimensional Wind Estimation Method Using Global Output-Error Optimization and Flight-Test Techniques[C]//AIAA Atmospheric Flight Mechanics Conference, 2012: 1-16 [4]欧雷. 大气数据测量不确定度评定[J]. 计测技术, 2007, 27: 85-87 Ou Lei. Metrical Uncertainty Evaluation of the Atmospheric Data[J]. Metrology & Measurement Technology, 2007, 27:85-87 (in Chinese) [5]Nelson G G. Real Time Winds Data Flight Management[C]//28th Aerospace Sciences Meeting, 1990: 565-571 [6]Qu Y H, Zhang Y T, Zhang Y M. Optimal Flight Path Planning for UAVs in 3-D Threat Environment[C]//2014 International Conference on Unmanned Aircraft Systems (ICUAS), 2014:149-155 [7]周伟静, 沈怀荣. 一种基于小型无人机的风场测量方法[J]. 测试技术学报, 2009, 23(4): 297-302 Zhou Weijing, Shen Huairong. A Wind Measuring Method Based on a Mini-UAV[J]. Journal of Test and Measurement Technology, 2009, 23(4):297-302 (in Chinese) [8]Qu Y H, Feng L. A Method of Wind Field Estimation and Trajectory Correction Online in DR/GPS/RP Integrated Navigation of UAV[C]//IEEE International Conference on Automation and Logistics, 2008: 1402-1407 [9]武涛, 夏群利, 刘大卫,等. 基于大气测量信息的风估计算法研究[J]. 北京理工大学学报, 2011, 31(4):420-424 Wu Tao, Xia Qunli, Liu Dawei, et al. Study of the Method of Wind Estimate Based on Measuring Air Data[J]. Transactions of Beijing Institute of Technology, 2011, 31(4): 420-424 (in Chinese) [10] Morelli E A, Klein V. Accuracy of Aerodynamic Model Parameters Estimated from Flight Test Data[J]. Journal of Guidance, Control and Dynamics, 1997, 20(1): 74-80 US News and World Report把北大、清华、复旦、浙江、中国科技、 上海交通、南京、中山、武汉、华中科技十校 列入2016年世界高校最强的前265名 中国日报Thursday,Cotober 8th,2015刊载了US News and World Report 2014年开始列出world′s top 750 universities overall的名次。中国十高校列入2016年世界最强高校的前265名:北京大学41名,清华大学59名,复旦大学96名,浙江大学105名,中国科技大学130名,上海交通大学136名,南京大学180名,中山大学198名,武汉大学251名,华中科技大学265名。 胡沛泉 2015年10月 Multi-Step Wind Field Estimation Online of Small Fixed-Wing UAVs Qu Yaohong, Yu Lili, Zhou Ying, Yuan Dongli (Department of Automatic Control, Northwestern Polytechnical University, Xi′an 710072, China) Abstract:Based on the vector relationship of motion locations on small fixed wing UAV, a multi-step wind field estimation method is proposed. And the impact of steps on estimation accuracy is tested with flight data. First, the estimation model which is based on GPS/DR is obtained with the location information of UAV. Next, the optimal value of steps is obtained with testing flight in four different models. In the simulation, under the condition of 150m/s speed, 1 second sample step and no more than 5 steps, the wind information is estimated accurately with the proposed method and the measurement error of wind speed does not exceed 10%. Key words:computer simulation, errors, estimation, experiments, fixed wings, flight dynamics, global positioning system, matrix algebra, measurement errors, optimization, trajectories, unmanned aerial vehicles (UAV), vectors, flight position, flight test, GPS/DR, step, wind field estimation 中图分类号:V19 文献标志码:A 文章编号:1000-2758(2015)05-0750-07 作者简介:屈耀红(1971—),西北工业大学副教授,主要从事无人机风场估计与空中加油技术研究。 基金项目:国家自然科学基金(61473229、60974146)资助 收稿日期:2015-03-31