大型滚塑成型设备支承托轮接触疲劳有限元分析

周建忠，朱 涛，黄 舒，蒋 萍，薛 远，王江明，陈 亮

(1.江苏大学机械工程学院，江苏镇江 212013;2.无锡新开河储罐有限公司，江苏无锡 214154)

滚塑工艺也叫旋转成型工艺，是一种采用旋转加热的方式得到中空塑料制品的工艺技术，与注塑、吹塑等塑料成型工艺相比，其具有设备投资少、模具成本低、产品设计灵活和形式多样等优势，已成为成型大型中空制品不可替代的工艺技术［1］.目前，国内的滚塑成型设备大多停留在对国外现有机型的简单仿制阶段［2］，形式比较单一，大多采用托轮-滚圈进行传动，托轮不仅通过摩擦力带动滚圈与筒体运转，还承载着整个旋转部分的全部重量.设备在实际运转过程中，由于安装精度不够和基础沉陷等原因，各支承结构的回转中心不在一直线上，造成托轮受力不均，而受力不均不仅会加剧磨损，更易使托轮过早地破坏失效.托轮的破坏形式主要有2种:①点蚀、掉渣和鳞状裂纹等形式的表面破坏［3］;②轮辐或轴孔开裂、轮轴断裂等形式的轮体破坏［4］.托轮的造价很高，一旦发生破损失效，会给企业带来巨大的维修与误工费用损失.

托轮-滚圈接触应力计算的传统方法是运用Hertz接触理论与图解法推导出的经验公式［5］，但这种方法计算精度不高且局限性较大.近年来，随着有限元技术的发展，针对托轮-滚圈模型非线性接触应力有限元模拟已有相关研究［3，5-6］，但均未涉及疲劳寿命有限元分析，笔者基于联合仿真技术，运用ANSYS APDL，ADAMS和Fe-Safe软件，进行托轮疲劳寿命估计，找到其危险易损区域，在此基础上，进一步分析危险区域过渡圆角尺寸大小对疲劳寿命的影响.

1 接触应力有限元分析

1.1 有限元模型建立与网格划分

某企业250 m3钢塑复合储罐滚塑成型设备如图1所示.

图1 滚塑成型设备筒体及其支承构件

所用的滚圈-托轮尺寸:滚圈外径为3 220 mm，内径为2 862 mm，宽度为460 mm;托轮外径为830 mm，轴径为210 mm;6块辐板间开有辐孔，孔径为120 mm，宽度与滚圈宽度相等.建模时，笛卡尔坐标系原点取在滚圈的几何中心位置，各坐标轴的正方向规定如下:面向滚圈向右为x轴正方向;重力加速度方向为y轴正方向;滚圈轴线向内为z轴正方向.

为了提高计算精度，选用含有高阶3维20节点六面体固体结构单元SOLID 186进行滚圈-托轮有限元建模.该单元具有任意的空间各向异性和2次位移模式，支持塑性，超弹性，大变形，大应变等混合模式模拟，适用于滚圈-托轮接触模拟.在接触有限元分析中，需要定义材料常数，托轮、滚圈所用材料特性如表1所示.

表1 滚圈托轮材料特性

滚圈采用SWEEP方式进行网格划分;托轮采用四边形网格自由划分，单元尺寸设置为5级智能网格.划分后得到272 948个单元(Element)、4 445 444个节点(Node).托轮与滚圈的接触属于面与面的接触，属于一种高度非线性行为.分析中选取托轮外表面为目标面，采用TARGE170接触单元;滚圈外表面为接触面，采用CONTA174接触单元;摩擦系数为0.15，接触面行为设为Bonded(绑定)，至此2对接触对创建完毕.建立的托轮-滚圈有限元模型如图2所示.

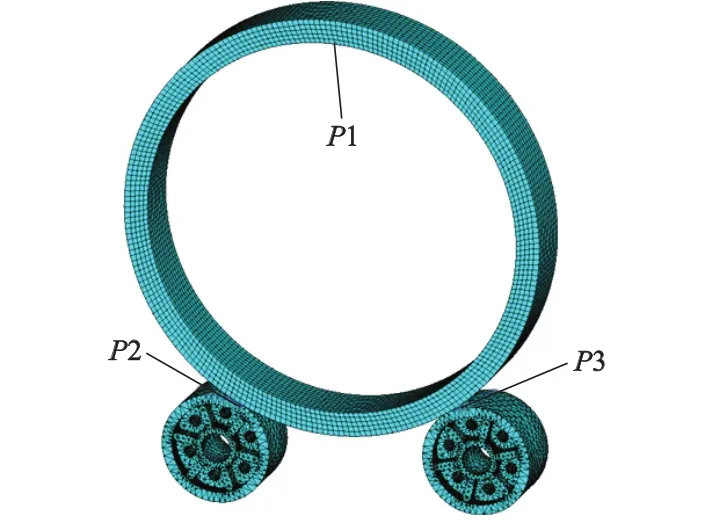
图2 托轮-滚圈有限元接触模型

1.2 网格无关性验证

网格的疏密程度对模拟结果具有一定的影响，为了保证模拟结果的准确率，需要确定计算所用的网格数量与计算结果之间具有无关联性，即网格无关性验证.主要研究托轮-滚圈模型的应力分布，因此，可以在模型上选取3个点的应力来进行网格无关性验证.取滚圈内圈侧面的最高点为P1，左、右托轮侧面与滚圈接触点为P2，P3.这3点相对应的坐标值分别为(0，1 431，-230)，(-805，1 394，-230)，(805，1 394，-230)，具体位置如图 2 所示.按网格由疏到密，依次对模型进行划分.划分后网格数量分别为272 948，554 569，989 955，1 977 739 个.

仿真结果如图3所示，当网格数量从27.3万个变至197.8万个时，随着数量的增加，3点对应的应力值均变化很小，说明在该范围内，网格数量对计算结果的影响很小，可认为27.3万个的网格已达到网格无关，因此取27.3万个的网格作为计算网格.

图3 网格无关性验证结果图

1.3 边界条件与载荷加载

滚圈与托轮的接触属于经典的Hertz接触，该接触不仅传递着整个主回转体的旋转力矩，还承受着来自滚圈内壁的压力及自重［6］.主回转体对滚圈内壁的压力以余弦形式分布，如图4所示.

图4 滚圈余弦压力分布示意图

滚圈内壁的余弦压力分布表达式［7］为

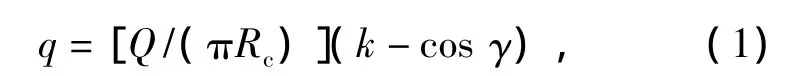
式中:q为滚圈内壁周线上的均布线载荷，N·m-1;Q为垂直方向的载荷，N;Rc为滚圈内外半径的平均值，m;γ 为压力分布角，取值范围为(β，180°)，β=54°;k为常系数.

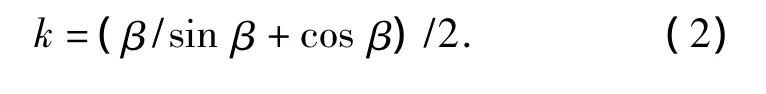
在笛卡尔坐标系中，将cos γ转换为坐标公式:

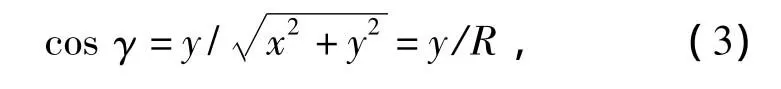
式中R为滚圈内圈半径.

将式(3)代入式(1)得

托轮紧套在托轮轴上，托轮轴可视为刚性轴，因此需对托轮内圈施加全约束［8］;为了避免滚圈发生轴向滑移，约束滚圈一侧面的轴向平移自由度［9］;由于Solid186单元只有平移自由度，缺乏转动自由度，将节点坐标系由笛卡尔坐标系变为圆柱坐标系，在圆柱坐标系下，约束滚圈内壁径向自由度，仅保持其z向转动自由度.对滚圈施加载荷为绕z轴的力矩，数值为25 050 N·m;筒体与物料的总质量m=42 t，采用2组托轮-滚圈支承件进行传动，则滚圈垂直方向载荷Q=mg/2=205.8 kN;利用ANSYS中具有的函数编辑功能定义线性载荷q，然后将其施加到滚圈内表面，即可对滚圈与托轮进行接触应力有限元数值计算.

1.4 有限元计算结果与分析

托轮-滚圈的接触应力分布如图5所示，滚圈等效应力分布如图6所示，滚圈最大应力发生在与托轮接触处，为79.9 MPa，而接触位置的相邻区域应力相对较小，越靠近接触点处应力就越大，可见滚圈与托轮间的接触处存在较大的挤压和磨损.

图5 托轮-滚圈接触应力分布图

图6 滚圈等效应力分布图

滚圈外圈中截面周向等效应力分布曲线如图7所示，滚圈回转1周，外表面的等效应力均经历5次脉冲循环，峰值分别位于滚圈最高处(0°)、水平位置(90°，270°)、与托轮接触处(150°，210°).周期性脉冲应力易使滚圈强度薄弱处和表面缺陷处萌生疲劳裂纹.裂纹扩展导致托轮发生点蚀、掉渣和鳞状裂纹等表面破坏.因此在设计时，应保证滚圈具有足够的强度、刚度和表面硬度，限制变形量，以免过早发生破坏.

图7 滚圈外圈中截面周向等效应力分布曲线

左、右托轮等效综合应力分布如图8所示，不论左托轮还是右托轮，最大等效应力均位于轮辐与轮缘连接处，分别达到104.0，105.0 MPa，说明该处有应力集中现象，实际生产中，托轮的轮体破坏也多数于此处萌生裂纹.因此，该型托轮的结构有待改进，可以采用适当增加轮辐与轮缘过渡圆角半径或开卸载槽等方法，以减少应力集中.

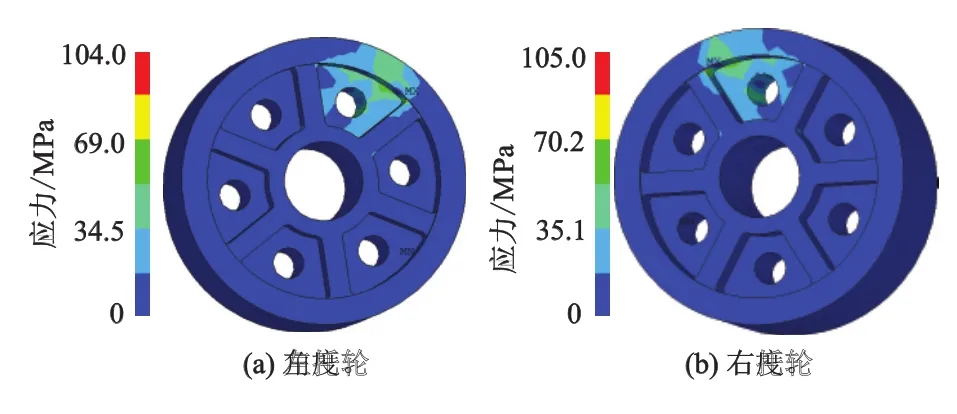
图8 左、右托轮等效应力分布图

左、右托轮中截面外圈周向等效应力分布对比曲线如图9所示.

图9 左、右托轮中截面外圈周向等效应力分布对比曲线

托轮外圈等效应力呈对称分布，与滚圈接触处等效应力最大，远离托轮接触处等效应力逐渐减低，对面处达到最低.此外，左、右托轮沿周向等效应力分布趋势非常接近，最大差距仅9 MPa，说明左、右托轮受力均匀，未发生明显的载荷偏置现象.差距的出现主要是模型装配误差引起的.在实际生产过程中，可以通过控制托轮-滚圈安装工艺避免因安装误差引起左右托轮受力不均.

2 疲劳寿命分析

2.1 材料p-S-N曲线

材料的p-S-N曲线是进行疲劳可靠性分析与寿命估计的依据，反映了在不同存活率p下，材料的疲劳寿命N与应力幅值S的关系，其通用式为

式中:Np为存活率为p时材料的循环破坏次数;σ为应力平均值;ap，bp为常数，与选取的存活率有关.

根据文献［10］查得，托轮所选用的材料，在存活率p为99%时，ap=21.249 1，bp=-6.812 8;将数值代入式(5)，使用Origin软件绘出的曲线如图10所示.提取托轮材料的不同循环次数下的应力值，将其对应输入到Fe-Safe软件中的FatigueS-NTable，完成材料的疲劳特性模型的建立.

图10 托轮材料失效概率为1%的S-N曲线

2.2 载荷谱

将建立好的托轮-滚圈接触模型导入到ADAMS仿真软件中，然后对模型添加质量属性、约束副、驱动与载荷，完成从3维模型到虚拟样机的转换.滚圈、托轮Ⅰ、托轮Ⅱ分别与大地施加旋转副(revolute joint)，并在托轮的旋转副上施加旋转运动激励，使其保持等速旋转.滚圈与托轮之间施加实体-实体碰撞接触力(solid to solid contact);滚圈上施加阻力力矩.取从动轮阻力矩为25 050 N·m，托轮转速为35 r·min-1，托轮-滚圈之间的静摩擦系数为0.15，动摩擦系数为0.10，设置重力场gravity方向为y向，计算时长为0.8 s，仿真步数为200，设置完成后，进行求解.通过动力学分析得到托轮-滚圈之间接触力随时间的历程曲线如图11所示，接触力在1个均值载荷132 kN附近以一定的幅值上下波动.

图11 托轮-滚圈接触力时间历程曲线

通过上述动力学仿真分析，得到了托轮所受载荷的时间历程信息，将结果以DAC数据格式输入到疲劳仿真软件，进而获得了托轮疲劳寿命分析所用的载荷谱数据.

2.3 疲劳寿命计算结果

在高级疲劳耐久性分析软件Fe-Safe中，基于简化的弹塑性假设和Miner累积疲劳求和法则，利用ANSYS APDL计算的应力结果和ADAMS载荷时间历程，对托轮进行疲劳寿命仿真分析.计算结果需通过ANSYS APDL后处理器POST1查看，读取的疲劳寿命结果如图12所示.

图12 托轮的疲劳寿命云图

从图12可以看出:托轮的易损薄弱区域主要位于轮辐与轮缘的交接处和托轮外圈;前者属于轮体破坏区域，后者属于表面破坏区域;疲劳寿命最低值为104.596次，对应的节点位于轮辐与轮缘的过渡区域，说明轮体破坏是托轮失效的主因.

2.4 过渡圆角尺寸对托轮疲劳寿命的影响

模拟发现，托轮的最大应力位于应力集中处，而应力集中会产生局部高应力，引起脆性材料断裂，使物体产生疲劳裂纹.为了减轻应力集中对疲劳强度的影响，避免托轮在正常工作时发生疲劳断裂，在进行结构设计时就必须注意受力轮辐与轮缘过渡部位.为了研究轮辐与轮缘过渡圆角尺寸对托轮的疲劳寿命影响，采用圆角半径分别为 10，15，20，25，30 mm的托轮进行有限元分析.分析结果如图13所示.

图13 不同过渡圆角半径下的托轮疲劳寿命云图

从图13可以看出:5种圆角半径R不同的托轮，疲劳寿命薄弱点均出现在轮辐与轮缘交接处，此处应力集中系数最大，也最易损坏.说明了应力集中是托轮的主要疲劳源，在长期的变化载荷作用下，应力集中处会最易产生断裂破坏.托轮疲劳寿命随圆角半径变化曲线如图14所示，过渡圆角R从10 mm增加到15 mm时，疲劳寿命从104.452次增加到104.596次，提高约39.32%;R从15 mm增加到20 mm时疲劳寿命从104.596次增加到104.937次，提高约119.28%;R从20 mm增加到25 mm时，疲劳寿命从104.937次增加到105.333次，提高约148.89%;R从25 mm增加到30 mm时，疲劳寿命从105.333次下降到105.237次时，降低约24.74%.

图14 托轮疲劳寿命随圆角半径变化曲线图

结果表明:增加轮辐与轮缘交接处过渡圆角尺寸，可以降低局部高应力，削弱应力集中现象，显著提高构件寿命;但是，过渡圆角过大时，构件的强度会降低，疲劳寿命有所下降.因此，对于φ830 mm的托轮设计，过渡圆角选用R=25 mm，疲劳寿命值最佳.此外，还可在圆角表面处进行滚压、喷丸和电解抛光等处理提高表面强度，进而延长托轮的旋转弯曲疲劳寿命极限.

3 结论

1)托轮外圈接触应力呈对称分布，与滚圈接触处等效应力最大，远离托轮接触处等效应力逐渐减低，对面处达到最低.

2)左、右托轮沿周向等效应力分布趋势非常接近，最大差距仅9 MPa，说明左、右托轮受力均匀，载荷偏置现象极小.

3)托轮的危险点位于轮辐与轮缘的交接处，此处由于应力集中产生了局部的高应力，在长期的循环变载荷作用下，最容易损坏.

4)随着轮辐与轮缘的交接处过渡圆角半径增加，托轮的应力集中现象减弱，疲劳寿命得到显著提高，但圆角半径过大时，构件的强度降低，寿命会下降.模拟发现，对于φ830 mm的托轮，过渡圆角选用R=25 mm，疲劳寿命值最佳.

References)

［1］张 凯，夏 天.滚塑成型技术的研究现状及其展望［J］.机械制造与自动化，2013，41(1):52-54.

Zhang Kai，Xia Tian.Research status and prospect of rotational moulding technique application［J］.Machine Building and Automation，2013，41(1):52-54.(in Chinese)

［2］彭 威，关昌峰，秦 柳，等.滚塑机烘箱内部温度场的数值模拟研究［J］.机械设计与制造，2012(9):105-107.

Peng Wei，Guan Changfeng，Qin Liu，et al.Numerical simulation study on temperature field in an oven of rotational molding machine［J］.Machinery Design＆Manufacture，2012(9):105-107.(in Chinese)

［3］赵先琼，刘义伦，周 贤.回转窑托轮力学行为的有限元分析［J］.湖南大学学报:自然科学版，2002，29(6):52-56.

Zhao Xianqiong，Liu Yilun，Zhou Xian.Finite element analysis of mechanical conditions for supporter of rotary kiln［J］.Journal of Hunan University:Natural Sciences Edition，2002，29(6):52-56.(in Chinese)

［4］王和慧，程 静，周金水，等.大型回转窑支承系统的力学行为分析［J］. 机械强度，2012，34(1):77-85.

Wang Hehui，Chen Jing，Zhou Jinshui，et al.Analysis of the mechanical behavior of the supporting system of a large rotary kiln［J］.Journal of Mechanical Strength，2012，34(1):77-85.(in Chinese)

［5］Li Xuejun，Jiang Lingli，Liu Deshun，et al.Research on supporting load distribution of large-scale rotary kiln with multi-support and variable-stiffnes［J］.Chinese Journal of Computational Mechanics，2005，22(2):207-213.

［6］Shen Yiping，Wang Songlai，Li Xuejun，et al.Multiaxial fatigue life prediction of kiln roller underaxis line deflection ［J］.Applied Mathematics and Mechanics:English Edition，2010，31(2):205-214.

［7］李学军，肖友刚，王梅松，等.回转窑托轮对轮带最佳支承角的有限元优化［J］.矿冶工程，2003，23(4):48-50.

Li Xuejun，Xiao Yougang，Wang Meisong，et al.Optimum supporting angles of kiln wheel to kiln tyre a FEM optimization［J］.Mining and Metallurgical Engineering，2003，23(4):48-50.(in Chinese)

［8］del Coz Diaza J J，Rodriguez Mazon F，Garcia Nieto P J.Design and finite element analysis of a wet cycle cement rotary kiln［J］.Finite Elements in Analysis and Design，2002，39:17-42.

［9］Pazand K，Sharial Panahi M，Pourabdoli M.Simulating the mechanical behavior of a rotary kiln using artificial neural networks［J］.Materials and Design，2009，10(9):3468-3473.

［10］机械工程材料性能数据手册编委会.机械工程材料性能数据手册［M］.北京:机械工业出版社，1994.