磁通切换型永磁电机非线性磁网络分析

张 淦 花 为 程 明 王宝安

（东南大学电气工程学院 南京 210096）

1 引言

随着能源危机的不断加剧，采用永磁励磁取代电励磁以节省能源消耗已成为全世界的共识。特别是目前广泛研究的新能源汽车，要求电机驱动系统体积小、重量轻、效率高、可靠性强、转矩出力大、调速范围宽[1]。现代永磁电机的发展已经超过20年，目前根据永磁体安放位置可分为转子永磁式和定子永磁式两大类[2]。对于目前应用最为广泛的表面贴装式结构而言，为了固定磁钢通常需要采取特定的措施，增加了制造成本。此外，转子永磁式电机不利于冷却，也成为限制其应用的一个重要原因。针对上述问题，出现了定子永磁式的新型永磁无刷电机，包括三种代表结构：双凸极永磁电机（Doubly-Salient Permanent Magnet Machine，DSPM 电机）[3,4]、磁通切换型永磁电机（Flux-Switching Permanent Magnetic Machine，FSPM 电机）[5-7]、磁通反向型永磁电机（Flux-Reversal Permanent Magnet Machine，FRPM 电机）[8]。现有文献表明，这三种电机中又以FSPM 电机的转矩输出能力和功率密度最为优越[9]。

FSPM 电机作为一种新型定子永磁型双凸极无刷电机，其定子上装配有永磁体和集中式电枢绕组，转子结构极为简单。同时，由于FSPM 电机具有绕组一致性和绕组互补性[10]，可以减少永磁磁链和反电动势波形中的高次谐波分量，保证了该电机即使在采用集中绕组和直槽转子的条件下，仍可以获得较高正弦度的永磁磁链与空载感应电动势[9,10]，较适合无刷交流运行场合，可以适用多种控制策略[2]，如针对传统电机的SVPWM 控制及直接转矩控制[11-13]。此外，FSPM 电机具有聚磁效应，使得气隙磁通密度可以设计得很大（最高可达2.2T），导致其在定子外径相同的条件下，转矩和功率都可以高于其它两种定子永磁型电机。而且，由于FSPM 电机中永磁磁场和电枢反应磁场从磁路而言为并联关系，使得永磁体具有很强的抗退磁能力，提高了电机的运行可靠性。以上优点使FSPM 电机其非常适合于对电机尺寸有严格限制，同时又需要较高出力及较高可靠性的场合，例如航空、航天、航海和电动汽车等领域。

另一方面，目前电机分析与计算方法中，有限元法（Finite Element Analysis,FEA）被广泛用于对电机进行精确电磁性能计算，尤其适用于非线性强饱和情况。现有的基于有限元法的商用软件功能强大，非常成熟，如ANSYS、ANSOFT 和FLUX 等。虽然有限元法可以准确计算电机静态特性，但是这种方法较为复杂，需用较长的计算时间，尤其在电机初始设计阶段，需要多次计算各种不同结构参数下的电机静态特性。此时使用有限元法则显得十分不便，计算成本昂贵。而等效磁路法一直是电机工程中常用的磁场近似计算方法，该方法可以方便、迅速地求得电机的磁场分布和参数，并且可以加深对电机结构的理解，在满足精度要求时，在电机的初始设计阶段具有很大的优势。文献[14]中提出了一种针对DSPM 电机的磁网络模型，并分析了考虑局部饱和效应后如何对初始模型进行完善。文献[15]中提出了一种针对FSPM 电机的集中参数磁路模型，但是对电枢电感的计算同有限元法相比，仍存在较大偏差。

因此，本文基于一台三相定子12 槽/转子10 极的FSPM 电机，提出了一种非线性磁网络模型。该模型可以充分考虑电机铁心内部磁场饱和的影响，对电机的电磁性能进行计算，例如气隙磁通密度分布、电枢线圈永磁磁通和感应电动势等。然后，基于此原始模型，在考虑局部饱和影响后对模型进行了修改，本文称修改后的模型为初始模型。进一步地，为了提高磁网络分析的精度，在初始模型基础之上又提出了多段永磁支路模型和导磁桥模型。需要说明的是，这两种新模型均考虑了局部饱和效应的影响，而相比较于初始模型，两种新模型对电机电磁性能的分析，尤其是电感的计算更为精确。通过与有限元分析数据的比较，结果表明上述四种磁网络模型中，导磁桥模型具有最高的计算精度。最后，通过一台样机，验证了有限元分析及磁网络模型的正确性。

2 FSPM 电机结构

图1 所示为一台三相定子12 槽/转子10 极的FSPM 电机。以本图中电机为例，其电机定子铁心由12 块U 形导磁单元组成，相邻的两块U 形单元中间嵌有一块永磁体，因此，共有12 块交替切向充磁的永磁体。此外，三相对称分布的集中式电枢绕组线圈套在由两个U 形单元与一块永磁体所组成的定子导磁齿上。详细的电机结构分析可见参考文献[9]，电机的具体参数见表。

图1 定子12 极/转子10 极FSPM 电机结构示意图Fig.1 12-stator-pole/10-rotor-pole FSPM machine

FSPM 电机在一个机械周期（36°，对应的电周期为360°）内有两个典型的转子位置，即：θr=0°，对应A 相绕组匝链的永磁磁通为零；θr=9°，对应A相绕组匝链的永磁磁通为峰值，其中θr为转子位置的机械角度。图2 所示分别为在这两个特殊转子位置时的开路永磁磁场分布，图3 所示为单独在A 相电枢绕组中加载8A/mm2电流密度时（槽满率kpf=0.75）的合成磁场分布，其相应的磁通密度分布如图4 和图5 所示。需要说明的是，本文在分析加载A 相电枢电流的各电磁特性时，选取的上述电流密度（即8A/mm2）相对较大，主要有以下三个原因：①选取较大的电枢电流，可以通过有限元分析更清晰的观察及说明电枢反应的效果；②电流密度较小时的电枢反应较微弱，较难比较本文中所提出的几种不同的磁网络模型在分析电感特性时的差别；③考虑到电机过载运行工况或采用水冷时，电枢中可能通入较大的电流值。

表 磁通切换电机设计参数Tab.Specification of the FSPM machine

图2 开路磁场分布Fig.2 Open-circuit field distributions

图3 A 相电枢绕组加载8A/mm2 电流密度时的磁场分布，槽满率为kpf=0.75Fig.3 Field distributions when phase A loaded with a current density of 8A/mm2,slot pakage factor kpf=0.75

图4 开路磁通密度分布Fig.4 Open-circuit flux density distributions

图5 A 相电枢绕组加载8A/mm2 电流密度时的磁通密度分布，槽满率kpf=0.75Fig.5 Flux density distributions when phase A loaded with current density of 8A/mm2,slot pakage factor kpf=0.75

3 非线性磁网络模型的建立

3.1 磁网络原始模型的建立

对于本文中的定子12 槽/转子10 极FSPM 电机而言，由于具有较多的定转子槽数与齿数，所以选择在直角坐标系下对磁网络进行建模。

首先，磁网络模型中的每条支路磁通均满足

式中 Φ,G 和F——所在支路的磁通、磁导和磁动势（Magneto-Motive-Force，MMF），而支路磁导G 可由式（2）计算得到

式中 μ0——真空中的磁导率；

μr，S，l——其所在支路对应的电机材料相对磁导率、磁通匝链方向截面积和磁通流通方向长度。

需要指出，μr数值取决于其所在支路的磁场饱和程度，并非常数，需通过迭代查找相应的B-H 曲线得到。

在FSPM 电机中，由于永磁体和电枢电流二者产生的磁通方向相互平行，而永磁体中的磁通密度变化不明显，所以一块永磁体的磁动势和磁导可以分别由式（3）和式（4）计算得到

式中 Fm——等效永磁磁动势；

Gm——永磁体所在支路磁导；

hm——永磁体磁化方向厚度；

lm——永磁体宽度；

Br——永磁体剩磁。

定子槽中电枢绕组产生的磁动势可由式（5）计算得到[15]

式中 Nc——单个定子槽中的电枢线圈匝数；

I1和I2——流入和流出定子槽的电枢电流大小（针

对双层绕组）。

经上述分析，可得到FSPM 电机硅钢片和永磁体部分的等效磁路，相应支路磁导及磁动势的计算方法可以参照式（1）～式（4）。然而，对于这类双凸极结构电机而言，最难部分在于定转子齿槽间气隙的构成随转子位置变化而改变。因此，气隙磁路所对应的气隙磁导的确定方法较复杂。图6 为定转子间部分气隙的等效磁路构成示意图，其气隙磁导可分为图7 所示的五种典型种类，其相应计算方法见对应公式。在得到不同转子位置的气隙磁路构成后，即可得到FSPM 电机的完整磁网络模型。由此可见，该FSPM 电机的磁网络模型是一个随转子位置变化的变网络非线性磁路模型。如图8 所示，为转子位置在θr=0°时的磁网络原始模型。

图6 气隙磁路简化示意图Fig.6 Simplified flux paths in air-gap region

图7 典型的气隙磁导Fig.7 Typical air-gap permeances

图8 FSPM 电机原始磁网络模型，θr=0°Fig.8 The original magnetic network model of the FSPM machine,θr=0°

3.2 磁网络初始模型的建立

图9 所示为，当定子U 形铁心单元的一个导磁齿与转子齿部分重合时，电机局部空载磁场分布和铁心磁通密度分布。可见，在此位置时会在定转子齿尖部分产生较为严重的局部饱和现象，此时若仍以简单磁路来等效定转子齿及齿间气隙，将导致电磁性能的计算产生误差，尤其是对气隙磁通密度分布的计算不够准确。

图9 定转子齿槽间磁场分布和磁通密度分布Fig.9 Field distributions and flux density distributions between stator slots and rotor poles

因此，对出现局部饱和现象的区域，本文中以图10 所示的方法来对原等效磁路进行修正。以定子齿为例，图10a 为简化状态下的磁路构成，此时各用一条磁支路来等效定子齿、转子齿和定转子齿之间气隙；而图10b 为修改后的磁路构成，定子齿磁路等效为三条支路，由两条支路并联后再与另一支路串联。其中，两条并联支路分别代表出现局部饱和效应的齿尖区域重叠部分和非重叠部分，此时气隙磁路构成也更为复杂。

图10 不同模型下的定转子齿槽间磁导Fig.10 Air-gap permenaces between stator slots and rotor poles under different magnetic models

通过对磁路的修改来考虑局部饱和现象的影响，可以得到FSPM 电机的初始磁网络模型，如图11 所示。相比较于图8 中的原始磁网络模型，可见进行局部饱和修正后的模型更为复杂，尤其是此时的定转子齿磁路也随转子位置的变化而改变，这进一步增大了模型的复杂程度。

图11 考虑局部饱和效应后的初始磁网络模型，θr=0°Fig.11 The initial magnetic network model considering localized saturation effect,θr=0°

随着转子位置改变，即使同一个定子齿或是转子齿的局部饱和程度也有所不同。故本文以局部饱和深度系数（ksat）来反映局部饱和程度的大小为

式中 hsat——局部饱和深度；

ht——定子齿或转子齿的实际高度，在定子齿和转子齿中，具体意义可参考图10。

3.3 FSPM 电机电磁性能分析结果对比

图12 所示为有限元分析所得FSPM 电机在上述两个典型转子位置下的上半圆周气隙空载永磁磁场分布，而图13 对比了有限元法、原始磁网络模型和初始磁网络模型对以上两个转子位置气隙磁通密度波形的计算结果。由图可见，两种磁网络模型的分析结果与有限元法都较为一致，但由于没有考虑局部饱和效应，原始模型所得气隙磁通密度波形峰值对应位置与有限元法存在较大偏差，而考虑了局部饱和效应的初始模型与有限元分析结果更为一致。本文中令ksat=0.4，为固定值。由图13 可知，修正模型计算所得气隙磁通密度分布的精度显著高于原始模型，尤其是在气隙磁通密度达到各局部峰值的位置。

图12 两个典型转子位置的空载磁场分布，θr=0°及θr=9°Fig.12 Open-circuit field distribution at two typical rotor positions,i.e.θr=0°and θr=9°

图13 两个转子位置的上半圆周空载气隙磁通密度分布波形Fig.13 Air-gap open-circuit flux density distributions waveforms of the half FSPM machine at two rotor positions

另一方面，在FSPM 电机中电枢绕组自感和互感可以由以下公式获得

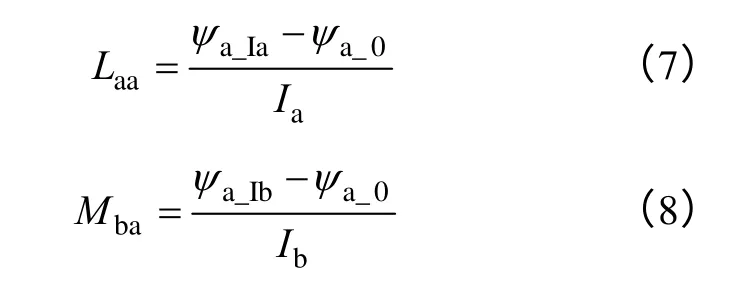
式中 Laa——A 相电枢自感；

Mba——A、B 相间互感；

Ψa_0——A 相永磁磁链；

Ψa_Ia——A 相加载电流时的A 相合成磁链；

Ia——A 相电枢电流；

Ψa_Ib——B 相加载电流时的A 相合成磁链；

Ib——B 相电枢电流。

图14 对比了有限元法、原始模型和初始模型对A 相电枢线圈空载磁通的分析结果，可见三者的计算结果高度一致。然而，当单独给A 相电枢绕组加载8A/mm2的电流密度时（槽满率kpf=0.75），原始模型和初始模型与有限元分析的结果相比有较大偏差，如图15 所示。这是由于加载电枢电流后，导致定子极间漏磁通增大，而本节中上述两种磁网络模型的定子轭部所在区域磁路构成都较为简单，无法准确计及全部的漏磁磁通通路，导致计算结果误差较大。同时，结合式（7）、式（8），这也间接导致上述磁网络模型对FSPM 电机电枢绕组电感（包括不饱和电感）的计算存在较大误差，如图16 所示。

图14 不同模型的电枢线圈空载永磁磁通波形对比Fig.14 Comparisons of the open-circuit coil PM flux waveforms under different predicting models

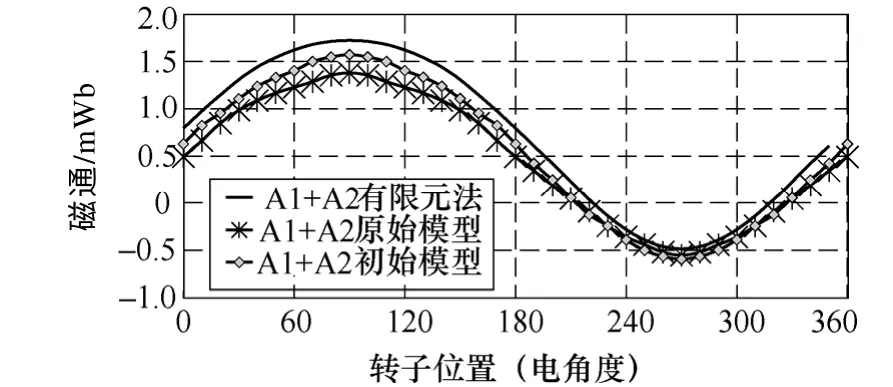
图15 A 相电枢绕组加载8A/mm2 电流密度时的线圈磁通波形的对比，槽满率kpf=0.75Fig.15 Comparison of the coil flux waveforms with phase-A loaded with current density of 8A/mm2,slot pakage factor kpf=0.75

图16 三种模型的电枢绕组自感和互感波形Fig.16 Self- and mutual-inductances under three models

因此，为解决上述问题，本文在初始模型的基础上又提出了多段永磁支路模型和导磁桥模型，需要说明的是，两种新模型均考虑了局部饱和效应，具体见第4 节所述。

4 多段永磁支路模型和导磁桥模型

4.1 改进后的磁网络模型

针对上述磁网络模型计算电感误差较大的情况，并充分考虑加载电枢电流后的定子齿之间的漏磁，本文在初始模型基础上提出了图17 中所示的多段永磁支路模型，以及图18 所示的导磁桥模型。其中，多段永磁支路模型相对于初始模型，一块永磁体等效为三条并行支路，并在两块相邻永磁体的等效磁路间添加了定子极间漏磁通路径；而在图18所示的导磁桥模型中，采用两套串联支路来分别等效定子铁心U 形单元的一个齿和轭部，并在二者之间加入“导磁桥”（bypass-bridge）来为定子轭部与定子齿之间的漏磁磁通提供路径。

图17 多段永磁支路模型，θr=0°Fig.17 Multi-PMs model,θr=0°

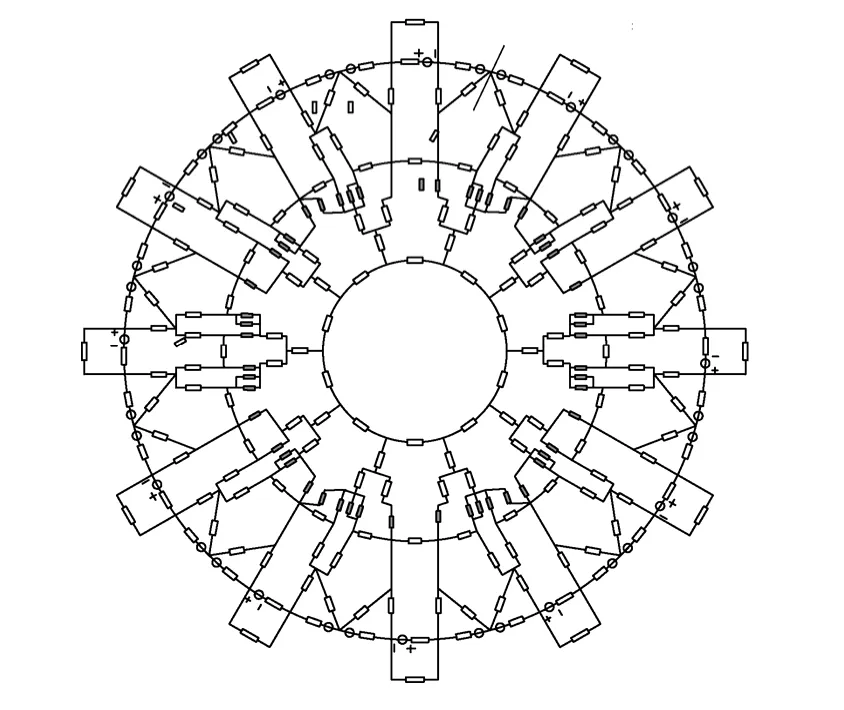
图18 导磁桥模型，θr=0°Fig.18 Bypass-bridge model,θr=0°

4.2 FSPM 电机电磁性能分析结果对比

为验证两种新模型的有效性，本节详细对比二者对各电磁特性的计算结果与有限元分析的差别。

图19 所示为有限元法、多段永磁支路模型和导磁桥模型对FSPM 电机上半圆周气隙空载永磁磁通密度的分析结果的比较。由图可见，两种新磁网络模型分析结果与有限元法较为一致，而导磁桥模型的分析结果更为精确。同时，对于空载电枢磁链，两种新型模型的计算结果也都与有限元高度一致，如图20 所示的。而观察图21，在A 相电枢绕组加载8A/mm2的电流密度时（槽满率kpf=0.75），两种新模型对电枢线圈磁通的计算精度要明显高于初始模型，尤其是导磁桥模型的计算结果，与有限元法保持高度一致。相应的，图22 中对电感计算结果的比较也可说明导磁桥模型具有最高的计算精度。

图19 两个典型转子位置的上半圆周气隙磁通密度分布波形Fig.19 Air-gap flux density distributions waveforms of half FSPM machine at two typical rotor positions

图20 电枢线圈空载磁通波形Fig.20 Open-circuit coil flux waveforms

图21 A 相电枢绕组加载8A/mm2 电流密度时的线圈磁通波形的对比，槽满率kpf=0.75Fig.21 Comparison of the coil flux waveforms with phase-A loaded with current density of 8A/mm2,slot pakage factor kpf=0.75

图22 电枢绕组自感和互感波形Fig.22 Self and mutual inductances of armature windings

5 实验验证

图23 所示为本文中研究的一台三相定子12 槽/转子10 极FSPM 电机实验样机，其参数见表1。通过图24 中对A 相空载感应电动势（电枢单个线圈75 匝，转速1 000r/min）的对比，可见有限元法、磁网络模型和实验测试均能保持高度一致，这也验证了有限元法及所提出的磁网络模型的正确性。需要说明的是，由于端部效应的影响，样机实测感应电动势的幅值略小于有限元计算的结果。

图23 样机照片Fig.23 The prototyped machine

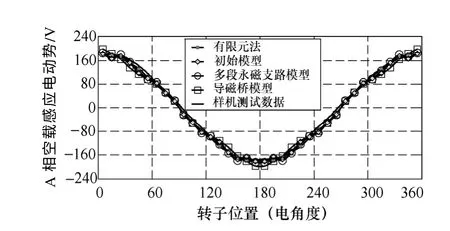
图24 A 相空载感应电动势，转速1 000r/minFig.24 Open-circuit phase-A EMF waveforms at 1 000r/min

6 结论

本文针对一台三相定子12 槽/转子10 极磁通切换型永磁电机（FSPM 电机），提出了一种非线性变结构磁网络模型。该原始模型在考虑了电机铁心内部磁场饱和的前提下，可实现对气隙磁通密度分布、电枢线圈永磁磁通、空载感应电动势等电磁性能的计算。

然后，在原始模型基础之上考虑了局部饱和效应的影响，得到了改进后的初始模型，该模型对气隙磁通密度的计算精度明显高于原始模型，但是两种模型对绕组电感的计算与有限元法仍存在较大偏差。

因此，在初始模型的基础上，又提出了多段永磁支路模型和导磁桥模型。二者均考虑了局部饱和效应的影响，并分别通过对永磁体与定子铁心单元的齿和轭部进行细化处理，得到了更高的计算精度，尤其是对绕组电感的计算与有限元法更为接近。

综上可知，本文所述的FSPM 电机磁网络模型中，导磁桥模型具有最高的计算精度。所建立的磁网络模型计算结果得到了有限元法与实验样机测试的验证。

[1] Soong W L,Ertugrul N.Field weakening performance of interior permanent-magnet motors[J].IEEE Transactions on Industry Applications,2002,38(5):1251-1258.

[2] Cheng Ming,Hua Wei,Zhang Jianzhong,et al.Overview of stator-permanent magnet brushless machines[J].IEEE Transactions on Industrial Electronics,2011,58(11):5087-5101.

[3] Liao Y,Liang F,Lipo T A ． A novel permanent magnet machine with doubly salient structure[J].IEEE Transactions on Industry Applications,1995,31(9):1069-1078.

[4] 张建忠,程明,朱孝勇,等.新型整距绕组双凸极永磁电机工作原理及特性[J].中国电工技术学报,2009,24(2):1-7.

Zhang Jianzhong,Cheng Ming,Zhu Xiaoyong,et al.Principle and analysis of doubly salient permanent magnet machine with novel full-pitch windings[J].Transactions of China Electrotechnical Society,2009.24(2):1-7.

[5] Hoang E,Ahmed A H Ben,Lucidarme J.Switching flux permanent magnet polyphased synchronous machines[C].Proc.7th Europe Conf.Power Electron and Application,1997(3):903-908.

[6] 刘细平,郑爱华,王晨,等.定子分割式轴向磁通切换混合励磁同步电机三维有限元分析与实验研究[J].中国电工技术学报,2012,27(10):106-113.

Liu Xiping,Zheng Aihua,Wang Chen,et al.Principle and analysis of doubly salient permanent magnet machine with novel full-pitch windings[J].Transactions of China Electrotechnical Society,2012,27(10):106-113.

[7] 吴一丰,邓智泉,王宇,等.六相永磁容错磁通切换电机及其单相故障的容错控制[J].中国电工技术学报,2013,28(3):71-79.

Wu Yifeng,Deng Zhiquan,Wang Yu,et al.Six-phase fault-tolerant flux switching permanent magnet motor and control strategy for single-phase fault condition[J].Transactions of China Electrotechnical Society,2013,28(3):71-79.

[8] Boldea I,Zhang J,Nasar S A.Theoretical characterization of flux reversal machine in low-speed servo drives-the pole-PM configuration[J].IEEE Transactions on Industry Applications,2002,38(6):1549-1558.

[9] 花为,程明,Zhu Z Q,等.新型磁通切换型双凸极永磁电机的静态特性研究[J].中国电机工程学报,2006,26(13):129-134.

Hua Wei,Cheng Ming,Zhu Z Q,et al.Study on static characteristics of novel flux-switching doubly-salient PM machine[J].Proceedings of the CSEE,2006,26(13):129-134.

[10] Hua Wei,Cheng Ming,Zhu Z Q,et al.Analysis and optimization of back-EMF waveform of a fluxswitching permanent magnet motor[J].IEEE Transactions on Energy Conversion,2008,23(3):727-733.

[11] 程启明,程尹曼,王映斐,等.交流电机控制策略的发展综述[J].电力系统保护与控制,2011,39(9):145-154.

Cheng Qiming,Cheng Yinman,Wang Yingfei,et al.Overview of control strategies for AC motor[J].Power System Protection and Control,2011,39(9):145-154.

[12] 刘婷婷,谭彧,吴刚,等.基于SVPWM 的高转速永磁同步电机控制系统的研究[J].电力系统保护与控制,2009,37(12):11-19.

Liu Tingting,Tan Yu,Wu Gang,et al.Simulating of high speed PMSM control system based on SVPWM[J].Power System Protection and Control,2009,37(12):11-19.

[13] 王玲芝.改进的永磁同步电机直接转矩控制系统仿真实现[J].电力系统保护与控制,2009,37(19):65-68.

Wang Lingzhi.Simulation of improved direct torque control system for permanent magnet synchronous motor[J].Power System Protection and Control,2009,37(19):65-68.

[14] 程明,周鹗,黄秀留．双凸极变速永磁电机的变结构等效磁路模型[J].中国电机工程学报,2001,21(5):23-28.

Cheng Ming,Zhou E,Huang Xiuliu.Variable structure equivalent magnetic circuit modeling for double salient permanent magnet machine[J].Proceedings of the CSEE,2001,21(5):23-28.

[15] Zhu Z Q,Pang Y,Howe D,et al.Analysis of electromagnetic performance of flux-switching permanent magnet machines by non-linear adaptive lumped parameter magnetic circuit model[J].IEEE Transactions on Magnetics,2005,41(11):4277-4287.