一种大力矩大位移微纳压电致动器的瞬态响应

靳 宏 胡敏强 徐志科 潘非非

（1.东南大学电气工程学院 南京 210096 2.扬州大学水利与能源动力工程学院 扬州 225127）

1 引言

随着科技的发展，作为精密工程和精密仪器的关键技术之一的高精度微位移技术在诸如微电子、微机械、纳米科技、主动光学和光纤对接等许多前沿学科领域都有广泛的需求和应用。进入20 世纪90 年代以来，无论是光电子器件或集成电路的加工还是生物医学工程中的细胞操作，都越来越多的对微纳定位工作平台技术提出了大行程，高精度，小体积和快速响应的要求，其中对定位精度和分辨率的要求提高到了纳米量级[1,2]。

压电陶瓷驱动器因具有位移分辨率高、结构简单、发热小、体积小、刚度高、响应速度快、不受磁场干扰、无磨损、不需润滑等优点被广泛地应用于微纳定位系统中。但压电陶瓷驱动器也存在位移伸长量小，不能承受拉力和扭力，有迟滞、非线性和蠕变等缺点[3]。为了放大位移量，目前多采用铰链形式进行位移量的放大[4-8]，但是却牺牲了输出力矩。为了解决这一问题，本文设计了一种基于压电叠堆、运用三角放大原理的放大机构，实现对微纳定位系统的驱动。

在保证位移精度和输出力矩的同时，提高其位移量。

2 基于正交放大原理的压电叠堆位移放大致动器

位移放大原理采用正交三角放大原理，如图1 所示。设直角三角形的长直角边为b，短直角边为a，长直角边与斜边的初始夹角为θ。当长直角边伸长量为Δb 时，短直角边的缩短量为Δa，则有

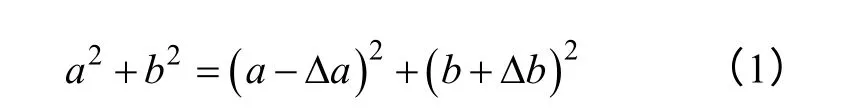
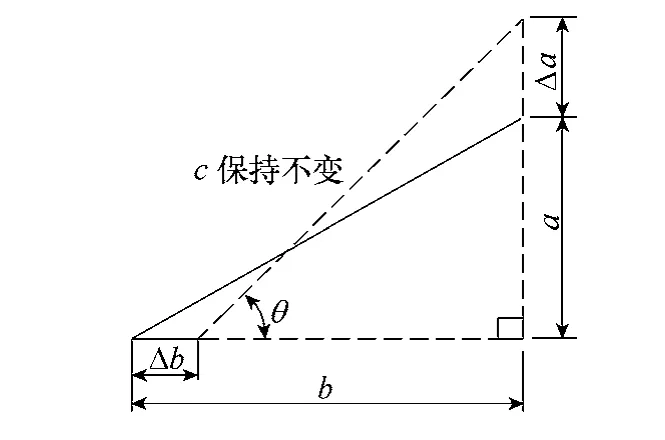
图1 直角三角放大原理示意图Fig.1 The principle diagram of right angled triangle amplification

由式（1）约去二阶小量，可得放大倍数β为

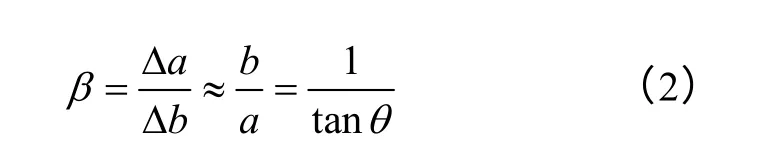
由式（2）可以看出，放大倍数β只与长直角边和斜边的初始夹角θ有关，而与斜边和直角边的长度无关。放大倍数β与初始夹角θ的对应关系如图2 所示。从图中可以看出，随着夹角θ的不断减小，放大倍数β不断增大，且增长的幅度越来越大[9]。

压电叠堆由多片压电陶瓷组成，多层压电陶瓷片胶结为整体，通过内部嵌入电极构成压电叠堆，即叠层型压电致动器；实现在机械上串联、电极上并联，每片陶瓷获得相同的电压，各压电片产生的位移量也就实现了叠加输出，获得较大的输出位移（见图3）。压电叠堆通常被用作驱动元件，利用其逆压电效应将电能转化为机械能，具有输入电压低、变形大、输出力大、响应快、位移可重复性好等优点[10]。

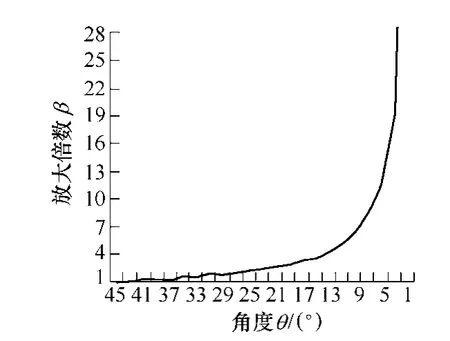
图2 放大倍数β与夹角θ的对应曲线Fig.2 The curve of magnification factor β and intersection angle θ

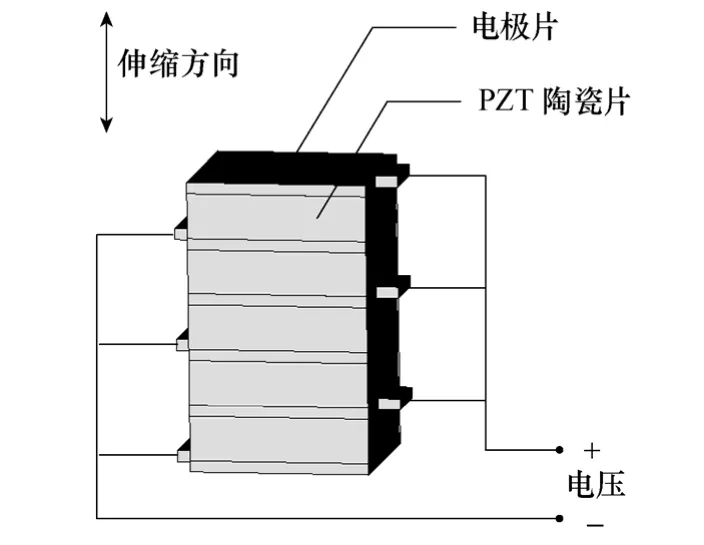
图3 叠层型压电致动器结构示意图Fig.3 The structural diagram of piezoelectric stack actuator

基于正交放大原理的压电叠堆位移放大致动器利用正交三角放大原理，设计成菱形对称结构（见图4）。压电叠堆置于放大机构内部，位于菱形长对角线方向，短对角线方向一端固定一端自由。当压电叠堆两端施加的电压升高时（见图4a），压电叠堆在长对角线方向上产生位移量为δ的伸长形变，经放大机构，在短对角线方向自由端产生位移量为β×δ的收缩形变。反之，当压电叠堆两端施加的电压降低时（见图4b），压电叠堆在长对角线方向上产生位移量为δ的收缩形变，放大机构随之弹性缩回，在短对角线方向自由端产生位移量为β×δ的伸长形变。

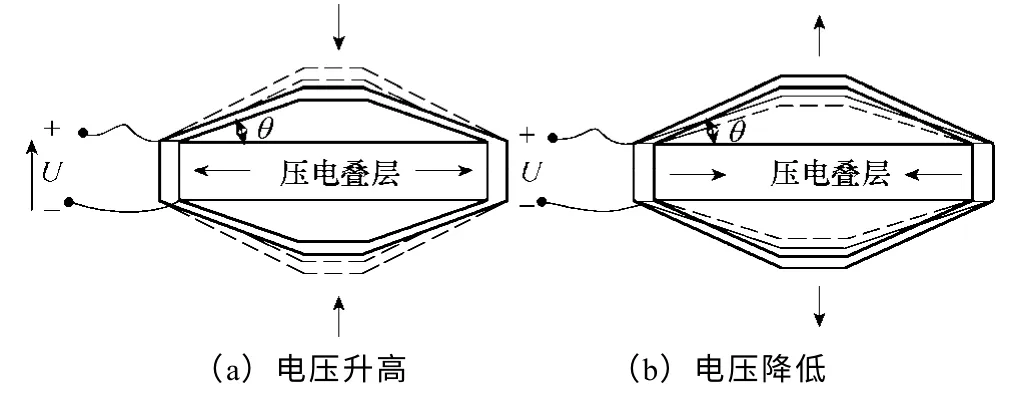
图4 位移放大机构工作原理示意图Fig.4 The operational principle diagram of displacement magnifying mechanism

由于放大机构是利用材料的弹性形变来工作的，且可能工作在较大的负载压力下，所以需要选择既有良好的弹性恢复能力，又有一定刚度的材料。本机构选择45#钢来加工放大机构，压电叠堆作为驱动部件，得到压电叠堆位移放大致动器实物图如图5 所示。

图5 压电叠堆位移放大致动器样机图Fig.5 The prototype diagram of piezoelectric stack displacement magnifying mechanism

运用三角放大原理放大位移量后的压电叠堆不仅能输出较大的位移量，还能提供较大的输出力矩，具有很好的响应速度，因此具有较广泛的应用前景。实际应用中，不仅需要对这种致动器的静态特性、固有特性进行分析研究，还需要关注其在通入激励电压和撤除激励电压时，致动器的瞬态响应特性。

3 压电叠堆位移放大致动器瞬态响应特性的理论分析

3.1 通入激励电压时

由于有限元法采用了离散处理，所以它的计算更为简单，处理的问题更为复杂，具有非常广泛的实用价值。其动态分析的有限元法不仅可以对结构的固有特性进行分析，还可以计算结构对给定动载荷的各种响应特性。

本文运用ANSYS 有限元分析软件对压电叠堆位移放大致动器的瞬态响应特性进行动态分析。分析在t=0 时，向压电叠堆通入阶跃激励电压，致动器随时间变化的位移变化情况。

瞬态动力学分析（有时称时间-历程分析）是用于确定承受任意随时间变化载荷的结构的动力学响应的一种方法。可以使用这种方法来确定结构在静载荷、瞬态载荷和简谐载荷的任意组合作用下的随时间变化的位移、应力和力。载荷和时间的相关性使得惯性力与阻尼作用非常重要，不能忽略。

瞬态动力分析求解的基本方程如下：

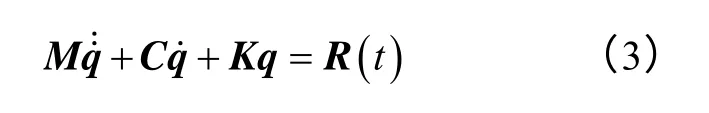
式中，M、C、K 分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；为节点加速度矩阵；为节点速度矩阵；q 为节点位移矩阵；R(t)为节点载荷矢量。

最后，通过直接积分法对微分方程（3）进行求解[11]。本文运用ANSYS 有限元分析软件对致动器模型进行有限元计算分析，压电叠堆是极化方向为Z 方向的压电材料，放大机构是金属钢，对压电叠堆加载不同的电压即可得到致动器位移量随时间变化的瞬态响应结果。运用瞬态响应分析时，设置步长为0.075ms，计算时长为0～100ms。最后运用后处理方式获得输出结果如图6 和图7 所示。

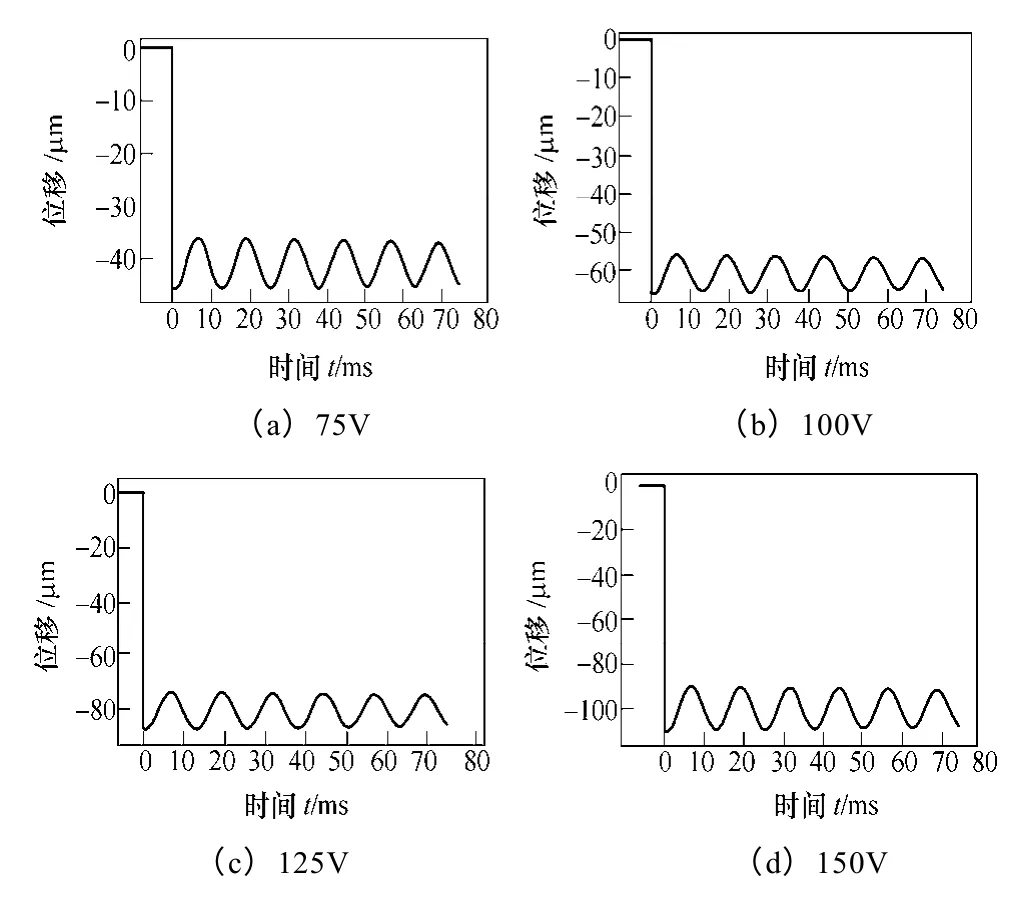
图6 通入不同激励电压时，致动器的瞬态响应理论分析曲线Fig.6 Transient response diagrams adding different voltages in theory analysis

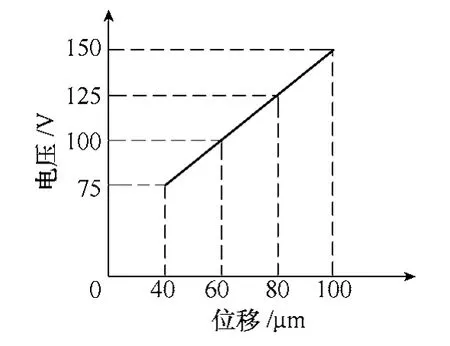
图7 激励电压-位移图Fig.7 Voltage-displacement diagram

3.2 撤除激励电压时

由于压电叠堆实质上就是一个容性负载，在不增加放电回路的情况下，断电2 分钟后，压电叠堆的残余电压仍然有3～4V，放电时间较长；所以通过增加电阻对其进行撤除激励电压的瞬态分析。因此对这种致动器进行撤除电压的瞬态理论分析，实际上是分析一个电容的放电过程，其特性方程为

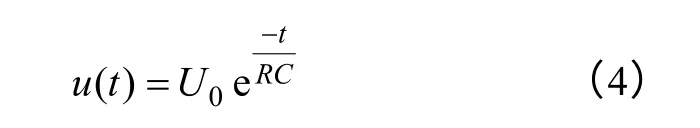
结合实际的实验测试情况，被测压电叠堆的电容值为6.14μF，采用一个10kΩ/4W 的电阻进行放电。本文运用Matlab 软件对这一过程进行仿真分析后，得到撤除激励电压时的瞬态特性仿真图如图8 所示。

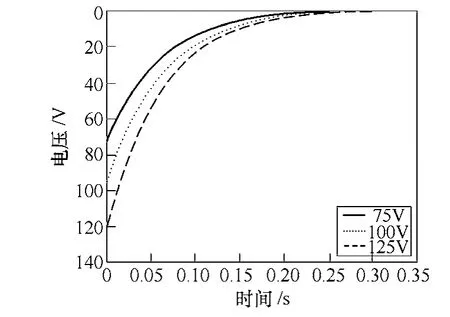
图8 撤除激励电压时的瞬态特性仿真图Fig.8 The simulation diagram of transient characteristic when removing the voltage

3.3 计算结果分析

根据以上的理论分析可知：在通入激励电压时，这一致动器的响应速度非常快，且波动较小，具有很好的瞬态响应速度；压电致动器在不同电压下产生不同的收缩位移量，电压越大，位移量越大，位移量随电压变化的线性度也非常好。在撤除激励电压时，虽然加载在压电叠堆上的初始电压不同，得到了不同的变化曲线，但是其放电时间却是基本一致的；经过0.3s，压电叠堆放电基本完成，致动器回复到原始状态。

4 压电叠堆位移放大致动器瞬态响应特性的实验分析

4.1 实验测试装置及方法

为进一步从实验角度对这一致动器的瞬态响应特性进行掌握，运用动态投影栅线法对致动器进行了实验研究。

动态投影栅线法是将一组正弦栅线投影到被测物体表面，用高速摄像机记录下被测表面随时间变化时不同的条纹图，经相位差去包裹，以及加窗傅里叶变换后，获得其在不同时间的位移情况[12-14]。动态特性测试的装置图如图9 所示。由LG-Ⅲ提供冷光源，经投影仪后，将频率为5lines/mm 的正弦栅线投射到压电致动器的被测面上；高速摄像机以4 000 帧/s 的采样频率将连续变化的栅线图记录到计算机中，经计算分析，得到压电致动器的瞬态响应特性。

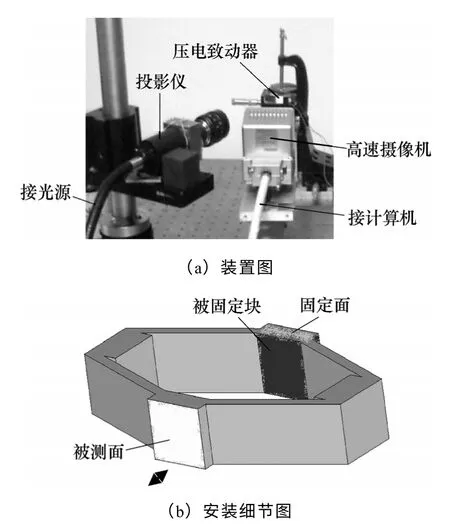
图9 动态特性测试装置图Fig.9 Equipment diagram of dynamic characteristic test

对压电致动器进行瞬态特性测试的接线图如图10 所示。开关K 放在“1”处时，电源立即向压电致动器中的压电叠堆供电，压电叠堆伸长，压电致动器收缩，被测面离面位移减小（为负），即可测得致动器通入激励电压时位移随时间变化的瞬态特性。开关K 放在“3”处时，压电叠堆所存储的电场能立即通过电阻R1放电，压电叠堆收缩，压电致动器伸长，被测面离面位移增加（为正），即可测得致动器撤除激励电压时位移随时间变化的瞬态特性；若需要提高放电速度，将开关K 放在“2”处时，即可增加一个并联电阻R2，减小放电电阻的同时，缩短放电时间，提高压电致动器的响应速度。

图10 压电致动器接线图Fig.10 The connection diagram of piezoelectric actuator

4.2 测试结果

运用动态投影栅线法对通入和撤除激励电压的瞬态特性进行测试，得到致动器通入75V、100V、125V、150V 电压后的位移-时间响应特性曲线如图11 所示；在三种电压75V、100V、125V 下，撤除激励电压的放电瞬态特性如图12 所示。

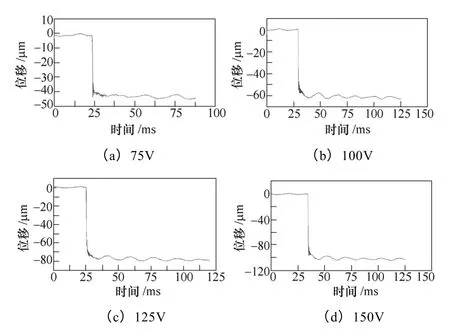
图11 通入激励电压时的瞬态特性实测图Fig.11 Transient characteristic diagrams adding different voltages in actual measurement

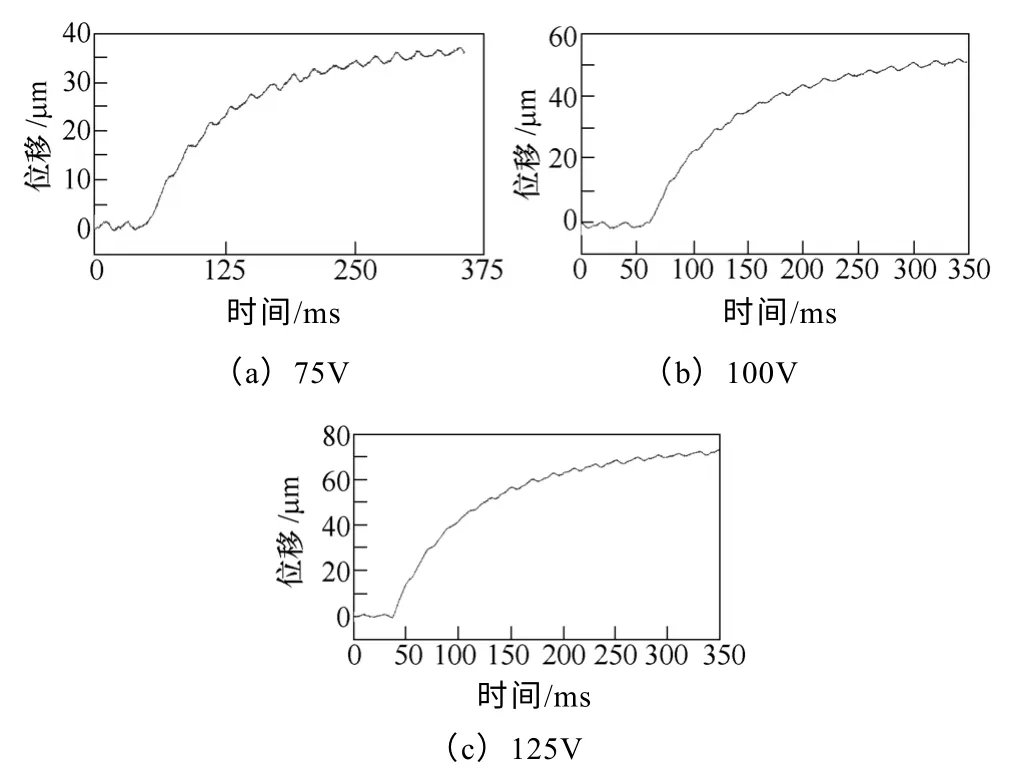
图12 撤除激励电压时瞬态特性实测图Fig.12 Discharge’s transient characteristic diagram under different voltages in actual measurement

由图11 可知，通入激励电压时，在很短的时间内（小于0.5ms）压电致动器产生了相应的突变收缩位移；之后受到放大装置自身抖动的影响，压电致动器在一个很小的范围内有一定的波动，并随时间推移而逐渐减小，由于这个波动远小于通电时的突变位移，所以在实际应用中可忽略其影响。同时，还可以看到这种压电致动器的位移量与理论分析结果相同，随电压变化的线性度很好。因此，这一致动器在通电时实测结果与理论分析结果从位移量和线性度上都非常接近，具有较好的通电瞬态响应特性。

从图12 可知，撤除激励电压时，这种压电致动器在经过约0.3s（与理论分析相符）后，其放电过程基本完成，且动态位移过程平稳，与Matlab 分析情况相同；只是这种压电致动器位移的回零较差，没能很好的实现收缩位移还原，这与压电叠堆的回零差有关。在实际应用中，若需要进一步提高它的放电速度，可以通过并接电阻的方式，减小放电的电阻值，从而实现加快放电速度。由此可知，这种压电致动器的放电瞬态响应特性也很好。

5 总结

本文基于正交放大原理，运用压电叠堆设计并制造了具有大位移、大力矩、不受电磁干扰的致动器。通过有限元分析软件、Matlab 软件、以及动态投影栅线法，从理论和实验两个方面对这种致动器在通入和撤除激励电压时的瞬态响应进行了计算分析。

根据理论和实测结果，证明了这种基于三角放大原理的压电叠堆位移放大致动器具有很好的瞬态响应特性，其理论和实测结果相近。在通入激励电压时，具有很快的响应速度和特性，而且电压和位移的线性度也非常好。在撤除激励电压时，运用电阻放电，得到的响应特性过程平稳，时间随电阻值不同而实现不同的放电和位移变化速度。因此，这种致动器从瞬态分析上可以看出，它可以被广泛地运用于微纳控制系统中，为微纳系统提供可靠、快速的大位移大力矩驱动部件。

[1] Li Cheng,Zhang Chengjin,Guilin Zhang.High-speed and Large-range scanning control of a piezoelectric stack actuated platform[C].Proceedings of the 8th World Congress on Intelligent Control and Automation,Jinan,China,2010:5523-5527.

[2] Li Yangmin,Xu Qingsong.Development and assessment of a novel decoupled xy parallel micropositioning platform[J].IEEE/ASME Transactions on Mechatronics,2010,15(1):125-135.

[3] 孙宝玉.柔性压电式微位移机构动态特性的实验研究[J].微细加工技术,2008(2):33-36.

Sun Baoyu.Experimental research on dynamic charateristic of flexible micrro-displacement mechanism based on piezoelectric actuator[J].Micro Fabrication Technology,2008(2):33-36.

[4] 杜习波,陈西平,张斌,等.基于三角原理的压电驱动微位移定位机构的设计与分析[J].航空精密制造技术,2009,45(6):10-12.

Du Xibo,Chen Xiping,Zhang Bin,et al.Design and analysis of micro-displacement mechanism for motion position with piezo-actuator based on triangle prinple[J].Aviation Precision Manufacturing Technology,2009(6):10-12.

[5] 刘登云,杨志刚,程光明,等.压电叠堆泵微位移放大机构的试验研究[J].机械与电子,2007(3):75-77.

Liu Dengyun,Yang Zhigang,Cheng Guangming,et al.Study on a micro- displacement magnifying mechanism used on piezo-stack pump[J].Machinery & Electronics,2007,3:75-77.

[6] Li Wanquan,Gao Changyin.Design and modeling of micro-displacement amplifying mechanism using revolute joints and flexible hinges[C].International Conference on Intelligent Computation Technology and Automation,2010:1147-1150.

[7] Sebastian Polit,Dong Jingyan.Development of a highbandwidth xy nanopositioning stage for high-rate micro-nanomanufacturing[J].IEEE/ASME Transactions on Mechatronics,2011,16(4):724-733.

[8] Xu Qingsong,Li Yangmin,Xi Ning.Design,fabrication,and visual servo control of an xy parallel micromanipulator with piezo-actuation[J].IEEE Transactions on Automation Science and Engineering,2009,6(4):710-719 .

[9] 徐志科,鄢珂,金龙.一种正交型压电位移放大机构的研究[J].压电与声光,2009,31(2):207-212.

Xu Zhike,Yan Ke,Jin Long.Research of orthoconal micro-displacement amplifier with piezoelectric actuator[J].Piezo electectrics & Acoustooptics,2009,31(2):207-212.

[10] Tao Shuai.Theoretical and test study on piezoelectric actuator based on micro-vibration isolation plate[J].Master paper,OEC,2008.

[11] 杜平安,甘娥忠,于压婷.有限元-原理、建模及应用[M].北京:国防工业出版社,2011.

[12] Kemao Q.Two-dimensional windowed Fourier transform for fringe pattern analysis:principles,applications and implementations[J].Optics and Lasers in Engineering,2007(45):304-317.

[13] 史红健,朱飞鹏,何小元.动态投影栅线的加窗傅里叶分析方法[J].东南大学学报（自然科学版）,2010,40(2):409-413.

Shi Hongjian,Zhu Feipeng,He Xiaoyuan.Windowed Fourier analysis for dynamic fringe projection[J].Journal of Southeast University (Natural Science Edition),2010,40(2):409-413.

[14] Duan Cunli,Zhang Sujuan,He Xiaofeng.Research of three-dimensional surface detection method based on grating projection[C].International Conference on Electronics and Optoelectronics (ICEOE 2011),2011,2:335-338.