磁极分段型表贴式永磁电机建模与分析

杨思雨 夏长亮, 王慧敏 史婷娜

（1.天津大学电气与自动化工程学院 天津 300072 2.天津市电工电能新技术重点实验室（天津工业大学）天津 300387）

0 引言

永磁电机因具有高效率、高转矩密度、高转矩电流比以及低维修成本等特点，近年来在电动汽车、数字控制装置以及机器人技术等高性能驱动领域得到了广泛应用。然而，定子齿部与永磁体相互作用所产生的齿槽转矩以及定子电流与转子磁场相互作用所产生的电磁转矩波动[1-3]，常引起电机振动及噪声，降低驱动系统控制精度。因此，削弱转矩波动是电机设计过程中需要重点考虑的问题。

从电机设计角度考虑，削弱转矩波动的主要方法包括极槽配合、极弧系数优化、斜极或斜槽、增加辅助槽、磁极形状优化、槽口偏移等[4-8]。文献[9]提出使用磁极分段的方法削弱永磁电机齿槽转矩，并利用有限元算法得到了不同分段参数下的齿槽转矩变化规律。磁极分段不会过于增加电机结构的复杂性。对于直径较大的永磁电机，单块磁极的制造有一定困难，磁极分段同时能够降低电机制造成本。在文献[9]的基础上，文献[10]结合有限元算法与近似气隙磁路模型，对磁极分段型永磁同步电机进行了分析与优化。文献[11]采用简化气隙磁场模型结合特定谐波消除法确定磁极分段参数。

磁极分段会使得电机磁场发生畸变，增加磁场分析的复杂性。由于有限元方法的建模过程较为复杂，因此建立磁极分段型永磁电机的解析模型有助于分析电机性能随磁极分段参数的变化规律，对于提高电机性能具有重要意义。精确子域模型[12-15]能够考虑定子槽间相互影响，对永磁电机定子开槽后的磁场进行准确计算。

本文在推导分段磁极磁化强度的基础上对精确子域模型进行扩展，针对径向与平行充磁条件下任意磁极分段数目的表贴式永磁电机（Surface Mounted Permanent Magnet Machines，SMPM），将永磁体、气隙、定子槽口以及定子槽身作为研究区域，对矢量磁位进行求解，并计算各区域内磁场分布，进而对电机齿槽转矩与相反电动势进行计算。该模型适用于永磁体平行与径向充磁方式下的磁极分段型表贴式永磁电机。文中以4 极24 槽与8 极12 槽永磁电机为例，研究了电机性能随磁极分段数目与磁极分段位置等参数的变化规律，为磁极分段型永磁电机的设计与优化提供参考。

1 磁场解析模型

本文基于考虑齿尖影响的精确子域模型，推导磁极分段条件下永磁体磁化强度表达式，并对矢量磁位拉普拉斯/泊松方程进行求解，进而对齿槽转矩以及相反电动势进行计算。

1.1 解析模型的建立

为了便于对永磁电机的电磁特性进行分析，首先作如下假设:①永磁体相对磁导率为1；②忽略电机端部效应；③铁心磁导率为无穷大，忽略电机饱和效应；④忽略定、转子涡流效应；⑤每极磁块分段宽度相等。

本文所建立磁极分段型表贴式永磁同步电机解析模型如图1 所示。图中，Rr为转子铁心外半径；Rm为永磁体外半径；Rs为定子铁心内半径；Rt为定子槽顶部半径；Rsb为定子槽底部半径；boa为槽口处所对应圆心角；bsa为槽身处所对应圆心角；θi为第i 个槽中心线机械角度，r、θ 分别为圆心距与圆周角。在二维极坐标系下将解析模型分为4 个区域:区域1 为永磁体；区域2 为气隙；区域3i 为第i 个槽身；区域4i 为第i 个槽口。

在区域1 中，磁场密度B 可表示为

图1 磁极分段型表贴式永磁同步电机解析模型Fig.1 Analytical model of SMPM with segmented pole

在区域2、3i、4i 中，磁场密度B 可表示为

式中，μ0为真空磁导率；μr为永磁体相对磁导率；H 为磁场强度；M 为永磁体磁化强度。

1.2 永磁体磁化强度计算

在永磁体域中，矢量磁位A 与永磁体磁化强度M 之间存在关系

在二维磁场中，矢量磁位仅包括垂直分量Az1，且满足泊松方程

磁极分段型表贴式永磁电机每对极下永磁体分布如图2 所示。

图2 每极永磁体分布示意图Fig.2 Schematic of PM distribution

当αpm=1 时，相当于磁块不分段的情况。令θmi为第i 块分段磁块对称轴所对应的机械角度，可表示为

分别对径向充磁和平行充磁情况进行分析，可知在每对极下磁化强度分布如下:

（1）在N 极第i 段磁块处，即θmi-d2/2＜θ＜θmi+d2/2 时，有

（2）在S 极第i 段磁块处，即2π/p-(θmi+d2/2)＜θ＜2π/p-(θmi-d2/2)时，有

（3）在磁极分块间隙处，即θ 为其他值时，有

式中，Mr、Mθ为分别为磁化强度径向与切向分量。

在整个圆周范围内对永磁体磁化强度分布进行傅里叶分解可得:对于径向充磁，有

则式（4）中Mr与Mθ可表示为

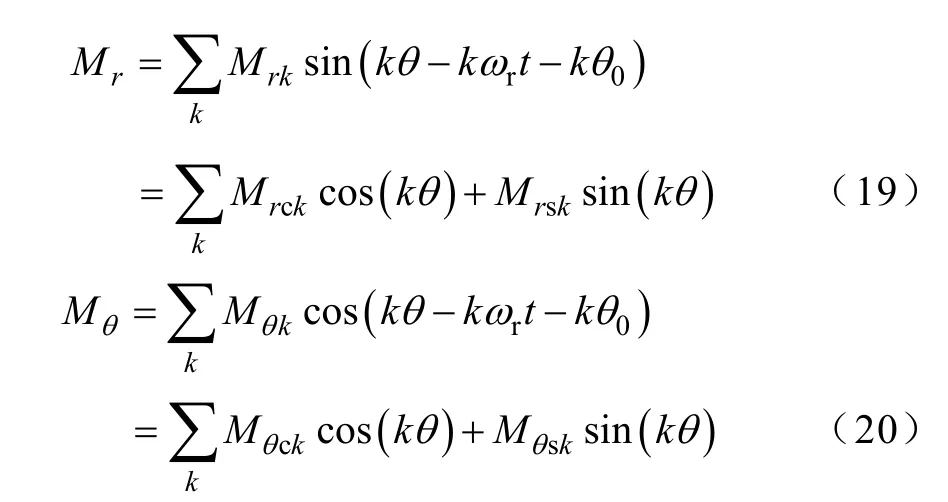
式中，Mrsk、Mrck、Mθsk、Mθck分别为磁化强度在径向与切向上的正弦和余弦分量幅值；ωr为转子角速度；t 为时间；θ0为转子初始位置；k 为各谐波次数。

1.3 矢量磁位与磁场分布求解

在区域1 中，矢量磁位满足式（3）给出的泊松方程；在区域2、3、4 中，矢量磁位均满足拉普拉斯方程

故在图1 所示各区域中，矢量磁位通解可表示如下。

（1）在永磁体域1 内，有

（2）在气隙域2 内，有

（3）在第i 个槽身区域3i 内，有

（4）在第i 个槽口区域4i 内，有

式中，k、n、m 为对应区域中各谐波次数；A1k～D1k、A2k～D2k、C3in、D3in、C4im、D4im为待定系数，可以通过式（27）中各区域磁场边界条件解得。

各区域中磁通密度分布径向分量 Br与切向分量Bθ可由式（28）计算得到。

1.4 齿槽转矩与反电动势计算

根据气隙区域中磁通密度分布计算结果，可得电机齿槽转矩Tcog与各相绕组反电动势Ex分别为

式中，la为电机轴向长度；x 表示定子绕组A、B、C 相；ψx为各向磁链；Nc为每槽导体数；a 为并联支路数。

2 有限元验证

为验证本文所建立模型的准确性，以磁极分段参数α′p=0.9、αpm=0.9 的永磁电机（电机参数见表1）为例，分别对4 极24 槽、nseg=4 以及8 极12 槽、nseg=3 的情况，利用本文所建立解析计算模型与商业电磁场有限元软件对气隙磁场、齿槽转矩与相反电动势进行计算，对解析模型计算结果进行验证，其结果如图3～图5 所示。

由图3～图5 的对比结果可以看出，对于两种充磁方式的磁极分段型表贴式永磁电机，利用所建立的解析模型计算得到的气隙磁通密度、齿槽转矩以及相反电动势波形均与有限元分析结果相一致，验证了本文所建立的解析模型的有效性。由图3 的气隙磁通密度计算结果可以看出，磁极分段对于气隙磁通密度的径向和切向分量均具有较大的影响，在磁极分段处气隙磁通密度各分量均存在尖峰，影响气隙磁通密度分布，使波形产生畸变。由图4 与图5 的计算结果可以看出，由于充磁方式、极槽配合以及分段数目的影响，电机齿槽转矩与相反电动势的波形也会随之发生变化。

表1 磁极分段型表贴式永磁电机基本参数Tab.1 Basic parameters of SMPM with segmented pole

图3 电机气隙磁通密度对比结果Fig.3 FE and analytical predicted air-gap flux density

图4 齿槽转矩对比结果Fig.4 FE and analytical predicted cogging torque

图5 A 相反电动势对比结果Fig.5 FE and analytical predicted back-EMF of phaseA

3 磁极分段型表贴式永磁电机性能分析

3.1 分段数目影响分析

为了分析磁极分段数目对电机性能的影响，利用本文所建立的磁场解析模型对每极分段数为1～6，磁极分段参数α′p=0.9、αpm=0.9 的永磁电机的齿槽转矩以及反电动势进行计算，分别得到图6 所示的齿槽转矩（Tcog）波形以及表2 的反电动势基波幅值（Ef）和总谐波畸变率（E_THD）的计算结果。

从图6 所示的齿槽转矩计算结果可以看出，磁极分段不会改变电机齿槽转矩周期。对于4 极24槽永磁电机，当nseg=2,3,5,6 时，齿槽转矩幅值相对于不分段情况均有不同程度的增加，而当nseg=4时，可以实现有效削弱齿槽转矩的效果。对于8 极12 槽永磁电机，当nseg=4,5,6 时，齿槽转矩幅值相对于不分段情况并未有明显变化，当nseg=2 时，可以有效削弱齿槽转矩。此外，当nseg=3 时，齿槽转矩幅值会有显著增加，使电机性能恶化。因此，对磁极分段型永磁电机进行设计时，为了有效地削弱齿槽转矩，需要针对不同极槽数合理选择磁极分段数目，以实现优化电机性能的目的。

图6 不同分段数目下齿槽转矩波形Fig.6 Cogging torque waveforms with different nseg

表2 不同分段数目下反电动势基波幅值及总谐波畸变率Tab.2 Efand E_THD with different nseg

从表2 给出的不同分段数目下反电动势基波幅值以及总谐波畸变率计算结果可以看出，对于两种极槽配合的永磁电机，磁极分段均会在不同程度上削弱反电动势基波幅值，在电机设计中可以采用增加绕组匝数等方式加以弥补。此外，由反电动势谐波含量计算结果可以看出:对于4 极24 槽电机，当nseg=2 时，反电动势谐波含量明显增加；而对于8极12 槽电机，当nseg=3 时，反电动势谐波含量同样明显高于采用其他分段数的电机。因此，在进行磁极分段式永磁同步电机设计时，需要充分考虑磁极分段数目对于反电动势的影响，使之对电机性能的不良影响降到最低。

3.2 分段位置影响分析

为了分析不同分段位置对电机性能的影响，利用所建立解析模型，分别以4 极24 槽、nseg=4 以及8 极12 槽、nseg=3 的磁极分段型永磁电机为例进行分析，分别计算齿槽转矩幅值（Tcog_max）及反电动势谐波畸变率随α′p以及αpm的变化规律，如图7 与图8 所示。

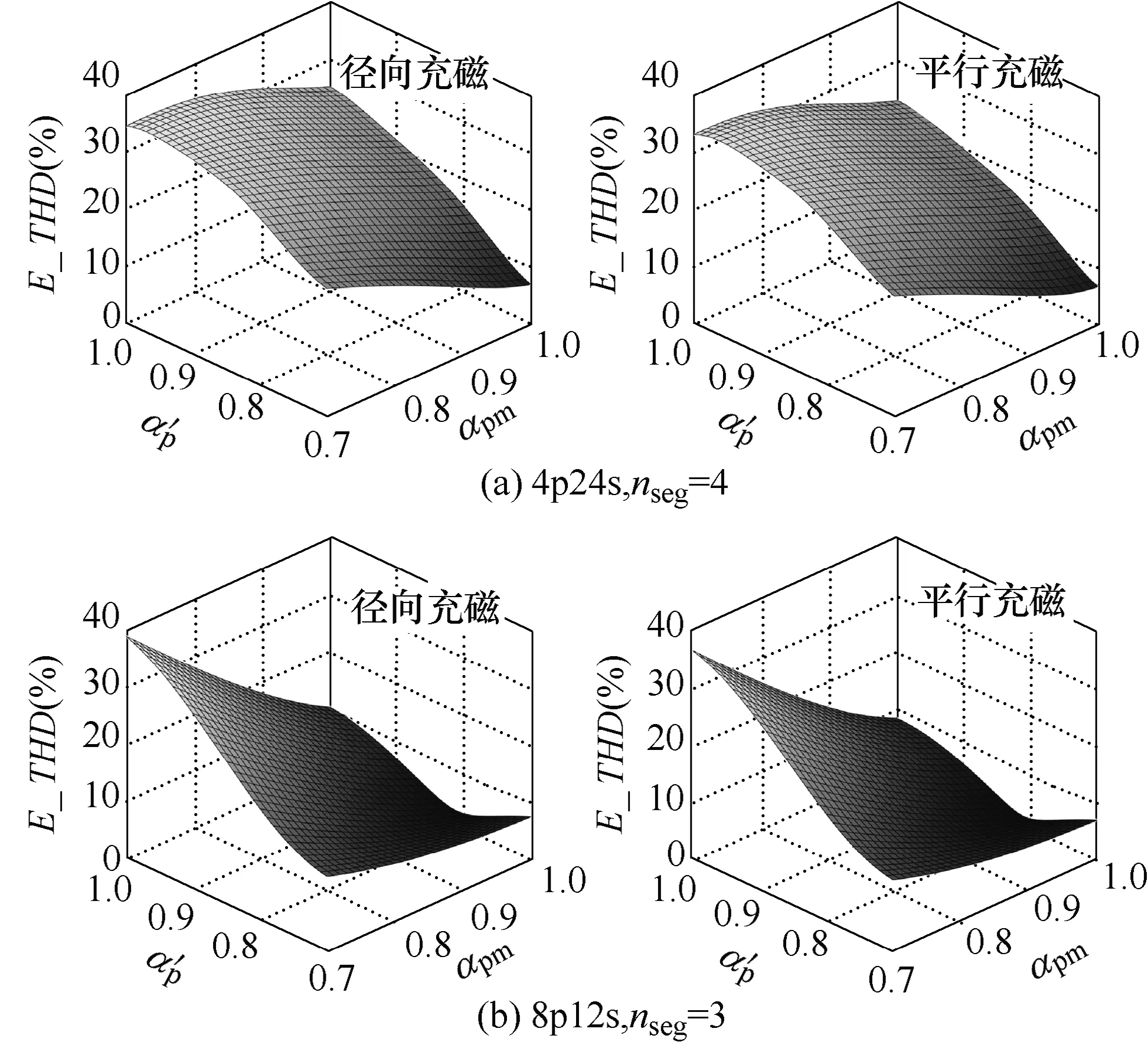
图8 相反电动势总谐波畸变率随分段位置变化规律Fig.8 Variation of back-EMF THD with α′pand αpm

图7 反映了两种极槽配合下电机齿槽转矩峰值随分段位置变化规律。从图7a 可以看出，对于4极24 槽电机，nseg=4 时，齿槽转矩峰值随α′p以及αpm的变化较为复杂，在α′p=0.9、αpm=0.8 以及α′p=0.75、αpm=0.75 附近存在极小值点。在α′p=0.9、αpm=0.8 的极小值附近时，齿槽转矩幅值变化较为平缓；在α′p=0.75、αpm=0.75 的极小值附近时，齿槽转矩幅值变化趋势较大，说明此时若加工误差不能满足要求时，会引起电机性能发生较大的改变。从图7b 可以看出，对于8 极12 槽电机，nseg=3 时，当α′p=0.9、αpm=0.75 时，齿槽转矩峰值达到极大值1.8N·m；当α′p=0.75，αpm=0.95 时，齿槽转矩峰值达到极小值0.05N·m。由以上分析可知，对于不同极槽配合以及每极分段数的磁极分段型表贴式永磁电机，当α′p以及αpm的取值不同时，会使得齿槽转矩峰值出现较大变化，因此在设计时充分考虑不同参数对齿槽转矩的影响。

图8 给出了反电动势谐波含量随分段位置的变化规律。从图8a 可以看出，对于4 极24 槽永磁电机，反电动势总谐波畸变率极小值点出现在α′p=0.7、αpm=1 处，此时相当于磁极未分段情况，说明在这种极槽配合以及每极分段数条件下，磁极分段并不能改善反电动势总谐波畸变率。从图8b 可以看出，对于8 极12 槽电机，反电动势总谐波畸变率极小值点出现在α′p=0.75、αpm=0.95 处，此时反电动势总谐波畸变率约为5%。由以上分析可知，参数α′p与αpm对于电机反电动势总谐波畸变率具有较大的影响，这一点需要在设计时充分考虑，避免造成电机性能的削弱。

由以上分析可知，齿槽转矩峰值与反电动势总谐波畸变率随参数α′p与αpm的变化规律并不一致，需要在多个性能指标之间选择平衡点。此外，在对磁极进行分段时，如果相关参数选择不合理，可能会在气隙磁场中引入高次谐波，使得电机齿槽转矩增加，反电动势谐波含量增大，电机性能无法得到改善，甚至恶化。因此，在对磁极分段型表贴式永磁电机进行设计时，需要合理选择分段参数，使之达到提高电机性能的效果。

4 结论

本文建立了磁极分段型表贴式永磁电机磁场解析模型，该模型适用于磁极均匀分段条件下具有任意分段数目的表贴式永磁电机。以4 极24 槽与8极12 槽电机为例，对磁极分段型表贴式永磁电机进行分析。研究表明，对于不同极槽数的电机，均存在特定的能够显著削弱齿槽转矩的磁极分段数。另一方面，齿槽转矩峰值与反电动势谐波含量随参数α′p与αpm的变化规律并不一致，在设计时需要充分考虑加工精度以及制造成本等因素合理选择磁极分段参数。

[1]Islam M S,Mir S,Sebastian T.Issues in reducing the cogging torque of mass produced permanent magnet brushless DC motor[J].IEEE Transactions on Industry Applications,2004,40(3):813-820.

[2]韩雪岩,陈全文,陈萍.轨道交通用永磁同步牵引电机电抗参数的有限元分析[J].电气技术,2013(3):1-4.Han Xueyan,Chen Quanwen,Chen Ping.The finite element analysis of permanent magnet synchronous traction motor reactance parameters[J].Electrical Engineering,2013(3):1-4.

[3]安忠良,李国丽,周挺.内置式永磁发电机隔磁磁桥形状对齿槽转矩的影响[J].电气技术,2014(4):1-4,19.An Zhongliang,Li Guoli,Zhou Ting.Cogging torque improvement for interior permanent magnet generator by changing flux-barrier shape[J].Electrical Engineering,2014(4):1-4,19.

[4]Bianchi N,Bolognani S.Design techniques for reducing the cogging torque in surface-mounted PM motors[J].IEEE Transactions on Industry Applications,2002,38(5):1259-1265.

[5]Wang K,Zhu Z Q,Ombach G.Torque enhancement of surface-mounted permanent magnet machine using third-order harmonic[J].IEEE Transactions on Magnetics,2014,50(3):104-113.

[6]Shah S Q A,Lipo T A,Kwon B I.Modeling of novel permanent magnet pole shape SPM motor for reducing torque pulsation[J].IEEE Transactions on Magnetics,2012,48(11):4626-4629.

[7]黄守道,刘婷,欧阳红林,等.基于槽口偏移的永磁电机齿槽转矩削弱方法[J].电工技术学报,2013,28(3):99-106.Huang Shoudao,Liu Ting,Ouyang Honglin,et al.A Method for reducing cogging torque by slot-opening shift in permanent magnet motors[J].Transactions of China Electrotechnical Society,2013,28(3):99-106.

[8]夏加宽,于冰,黄伟.减小齿槽转矩的永磁电机结构优化设计[J].电气技术,2009(12):23-25.Xia Jiakuan,Yu Bing,Huang Wei.Optimization of the structure to reduce the cogging torque in pm motors[J].Electrical Engineering,2009(12):23-25.

[9]Lateb R,Takorabet N,Meibody-Tabar F.Effect of magnet segmentation on the cogging torque in surface mounted permanent magnet motors[J].IEEE Transactions on Magnetics,2006,42(3):442-445.

[10]Ashabani M,Mohamed Y.Multiobjective shape optimization of segmented pole permanent magnet synchronous machines with improved torque characteristics[J].IEEE Transactions on Magnetics,2011,47(4):795-804.

[11]Chaithongsuk S,Takorabet N,Meibody-Tabar F.On the use of pulse width modulation method for the elimination of flux density harmonics in the air-gap of surface PM motors[J].IEEE Transactions on Magnetics,2009,45(3):1736-1739.

[12]Zhu Z Q,Wu L J,Xia Z P.An accurate subdomain model for magnetic field computation in slotted surface mounted permanent magnet machines[J].IEEE Transactions on Magnetics,2010,46(4):1100-1115.

[13]郭思源,周理兵,曲荣海,等.基于精确子域模型的游标永磁电机解析磁场计算[J].中国电机工程学报,2013,33(30):71-80.Guo Siyuan,Zhou Libing,QuRonghai,Ling Zaixun.Analytical magnetic field calculation of vernier permanent magnet machines based on accurate subdomain model[J].Proceedings of the CSEE,2013,33(30):71-80.

[14]李节宝,井立兵,周晓燕,等.表贴式永磁无刷电机直接解析计算方法[J].电工技术学报,2012,27(11):83-88.Li Jiebao,Jing Libing,Zhou Xiaoyan,et al.Exact analytical method for surface-mounted permanent magnet brushless motors[J].Transactions of China Electrotechnical Society,2012,27(11):83-88.

[15]郭思源,周理兵,齐歌.双三相永磁同步电机电磁性能解析计算[J].电工技术学报,2014,29(5):17-28.Guo Siyuan,Zhou Libing,Qi Ge.Analytical calculation of electromagnetic performance in dual three-phase permanent magnet brushless AC machines[J].Transactions of China Electrotechnical Society,2014,29(5):17-28.