基于PSCAD 的大规模钳位双子模块-模块化多电平换流器高效仿真建模方法

刘崇茹 洪国巍

（新能源电力系统国家重点实验室（华北电力大学）北京 102206）

0 引言

模块化多电平换流器（Modular Multi-level Converter,MMC）是采用模块化设计的新型电压源换流器。MMC 能够独立控制有功、无功功率，输出电压、电流波形质量高，模块化扩展性好，因而被广泛关注。最早出现的 MMC 是由半桥子模块（Half Bridge Sub-Module,HBSM）串联而成，由于HBSM 结构简单，现有的MMC 直流输电工程均采用HBSM 结构。为了隔离直流故障时的短路电流，出现了全桥子模块（Full-Bridge Sub-Module,FBSM），但FBSM 的成本几乎是HBSM 的2 倍。为了同时隔离直流短路电流并降低成本，Marquardt提出了钳位双子模块（Clamp Double Sub-Module,CDSM）结构[1,2]，如图1 所示。

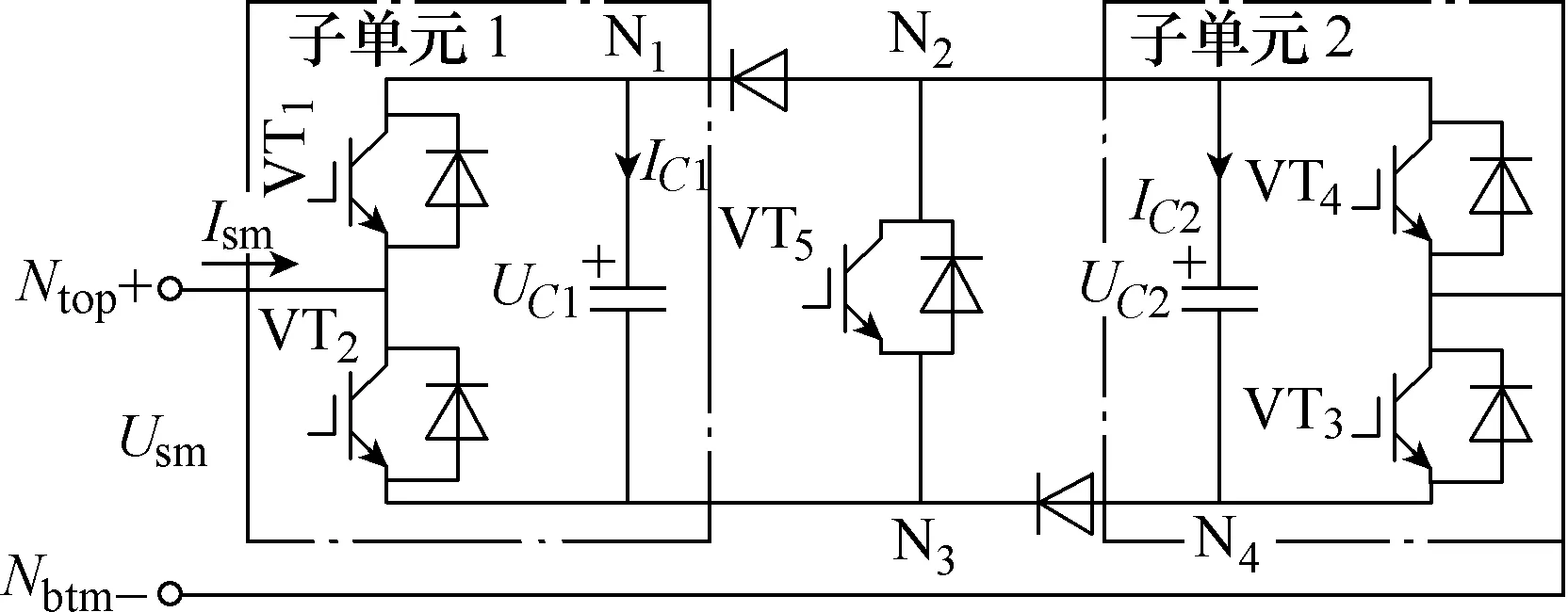
图1 CDSM 拓扑结构Fig.1 Topology of CDSM

受限于开关器件的性能，高压大容量的MMC通过提高电平数来提高电压等级和输电容量，导致子模块数目特别庞大。在PSCAD/EMTDC 中，对大规模CDSM-MMC 系统，使用器件搭建模型进行仿真时，不仅模型搭建困难，而且仿真效率极低。在配置CPU 为i5、内存8GB 的计算机上，使用PSCAD搭建上百电平CDSM-MMC 系统，仿真耗时达数天之久，严重影响了模型调试以及其他后续研究。

为解决仿真的规模问题，学者们针对HBSM 结构的MMC 提出了电磁暂态高效仿真模型。文献[3]基于节点电压法，将原有MMC 模型中超大规模矩阵分割成小矩阵，以提升仿真速率。但这种模型对闭锁状态的一些特定条件具有局限性[4]，并且该方案采用等效电流源和电压源的接入方式，在电磁暂态仿真过程中会造成一个仿真步长的滞后，在一定程序上降低了仿真精度。文献[5]使用基于嵌套的快速同步解决方案[4]提出了等效模型，通过诺顿等效，将原有多节点的桥臂模型等效为 2 节点的等效电路。这种方法虽然增加了得出等效电路的时间，但大幅度减少了整体网络矩阵的维度，从而减少了仿真时间。但是文献[5]并未解决在闭锁状态的问题，为此文献[6]利用PSCAD 自带的二极管器件来解决闭锁状态，提升模型在闭锁状态中的准确度。上述模型的仿真时间都会随子模块个数的增加而增加。针对这个问题，文献[7]提出了一种更为高效的模型，即对桥臂模型进一步简化，假设桥臂中的所有电容电压保持不变，直接利用调制比对桥臂进行控制。此模型的仿真时间不会随子模块个数的增加而增加，大幅度地提升了仿真速率。

本文分析了 CDSM 的工作特性，结合传统HBSM 的电磁暂态高效仿真模型建模的方法，提出了适合于 CDSM 仿真的两种高效电磁暂态仿真模型:基于戴维南定理的等效模型和基于平均等效的开关信号模型。其中，为了提高闭锁状态下的仿真精度，设计了级联子模块的等值仿真拓扑。最后，在PSCAD/EMTDC 中搭建了传统模型和本文提出的两种模型。通过仿真证明了两种模型的仿真精度和计算效率。

1 CDSM 拓扑结构及工作特性

CDSM 利用三个二极管和一个IGBT 将两个子单元连接起来（见图1），每个子单元本质上等同于一个半桥子模块。在子单元中，由于反相并联二极管的存在，其电容电压始终保持为非负。在正常工作状态下，VT5触发，此时N2和N3之间导通，N1和N2之间断开，N3和N4之间断开，CDSM 可等效为两个半桥子模块的级联，工作特性与半桥子模块相同。相应地，通过IGBT 控制CDSM，其外电压呈现0、UC和2UC三种模式。在闭锁状态下，所有IGBT 闭锁，由于二极管的正向导通性，根据电流方向的不同呈现不同的电压输出外特性。当电压Usm为正时，电流在CDSM 的通路如图2a 箭头所示，两个电容等效为串联充电，子模块输出电压为2UC；当电压Usm为负时，电容反向并联充电，子模块输出电压为-UC，如图2b 所示。

图2 CDSM 闭锁状态Fig.2 Blocked state of CDSM

在直流侧发生故障时，桥臂上所有CDSM 闭锁。含有N 个级联CDSM 的桥臂提供至少为NUC的反向电动势。由于通常的NUC≈Udc＞2Um，交流系统和直流侧故障点无法形成电流回路，实现直流侧故障的自清除[2,8]。其中，Udc为直流侧电压，Um为交流侧相电压幅值。

2 CDSM 等效模型

2.1 子模块正常状态等值

在电磁暂态模型中，依据Dommel 电磁暂态计算原理，电容可等值为 UCeq(t-Δt)的受控电压源和电阻RC[9]。使用梯形积分法时，其计算式为

式中，C 为电容；Δt 为积分步长。

二极管或者IGBT 等开关器件可等值为ON/OFF的可变电阻，器件导通时，阻值为RON（一般为mΩ级）；器件关断时，阻值为ROFF（一般为MΩ级）。因而，一个CDSM 在电磁暂态程序中可以等值为如图3a 所示的电路。

图3 CDSM 正常状态的等效电路Fig.3 Equivalent circuits of CDSM under normal state

在正常工作状态下，RD电阻为RON，RD1和RD2电阻都为ROFF，假定二极管RD1和RD2的关断电阻ROFF趋于无穷大，则一个CDSM 可简化为如图3b所示的等效电路，相当于两个子单元的串联。进一步对子单元进行化简，将其等效为图3c 所示的戴维南等效电路，其中Reqx和Ueqx分别为

式中，x 表示子单元编号。

2.2 子模块闭锁状态等值

在闭锁状态下，所有IGBT 关断，子模块中只存在二极管器件。在定步长的电磁暂态仿真程序中，需要对二极管进行插值计算，以正确模拟二极管的单向导通特性。由于PSCAD/EMTDC 软件并不提供插值算法的对外接口，在用户使用自定义模块进行编程时，无法有效地使用插值算法对二极管进行等效。

为此，采用PSCAD/EMTDC 中自带二极管函数进行模拟。同样地，需要对电容进行等值，闭锁状态子模块等效电路如图4 所示。

图4 CDSM 闭锁状态的等效电路Fig.4 Equivalent circuit of CDSM under blocked state

2.3 闭锁状态与正常状态的切换

通过前面的等值分析，在正常状态下，桥臂中子单元1 和子单元2 可化简为两个戴维南电路，类似于图3c，等效电阻和电源为

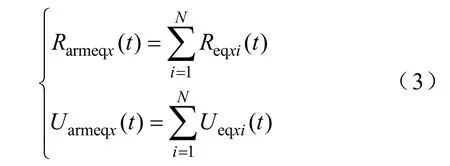
式中，i 表示桥臂中子模块编号。

考虑控制器的作用，只有处于投入状态的CDSM 子单元参与运行，CDSM 等效模型的桥臂等效电路如图5 所示。

图5 CDSM 等效模型的桥臂等效电路Fig.5 Detailed equivalent model of CDSM

图5 中，加入的三个IGBT 器件用以实现闭锁与正常状态的切换。在闭锁状态时，IGBT 的触发信号EN 为0，所有子单元的控制信号强制为1，每个子单元相当于电容。在正常状态下，EN 触发信号为1，由于电容电压不可能为负，其中电路通路如图5 中的虚线所示，所有子单元的控制信号由外部控制器给定。

2.4 实现流程

图6 等效模型实现示意图Fig.6 Schematic diagram of equivalent model

图6 为等效模型在PSCAD/EMTDC 中的实现示意图。点划线框中是桥臂等效模型，包括两部分:等效电路和等值计算。将等效电路输入EMTDC 程序用于网络求解。在EMTDC 网络求解之前，等值计算主要根据控制信号和子模块上一时刻状态进行等值化简，得到等效电路的参数；在EMTDC 网络求解之后，等值计算根据求解得到的当前时刻桥臂电流反向求取原有桥臂的电容电压和电流，计算式如式（4）所示。等效计算的流程如图7 所示。

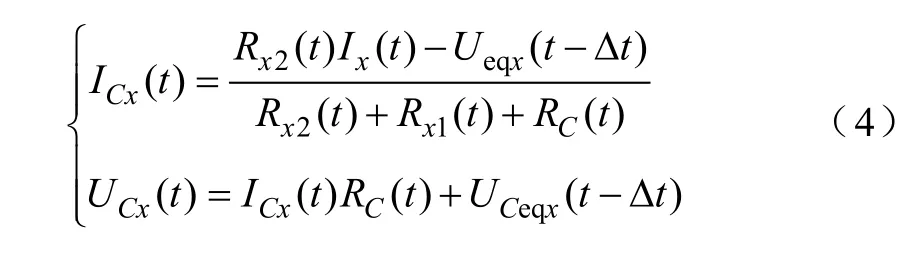
图7 等效模型实现过程Fig.7 Calculation flow chart of equivalent model

3 CDSM 开关信号模型

3.1 开关信号等效

单个子单元输出电压、电流与电容电压、电流的关系为[10]式中，Six为子单元的0/1 开关信号。式（5）中可以采用受控电压源和电流源来表示子单元，如图 8所示。

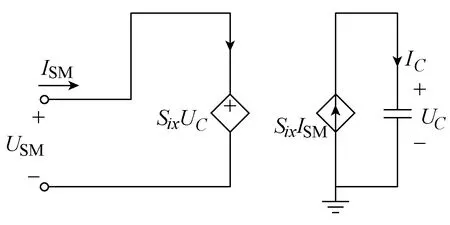
图8 子单元等效模型Fig.8 Equivalent model of sub-element

在满足一定仿真精度下，为了进一步提高CDSM 模型的仿真效率，对CDSM 进行简化。假设电容为理想均压，即桥臂中的电容电压能始终保持相等。则原有桥臂等值模型的两个戴维南电路可以用子单元等效模型替代，如图9 所示，其中的受控电压源通过式（6）计算所得，等值电容电压为Ceq=2NCSM。

图9 开关信号模型的桥臂等效电路Fig.9 Switch signal model of bridge arm equiralent circuit

3.2 实现过程

开关信号模型的实现过程与等效模型类似，其等效电路图9 所示。在EMTDC 网络求解前，等值计算只需要通过等效开关信号计算受控源的数值，网络求解之后则采集桥臂等效电容电压，实际子模块的电容电压为

在调制策略为最近电平逼近调制时，只需要使用最近电平调制输出的桥臂投入子单元个数来计算等效开关信号，即SN=NON/(2N)。

4 仿真

为了证明本文模型的仿真精度和效率，在PSCAD/EMTDC 中搭建了CDSM 桥臂传统模型，并将其中的桥臂模型替换为等效模型或开关信号模型。搭建的模型以及参数如图10 所示。在PSCAD中使用Fortran 代码编写了自定义的等效模型和开关信号模型。模型的仿真步长为20μs，画图步长为500μs。

图10 仿真系统模型及参数Fig.10 Model and parameters of simulation system

4.1 仿真精度

4.1.1 稳态运行

稳态运行时，交流侧与直流侧传输的有功功率为100MW。图11 为A 相上桥臂电流、电容电压和A 相交流侧电流的对比波形，可以看出，三种模型在桥臂的外特性上几乎一致。定义与传统模型之间误差绝对值归一化后的结果为等效模型的误差。计算得到等效模型和开关函数模型对应的子模块电容电压的误差分别为0.048%和0.151%。可见在稳态状态下，两种等效模型的仿真精度均较高。

4.1.2 交流侧故障

图12 为在2s 发生交流侧A 相接地故障、持续时间为0.05s 的仿真波形对比，由图可知，三种模型的换流站外特性保持高度一致。以交流侧A 相电流来计算两种等效模型的误差，等效模型误差为1.93%，开关信号模型误差为1.96%。

图11 稳态仿真波形对比Fig.11 Comparison of simulation waveforms under steady state

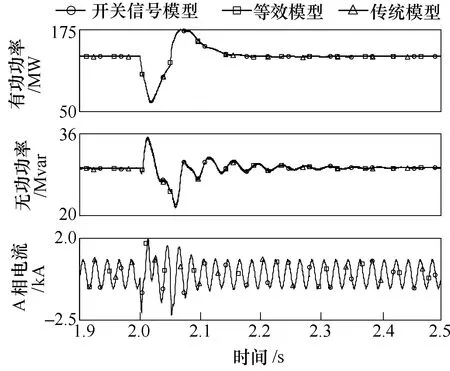
图12 交流侧故障仿真波形对比Fig.12 Comparison of simulation waveforms with AC fault

4.1.3 直流侧故障

直流侧故障发生在2s，故障持续时间为0.05s，假定控制系统的动作延时为1ms，换流站闭锁。在故障结束后，换流站解除闭锁状态。图13 为直流侧仿真波形，由图可知，三种模型的波形基本一致。以子模块电容电压来计算误差，模型和开关函数模型的误差分别为0.37%和0.52%。

4.1.4 不控充电阶段

MMC 换流器在启动过程中需要对子模块中的电压进行充电[11]。图14 为不控充电阶段的仿真波形，可以看出，两种等效模型完全可以模拟闭锁状态。以直流侧电压波形来计算误差，等效模型和开关信号模型的误差分别为0.54%和0.89%。

图13 直流侧故障仿真波形对比Fig.13 Comparison of simulation waveforms with DC fault

图14 不控充电阶段仿真波形对比Fig.14 Comparison of simulation results under uncontrolled charge state

4.2 仿真速率对比

为了减少因控制系统以及其他因素对仿真速率的影响，本文搭建了单桥臂仿真模型。其中控制系统触发信号由PWM 产生，每个子单元的载波相差π/N，仿真时间为5s。

表1 为仿真时间对比，可明显看出，与传统模型相比，等效模型和开关信号模型都具有高仿真效率。在含有五个子模块（相当于11 电平）的桥臂仿真中，相对等效模型，开关信号模型并不具有优势，主要是因为开关信号模型的节点数比等效模型多，因网络矩阵维度增加的耗时大于因桥臂等值计算的耗时。随着子模块数的增加，开关信号模型与等效模型相比，耗时更短。

表1 单桥臂模型仿真时间对比Tab.1 Simulation time comparison of single bridge arm models

4.3 模型分析

文中等效模型建立的过程中，都有不同程度的简化和假设。两种模型简化过程中只考虑了正常运行状态和闭锁状态，并未考虑故障状态（如电容击穿、IGBT 拒动）。为了仿真内部故障，可将传统模型的子模块和等效模型串联作为桥臂。子模块故障设置在传统模型的子模块中，以反映子模块内部的故障情况。开关信号模型输出的电容电压相当于桥臂中电容电压的平均值，无法有效地仿真桥臂内部特性。CDSM-MMC 的电平数高时，电压均衡控制算法占有计算资源大[12]。而使用开关函数模型时，控制模型中无需搭建电容电压均压控制部分，可以进一步提高仿真效率。

因此，等效模型适合于考虑换流站内部特性的CDSM-MMC 快速仿真建模中；而开关信号模型则更适合于含大规模 CDSM-MMC 的交直流混合仿真中。

5 结论

本文针对CDSM-MMC 的特性，在PSCAD 中建立了两种适合大规模CDSM-MMC 仿真的高效模型:等效模型和开关信号模型。

1）等效模型，仿真精度高，适合于含有完整控制系统的CDSM-MMC 系统仿真。可以通过与传统模型混合串联，对子模块内部故障进行仿真。

2）开关信号模型，仿真精度较高，适合于研究CDSM 外特性，能完整反映换流站的外部特性及内部的环流特性。该模型无法模拟子模块的均压特性。

3）相对于传统模型，两种模型都具有较高的仿真效率。

[1]薛英林,徐政.C-MMC 直流故障穿越机理及改进拓扑方案[J].中国电机工程学报,2013,33(21):63-70.Xue Yinglin,Xu Zheng.DC fault ride-through mechanism and improved topology scheme of C-MMC[J].Proceedings of the CSEE,2013,33(21):63-70.

[2]丁云芝,苏建徽,周建.基于钳位双子模块的MMC 故障清除和重启能力分析[J].电力系统自动化,2014,38(1):97-103.Ding Yunzhi,Su Jianhui,Zhou Jian.Analysis on fault current limitation and self-recovery of MMC base on clamp double sub-module[J].Automation of Electric Power System,2014,38(1):97-103.

[3]徐建中,赵成勇,刘文静.超大规模MMC 电磁暂态仿真提速模型[J].中国电机工程学报,2013,33(20):114-120.Xu Jianzhong,Zhao Chengyong,Liu Wenjing.Accelerated model of ultra-large scale MMC in electromagnetic transient simulations[J].Proceedings of the CSEE,2013,33(20):114-120.

[4]Beddard A,Barnes M,Preese R.Comparison of detailed modeling techniques for MMC employed on VSC-HVDC schemes[J].IEEE Transactions on Power Delivery,2015,30(2):579-589.

[5]Ganarathna U N,Gole A M,Jayasinghe R P.Efficient modeling of modular multilevel HVDC converter(MMC) on electromagnetic transient simulation programs[J].IEEE Transactions on Power Delivery,2011,26(1):316-324.

[6]唐庚,徐政,刘昇.改进式模块化多电平换流器快速仿真方法[J].电力系统自动化,2014,38(24):56-62.Tang Geng,Xu Zheng,Liu Sheng.Improved fast model of the modular multilevel converter[J].Automation of Electric Power System,2014,38(24):56-62.

[7]郭高朋,胡学浩,温家良,等.基于大规模子模块群的 MMC 建模与快速仿真算法[J].电网技术,2015,39(5):1226-1232.Guo Gaopeng,Hu Xuehao,Wen Jialiang,et al.A large-scale submodule group based algorithm for modeling and high-speed simulation of modular multilevel converter[J].Power System Technology,2015,39(5):1226-1232.

[8]张建坡,赵成勇,孙海峰,等.模块化多电平换流器改进拓扑结构及其应用[J].电工技术学报,2014,29(8):173-179.Zhang Jianpo,Zhao Chengyong,Sun Haifeng,et al.Improve topology of modular multilevel converter and application[J].Transactions of China Electrotechnical Society,2014,29(8):173-179.

[9]杨煜,孙大卫,谢小荣,等.模块化多电平换流器型柔性直流系统的等效仿真方法比较[J].电力系统保护与控制,2015,43(12):43-48.Yang Yu,Sun Dawei,Xie Xiaorong,et al.Comparative study on the accelerated models of MMC-based VSC-HVDC systems[J].Power System Protection and Control,2015,43(12):43-48.

[10]Saad H,Dennetière S,Mahseredjian J,et al.Modular multilevel converter models for electeomagnetic transients[J].IEEE Transactions on Power Delivery,2014,29(3):1481-1489.

[11]罗雨,饶宏,许树楷,等.级联多电平换流器的高效仿真模型[J].中国电机工程学报,2014,34(15):2346-2352.Luo Yu,Rao Hong,Xu Shukai,et al.Efficient modeling for cascading multilevel converter[J].Proceedings of the CSEE,2014,34(15):2346-2352.

[12]徐建中,赵成勇,Aniruddha M.Gole.模块化多电平换流器戴维南等效整体建模方法[J].中国电机工程学报,2015,35(18):1919-1929.Xu Jianzhong,Zhao Chengyong,Aniruddha M G.Research on the Thévenin’s equivalent based integral modeling method of the modular multilevel converter(MMC)[J].Proceedings of the CSEE,2015,35(8):1919-1929.

[13]Yu Feng,Lin Weixing,Wang Xitian,et al.Fast voltage-balancing control and fast numerical simulation model for the modular multilevel converter[J].IEEE Transactions on Power Delivery,2015,30(1):220-228.