单绕组磁悬浮开关磁阻飞轮电机和声混沌搜索优化设计

袁 野 孙玉坤 黄永红 周云红

（1.江苏大学电气信息工程学院 镇江 212013 2.南京工程学院电力工程学院 南京 211167）

1 引言

飞轮储能[1-3]技术被认为是近期最有希望和最有竟争力的新型能量储存技术，受到国内外专家的一致重视。作为一种将电能转化为机械能进行存储的装置，电机的运行状态直接决定整个飞轮系统的储能情况，是实现飞轮超高速运行的首要条件。开关磁阻电动机[4,5]具有结构简单、造价低廉、机体坚固、可靠性高、调速范围广以及相对较高的转矩质量比等优点，在飞轮储能中的应用受到青睐。磁悬浮开关磁阻电机[6-9]结合磁轴承与开关磁阻电机优点，可实现超高速、大功率运行。

通过对物理、自然或社会现象的观察和模拟，人们成功地提出了以模拟退火、遗传算法和禁忌搜索等为代表的新型电机优化设计方法[10-12]。模拟退火算法具有较好搜索能力，搜索过程可以避免陷入局部最优解。缺点是对整个搜索空间了解不多，不便于使搜索过程进入最有希望的搜索区域，导致采样次数多，优化时间长。遗传算法是一种高度并行、随机和自适应的算法，全局搜索能力强，缺点是局部搜索能力较弱。禁忌搜索算法避免寻优过程中大量无效劳动，但是条件判断方面不够成熟。本文采用和声混沌搜索（Harmony Chaotic Search，HCS）参数优化方法，初步设计出更适合应用于飞轮储能的单绕组磁悬浮开关磁阻飞轮电机（SWBSRFM）。由于电机采用外转子结构，转子可以直接驱动飞轮，减少了装置轴向长度，结构更加紧凑，且每一定子极上仅有一套绕组，每套绕组独立控制，省去了额外的悬浮力控制绕组，所以成本更低，维护更加方便。通过有限元仿真分析飞轮电机电磁性能，针对电机参数优化设计问题，通过数据分析和仿真实验，验证了所述HCS 优化方法简单、快速、精确，且优化后的电机具有良好悬浮和电磁转矩性能。

2 SWBSRFM 基本原理与主体尺寸

将开关磁阻电机定、转子结构互换，转子直驱飞轮，省去机械传动装置，结构紧凑，更适合应用于飞轮储能系统。SWBSRFM 的结构示意图如图1所示。使用的电机模型为三相12/8 极结构，定子极数12，转子极数8。共有三相，A 相绕组由A1～A4组成，B 相和C 相绕组沿A 相绕组逆时针方向30°和60°放置。每个定子极上仅有一套绕组，每套绕组匝数均为N，通过控制绕组中电流转矩分量和悬浮力分量维持转子稳定运行。Dr为转子外径，Ds为SWBSRFM 的定子内径，hcr，hcs分别为SWBSRFM转子轭高和定子轭高。根据电机设计经验，定子转子极弧宽均为α，考虑到装配难度，定转子气隙σ 定为0.5mm。

本文所提SWBSRFM 与传统磁悬浮开关磁阻电机[13]（BRSM）用两套绕组分别产生转矩磁场和悬浮磁场不同，SWBSRFM 的转矩磁场和悬浮磁场仅由一套定子绕组产生。因此在单绕组结构中可将每极定子绕组电流等效为转矩分量和悬浮分量之和。例如A 相每极绕组电流iA1～iA4与电流转矩分量ima、电流悬浮分量isa1、isa2存在式（1）的函数关系。

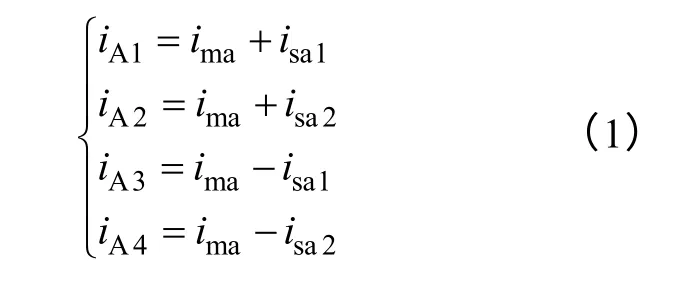
SWBSRFM 定、转子极弧选取是以同时提升转矩和悬浮力指标为优化目的，即不仅要保证转矩的输出，也要满足径向悬浮力要求。为保证电机正反两方向的起动，其定、转子极弧角应满足下式

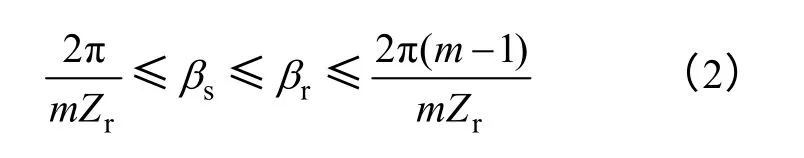
式中，m 为电机相数；Zr为转子齿数；αs和αr分别为定转子极弧宽。

电机转子角度的零度定义在定子齿轴线与凸极转子齿轴线的重合位置。该位置处的电感量最大，径向力也最大，旋转力最小。

图2 中假设：①忽略磁饱和；②转子轴心偏移与气隙长度相比很小；③忽略漏磁通；④转子转角顺时针为正；⑤定、转子极中心线对齐的位置为转子零度位置；⑥在转子零度位置忽略边缘磁通；⑦各相绕组轮流导通工作。获得A 相绕组的等效磁路，如图2 所示，其中N 为每极绕组的匝数，ia1～ia4分别为A 相4 极绕组的电流，φa1～φa4分别为A相四个气隙下的磁通，Pa1～Pa4为A 相绕组每个齿极下的气隙磁导。结合文献[13]详细推导出电机的气隙磁导Pa1～Pa4。设定转子处于几何位置中心，无径向位移。结合前文BSRM 数学模型的推导方法，考虑到因槽口影响使气隙磁阻增加而引入的系数，一个磁极下的气隙磁导为

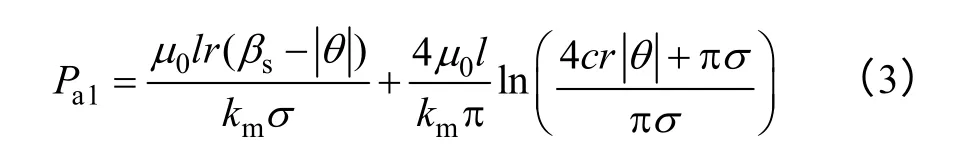
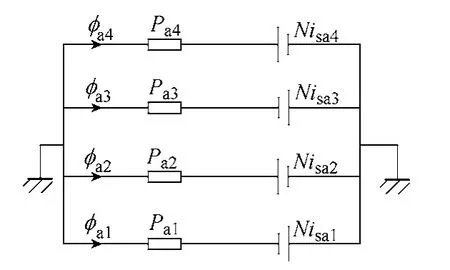
图2 A 相绕组等效磁路Fig.2 Equivalent circuit of A phase

式中，l 为电机的轴向有效长度；θ 为转子齿极与定子齿极之间的夹角（一般约定转子齿极于定子齿极对齐时为0°，且转子逆时针旋转）；r 为SWBSRFM 定子半径，c≈1.49。

利用电感与磁链的函数关系，得到自感和互感为

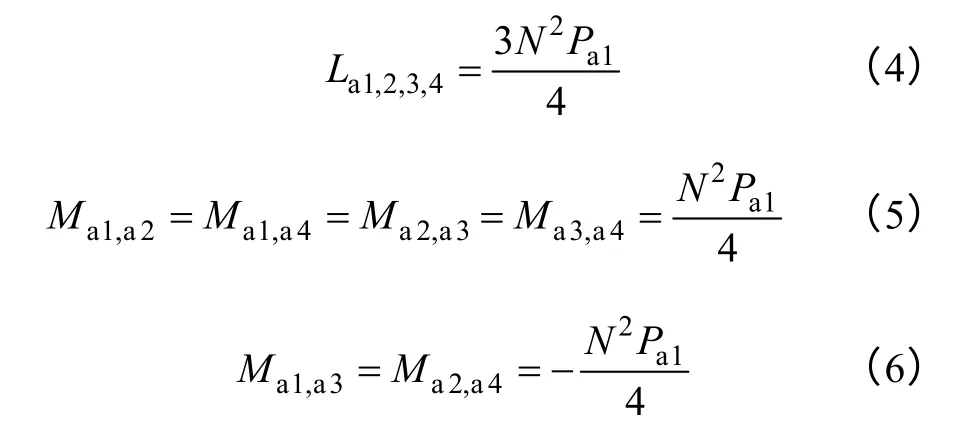
单绕组磁悬浮开关磁阻电机的一般采用单相绕组导通控制策略，三相依次导通，且兼具旋转与悬浮，电机的磁场储能可由A 相绕组励磁产生的磁场储能来表示

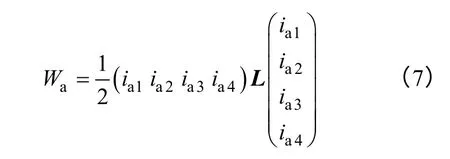
将控制电流等效于转矩电流和悬浮电流

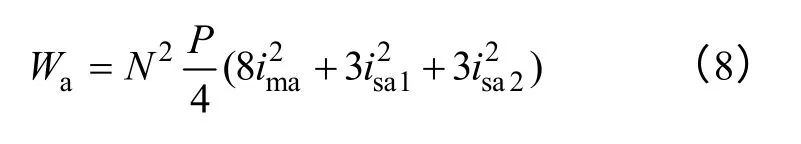
对式（8）在一个周期内积分并取平均，则电机输出平均转矩为

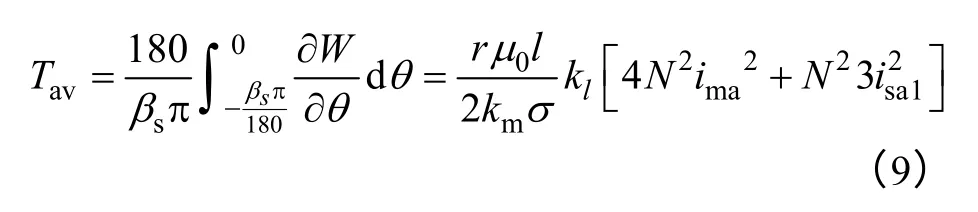
A 相平均转矩还可以表示为

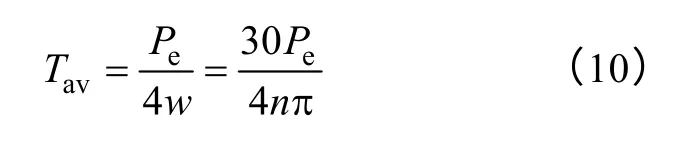
式中，Pe为电磁功率；w 为角速度；n 为电机转速。得到飞轮电机定子外径表达式为

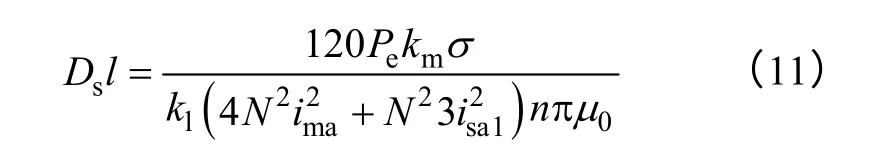
在电机中，沿电枢圆周方向气隙磁场不是均匀分布的。为了计算方便，定义B 为电机转子与定子凸极齿对齐时，最大气隙磁通密度，可由硅钢片型号以及结构确定。为了保证在悬浮力满足基本设计要求情况下，电机能产生稳定的转矩，一般等效主绕组磁动势需大于悬浮绕组磁动势

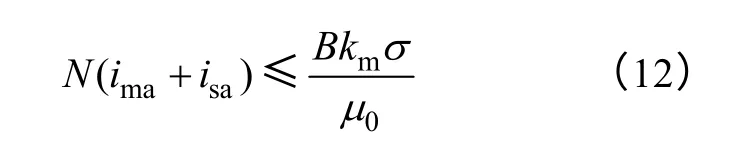
结合式（11）和式（12）可以得到单绕组磁悬浮飞轮电机主体尺寸为

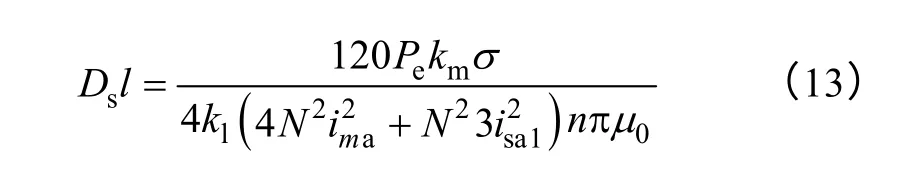
由于铁心结构相同，SWBSRFM 定转子基本尺寸设计方法可以借鉴开关磁阻电机基本尺寸[14]设计方法。图3 为飞轮装置结构图。

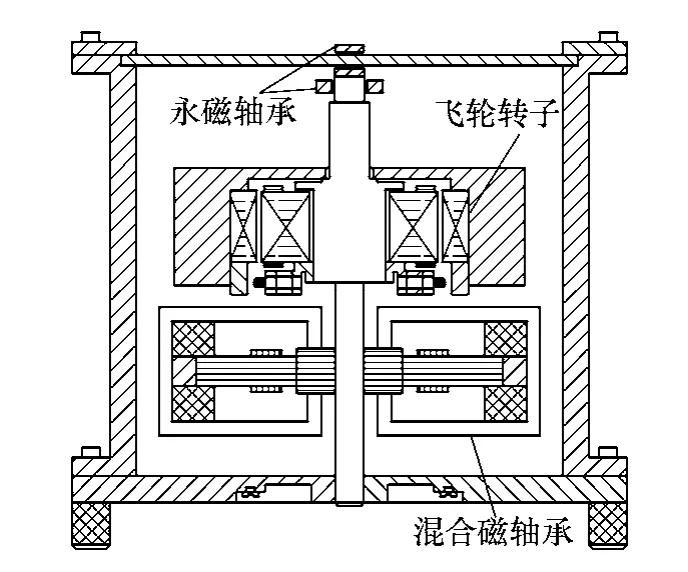
图3 飞轮装置结构Fig.3 The structure of flywheel device

3 单绕组磁悬浮开关磁阻飞轮电机和声混沌搜索优化设计

和声搜索[14-16]（Harmony Search，HS）是一种新的启发式优化算法。算法模拟了音乐创作中乐师们凭借记忆，通过反复调整乐队中各乐器的音调，最终达到一个美妙的和声状态的过程。每个音乐演奏者对应每个决策变量xi（i=1，2，3，…，n），决策变量的个数即为和声库（Harmony Memory Size，HMS）大小。每个乐器的音高对应每个决策变量的值域，xi～[xiu，xil]，其中xiu与xil为对应的决策变量的最大值和最小值，n 个决策变量值可组成一组解向量。和声品质通过一次次的实践得到提高，在工程优化中，每一个决策变量在可行域中任选一个值合成一个解向量，根据目标函数值判断，如果此为较好的方案，则被保存。

和声算法引入两个参数：记忆库取值概率（Harmony Memory Considering Rate，HMCR）和微调概率（Pitch Adjusting Rate，PAR）。其具体的含义为：在0～1 内随机选取一个数random（0,1）。

（1）当random（0,1）＜HMCR 时，在HMS 中随机选取一组解向量。

（2）当random（0,1）＞HMCR 时，在决策变量值域内搜索解向量。对于选取的解向量，需要通过PAR 来判断是否进行局部微调。最后根据新的解向量判断目标函数值是否优于HMS 内的最差解，若是，则更新和声库，并不断迭代，直至达到预定迭代次数。

混沌具有精致的内在结构，能把系统的运动吸引在特定范围内。混沌运动具有很强的随机性、遍历性和规律性，利用混沌变量的遍历性对解空间探索是一种可行方案。常用Logistic 映射来更新混沌变量的值。

结合混沌搜索[17,18]（Chaotic Search,CS）的全局历遍性与和声搜索简单、灵活的优点，得到和声混沌搜索算法以在较短的时间内获取电机的最优结构参数。图4 为和声混沌算法的大致流程图。具体步骤如下：

Step1：初始化混沌和声搜索算法参数，HCS最大迭代次数Imax，CS 最小迭代次Cmin，最大迭代次数Cmax，混沌搜索所需迭代次数Cnow，和声决策变量值域以及和声库数据。

Step2：和声搜索。判断random（0,1）与HMCR的大小，以确定解向量在和声库内随机产生还是在决策变量值域内随机产生。再通过random（0,1）与PAR 大小关系，决定是否对解向量进行扰动，若是，扰动范围由参数bw 决定。

Step3：若所得解向量的目标函数值优于和声库中的“最差和声”，则取代和声库中最差和声，否则不操作。

Step4：找出此时和声库中的最优和声，设定为混沌搜索初值f1，比较此和声若与之前迭代产生的和声相同则跳过混沌搜索，回到步骤Step2，否则进行混沌搜索。

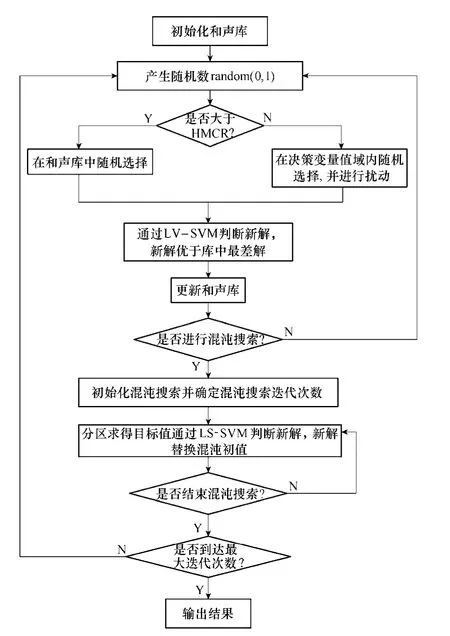
图4 电机结构参数HCS 优化流程图Fig.4 Flow chart of parameters optimization with HCS

Step4.1：混沌搜索，通过下式得出混沌搜索的迭代次数

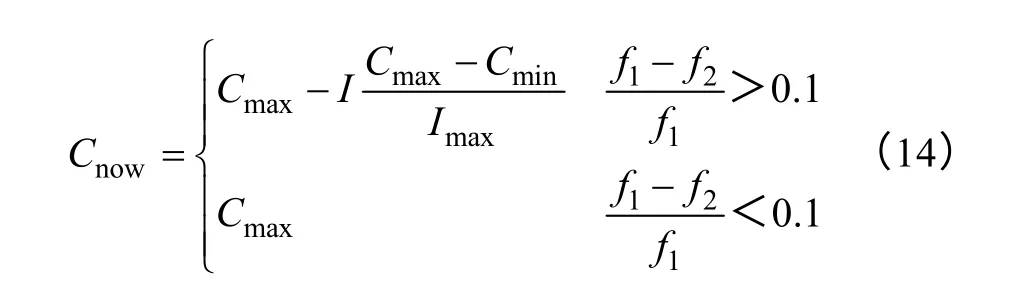
式中，f1为此时和声库最优声；f2为此前迭代产生的和声。

Step4.2：将和声变量区间划分为三个小区间，分别得到混沌变量，使得～(0,1)。其中k=0，1，2，…，Cnow；l=1，2，3。每个区间最大值与最小值为Ul，Ll。 k

lr 可由式（3）计算得到

Step4.3：利用Logistic 映射来产生新的混沌变量

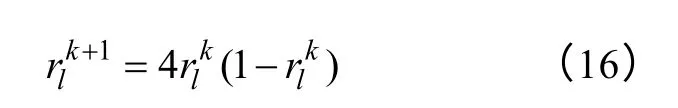
根据式（3）得到三个新的解向量lx′，求得此时三个目标函数值lf′，并与f1比较。若lf′优于f1，则替换，否则不替换。重复操作Step4.3，直到混沌搜索的迭代次数。

Step 5：回到Step2 直至最大迭代次数。

4 单绕组磁悬浮开关磁阻飞轮电机和声混沌搜索优化设计

4.1 SWBRSFM 电机优化参数与优化目标

实验室样机设计目标：额定功率3kW 左右，额定电压110V，额定转速10 000r/min，效率不小于75%。Ansoft 有限元仿真时间为电机A1绕组所在定子齿与转子齿重合位置到两者恰好不重合位置，为了便于对比最终优化结果，做如下统一规定。

（1）A 相四极绕组的磁动势分别为

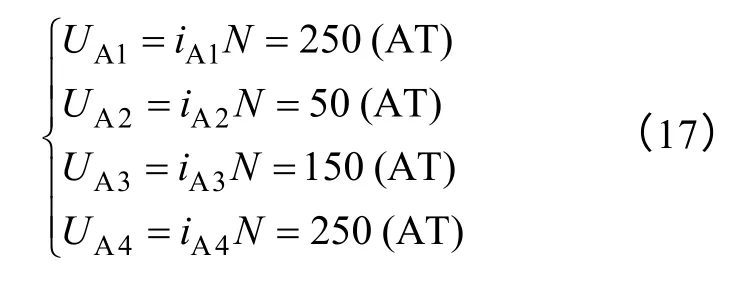
（2）不同极弧系数对应电机仿真时间均为1ms，需要在ansoft 软件内设置不同极弧宽对应转速设定公式为

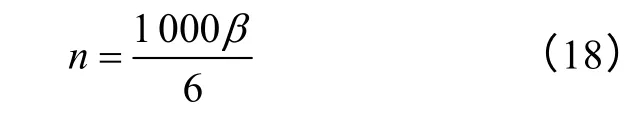
定义绕组产生的悬浮力为F，平均悬浮力为Favg，平均转矩为Tavg，转矩为T，电机铁心硅钢片体积为V，铜耗为P。则电机参数优化目标为性能指标转矩效率TP，悬浮效率FP，转矩功率密度TV，悬浮功率密度FV。其中

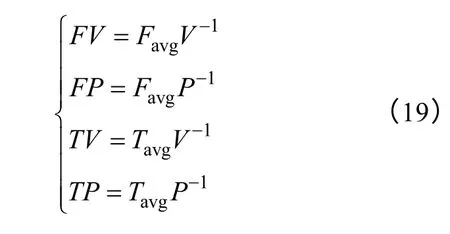
对于SWBSRFM，选取一相导通区间内的TP，FP，TV，和FV 作为性能评定参数。样机初始参数设为：Dr=130mm，l=40mm，σ=0.5mm，Da=37mm，以上变量均为不变参数，不在电机结构参数优化范围内。除不变参数外，参数有定子外径Ds，定转子极弧α，转子轭高hcr，定子轭高hcs以及绕组N。Ds=[96.5,98]，α=[15,16.5]，hcr=[9,10.5]，hcs=[9,10.5]，N=[32,38]，以上变量为考察参数。在理论上，不同结构参数组合对应不同TP、FP、TV、FV 值，原则上其值越大越好。但是由于参数众多，不能确定每组电机参数与TP、FP、TV、FV 之间的关系，因此采用单变量仿真分析上述参数对电机性能影响。

4.1.1 定子外径对电机性能影响

根据定子外径取值范围：Ds～[96.5mm,98mm]，取区间端点值作为参考变量，分析定子外径对电机性能影响。表1 给出了定子外径分别为96.5mm，98mm，其余考察参数不变时（α=15°，hcr=9.5mm，hcs=9.5mm，N=32），电机性能评定参数的取值情况。

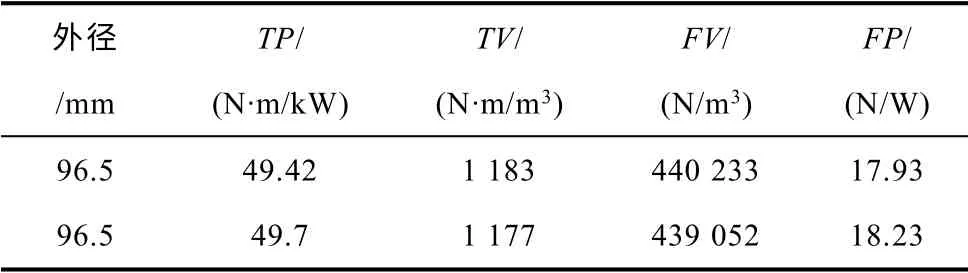
表1 定子外径对电机性能影响Tab.1 Influence of Ds for motor performance

由表1 可以看出：当定子外径为最小值（96.5 mm）时，TP、FV 与FP 小于定子外径为最大值（98mm）时的TP、FV 与FP，但是TV 却大于外径为最大值时的TV。表明电机性能指标参数取值在Ds～[96.5,98]非正比例增加，因此，Ds需要作为优化的结构参数。

4.1.2 转子（定子轭高）对电机性能影响

限于篇幅，只分析转子轭高对电机性能影响。表2 给出了轭高hcr分别为9mm 和10.5mm，其余考察参数不变（α=15°，Ds=96.5mm，hcs=9.5mm，N=32），电机性能评定参数的取值情况。

表2 转子轭高对电机性能影响Tab.2 Influence of hcr for motor performance

从表2 可以看出：当转子轭高为最小值（9mm）时，TV、FV 与FP 小于转子轭高为最大值（10.5mm）时的TV、FV 与FP，但是TP 却大于最大值时的TP。表明电机性能指标参数取值在hcr～[9,10.5]非正比例增加，因此，hcr需要作为优化的结构参数。

4.1.3 极弧对电机性能影响

表3 给出了极弧α分别为15°和16.5°，其余考察参数不变（hcr=10.5mm，Ds=96.5mm，hcs= 9.5mm，N=32），电机性能评定参数的取值情况。

表3 极弧对电机性能影响Tab.3 Influence of α for motor performance

从表3 可以看出：当极弧为最小值（15°）时，TP、TV 与FP 大于最大值（10.5mm）时的TP、TV 与FP，但是FV 却小于最大值时的FV。表明性能指标参数取值在α～[16.5,15]内非正比例增加，因此，α需要作为优化的结构参数。

4.1.4 绕组对电机性能影响。

表4 给出了绕组N 分别为32 和38，其余参数不变（hcr=10.5mm，Ds=96.5mm，hcs=9.5mm，α=15°），电机性能评定参数的取值情况。

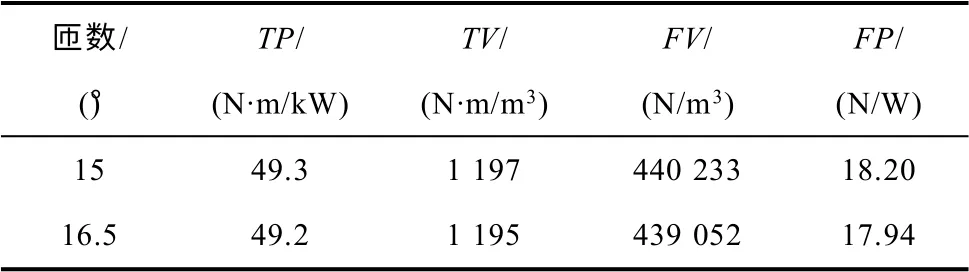
表4 绕组匝数对电机性能影响Tab.4 Influence of N for motor performance

从表4 可以看出：绕组匝数为32 匝时，电机性能指标参数值均大于绕组匝数为38 匝参数值，但参数值非常接近，误差在1%以内。为了使得结构参数在寻优过程中更加准确，本文将绕组匝数也作为电机结构参数优化目标。采用正交试验与随机试验设计方法，获得电机参数变量空间中有代表性的样本数据点，并建立最小二乘支持向量机[19,20]（LVSVM）非参数模型。SWBSRFM 考察结构参数因素和取值区间见表5。可优化参数初始值设置为Ds=96.5mm，α=15°，hcr=9mm，hcs=9mm，N =36。

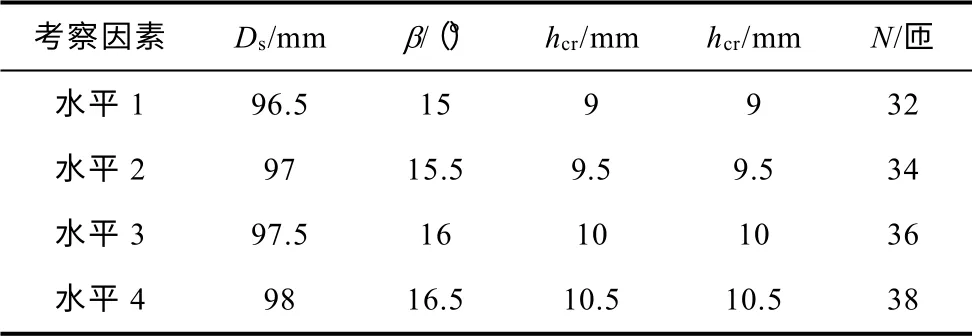
表5 SWBRSFM 结构参数因素水平表Tab.5 Level of the structural parameters of SWBRSFM

通过磁场仿真分析可知结构参数对TV、FV、FP 与TP 等优化目标的影响程度不同，将这些性能参数同时最大化作为优化目标函数将无法获得唯一最优解，因此必须重新设计优化目标函数。综合考虑电机性能参数与优化函数求解的唯一性，定义统一优化目标函数为

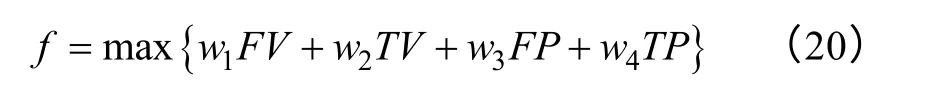
由于转子直驱飞轮，需提供足够大的悬浮力保证转子飞轮在恶劣环境下稳定悬浮。该飞轮装置在设计时，力求达到体积小，结构紧凑，悬浮性能好。因此参数FV 权重因子最大。同时考虑SWBSRFM的主要应用环境和飞轮装置设计要求，权重因子可以取：w1=0.4， w2=0.3，w3=0.2，w4=0.1。

4.2 和声混沌搜索策略参数设置

和声决策变量xi分别对应Ds、α、hcr、hcs、N。HMCR、PAR 和bw分别可由式（21）～式（23）得到。其中，Hmax=10 000，Hmin=7 000，Cmax=1 000，

Cmin= 800，Pmax=0.4，Pmin=0.3。

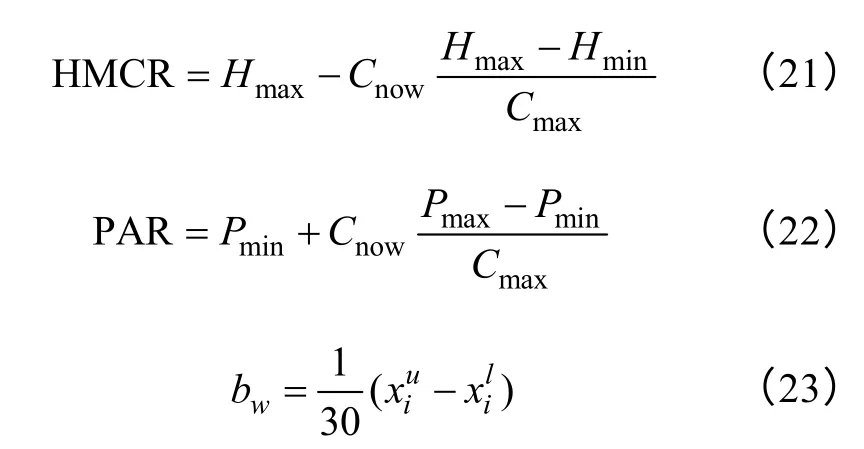
本实验中，通过正交试验得到的数据均放入和声库里，正交试验与随机试验得到的数据用来LVSVM 训练。

4.3 SWBRSFM 结构参数HCS 优化结果

表6 给出了用和声混沌搜索优化算法后的SWBRSFM 结构参数。表7 给出了初步设计样机（IDM）与优化后的SWBRSFM 转矩效率TP、悬浮效率FP、转矩功率密度TV 和悬浮功率密度FV性能比较。

表6 优化后SWBSRFM 参数Tab.6 Parameters of optimized SWBRSFM

表7 IDM 与优化后SWBSRFM 性能比较Tab.7 Performance comparison between optimized SWBRSFM and IDM

从实验数据可以看出：优化后的电机转矩效率TP 提高约1.9N·m/kW，悬浮效率FP 提高1.6F/W，转矩功率密度TV 提高45N·m/m3，悬浮功率密度FV提高25 948F/m3。各项性能指标均优于初始设计样机，表明单绕组磁悬浮飞轮电机，体积小，效率高，电磁特性优。在电机转子外径、定子内径、轴向长度以及轴向长度不变的条件下，定子外径、定转子极弧、转子轭高、定子轭高以及绕组作为可变参数，通过和声混沌搜索，结合统一优化目标函数，优化后电机的转矩效率TP、悬浮效率FP、转矩功率密度TV 和悬浮功率密度FV 均优于初始电机，表明和声混沌搜索基本满足电机参数优化设计要求。

为进一步验证优化后电机性能与和声混沌搜索算法的优越性，图5 给出了HCS 与HS 在寻求最优和声期间，目标函数值变化曲线。采样频率为500迭代次数。图6 与图7 给出优化后的SWBRSFM与相同尺寸下BRSM 转矩、水平方向悬浮力对比示意图。

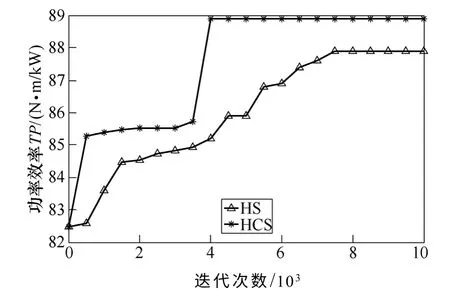
图5 目标函数值变化曲线Fig.5 Curve of objective function value

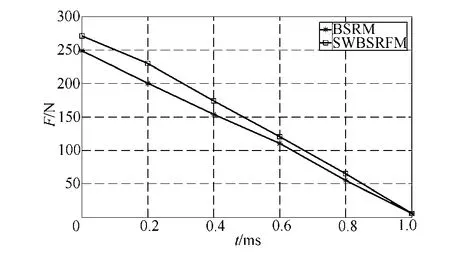
图6 SWBSRFM 与BSRM 水平悬浮力对比图Fig.6 Comparison chart of horizontal suspension force between SWBSRFM and BSRM

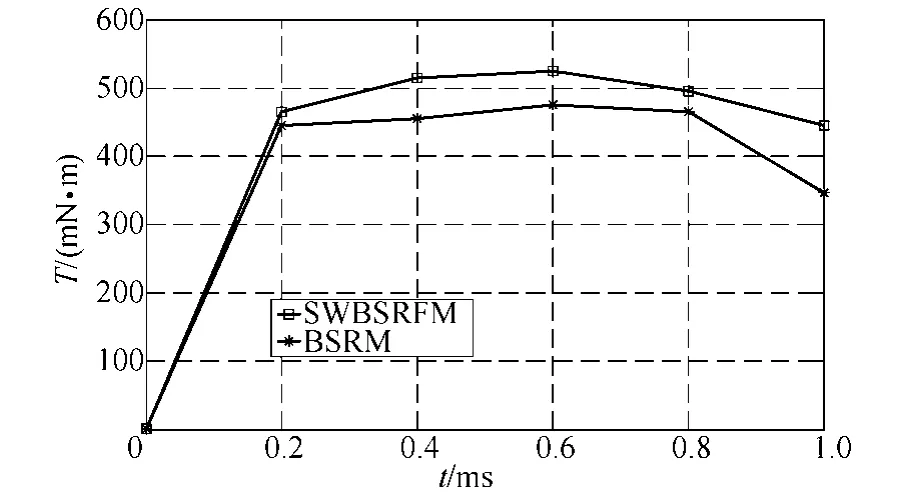
图7 SWBSRFM 与BSRM 转矩对比图Fig.7 Comparison chart of torque between SWBSRFM and BSRM

根据图5 所示，采用HCS 优化的SWBRSFM目标函数值在迭代4 000 次左右即可寻得最优和声，而采用HS，则78 000 次左右寻得“最优”和声，但所得目标函数值与采用HCS 优化相比，并没有达到最优效果。原因是HS 陷入了局部搜索，所得目标函数值仅是局部最优解。反映了混沌搜索全局历遍性可以弥补和声搜索局限性，同时HCS 又不失灵活、快速。

从图6 与图7 可以看出：

（1）采用HCS 优化后的SWBSRFM 转矩最大值0.51N·m，平均转矩约0.44N·m，均高于BSRM转矩最大值0.48N·m 平均转矩0.38N·m，优化后的电机具有良好的转矩特性。

（2）SWBSRFM 转矩降幅（导通区间内，转矩最大值与θ=15°时转矩值之差）约为0.05N·m，BSRM转矩降幅约0.14N·m，表明SWBSRFM 输出转矩更加稳定。

（3）SWBSRFM 最大悬浮力为270N，BSRM 最大悬浮力为250N，表明目标样机的悬浮能力优于相同外径下的BSRM。

（4）SWBSRFM 悬浮力在θ=0°与θ=15°分别取得最大值与最小值，且在导通区间内具有近似线性分布，符合磁悬浮开关磁阻电机基本的电磁特性，本文提出的SWBSRFM 设计方法具有一定可行性。

5 结论

现阶段，国内外对磁悬浮开关磁阻电机的研究尚处实验室阶段，仍有许多关键问题没有统一的解决方案。随着新型导电、导磁和绝缘材料以及优化算法的出现，从本体上对电机进行优化设计以加快磁悬浮开关磁阻电机普及应用，将是今后发展的一个重要方向。本文设计出更适合应用于飞轮储能的单绕组磁悬浮开关磁阻飞轮电机，将和声算法的简单、灵活特点与混沌变量的全局搜索能力结合起来，应用于样机结构参数优化。仿真试验表明：单绕组磁悬浮开关磁阻飞轮电机，体积小，效率高。通过和声混沌搜索优化，电机具有良好的转矩与悬浮能力。和声混沌搜索算法在参数优化过程中，精度高，速度快，为电机参数优化设计提供了新思路，同时适用于向其他工程领域推广应用。

[1] 张维煜,朱熀秋.飞轮储能关键技术及其发展现状[J].电工技术学报,2011,26(7):141-146.

Zhang Weiyu,Zhu Huangqiu.Key technologies and development status of flywheel energy storage system[J].Transactions of China Electrotechnical Society,2011,26(7):141-146.

[2] 王楠,李永丽,张玮亚,等.飞轮储能系统放电模式下的非线性控制算法[J].中国电机工程学报,2013,33(19):1-7.

Wang Nan,Li Yongli,Zhang Weiya,et al．A nonlinear control algorithm for flywheel energy storage systems in discharging mode[J].Proceedings of the CSEE,2013,33(19):1-7.

[3] 戴兴建,于涵,李奕良.飞轮储能系统充放电效率实验研究[J].电工技术学报,2009,24(3):20-24.

Dai Xingjian,Yu Han,Li Yiliang.Efficient test on the charging and discharging of the flywheel energy storage system[J].Transactions of China Electrotechnical Society,2009,24(3):20-24.

[4] 周强,刘闯,朱学忠,等.超高速开关磁阻电工机设计[J].中国电机工程学报,2009,29(9):89-92.

Zhou Qiang,Liu Chuang,Zhu Xuezhong,et al.Design of super high speed switched reluctance motor[J].Proceedings of the CSEE,2009,29(9):89-92.

[5] 郑洪涛,蒋静坪.开关磁阻电机高性能转矩控制策略研究[J].电工技术学报,2005,20(9):24-28.

Zheng Hongtao,Jiang Jingping.Study on high-grade torque control strategies for switched reluctance motor[J].Transactions of China Electrotechnical Society,2005,20(9):24-28.

[6] Takemoto M,Suzuki H,Chiba A,et al.Improved analysis of a bearingless switched reluctance motor[J].IEEE Transactions on Industry Applications,2001,37(1):26-34.

[7] Takemoto M,Chiba A,Akagi H,et al.Radial force and torque of a bearingless switched reluctance motor operating in a region of magnetic saturation[J].IEEE Transactions on Industry Applications,2004,40(1):103-112.

[8] Takemoto M,Chiba A,Fukao T.A new control method of bearingless switched reluctance motors using square-wave currents[C].Power Engineering Society Winter Meeting,Singapore,2000:375-380.

[9] Chen L,Hofmann W.Design procedure of bearingless high-speed switched reluctance motors[C].International Symposium on Power Electronics,Electrical Drives Automation and Motion,2010:1442-1447.

[10] 黄哲理,赵光,汪国梁.模拟退火法在电机全局优化设计中的应用研究[J].西安交通大学学报,1995,29(2):8-15.

Huang Zheli,Zhao Guang,Wang Guoliang.Applied research of the motor global optimization design based on simulated annealing[J].Journal of Xi’an Jiao Tong University,1995,29(2):8-15.

[11] 陈宇,卢琴芬,叶云岳.长定子同步直线电动机的设计及其优化[J].电工技术学报,2003,18(2):18-21.

Chen Yu,Lu Qinfen,Ye Yunyue.Optimal design of a long stator synchronous linear motor[J].Transactions of China Electrotechnical Society,2003,18(2):18-21.

[12] 贾克兵,孙昌治,耿连发.禁忌搜索算法在二相永磁同步电动机中的应用[J].微电机,2002,35(4):18-32.

Jia Kebing,Sun Changzhi,Geng Lianfa.The application of tabu algorithm to the optimization of twophase permanent magnet synchronous motor[J].Micromotors,2002,35(4):18-32.

[13] 孙玉坤,吴建兵,项倩雯.基于有限元法的磁悬浮开关磁阻电机数学模型[J].中国电机工程学报,2007,27(12):33-40.

Sun Yukun,Wu Jianbing,Xiang Qianwen.The mathematic model of bearingless switched reluctance motor based on the finite-element analysis[J].Proceedings of the CSEE,2007,27(12):33-40.

[14] Geem Z W,Kim J H,Loganathan G V.A new heurstic optimization algorithm:harmony search[J].Smiulation,2001,76(2):60-68.

[15] 刘蓓,汪沨,陈春.和声算法在含DG 配电网故障定位中的应用[J].电工技术学报,2013,28(5):280-284.

Liu Bei,Wang Feng,Chen Chun.Harmony search algorithm for solving fault location in distribution networks with DG[J].Transactions of China Electrotechnical Society,2013,28(5):280-284

[16] 宋志宇,李俊杰.和声搜索最小二乘支持向量机预测模型及其应用[J].哈尔滨工业大学学报,2009,41(8):207-210.

Song Zhiyu,Li Junjie.Prediction model based on least squares support vector machine with harmony search and its application[J].Journal of Harbin Institue of Technology,2009,41(8):207-210.

[17] 修春波,刘向东,张宇河.混沌优化与模糊控制在混沌控制中的应用[J].控制理论与应用,2005,22(1):63-66.

Xiu Chunbo,Liu Xiangdong,Zhang Yuhe.Applications of chaos optimization and fuzzy control in chaos control[J].Control Theory & Applications,2005,22(1):63-66.

[18] 罗钧,李研.具有混沌搜索策略的蜂群优化算法[J].控制与决策,2010,25(12):1913-1916.

Luo Jun,Li Yan.Artificial bee colony algorithm with chaotic-search strategy[J].Control and Decision,2010,25(12):1913-1916.

[19] Nurettin A.Classification of ECG beats by using a fast least square support vector machines with a dynamic programming feature selection algorithm[J].Neural Computing & Applications,2005,14(4):299-309.

[20] 贾嵘,王小宇,蔡振华.最小二乘支持向量机回归的HHT 在水轮发电机组故障诊断中的应用[J].中国电机工程学报,2006,26(22):128-133.

Jia Rong,Wang Xiaoyu,Cai Zhenhua.The hilbethuang transform based on least squares support regression machine and its application in the fault diagnosis of hydroelectric generation unit[J].Proceedings of the CSEE,2006,26(22):128-133.