基于遗传BP网络的城市空气质量等级预测

李世峰，邱占芝

(大连交通大学 机械工程学院，辽宁 大连 116028)*

0 引言

2013年，“雾霾”成为年度关键词，采用新空气质量标准的74个城市中，只有海口、舟山和拉萨3个城市达到了空气质量二级标准.2014年1月4日，国家减灾办、民政部首次将危害健康的雾霾天气纳入2013年自然灾情进行通报.空气质量的好坏及其对环境和民众健康的影响开始成为公众热议的话题.因此，对空气质量进行预测预报研究，对于防灾减灾以及公众健康都是十分重要的.

预测预报方法通常采用小波网络［1］、贝叶斯网络［2］等，利用遗传BP网络的预测预报方法一直是人们关注的研究课题.D.E.Rumelhat和J.L.McClelland在1986年提出了一种利用误差反向传播训练的神经网络，简称BP(Back Propagation)网络［3］.该算法具有较好的非线性映射能力，使得复杂问题能在很多中间过程未知情况下得到较合理的解答［4］.但典型的BP网络仍然存在过早收敛问题［5-6］，而且如何确定隐含层节点数目前尚无理论上的指导［7］，需要反复实验确定.遗传算法(Genetic Algorithm)具有并行计算、鲁棒性强等特点，特别适用于全局寻优问题.遗传BP网络融合了BP网络与遗传算法各自的优点，非常适合于建立预测模型，在股市预测［8］、电力负荷预测［9］、产品销售［10］、环境保护［11］等方面有着广泛的应用.本文尝试使用遗传BP网络，对城市空气质量等级进行预测.

1 神经网络的特点

神经网络仅仅依靠输入数据和输出数据就能完成网络的训练，学得蕴藏在输入数据与输出数据之间的模式，而不需要关心学习过程本身，极大的简化了对数据的处理过程，扩展了应用范围.但是神经网络预测有其局限性，并非所有的问题都可以用神经网络来进行预测.其中一类是完全随机的问题，如彩票，这类问题不能用神经网络来进行预测;另一类不可预测问题是无法获得输入信息，例如地震预测.

由于与空气质量等级相关的因素众多，我们并不知道该问题是否属于上述不可预测问题.在本案例中，我们尝试使用气象信息对空气质量等级进行预测，首先对数据进行了分析.网络预测输出为空气质量等级，共6类(优、良、轻、中、重、严重)，若输入输出之间为随机的，预测正确率17%(即1/6).在进行简易编码后使用典型BP网络对空气质量等级进行了预测，预测正确率在40%左右，40%的预测正确率在可预测问题里相对较低，BP网络应用于很多问题预测正确率可达70%以上，但该预测正确率仍远高于随机预测，足以证明的问题的可预测性.

2 数据预处理

2.1 文字属性编码

以大连市2013年10月28日开始的空气质量等级记录为例，选取大连市2013年11月 ～2014年4月(共181个样本)的天气记录及空气质量等级作为训练数据，预测未来数天的空气质量等级.输入信息如图1.

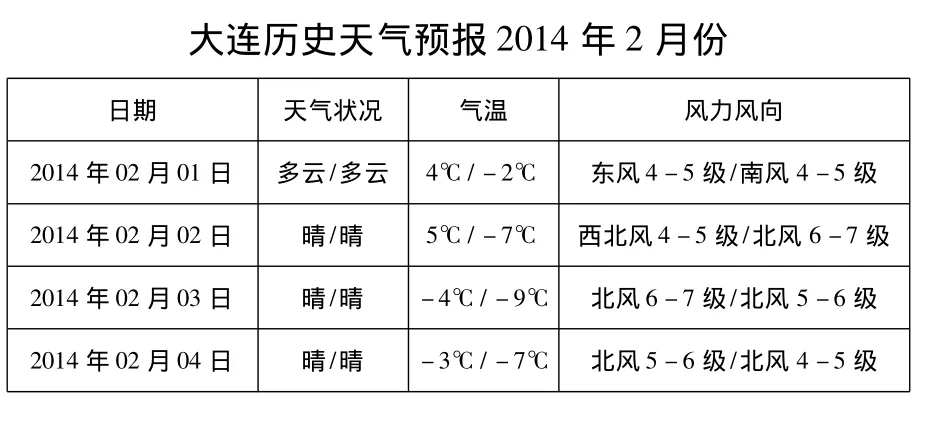
图1 气象信息截图

图中包含了大量的文字信息，依次为天气1、天气2、最高气温、最低气温、风向1、风力1、风向2、风力2.

众所周知，BP网络擅长处理数字问题，所以需要对文字信息进行编码.风向信息可依据角度进行编码，例如北风为0(度)、南风为180(度)天气属性按湿度大小编码，我们可以认为天气为“小雨”比“晴”湿度大，所以“晴”排在前面，“小雨”排在后面，但某天“阴”也不见得一定比某天“多云”湿度大，对于这种凭直观感觉难以区分的情况，任选一个排在前面即可;空气质量等级由好到差依次与 0、0.2、0.4、0.6、0.8、1 相对应.

2.2 输入属性筛选

本文使用典型的遗传算法对输入属性进行筛选.

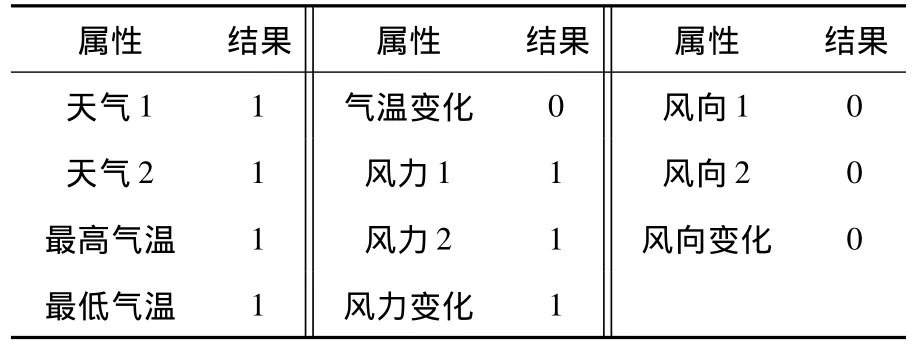
表1 输入属性筛选结果对应表

具体计算流程为:首先使用二进制编码方案对输入属性进行编码，若该属性参与运算则该属性的标志为1，若该属性不参与运算则该属性的标志为0.然后，使用预测值与实际值之差的绝对值的倒数作为适应度，对标志位串进行寻优.最后，得结果为11110111000，对应表如表1.

根据属性筛选结果及高度相关变量二选其一原则，最终选取天气1、天气2、最高气温、最低气温、风力1和风力2共6个变量作为输入.

2.3 数据关联方案

针对空气质量等级的预测使用了2类共10种输入输出数据关联方案，如图2.

图2 两类预测方案

类1为不需要天气预报的预测方案，方案1为当天的气象情况关联未来1天的空气质量等级，方案2为当天的气象情况关联未来1、2天的空气质量等级，……，方案6为当天的气象情况关联未来1～6天的空气质量等级.这类关联方案的理论依据就是样本输入对样本输出变化的影响，例如今天下雨会使明天的空气变好，但并不是所有的神经网络预测都可以使用该方案，因为使用该方案的前提是我们必须知道输入样本对输出的变化是有影响的.

类2为需要天气预报的预测方案，未来7天的气象情况可从国家气象局的预报获得，即认为未来7天的气象情况是已知的.方案7为未来1天的气象情况关联未来1天的空气质量等级，方案8为未来1天的气象情况关联未来2天的空气质量等级，方案9为未来1天的气象情况关联未来3天的空气质量等级，方案10为未来1天的气象情况关联未来4天的空气质量等级.

3 仿真预测

3.1 遗传算法优化方案

在本案例中，遗传算法对BP网络的网络结构、权值阀值的优化是分开进行的.

BP网络的网络结构包含网络层数和隐节点数两部分内容，网络层数通常为单隐含层结构，双隐含层结构较少，同时隐节点数通常为1～2个整数，例如，经典的鸢尾花数据集的最优隐节点数为8，即BP网络的网络层数、隐节点数是可以精确求得的.而BP网络的权值阀值一般为-3～3之间的浮点数，往往精确到小数点后数位，无论多少次运行遗传算法算法，每次的寻优结果还是会存在一定差异，即遗传算法搜寻到的最优权值阀值是存在误差的.假如把网络结构和权值阀值放在一起编码、优化，不仅增加了编码长度、寻优难度，使算法过早收敛的可能性变大，而且由于权值阀值的寻优结果存在误差，就会使原本可以精确求得的网络结构最优参数混入误差，所以两者不宜放在一起进行优化.

3.2 遗传算法优化网络结构

BP 网络的层数.Hecht-Nielson 已经证明［12］:具有偏差和至少一个S型隐层加上一个线性输出层的网络，能够逼近任何有理函数.实验证明［16］，多隐含层BP网络虽然可以略微提高预测精度，但学习训练时间会大大增加.综合考虑，本文选用了单隐含层结构.本文直接使用遗传算法对网络所需隐含层节点数进行了寻优，具体步骤如下.

采用二进制编码方案，使用测试数据集的预测值与实际值之差的绝对值的倒数作为适应度;使用遗传算法对隐节点数进行寻优，寻优范围为1～16(24)的整数，假如求得隐节点数超过14，则调整上限;设置初始种群为20，迭代次数为10次，运行算法.

在寻优过程中，初始种群数为20，隐节点数为1～16的整数，理论上，1次迭代就能完全覆盖寻优范围，而实际操作中，本算法的适应度计算结果是由BP网络预测值计算得来，而典型BP网络过早收敛的现象非常常见，所以算法仍需多次迭代才能达到理想效果.

对于训练集、测试集的划分以及重复验证问题，10次10折交叉验证是标准评估技术［22］，即把全部数据集据随机的分为10个部分，每部分数据的数量基本一致，其中1个部分做测试集，剩余的9部分做训练集，交替进行，直至每部分数据都做过测试集为止.然后重复进行10次取均值再取整即可.

3.3 遗传算法优化权值阀值

编码方案.遗传算法的编码方案有多种，其中以二进制编码方案和实数编码方案最为常见.权值阀值通常要精确到小数点后数位，实数编码方

其中:a'ij为变异后的个体;aij为变异前的个体;r为0～1之间的随机数;amax为个体上界;amin为个体下界;g为当前进化代数;Gmax为最大进化代数.

3.4 实验结果及分析

选取大连市2013年11月～2014年4月(共181个样本)的天气记录及空气质量等级作为训练数据，预测未来数天的空气质量等级.

为了验证算法的泛化能力，多次替换预测输入数据，运行算法，直至预测出2014年5～9月全部的空气质量等级，然后重复10次实验，统计预测正确率.预测正确率统计表，如表2所示.案特别适合于精度要求较高的遗传算法，所以选择了实数编码方案对初值进行了编码.

适应度函数.使用预测正确天数的个数作为适应度，即预测正确的个数越多该组权值阀值被选中的概率越高.

选择、交叉、变异.选择方案为最常用的轮盘赌选择方法;交叉方案选用算数交叉方案，这是由于算数交叉方案特别适用于实数编码;变异方案采用改进后的非一致变异方案，公式如下:

表2 预测正确率统计表

其中，采用数据关联方案8预测正确率最高，达67.1%.单次运行算法的预测误差图，如图3，规整后的分类效果图，如图4.

在表2中，方案1～6为不需要天气预报的预测方案，可以看出，预测正确率随着预测天数的增加而下降;方案7～10为需要天气预报的预测方案，可以看出，方案8的预测正确率高于其他方案，即当天的气象情况对第二天的空气质量影响较大.

图4 分类效果图

4 结论

影响空气质量等级的因素众多，例如，车辆、船舶的尾气、工业生产排放、居民生活取暖、垃圾焚烧、城市人口密度、发达程度、地形地貌、节日出行和气象条件等，都是影响空气质量的重要因素.本文仅以大连市2013年11月～2014年4月气象信息作为学习数据，采用多种方案，使用遗传BP网络对短期空气质量等级进行了预测，取得了较好的预测效果，对于污染防治、公众健康、出行日期选择都有一定借鉴作用.

［1］汪小寒，张燕平，赵姝，等.基于动态粒度小波神经网络的空气质量预测［J］.计算机工程与应用，2013，49(6):221-224.

［2］辛若波.基于遗传优化和贝叶斯正规化神经网络的空气质量预测研究［D］.济南:山东大学，2013:26-32.

［3］李国勇.智能预测控制及其MATLAB实现［M］.北京:电子工业出版社，2010:16.

［4］马丽慧，韩文喜，李阳.BP网络在高填方地基沉降预测中的应用［J］.土工基础，2013，27(1):14-16.

［5］沈清.神经网络应用技术［M］.长沙:国防科技大学出版社，1993:45-85.

［6］徐水春，张森文.遗传K均值方法在品种资源分类中的应用［J］.华南农业大学学报，2009，30(2):97-100.

［7］PIZZILEO B，LI KANG，MEMBER S.Improved Structure Optimization for Fuzzy-Neural Networks［J］.Fuzzy Systems，IEEE Transactions on，2012，20(6):1076-1089.

［8］邓凯，赵振勇.基于遗传BP网络的股市预测模型研究与仿真［J］.计算机仿真，2009，26(5):316-319.

［9］常辉.基于遗传BP网络的智能型电力负荷预测技术［J］.电脑知识与技术，2009，5(8):1962-1964.

［10］苏晨，李成义.基于遗传算法和BP神经网络的服装销售预测［J］.经营与管理，2012(2):110-111.

［11］韩亮华.遗传BP网络对临江河回水区叶绿素a的短期预测模拟［D］.重庆:重庆大学，2011.

［12］HECHT NIELSON R.Neurocomputing［M］.Boston:Addison Wesley，1990.