中国未来劳动力需求预测研究

王 颖，刘秋燕，杨芊羽

（北京师范大学 政府管理学院，北京 100875）

0 引言

近年来，一些机构和学者认为随着老龄化的加剧，中国经济发展的“人口红利期”将很快消失，劳动力优势也将消失。可见，中国未来的经济增长需要多少劳动力的支撑这一问题是判断劳动市场的重要指标，同时更是人口政策、社会保障、国家安全政策如何定位、如何调整的根本依据之一。

然而，对中国未来劳动力需求进行较为准确的判断却是一个难题。这首先是由于劳动力需求被较多因素影响。理论上，经济增长会引起对劳动力需求的增加，因此经济增长率和劳动力需求的增长率之间存在正相关关系。然而自上世纪90年代中期开始，中国就遭遇了“增长型失业”的困扰，作为人口大国，就业效应不足既浪费人力资源，也造成大量社会无业人口，从而威胁社会稳定。即使不考虑其他变量，仅仅预测未来经济发展速度以及劳动力需求弹性也很困难。已有的相关预测，在相同时期内的预测值却有很大差异，这主要是对未来就业弹性的估计不同造成的。

本文以德国的发展模式为借鉴，以我国产业就业结构为基础，推导出我国三大经济带三次产业的产值增长率、就业弹性这两个关键变量在未来的变化情况，从而最终预测我国未来（至2050年）的劳动年龄人口需求总量。

1 模型与数据

1.1 模型构建

就业弹性是在某一时期内就业数量的变化率与产值变化率之比。就业弹性系数越小，表示该产业对劳动力的吸纳能力弱；系数越大，表明该产业对劳动力的吸纳能力越强。针对就业弹性的测算方法主要是两种：一种是构建经济增长影响因素模型,利用对模型参数的估计测算；另一种是根据弹性的定义进行测算。

构建经济增长影响因素模型进行就业弹性估算，以新古典经济增长模型应用最为广泛，它的典型模式是：Y=AKαLβ，两边取对数变成：1nY=1nA+α1nK+β1nL+ε，估计参数值β,即得出就业弹性值，这种估计方法得不出具体某一年份的弹性值，模型中涵盖的影响经济增长的因素越多，那么模型参数就越多，则估计参数需要的样本点就越多，因此，上述模型的局限就在于只能对包含众多样本点的时间段进行估计。最终，本文将使用根据弹性定义方法测算就业弹性，这种方法对就业弹性的通常表达式为：

式（1）中ε表示就业弹性，L表示劳动年龄人口（就业）需求，Y表示GDP，ΔL表示劳动年龄人口的差值，ΔY表示GDP的差值，此模型反映了GDP每增长一个百分点对就业产生的影响。

由于无法得出时间序列中起始样本的就业弹性,并且通过发现两个变量间的关系是非线性的，因此本文设立模型：

对两个变量分别取对数，形成双对数线性模型：

式（3）中，L、Y分别表示劳动年龄人口（就业）需求和国民生产总值GDP，lnL表示劳动年龄人口的对数，lnY表示国民生产总值的对数，回归系数β1就表示就业弹性。本文在具体的分析中考察了模型的F值和拟合优度。

1.2 数据来源

本文的数据主要来源于历年《中国国家统计年鉴》，还有《德国统计年鉴》、《德国经济年报》，此外，还包括从国家统计局，国际货币基金组织（IMF）和世界经济合作组织（OECD）的相应统计信息网页中搜集的年度数据。

2 德国和中国产业就业结构变动规律

2.1 德国产业就业结构变动规律

德国就业结构、三次产业结构以及产值就业弹性的变化呈现出三大特点：

（1）从第一产业来看，上世纪50年代中期，农业的产值比重低于10%，此后下降速度更快，至今已跌至1%，就业份额也随着农业产值地位的下降迅速减少，第一产业的就业弹性几乎都是负值，农业产值的增加并没有带来就业的增长；（2）第二产业一直占据着重要的经济地位，产值比重接近50%，但是进入后工业化时期以来，制造业对总产值的贡献有所削弱，产值比重也由50%下降至30%。此外，第二产业就业比值的变动总体呈现出倒“U”型的变动规律。在就业弹性上，第二产业的就业弹性下降迅速且变为负值，其对就业的吸纳作用在逐步下降；（3）从第三产业来看，其产值比重、就业份额以及相应的就业弹性都呈上升态势。从上世纪80年代开始，第三产业的产值比重首次超越50%，2011年已经达到71.2%；就业份额也高居70.1%。

同时，德国产业结构发展表现出三大规律：首先，尽管工业化进程中不同阶段伴随着不同的主导产业，但是第二产业一直扮演着重要的角色。从19世纪中期至今，德国的第二产业一直在德国经济发展过程中贡献巨大。其次，在就业方面，德国初始以劳动密集型产业为主，逐步转向技术密集型。20世纪50年代，处于工业化中期的德国以劳动密集型产业为主导，对就业的吸纳作用增强，但随着工业化进程的加快，西德转向集成电路、机械、精细化工、家用电器、汽车等耗能耗材少，附加值高的技术密集型产业。到了20世纪90年代，德国产业结构调整的重心是加快以信息技术为核心的高新技术的发展，推进产业结构的高级化，高新技术的发展带动整个服务业的繁荣，第三产业的迅速发展对就业的拉动作用更加凸显（蒋智华，2005）。最后，产业结构的调整伴随着经济发展自然发生。德国1964年的人均GDP约为4513美元，且产值构成中，工业部门占据主导，高出服务业产值比重近10%，但是第三产业的就业吸纳能力要高于第二产业，这与我国的产业发展情况具有较高相似性。当前，我国正处于增长阶段转换背景下，从“工业经济”迈向“服务经济”的关键时期，具有明显的工业化中期特征，德国产业结构发展的经验值得借鉴。

2.2 我国东中西部地区产业—就业结构变动规律

为了探析我国产业就业结构的真实变动规律，进一步归纳得出我国东部、中部与西部的产业就业结构（见表1）。

我国东中西部产业就业结构变动存在较大的差异。一方面，虽然东中西部大体遵循“二、三、一”的产业分布，但是具体产值比重偏差很大。从第一产业来看，东部地区的产值结构相较中西部地区而言，下降较快且下降的幅度较大，从改革之初的26%降至6.9%，而西部地区的“第一产业”比重最大，大约为东部地区的2倍；三大区域第二产业的比重相差不大，但是在第三产业方面，东中西部的差别较大，东部地区分别比中部地区、西部地区高出“7.5%”、“6.2%”。

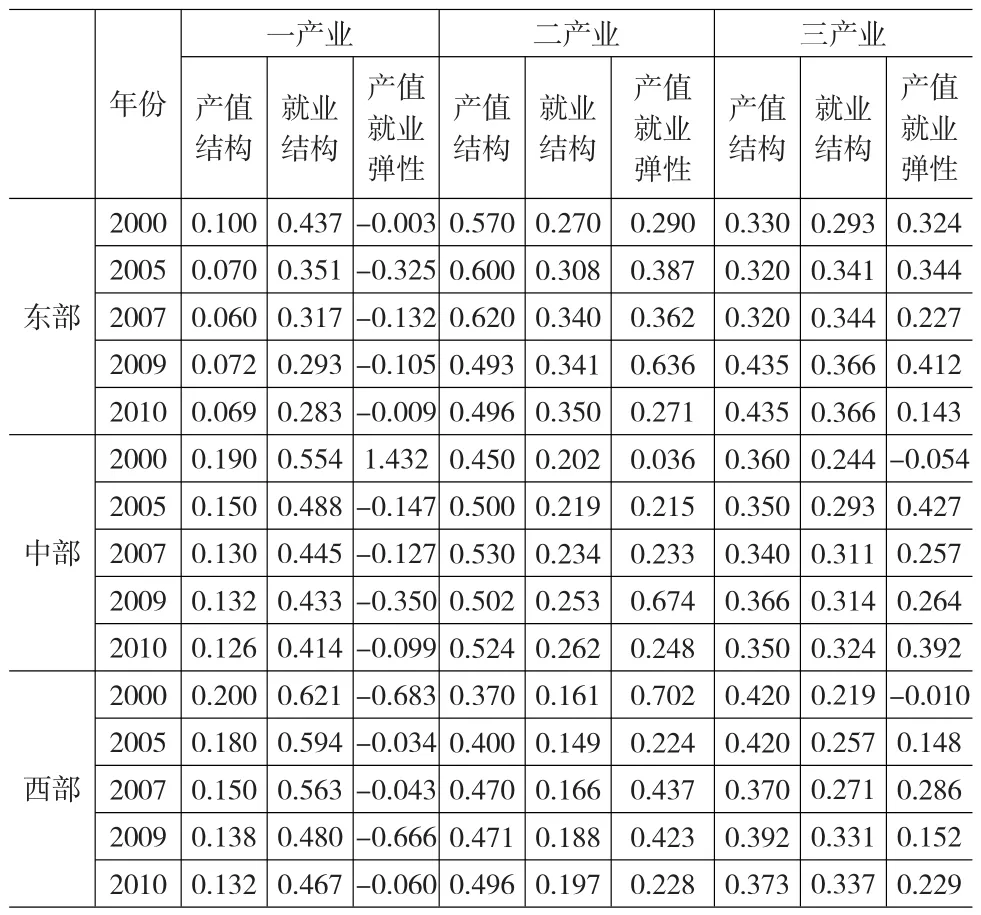
表1 我国三大地区的产业--就业结构

另一方面，从三个产业的就业结构来看，东中西这三大区域的差异比较明显。东部三次产业吸纳劳动力按照“三、二、一”的顺序分布，而中部和西部却呈现出“一、三、二”的分布规律。西部地区的第一产业就业比重约为东部地区的2倍，而其第二产业的就业比重不足东部地区的20%。就业结构与产业结构的协调性方面，“第一产业”的就业比重远高于其产值比重，其中2010年，中部地区第一产业的就业比重28.3%，远远高于其产值比重6.9%，而第二产业和第三产业的产值比重远高于相应的就业比重。从就业弹性上来看，东中西部第一产业的就业弹性均呈现下降趋势，第二产业与第三产业的就业弹性中西部地区与东部地区差别较大。近几年来中西部第二产业与第三产业的就业弹性有所上升，在一些年份中甚至超出东部地区，表现出较强的就业拉动潜力。

总体而言，我国东部地区非农产业就业比重显著高于中西部地区，上升幅度也比中西部地区要快，与德国总体的工业化趋势具有相似性。与此同时，东部地区表现出资本深化的发展特征，与德国工业化中期的产业结构特征一致。因此，可以将我国东部地区三次产业的劳动年龄人口需求预测参照德国的产业就业结构变动规律进行，在此基础上，中西部地区通过比照东部地区相应经济指标的发展趋势，以进一步拟合推测出其各自的劳动年龄人口需求。

3 中国未来劳动力需求预测

3.1 基于我国东、中、西部地区产业就业结构自身变动的规律预测

首先，根据我国东中西部三次产业的产值变化规律，将1978～2011年每十年划分为一个阶段，并求出各阶段三次产业产值增长率的平均值再将均值进行拟合，从而得到我国东中西部不同经济发展时期三次产业相应的产值增长率；其次，根据我国东部第一产业、第二产业和第三产业产值就业弹性系数进行拟合，得到各个产业的就业弹性系数均值，由此可拟合推得至2050年东部各个产业产值就业弹性系数模型；然后根据我国中部三次产业的就业弹性系数的发展规律拟合得到我国中部第一产业产值就业弹性系数均值为-0.246，第二产业产值就业弹性系数均值为0.213，第三产业产值就业弹性系数均值为0.254，可拟合推得至2050年中部三次产业产值就业弹性系数模型，并得到相应的就业弹性系数；最后，依据我国西部的三次产业的就业弹性系数发展规律拟合得到我国西部第一产业产值就业弹性系数均值为-0.141，第二产业产值就业弹性系数均值为0.244，第三产业产值就业弹性系数均值为0.234，可拟合推得至2050年中部三次产业产值就业弹性系数模型，并得到相应的就业弹性系数。

依据东中西部三次产业的产值增长率与就业弹性，可以推得我国东中西部不同经济发展时期三次产业的劳动年龄人口需求，并且通过我国东中西部地区三次产业的劳动年龄人口需求的变动趋势的预测，可以进一步加总推得我国未来总体的劳动年龄人口需求的变动趋势（见表2）。

3.2 基于我国东部地区参照德国的产业就业结构变动的规律预测

首先，推测我国东部地区在不同的经济发展期，它的三次产业产值增长率。利用德国第一产业产值增长率、第二产业产值增长率、第三产业产值增长率进行拟合，找到德国三次产业产值的变化规律，并依照我国东部地区三次产业的基础值得到我国东部地区三次产业的变化规律，进一步推算出东部相应年份的三次产业产值；其次，推测我国东部在不同经济发展时期的就业弹性，通过德国工业化进程中各产业各年产值就业弹性系数得到德国的就业弹性系数变化规律，并根据我国东部区域三次产业就业弹性的基础值得到我国东部地区三次产业就业弹性的变化规律，并进一步推算出东部各相应年份的三次产业的就业弹性系数。依据东部三次产业的产值增长率与就业弹性，则可以推得我国东部地区不同经济发展时期三次产业的劳动年龄人口需求。

在参照德国产业就业结构变动规律，预测我国东部地区三次产业劳动年龄人口需求的基础上，中西部地区通过比照东部地区相应经济指标均值的发展趋势，可以拟合推出其各自的劳动年龄人口需求。就中部地区而言，比照我国东部三次产业产值增长率与就业弹性的均值及其变动规律，可以发现其三次产业的产值增长率比东部地区各产业少1%，就业弹性系数则比东部各产业弹性系数变化趋势快0.01，可以拟合推得中部地区在不同经济发展时期的三次产业产值增长率与就业弹性；就西部地区而言，比照我国中部三次产业产值增长率与就业弹性的均值及其变动规律，可以发现西部三次产业产值增长率比中部地区各产业少1%，西部地区第一产业并比中部各产业弹性系数变化趋势快0.01，第二、三产业弹性系数变化趋势则和中部趋同，由此可以拟合推得西部地区在不同经济发展时期的三次产业就业弹性和产值增长率；根据西部三次产业的产值增长率与就业弹性，则可以推得我国西部地区不同经济发展时期三次产业的劳动年龄人口需求；最后，通过我国东中西部地区三次产业的劳动年龄人口需求的变动趋势的预测，可以加总推得我国未来总体的劳动年龄人口需求的变动趋势（见表2）。

4 结论

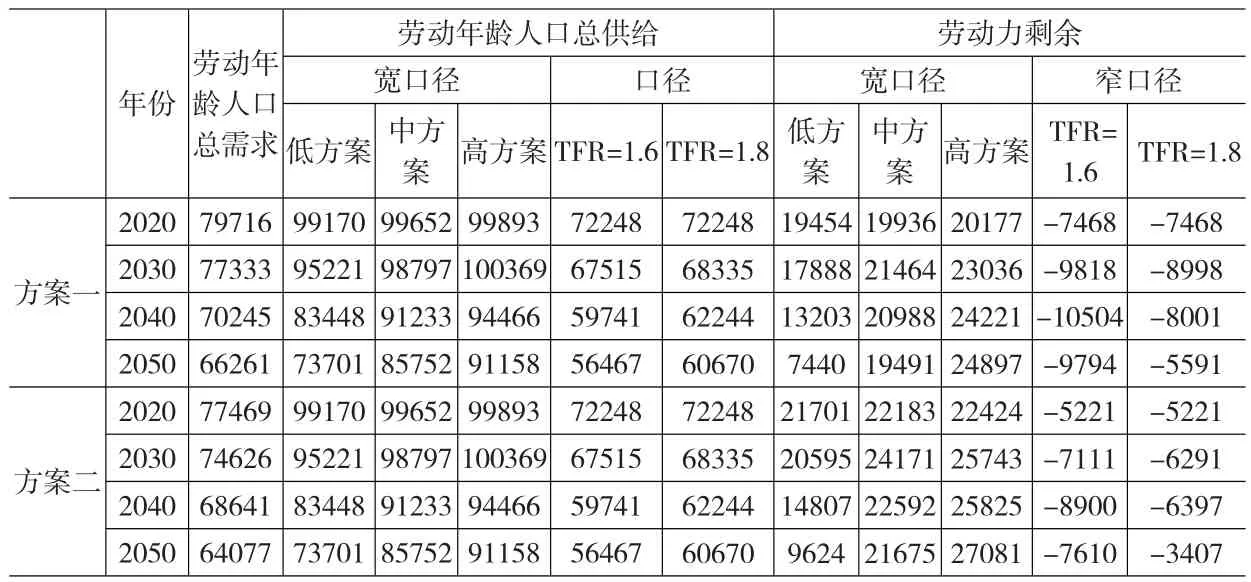
表3 我国未来的劳动年龄人口总需求（万人）

目前我国学者对未来劳动力供给状况依据不同的预测方案所得结果不尽相同，如《国家人口发展战略研究报告》（2007）、《中国人口老龄化战略研究》（2011）均指出中国是世界劳动年龄人口数量最多的国家，我国未来人力资源持续丰沛，劳动年龄人口2016年将达到10亿人左右的高峰，王金营等（2006）也作了大致的预测。彭秀建（2006）、王金营(2006)按照生育率较高方案得出的未来我国劳动力供给预测结果最高，并且两者较为接近；齐明珠（2010）的预测值最低。因此王金营(2006)、齐明珠（2010）的预测值可以作为宽口径和窄口径的代表，将其与本文得到的劳动力需求预测值做比较，可以对我国劳动力未来供求的态势做出全面、公允的判断。

方案一：基于我国东中西三大经济区域1978～2007年的产业就业结构变动规律预测我国未来劳动年龄人口总需求（见表3）；方案二：基于我国东部地区参照德国产业就业结构变动规律，中部和西部比照与东部的发展差距，预测我国未来劳动年龄人口总需求（见表3）。

比较方案一和方案二的预测结果，可以看出与宽口径的劳动力供给预测相比，在各个发展时期，劳动年龄人口剩余都在7440～19454万人之间，存在富裕的劳动力剩余，和窄口径劳动力人口供给比较，劳动力缺口在3407～10504万人之间，存在一定规模的劳动力短缺。

[1]齐明珠.我国2010～2050年劳动力供给与需求预测[J].人口研究,2010,(5).

[2]崔湘怡.我国经济增长中的产业结构优化和梯度转移[J].商业时代,2013,(18).

[3]贺长年.金融危机视角下的“德国模式”及其解读[J].商业时代,2011,(25).

[4]蒋智华，郑玉华.发达国家产业结构调整的特点及启示[J].经济问题探索，2005,(10).

[5]昝欣.我国产业转移的相关问题研究[J].发展，2012,（2).

[6]王金营，蔺丽莉.中国人口劳动参与率与未来劳动力供给分析[J].人口学刊,2006,(4).

[7]彭秀健，Dietrich Fausten.低生育率、人口老龄化与劳动力供给[J].中国劳动经学,2006,(04)．

[8]马忠东,吕智浩,叶孔嘉.劳动参与率与劳动力增长:1982～2050年[J].中国人口科学,2010,(1)．