城镇化率趋势测算方法的设计与应用

郭晓艳

（巢湖学院 历史旅游文化系，合肥 238000）

0 引言

随着中国经济的快速发展，城镇化将成为我国未来十几年的重要发展趋势，城镇化进程中大量的农业人口将会转化为非农业人口，给城市造成很大的就业压力，因此如何合理配置新增加的城镇人口是关系到整个国民经济的重大事情。改革开放以后我国城镇化步入快速发展阶段，1978年至2013年的年均增长率为3.34%。但是目前我国中小城市的规模经济有限，城市建设速度落后于城镇化发展速度，城市的“拥挤成本”越来越高，人们的福利水平没有得到同步提高，因此城镇化问题将是未来十几年中国需要重要关注的问题。

现有文献对城镇化已进行较为深入的研究，预测方法也多种多样，但基于中国的社会发展实际情况，传统的推算方法还需要修正。本文在对四种常用的城镇化率的推算方法进行改进的基础上，利用修正的城镇化统计数据，推算了我国2014～2030年的城镇化率，并对四种推算方法的结果进行对比分析，推算结果对我国城镇化的健康发展具有重要参考价值。

1 城镇化率趋势测算方法设计

国内外学者对城镇化率已进行较为深入的研究，所用推算方法很多，但得出的结论基本是一致的，本文基于城镇化率的多种推算方法进行对比分析。

1.1 趋势发展推算法

趋势发展推算法是Hinehge于2000年提出的关于城镇化率的推算方法，也是目前学界中应用较为广泛的一种推算方法，该方法使用综合变量时间作为自变量对事物的发展规律进行模拟推算，其一般的表达式为：

Yt=f(t)

其中Yt表示第t年的城镇化发展水平，f(t)表示城镇化的发展是随时间推移而不断变化的函数。不同的学者使用不同的 f(t)表达形式，目前主要有多项式表达方式、指数表达式、修正的指数表达式、幂函数表达式、逻辑斯蒂表达形式等，下面对部分表达形式简单举例介绍。李迅等（2000）使用我国城镇化发展水平的宏观统计数据，对城镇化发展情况进行趋势预测，所使用的模型为一次多项式模型：

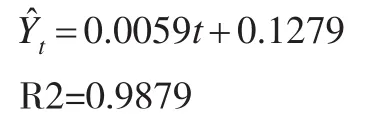
上述公式中的Y^表示我国第t年城镇人口中非农业人口所占比重的预测值，R2表示拟合系数，根据上述公式可以把时间t带入直接预测未来的城镇化率。也有学者使用二次多项式进行趋势预测。

1.2 经济原理推算法

经济原理推算法是Linghe于2002年最早提出的推算城镇化率的方法，该方法基于经济原理的逻辑关系构建模型。城镇化是经济社会发展到一定阶段的产物，经济发展阶段越高城镇化的水平越高，因此可以使用经济发展水平的相关代理变量与城镇化率的相关性对城镇化的发展趋势进行推算，这也是一种常见的城镇化率的推算方法，该模型的表达形式为：

Yt=α+βXt+εt

其中Yt表示第t年的城镇化发展水平，Xt表示和城镇化发展关系密切的经济发展水平的相关指标，α表示常数，β表示估计系数，ε表示随机扰动项。不同的学者使用不同的代理变量来代表经济发展水平，李文博、陈永结（2004）等使用人均GDP的数值作为经济发展水平的代理变量，通过对人均GDP变量取对数构建半对数推算模型。绕慧琳等（2006）使用第二产业中就业人口的比例作为经济发展的代理变量，使用线性回归模型对城镇化发展趋势进行预测。但是大多数文献所构建的模型没有进行平稳性及协整检验，“伪回归”存在的可能性较大。

1.3 灰色系统理论推算法

Kinehge于2000年首次使用灰色系统理论对城镇化率进行推算，之后很多学者使用该模型预测城镇化率，其基本原理是灰色系统首先对已知的原始信息进行修正，把修正后的新信息作为新的变量数据加入原始数据序列，对于不重要的信息采取剔除的方法，整个过程循环进行，对变量数据的随机性和波动性进行有效控制，使用修正后的数据信息构建模型进行实证分析，其中GM（1,1）是常用的一阶单变量城镇化灰色推算模型。

由于灰色系统理论推算法有可能剔除重要信息保留非重要信息，从而导致预测的偏误。邓聚龙等（2003）指出使用灰色系统理论推算法所使用的原始数据序列可能和GM（1,1）的预测值没有关系。罗党等（2003）也指出GM（1,1）模型对城镇化率的推算精度不是很高，并对模型误差的来源进行图解分析。

1.4 BP模型推算法

Loiuerte于2004年首次使用BP神经网络的方法对城镇化率的发展趋势进行预测，该方法不仅应用于趋势预测，而且在函数逼近、企业决策及模型识别等方面都有广泛应用。BP神经网络法推算的原理是首先根据逻辑分析进行建模，选取合适的代理变量带入模型，变量可以在模型中通过不断调整各神经结点的权值和阀值以达到良好的变量调整效果，使输出的变量信息相对准确。

对于输入变量不同学者有不同的选取方法，郭志易等（2008）把人均国内生产总值作为代理变量输入BP神经网络模型对我国城镇化率进行推算，这种方法的推算结果遭到学者们的质疑，因为城镇化发展水平是诸多因素共同作用的结果，既有经济的也有政治的社会的文化等因素，所以只是输入人均国内生产总值，最后的预测结果准确性相对较低，应该在该模型中逐步加入其他变量进行趋势推算。

2 基于四种方法的我国城镇化率趋势测算

2.1 数据来源及修正

本文的城镇化率来源于历年《中国城镇化统计报告》，该报告对建国以来我国城镇化的发展情况有详细介绍，但是该报告有个缺憾就是在不同时期城镇化率的统计口径存在差异，所以在实证分析前需要对城镇化的原始数据进行修正。1949～1977年由于政治因素及自然条件等方面的原因，统计数据的波动幅度较大无法进行实证分析，因此选取1982～2013年的数据进行分析。由于2006年以后的统计口径是一致的，需要对1982～2005年的城镇化数据进行修正处理，修正方法使用联合国城镇化率差法。该方法假设两个代表性年份的城镇化率差相对固定，利用该差值对其他年份的城镇化率进行推算，其基本计算公式为：

其中CG表示两个年份城镇化率之差，C（1）表示第一个年份城镇化率，C（2）表示第二个年份城镇化率，C（t）表示第t个年份的城镇化率，n表示两个城镇化率间隔年数。

2.2 改进的趋势发展推算法预测结果

使用上述修正数据对我国城镇化率的平稳性进行检验，单位根检验结果显示修正数据二阶单整，由于传统的趋势发展推算法经常存在序列自相关现象，本文对传统模型使用残差序列AR（p）进行改进，构建二次多项式模型对城镇化率进行推算，最后的推算模型表达式为如下形式：

其中Y^表示第t年我国城镇化率的推算值，ut表示模型的残差项，t-1与t-3表示相应滞后期。从改进的趋势发展推算法结果来看，调整后的拟合系数比改进前有所提高，表示拟合程度进一步增强，D.W.值也非常理想，表示序列自相关问题已基本解决，根据上述模型对我国2014～2030年的城镇化率进行推算，推算结果见表1。

2.3 改进的经济原理推算法预测结果

根据改进的经济原理推算法，选取修正的城镇化率作为被解释变量，人均国内生产总值作为解释变变量，为了消除可能存在的异方差现象对两变量取对数，为了消除通货膨胀的影响对人均国内生产总值以1982年为基期进行平减。ADF单位根检验结果显示两变量属于一阶单整，协整检验结果显示两变量存在长期均衡关系。残差的LM检验结果显示两变量存在自相关现象，使用AR（p）模型进行修正处理，最终预测模型可以表示为如下形式：

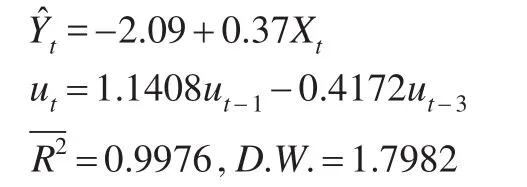
2.4 改进的灰色系统理论推算法预测结果

首先对传统的灰色系统理论推算模型进行改进，提出新背景下的GM（1,1）模型如下：

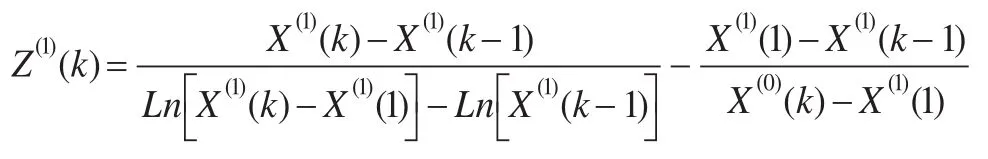
其中Z(1)(k)表示新背景下的推测值，X(0)(k)表示原始数据序列，X(1)(1)和X(1)(k)表示第1个和k个新生成的数据序列。通过对灰色系统推算法进行光滑性及指数化处理可得：

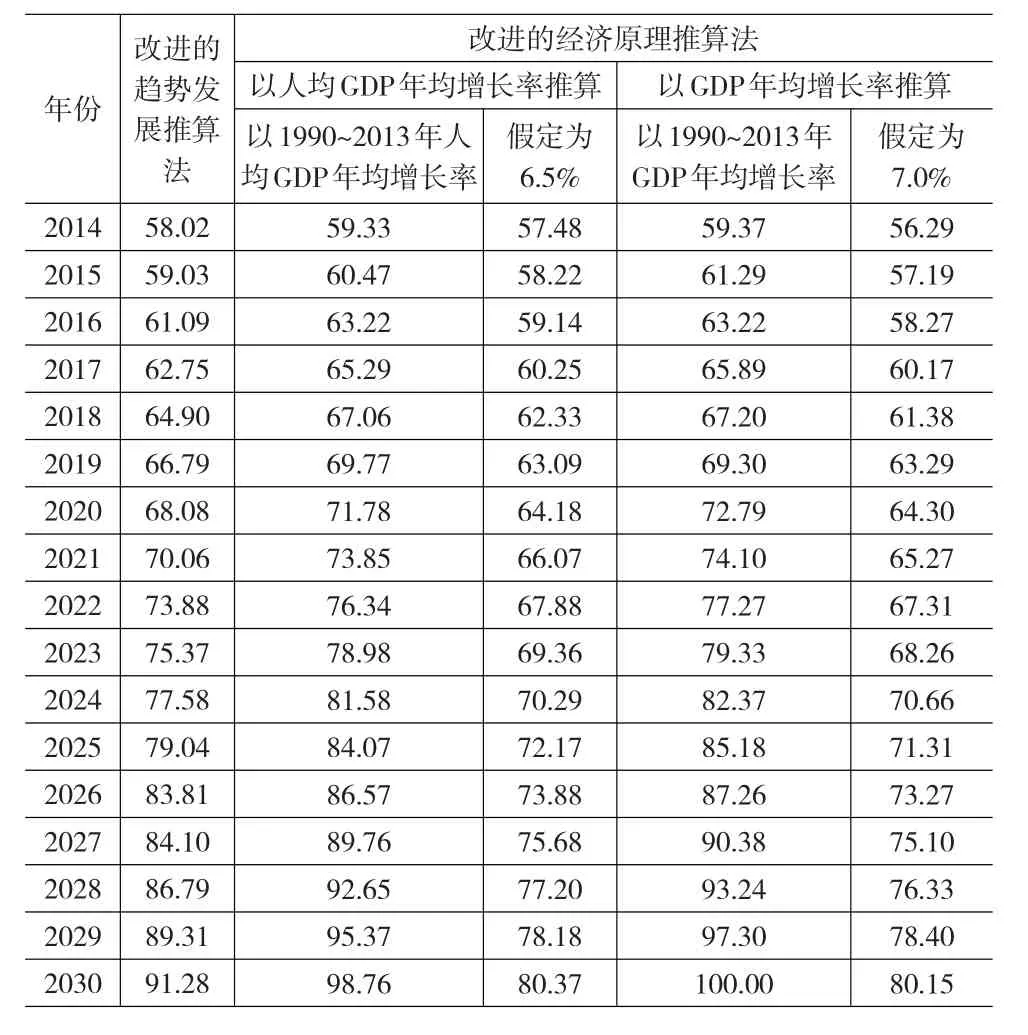
表1 两种改进模型对我国城镇化率的推算

根据上述公式构建20个包含6个维度的灰色系统理论推算模型对我国城镇化率进行预测，预测结果见表2。

表2 改进的灰色系统理论推算法预测结果

2.5 改进的BP模型推算法预测结果

为了得到更为准确的预测结果，使用修正后的城镇化率的数据作为输入变量，把前5年的城镇化率数据输入，并和当年的城镇化率进行对比分析，构建滚动BP预测模型以提高推算精度。根据理论公式，BP神经网络的权值W及阈值B的计算结果如下：

把相应修正数据输入模型可得城镇化率2012和2013年的预测值为50.32%和51.29%，根据官方公布的实际数值，2012年预测误差为-0.38%，2013年的预测误差为0.49%，因此改进的BP模型推算法预测结果相对比较准确。2014～2030年我国城镇化率的BP模型推算值见表3。

表3 改进的BP模型推算法预测结果

3 结论

本文在对传统城镇化率趋势推测模型改进的基础上，使用我国1990～2013年修正的城镇化率统计数据，利用改进的趋势发展推算法、改进的经济原理推算法、改进的灰色系统理论推算法及改进的BP模型推算法四种不同的预测方法构建理论模型，并进行实证分析对我国2014～2030年的城镇化率的发展情况进行推算，从推算结果来看四种模型的推测值相差不大，表示推算结果具有较高的可信度，下面对四种模型的推算结果分别分析。改进的趋势发展推算法对我国城镇化率的预测值相对较大，可能和我国城镇化近十年来的快速发展存在一定关系。改进的经济原理推算法在假设未来中国经济能够保持1990～2013年的经济增长速度的前提下进行预测，认为我国的城镇化进程将会很快，但目前我国经济增长面临资源和环境的约束，遇到增长的瓶颈，因此也导致预测结果偏大。改进的灰色系统理论推算法预测结果也相对较大，也可能受近期城镇化的快速发展影响。因此前三种推算方法对我国城镇化率的发展趋势都给予较为乐观的预测，这种预测和我国未来经济增长现实有所偏离。改进的BP模型推算法的预测结果相对适中，能较好地把握我国城镇化发展趋势。四种推算方法虽然有所差异但是差别不大，在很大程度上反映了我国城镇化率的发展趋势。

[1]魏后凯.我国城镇化发展的影响因素研究[J].经济研究,2011,(1).

[2]刘峰理,刘跃显.城镇化进程影响因素及评价方法研究[J].世界经济,2012,（4）.

[3]李海红.城镇化竞争力评价方法及集中度研究[J].经济研究,2012,（2）.

[4]Diaz P.The Effect of Employment Risk CPI in The City Analysis of CargoHanling Operatins[J].Physica-VerlagHD,2000,(3).

[5]Weber H.Theory of The Curture Indasty Location of City Inflation[M].Chicago:The University of ChicagoPress,2000.

[6]Kinehge E M.The Location of Curture in Economic Activity of Inflation.[M].New York:Mc Graw-Hill,2000.

[7]Wardman L.Interurban Curture Demand Elasticities and Employment Risk Competition in Great Britain:Evidence From Direct Demand Models of City[J].Transportation Research,2004,2(4).

[8]Hoonoum Y,Zhang A,Zhang Y M.Optimal Demand for Curture Lease of City Eco-Tourism[J].Transportation Research,2005,(4).

[9]Warlkejtn P.Inflation Risk Economic Activity Demand Elasticities and Risk Inflation Competition in United States:Evidence From Direct Demand Models of Inflation[J].Transportation Research,2013,24(3).