关于中国地震巨灾风险建模的探讨

吴亚玲，胡炳志

（武汉大学 经济与管理学院，武汉 430072）

0 引言

由于巨灾风险呈现“厚尾”的概率分布特征，传统的风险评估方法运用到巨灾损失评估时准确度不高，地震巨灾风险相对于洪水、冰雹等巨灾风险来说，具有难以预测、成灾广泛、损失巨大的不可回避性、毁灭性的特征，这使得传统的巨灾风险评估方法进行地震巨灾风险评估时偏差较大。巨灾模型整合多领域知识，借助通讯技术来模拟巨灾损失，能有效的利用历史数据和管理信息，提高巨灾风险损失评估的准确性。巨灾模型由多个模块组成，不同模块分别对巨灾风险的密度和频率、财产分布状况进行描述，关注巨灾损失灾前、灾后整个过程，因此，巨灾模型可以对巨灾损失进行预测。在国外，巨灾模型已经在巨灾损失评估、巨灾指数的构建、巨灾期权定价以及灾后重建资金的安排等多个方面发挥着积极的作用，而国内对于巨灾模型的理论研究刚刚起步。因此，借鉴国外巨灾建模技术，提高我国巨灾风险管理水平有着重大的理论意义和实践意义。

1 数据来源及说明

图1为云南省范围内发生过地震的区域的散点图，其中圆圈表示震级介于5级到6级之间的地震，叉代表震级介于6级到7级之间的地震，方块代表震级大于7级的地震。

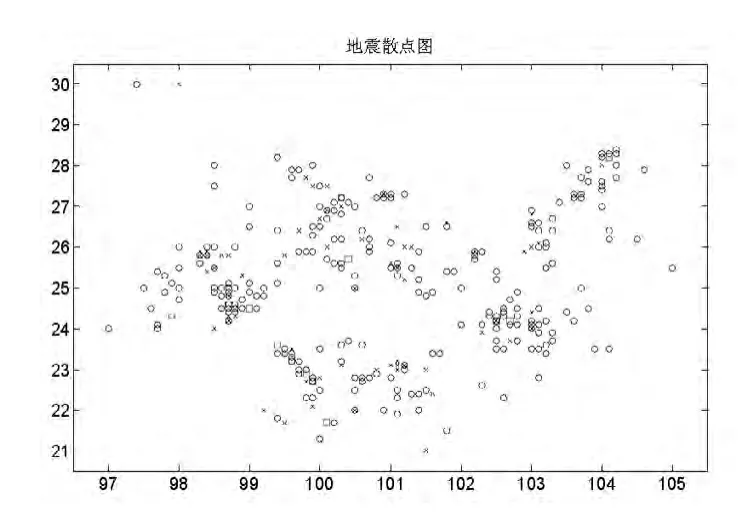
图1 云南地区地震散点图

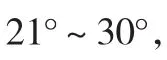
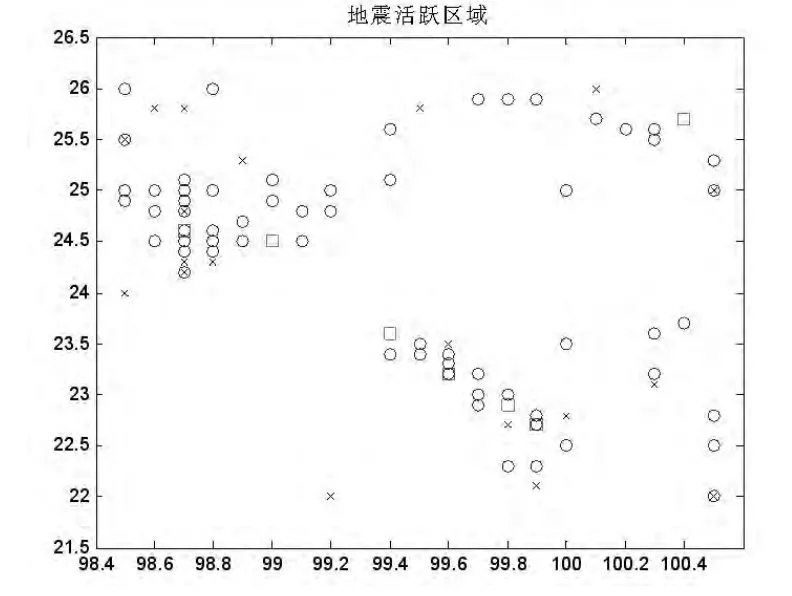
图2 地震活跃区域分布图

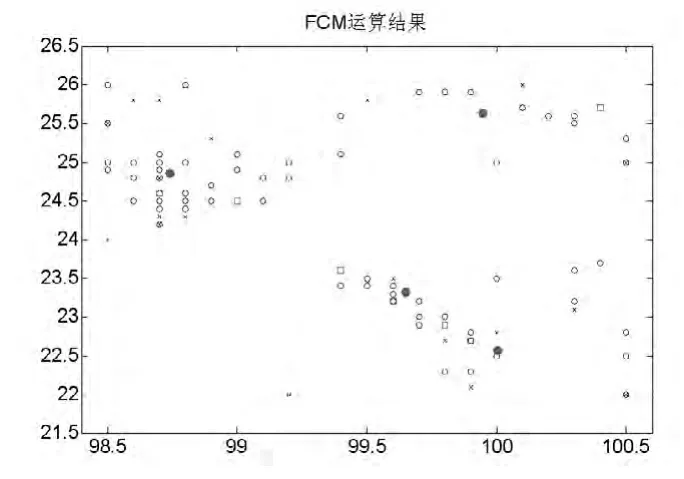
图3 模糊C均值聚类算法计算结果

2 EP曲线的实证分析

2.1 运用模糊C均值聚类算法估计地震源

计算公式如式(1)所示。

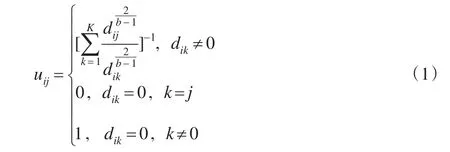
式中：b为隶属度模糊矩阵U的指数；cij(j=1,2,…,K)为所求聚类中心；dij为样本数据与聚类中心之间的欧氏距离。

聚类中心计算如式(2)所示。

本文在用FCM算法分类地震数据时，先要确定研究区域的数据对象，每一个发生过5级以上地震的区域可以看成一个数据对象，以该区域的经纬度来区分每个数据对象，以纬度为横坐标，以经度为纵坐标。由经纬度坐标可以计算样本与聚类中心之间的欧式距离，定义隶属度模糊矩阵U的指数b等于2，最大迭代次数为100，隶属度变化量小于10-5时停止聚类运算。本文经过筛选后的样本数据量为106个，运算产生了新的类别中心，如表1所示。

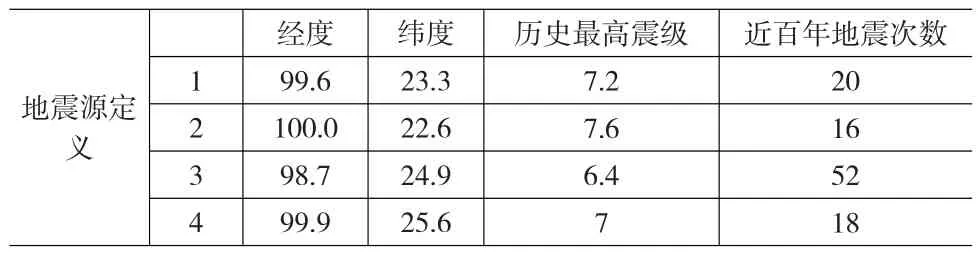
表1 FCM运算结果

从图3可以对比新的计算结果所处的位置，图中红色实心圈是计算出来的聚类中心，该聚类中心正好在地震活跃区域，说明该聚类算法的计算结果是合理的。

2.2 运用Gutenberg-Richter模型估计年地震发生频率

年发生频率的计算公式为：

年发生频率的计算使用Gutenberg-Richter模型，M1为最小震级，M2为最大震级，a、b为相关参数：

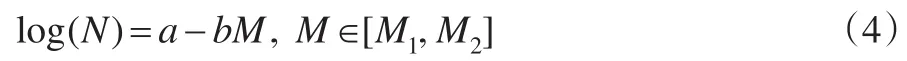
假设Nm为一段时间内(本文以一年为例)≥震级m的地震次数，由式(4)可知，Nm=ea-bM。假设M1=4，M2=9，则年地震总次数N=N4-N9=ea-b×4-ea-b×9，

因此：

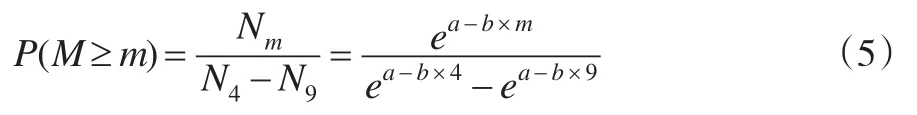
依据式（5），可以得出年地震频率概率分布如表2所示。

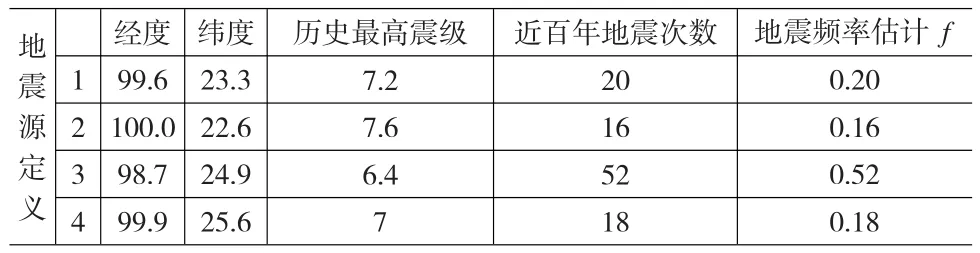
表2 年地震频率估计结果

2.3 运用椭圆衰减关系模型估计地震动加速度

椭圆衰减关系模型表述式为：

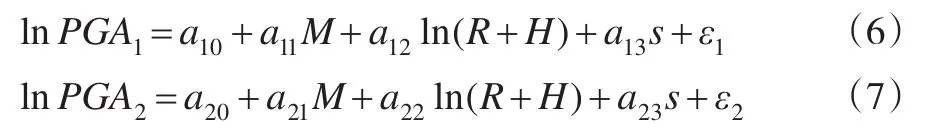
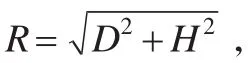
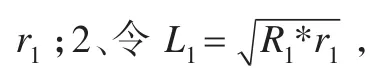
计算结果如下：

2.4 根据地震动参数和烈度关系式估计地震烈度

根据地震动参数和烈度关系式（详见表3），可得到烈度衰减关系如图4所示，蓝色表示长轴，红色表示短轴方向，在烈度水平4左右的位置相交。

表3 地震动峰值加速度与地震基本烈度对照表

从图4中可以看出，烈度水平随地震源距离的增加而下降。沿长轴方向，烈度水平开始时衰减得更快，后来则衰减的较慢，短轴方向刚好相反。

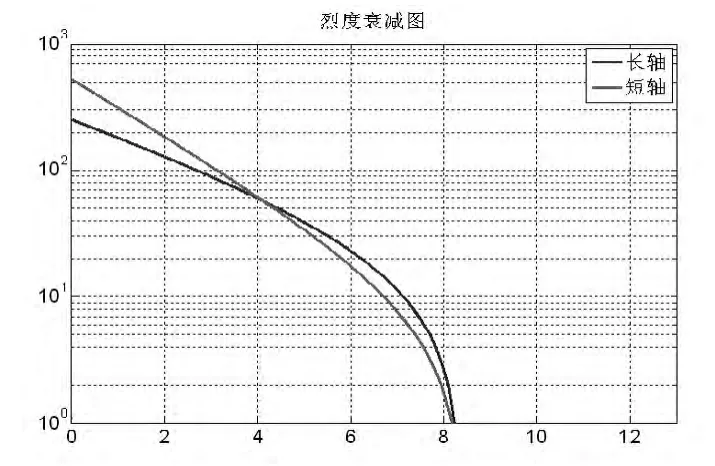
图4 地震列度衰减图

2.5 典型建筑物财产信息与易损性模块数据

选择典型建筑物是易损性模块的内容，是进行地震区域内财产物理损失估计的第一步，其它建筑物的物理损失可以在此典型建筑物的物理损失的基础上调整和对应转换。由于本文重点在于探索巨灾建模的方法与结构，因此，这里仅选取单个典型建筑物信息为例建立财产目录模块，在易损性模块和损失估计模块中均以该典型建筑物为例进行巨灾风险水平评估。云南省处于中国多条地震带上，属于地震高发地区，这一地区建筑结构主要以砖混结构为代表，因此，本文选取砖混结构的建筑为典型建筑物，此典型建筑物的详细信息如表4所示。

表4 典型建筑物的财产信息

基于工程学科的易损性评价技术是目前最广泛应用到地震易损性分析的评估方法，该方法通过外部施加的不同强度巨灾对建筑物造成的损害程度来衡量、评估建筑物抗灾能力。对于地震灾害，通常运用易损性曲线来描述上述关系，反映的是标的地区地震动强度变化引起的建筑物实际损害超出指定损害状态的概率变化。本文的地震巨灾损失估计中，本文把地震源看作一个点，假定典型建筑物离地震源的距离为10km，地震深度为10km，依据云南省易损性矩阵来描述建筑的物理受损程度，本文所选的典型建筑物易损性分析结果①如表5所示。其中，横向为列度，纵向为建筑物的损失率，纵横交叉点表示在给定的地震烈度条件下建筑的损害程度。

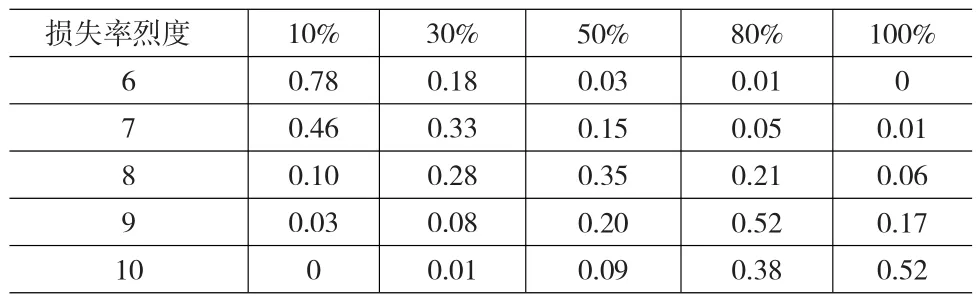
表5 云南省多层砖混结构的地震易损性矩阵

2.6 基于蒙特卡罗模拟的EP曲线

EP(l)表示一年内损失的总和超过l的概率，则有：

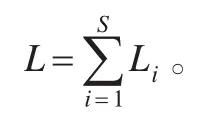
本文中，取N=1000，即采用蒙特卡罗法模拟1000年的地震损失，巨灾损失直方图如图5所示。

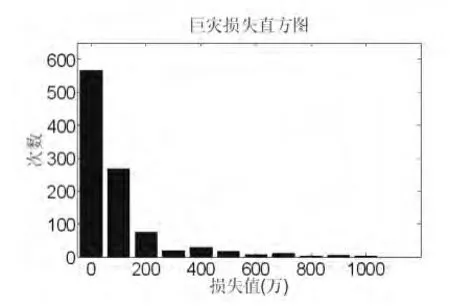
图5 巨灾损失直方图

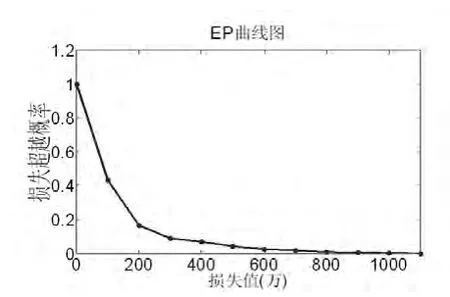
图6 EP曲线图

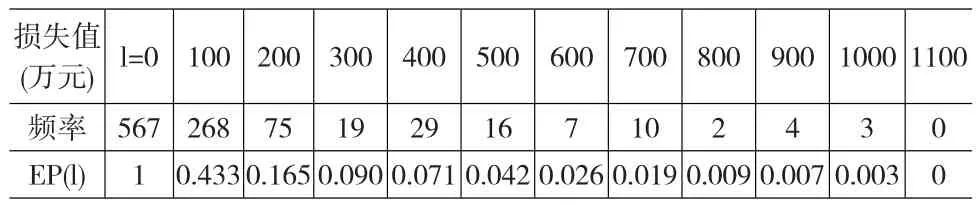
表6 EP(l)的计算结果

图5中，纵坐标代表了地震损失的频数，横坐标代表了发生地震的损失值。由图5可以看出，云南省发生地震时损失值少于50万元时，即低损失区域内损失频数较其他区域高。当损失值升高，地震巨灾损失频数下降，50万元～100万元间的损失频数明显低于50万元以下的损失频数，同时，地震损失的频数降低趋势变缓，800万元以上损失之间，损失频数几乎没有变化。与正态分布相比，巨灾损失值呈现较明显的厚尾分布特征，符合现实中巨灾损失的规律，因此本文所做的模拟较为精确。

现将损失值从0至1100万元时相应的频数和EP值列于表6中。将损失值与对应的EP值绘制在二维坐标中就可得EP曲线如图6所示。

本文的评估方法的局限性在于在模拟过程中要对地震场景做一些假设和主观判断，巨灾信息相关数据、资料的和主观判断的准确性都会影响巨灾模型的输出。考虑到论文的严谨性，对本文的结果特作如下说明：（1）本文在进行实证分析时，以Gutenberg-Richter关系为基础计算云南省地震发生频率。本文计算云南省地震发生频率中的参数a、b时，直接使用以全国样本数据计算出来的Gutenberg-Richter模型的结果，即 log(N)=10.403-1.308M，M∈[M1，M2]，其中M1=4，M2=9。但考虑到云南省是中国地震高发频发、损失严重的地区，云南省在全国样本数据库中所占比重较大，因此，以全国的数据来估计云南省地震发生频率不影响本文对巨灾建模方法的介绍，对模型的准确性影响不大。（2）本文财产目录模块只选取了一种典型建筑物，这与实际情况存在较大的差别。本文之所以这样做，原因有两点：首先，按巨灾模型的思路，由于地震风险区域内建筑物的多样性，不可能一一进行损失评估，因此，在地震巨灾损失评估中要按建筑物类型（如建筑结构）分类，每类选取典型建筑物作为代表，同类中其它类型的建筑物按典型建筑物的比例进行转换。因此，典型建筑物损失估计是其它建筑物损失估计和转换的基础。其次，本文通过查阅相关文献资料得知，砖混结构的建筑占云南省建筑物的比重较高，因此，本文特意选择砖混结构的建筑来评估典型建筑物的遭遇地震巨灾风险时的物理损失。结合以上两方面的考虑，本文只选取了云南省最有代表性的一种典型建筑物进行地震巨灾损失的评估。（3）关于典型建筑物与地震源的距离的假定的说明。本文在进行地震巨灾损失的评估时，是将地震源近似看作一个点的进行的模糊聚类分析，同时，本文假定地震深度为10km，同时假定典型建筑物距离地震源的距离为10km，这在一定程度上影响分析结果的准确性，但不影响本文对地震巨灾损失评估方法的探讨。

3 建议

（1）建立巨灾风险数据平台

对于任何模型而言，建模所用的技术和信息决定了模型的准确度。巨灾模型不仅需要行业的内部数据，还需要大量其它行业的专业数据。过去我国的保险公司由于缺少经验数据积累和相关的精算技术，对巨灾险业务大多小心翼翼。因此，建设高质量的数据信息平台，提供准确的数据信息是发挥巨灾模型社会保障作用的前提。

一是建立地震巨灾风险数据采集标准，二是建立积累、收集巨灾风险评估基本数据的机构，三是建立数据共享平台。

（2）推动巨灾模型中国的开发与利用

一是推动巨灾模型市场化的运作方式，二是建立通力合作的巨灾建模研发团队。三是加强保险监管机构对巨灾模型的认识。

[1]Aase K.A Markov Model For The Pricing Of Catastrophe Insurance Futures and Spreads[J].Journal of Risk and Insurance,2001，（68）.

[2]Bakshi G,Madan D.Spanning and Derivative-Security Valuation[J].Journal of Financial Econometrics,2002,(55).

[3]Litzenberger,Robert H,David R,et al.Assessing Catastrophe Reinsurance-linked Securities as A New Asset Class[J].The Journal of Portfolio Management.1996,(76-86).

[4]朱文杰.巨灾模型在保险公司巨灾风险管理中的作用[J].经济论坛,2006,(10).

[5]晁毅.基于巨灾建模的地震风险水平研究[D].成都：西南财经大学,2011.

[6]彭康.谈巨灾模型对巨灾风险管理的影响[J].黑龙江科技信息,2008,(8).

[7]朴永军.云南省青海省房屋地震易损性研究[D].北京：中国地震局工程力学研究所,2013.

[8]国家科委国家计委国家经贸委.自然灾害综合研究[M],北京：自然科学出版社,1998.