库存空间约束下多药品最优订购策略研究

周 颖，罗 利，吴晓东

（1.四川大学a.商学院；b.华西附属医院，成都 610064；2.四川大学 锦城学院，成都 611731）

0 引言

医院药品库存管理是医院管理中的重要环节，在我国，药品存货占医院流动资金的比例普遍达到了40%～60%，而许多其他行业的存货占流动资金的比率低于30%[1]。长期以来，大型公立医院药品订购量仅由采购人员凭经验确定，并不考虑库存成本，库存容量和变质损耗等情况。如果医院药品订购量过多，库存量过大，不仅积压资金，影响医院资金周转，而且还会占用库存空间导致药房空间不够用。如果订购量太少则发生缺药现象，不能满足临床用药，影响医院的服务质量[2]。因此确定合理的药品的订购量，成为了医院药品管理中亟待解决的问题。

四川大学华西医院是当今全世界单点规模最大的医院，是我国西部疑难危急重症的国家级诊疗中心。目前，华西医院三座住院大楼的配药和送药均由中心药房完成。每天早上，中心药房根据前一天的固定医嘱把患者需要用的药品配好，以护理单元为单位由中央运输科的人员配送到各个科室处。至于中心药房的药品采购则是每周通过医院信息系统自动做出药品采购计划。各种药品的具体采购数量则是参照一周的用药量来确定。由于医院各种药品的需求可能并非是平稳的，可见其现有的以“一周的用药量”作为采购量的做法是不合理的，产生严重的药品积压，导致中心药房的储存空间不足，并且也会影响到各科室用药的准确性。因此，本文选择存在问题较为突出的中心药房进行研究。

本文根据华西医院住院药房的实际情况，在允许缺货和存在订货提前期的前提下，以库存空间为约束条件，建立了以库存总利润最大为目标的数学模型，并给出了基于简约梯度法的算法，最后利用matlab软件进行了数值仿真。

1 本文的假设和符号说明

本文中的数学模型基于如下假设：

（1）各种药品之间需求率互不影响，且服从指数分布；

（2）各种药品的变质率互不影响，为常数；

（3）存在订货提前期，且提前期为常数；

（4）在计划时段初,各种药品库存量为0。

本文中的符号说明：

各种药品的需求函数为D(t)，在(0，T]内D(t)随时间呈指数变化，即 D(t)=λieβtt，其中 λi＞0，0＜βi＜1；

θi(t)为各种药品的变质率，为常数且0＜θi(t)＜1；

Ii(t)为t时刻产品i的库存水平；

tp为货物的提前期，即补货时间，为常数；

qi(i=1，2，…，n)为各种药品的订购量；

C0i为各药品的的订购成本（只与各药品的订购次数有关，而与各药品的订购数量无关）；

Hi为各药品的单位库存成本；

C1i为各种药品的单位购买成本；

Ti为各种药品的库存订购周期，且当t=Ti时，Ii(t)=0

DCi为药品i的变质数量；

TRi为药品i的销售收入；

pi是销售单位药品i的价格；

Hi是单位药品i在的库存成本；

Si是单位药品i在的缺货量；

wi是分配给单位药品i的空间；

W是总的库存空间；

πi(qi)是药品i在一个周期内运作的总利润；

π是系统一个周期内运作的总利润；

Tei为药品i的保质期；

ai医院中心药房的服务水平；

δi医院中心药房的最低服务水平；

μi订货周期内的需求量。

2 模型的建立

2.1 模型描述

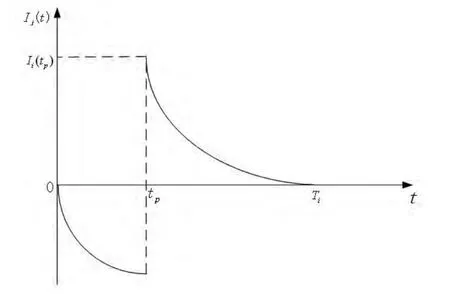
图1 某种药品库存水平变化图

根据模型描述，建立微分方程如下：

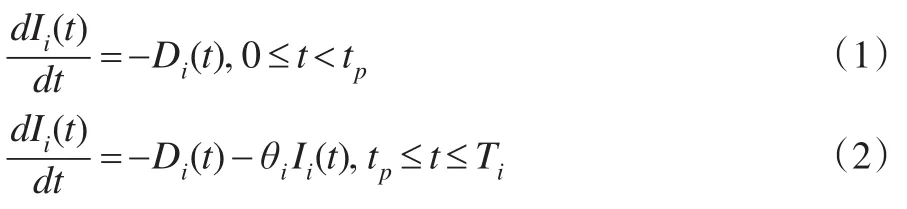
其中：方程（1）描述了当产品i在订货提前期时，造成产品i库存水平不断下降的原因是顾客需求的到来，此时药品i库存水平≤0，即缺货；方程（2）描述的是当产品i在订货提前期之后且在库存水平下降到0之前，造成库存下降的原因是顾客需求的到来及自身库存产品的变质。

将 D(t)=λieβtt，当 t=Ti时，Ii(t)=0 带入（1）（2）可得到药i在t时刻的库存水平方程：

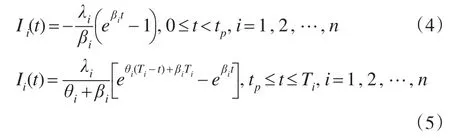
将t=tp代入（4）式可得药品i在[0，tp)时间内的缺货量；将t=tp代入（5）式可得药品i在t=tp时刻的库存水平。那么，产品i的订购量qi应为药品i在[0，tp)时间内的缺货量与在t=tp时刻库存水平之和：

问题（P1）解决的目标（15）是寻求每种药品的最优订购量q1，q2，…，qn的值，使其在单位时间内总的利润最大，（16）保证分配给所有药品的空间不大于仓库总的空间，（17）保证了中心药房的服务质量以及分配给每种药品空间应在一个范围之内，即有一个最大值和最小值，且最小值一定大于0。

3 模型求解-简约梯度法

问题（P1）是带有线性约束的非线性规划问题，又有定理2知，它是关于 q1，q2，…，qn的凸规划，因此，采用简约梯度法一定可以求得最优解。简约梯度法[4]的基本思想是把变量区分为基变量和非基变量，它们之间的关系由约束条件确定，将基变量由非基变量表示，并从目标函数中消去基变量，得到以非基变量为自变量的简化的目标函数，进而利用此函数的负梯度构造下降可行方向。

（4）求最大有效步长 λmax，从 q′(k)出发，沿 dk搜索：

minf(q′(k)+ λd(k))

s.t.0≤λ≤λmax

得到最优解λk；

（5）令 q′(k+1)=q′(k)+λkd(k)，置 k:=k+1，转步骤（2）。

4 数值算例

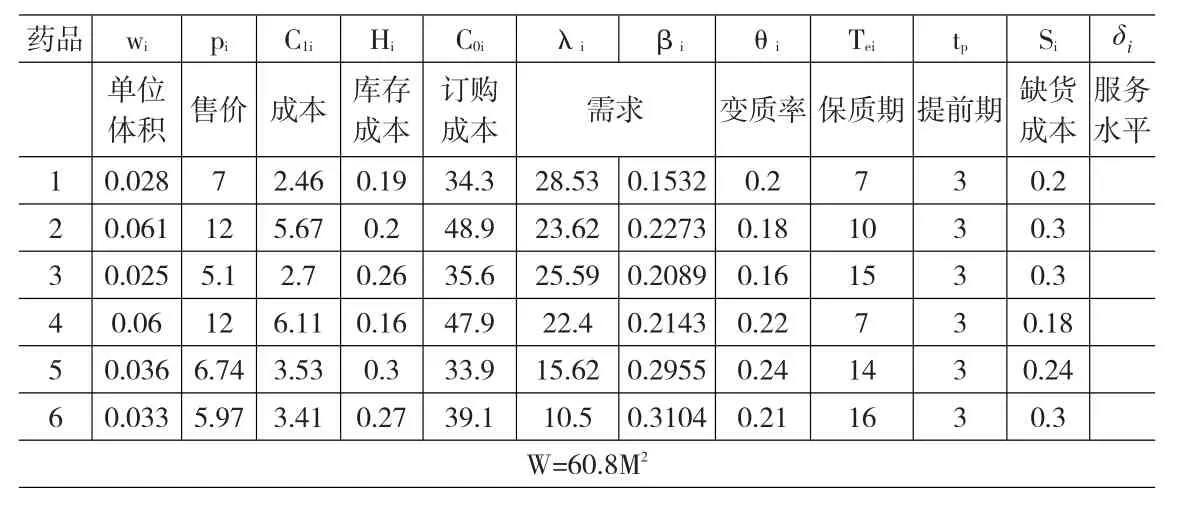
表1 各参数取值

为了更好的验证本模型，论文选择6种药品为例数值计算。其中参数取值如表1。

用matlab对模型进行数值仿真，得到各药品的最优订购量，见表2。

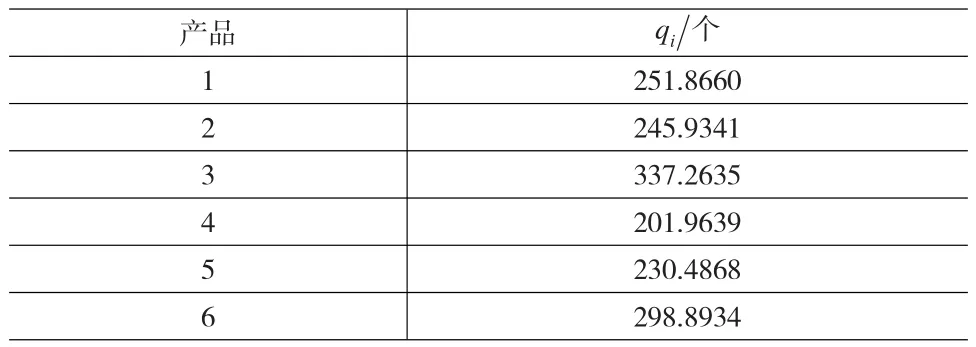
表2 求解结果

总利润Π=2799.0794，所需库存空间W=60.7647

5 总结

本文通过建立库存空间约束模型，研究医院药品一次性联合最优订购量的策略。在模型中，本文假设需求服从指数分布，变质率为常数，且需求与变质率互不影响。在允许缺货和具有提前期的情况下，本文给出了带有库存空间约束的最优订购量模型，并且依据简约梯度法，给出了求解最优订购量的具体算法。最后以六种药品为例进行数值仿真。

本文假定药品之间的需求率和变质率互不影响，且变质率为常数等。这些假设都是为了便于求解模型。而为了使模型更加切合实际，可以对上述假设作进一步改进。如假设变质率不为常数，同药品之间需求率相互影响等。

[1]熊燕华,李风华.基于协同补货策略的医院药品库存管理探讨[J].中国药房,2007,25(18).

[2]凌春燕,方芸.我院药品库存管理模式的实践[J].药学与临床研究,2010,18(4).

[3]Nicholson L,Vakharia A J,Erenguc S.Outsourcing Inventory Management Decisions in Healthcare:Models and Application[J].European Journal of Operational Research,2004,154(1).

[4]马昌凤.最优化方法及其Matlab程序设计[M].北京：科学出版社,2011.