双轴车辆俯仰振动及凸块路面平顺性仿真研究

高 晋，杨秀建，牛子孺， 陈蜀乔

(昆明理工大学 交通工程学院,昆明 650500)

双轴车辆俯仰振动及凸块路面平顺性仿真研究

高 晋，杨秀建，牛子孺， 陈蜀乔

(昆明理工大学 交通工程学院,昆明 650500)

建立了双轴车辆仿真模型，在模型前后轮上加载有时间延迟的正弦波激励以模拟汽车的俯仰振动情况。仿真计算出轴距中心处车身的垂向加速度和俯仰角加速度折算幅频特性曲线。分析幅频特性曲线得出车身纯垂直振动和纯角振动的激励频率以及幅频特性曲线的频率间隔，确定敏感的振动频率。改变样机模型的轴距和前后轮输入的相位差，分析轴距和车速对幅频特性曲线的影响。结果表明：车速减小，轴距变大，幅频特性曲线的频率间隔减小。由垂向加速度和俯仰角加速度幅频特性曲线计算出加速度均方根值，得出沿车身纵轴线方向不同位置的加速度均方根值，为确定最佳座位点提供依据。分析仿真模型通过凸块路面时的加速度均方根值变化量，结果表明：前后脚部地板纵向加速度都是在后轮通过时较大，而前后脚部地板垂向加速度则分别对应前后轮通过时较大。

平顺性；俯仰振动；凸块路面；双轴车辆

双轴车辆系统在路面行驶时，前后轴同时受到激励，这时车身不仅有垂向运动，而且有俯仰运动[1]。此外，前后轮的输入存在相位差，并且前后轮的输入激励相互干涉，此时，车身的响应不仅与悬架的刚度、阻尼因素有关，还与车辆的行驶车速、轴距、激励频率、联系质量等因素相关。当车辆在不平路面上行驶或通过凸块路面时，车身除了有垂向振动外，车轮上还会形成附加的纵向力，它将激励车辆产生纵向振动。文献[2]采用动力学微分方程转化为状态方程的方法分析了车身上任一点垂直加速度和俯仰角加速度对前轮输入的幅频特性。文献[3]在建立8自由度模型的基础上，推导并仿真计算了车身加速度均方根值等平顺性参数。但是，用微分方程建立的仿真模型自由度不多，对实际模型进行了不同程度的简化，分析精度不高。本文通过在ADAMS中建立面向结构的双轴车辆系统模型，利用正弦波激励来研究车辆轴距、车速、激励频率对车身不同位置响应的影响，将车身在前后轮双路输入的响应折算为前轮输入的响应，仿真分析其幅频特性规律及影响因素。同时，仿真车辆模型通过凸块路面的情况，分析对比车身脚底板的垂向和纵向振动。将理论和仿真相结合，探明了双轴车辆车身在不同激励频率下和在凸块路面上的响应特性。

1 双轴车辆振动系统幅频特性分解计算

图1为双轴汽车振动等效模型[4]。由于车辆是对称的，所以也叫半车辆模型。后轮行驶在前轮的轮辙上，所以前后轮的不平度激励除了轴距引起的相位差之外都是一样的，因此也叫单轮辙激励[5]。

图1 单轮辙激励的双轴汽车振动模型

图1中，车身上任一点P到前轴距离为l，轴距为L。因此，在前轮处l/L=0,在后轮处l/L=-1,在轴距中心处l/L=-0.5。P点的垂直位移z2p与前、后轴上方的垂直位移z2f，z2r的关系为

(1)

前后车轮在同一车辙上行驶，则两个路面不平度函数只存在一个时间滞后量Δt=L/u，它取决于轴距L和车速u，此时前后轮的路面输入之间的关系是

(2)

复振幅之间的关系为

(3)

前轮上方车身位移的复振幅可表示为：

(4)

(5)

后轮上方车身位移的复振幅可表示为

(6)

由以上公式可以看出：对于前后轮上方的位移响应，双轮激励相当于前轮单点激励。对于其他任一点位置可根据式(1)得出，因此，前后轮双输入可等效为前轮单输入。

基于此，在分析前、后轮双输入振动系统在路面输入下的随机响应时，可以通过前后轮路面输入的关系，把车身上任一点的响应转化为只求它们对前轮输入的响应，即把双轮输入的响应折算为单轮输入的响应。

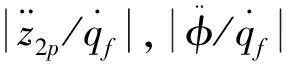
(7)

(8)

现分析车身上任一点p的情况。车身前后轴上方的垂直位移z2f，z2r存在以下的关系：

(9)

代入式(1)得出：

(10)

所以车身上任一点的垂直位移对前轴上方车身位移的幅频特性为

(11)

在纯垂直振动时，前后轮输入相位差ωΔt=0,2π,4π,6π…，车身各点幅频特性 |z2p/z2f|=1，车身各点垂直位移相同。在纯角振动时，前后轮输入相位差ωΔt=0,π,3π,5π…，根据式(11)，|z2p/z2f|=1+2l/L。在轴距中心处，l/L=-0.5，|z2p/z2f|=0，没有垂直方向的位移；在轴距中心与前后轴之间l/L=-0.25，-0.75处，|z2p/z2f|=0.5；在前后轴上方l/L=0,-1处，|z2p/z2f|=1；在轴距外l/L=0.25,-1.25处，|z2p/z2f|=1.5。因此可以看出，纯角振动时，到轴距中心的距离越远，垂直振动位移越大。

2 轴距中心处车身垂直加速度和俯仰角加速度幅频特性仿真

在一定轴距L和车速u下，前后轮响应的相位差ωΔt与激振频率ω的关系为

(12)

所以相位差ωΔt随ω变化的斜率与轴距成正比，与车速成反比，因此对于不同轴距和车速，车身响应的幅频特性也将不同。

图2 双轴车辆仿真模型

以下将分析轴距L为2.5m、车速u为12.5m/s时轴距中心处的车身垂向加速度和俯仰角加速度幅频特性。

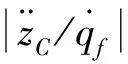
图C和对f的折算幅频特性)

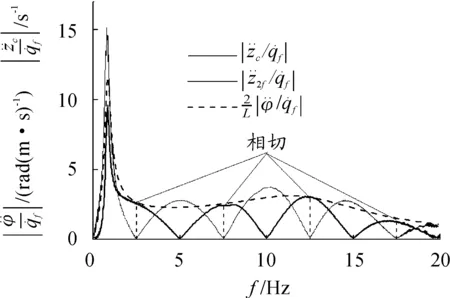
图C和对f的折算幅频特性

折算幅频特性花环状曲线花瓣的间距由Δω确定。Δω表示前后轮输入的相位差ωΔt等于2π时相应的频率间隔，因此

对于轴距L为2.5 m、车速u为12.5 m/s的情况，频率间隔(即花瓣曲线间隔)为

如果能调整相位差和前后轮输入频率ω的关系，就可以改变折算幅频特性花环状曲线的形状。

由式(12)可见：轴距L加长或者车速u降低都会使相位差ωΔt随ω变化的斜率加大，即产生纯垂直振动、纯角振动的频率间隔Δω变窄。反之，L变短或者u提高会使Δω变宽。

3 车速对车身垂直加速度和俯仰角加速度幅频特性影响分析

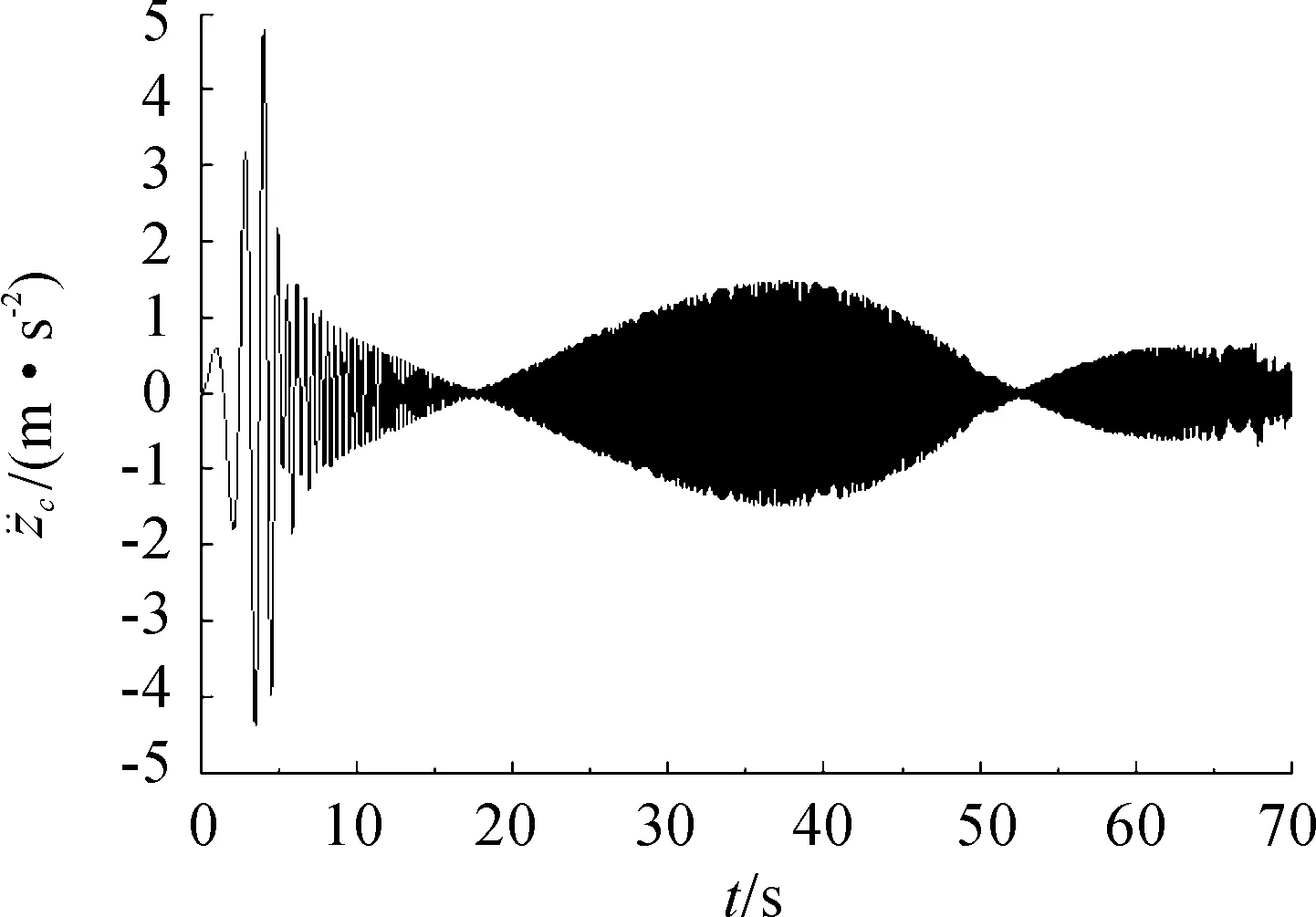
图5 u=25 m/s时的加速度时间历程曲线

图6 u=25 m/s时的垂向加速度幅频特性曲线

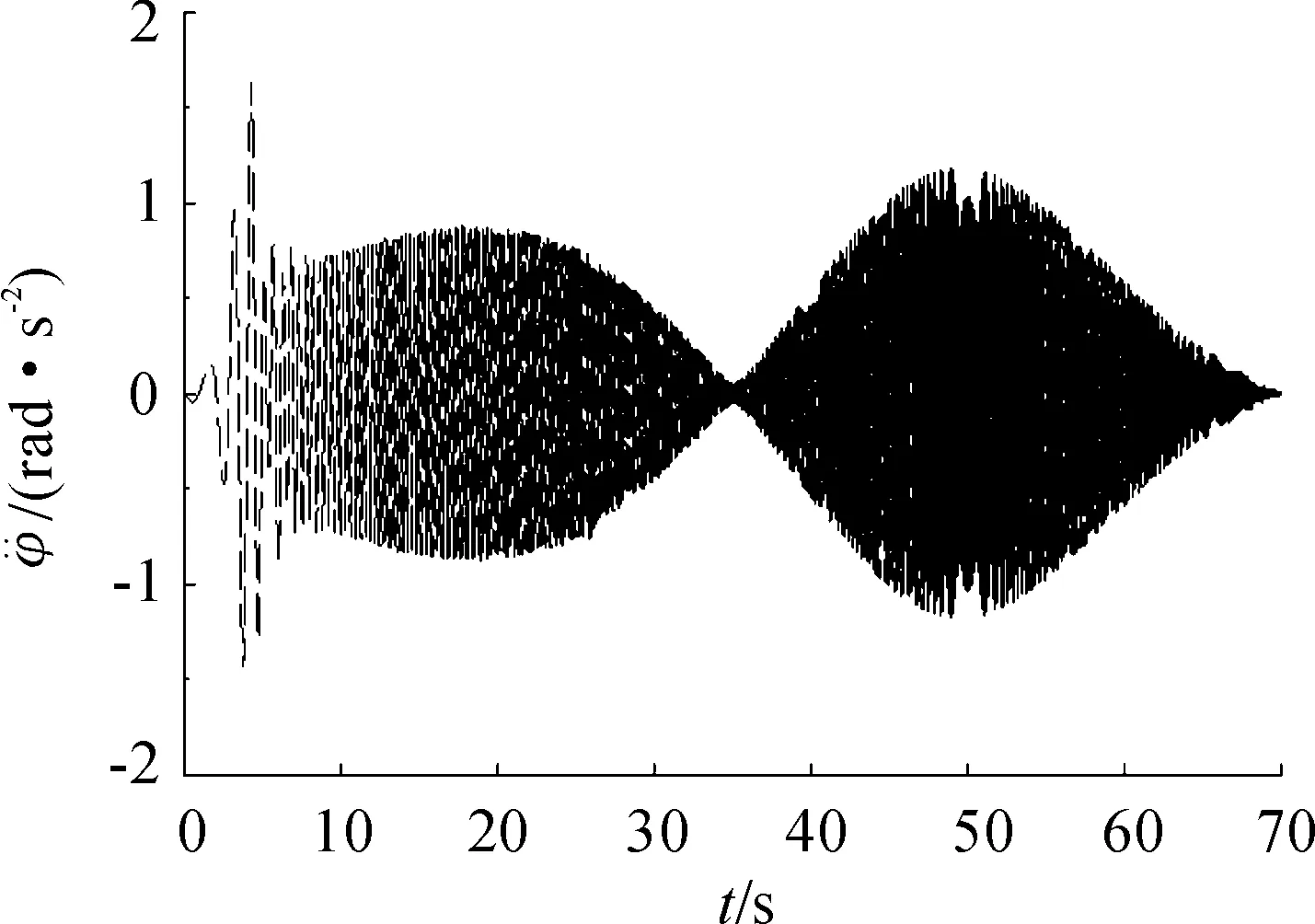
图7 u=25 m/s时的俯仰角加速度时间历程曲线

图8 u=25 m/s时的俯仰角加速度幅频特性曲线

根据本文分析，在轴距L为2.5 m，车速u为25 m/s时，前后轮相位差等于2π的频率间隔(即花瓣的曲线的间隔)为

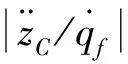
图9 u=8.3 m/s时的加速度幅频特性曲线

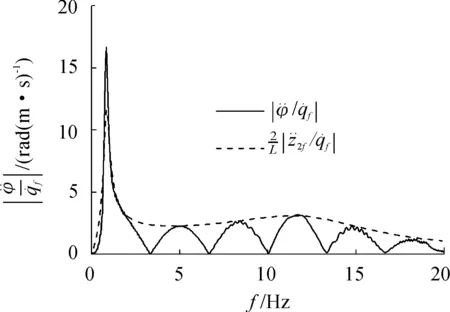
图10 u=8.3 m/s时的俯仰角加速度幅频特性曲线

根据分析，在轴距L为2.5 m、车速u为8.3 m/s时，前后轮相位差等于2π的频率间隔，也即花瓣曲线的间隔为

对比车速u为25，12.5，8.3 m/s时的仿真分析结果可以看出：随着车速减小，幅频特性曲线的花瓣间距会减小，也即频率间隔Δf减小，这与理论分析的结果一致。

4 轴距对车身垂直加速度和俯仰角加速度幅频特性影响分析

如前所述，改变轴距也将改变前后轮的输入相位差ωΔt，因此下面将分析轴距的改变对于垂向加速度和俯仰角加速度幅频特性的影响。

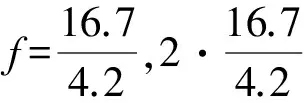
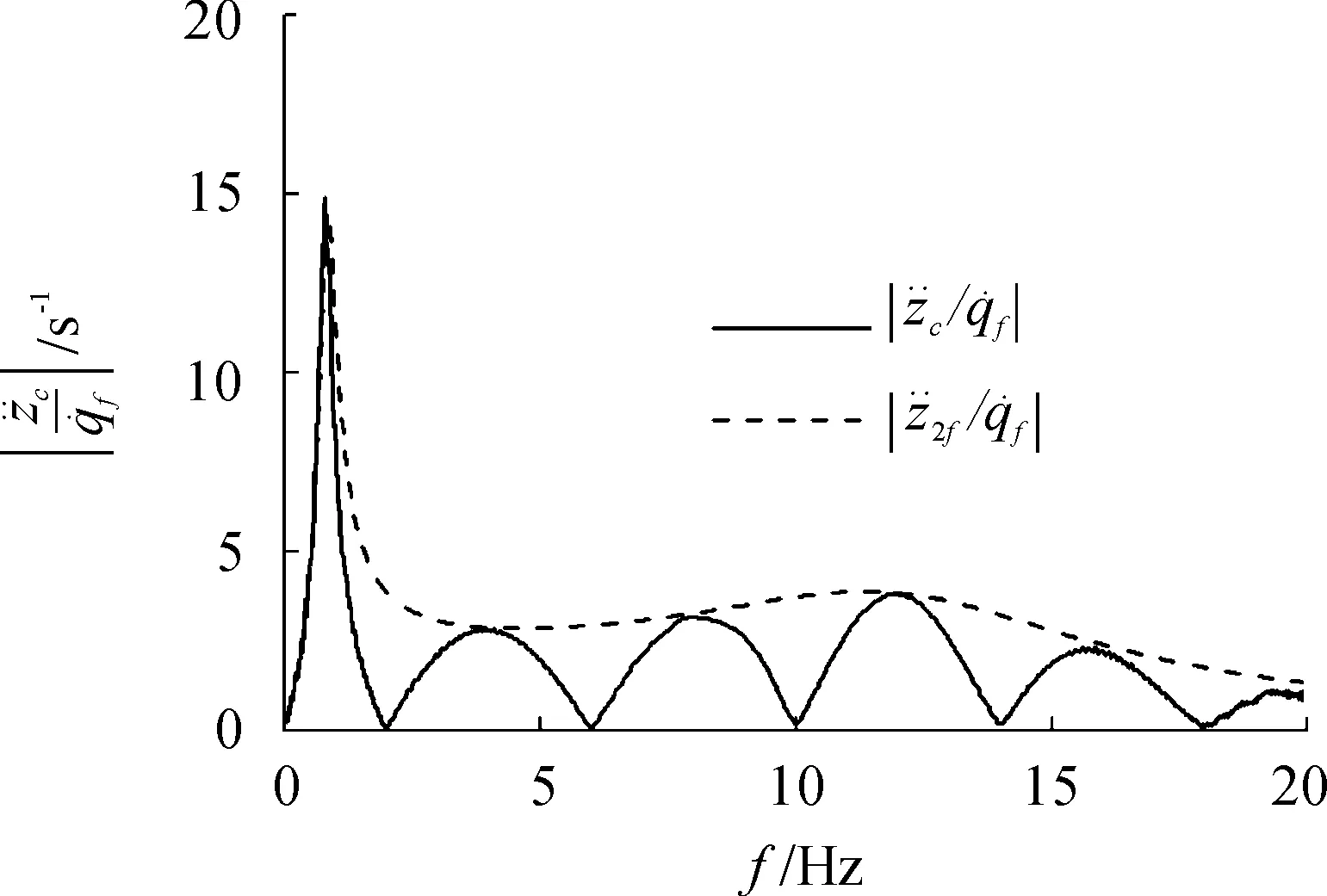
图11 L=4.2 m，u=16.7 m/s时垂向加速度幅频特性

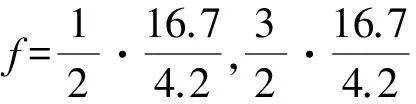
轴距L为4.2 m时，花瓣曲线的间隔为

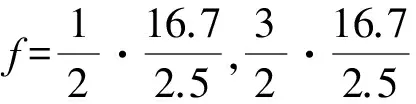
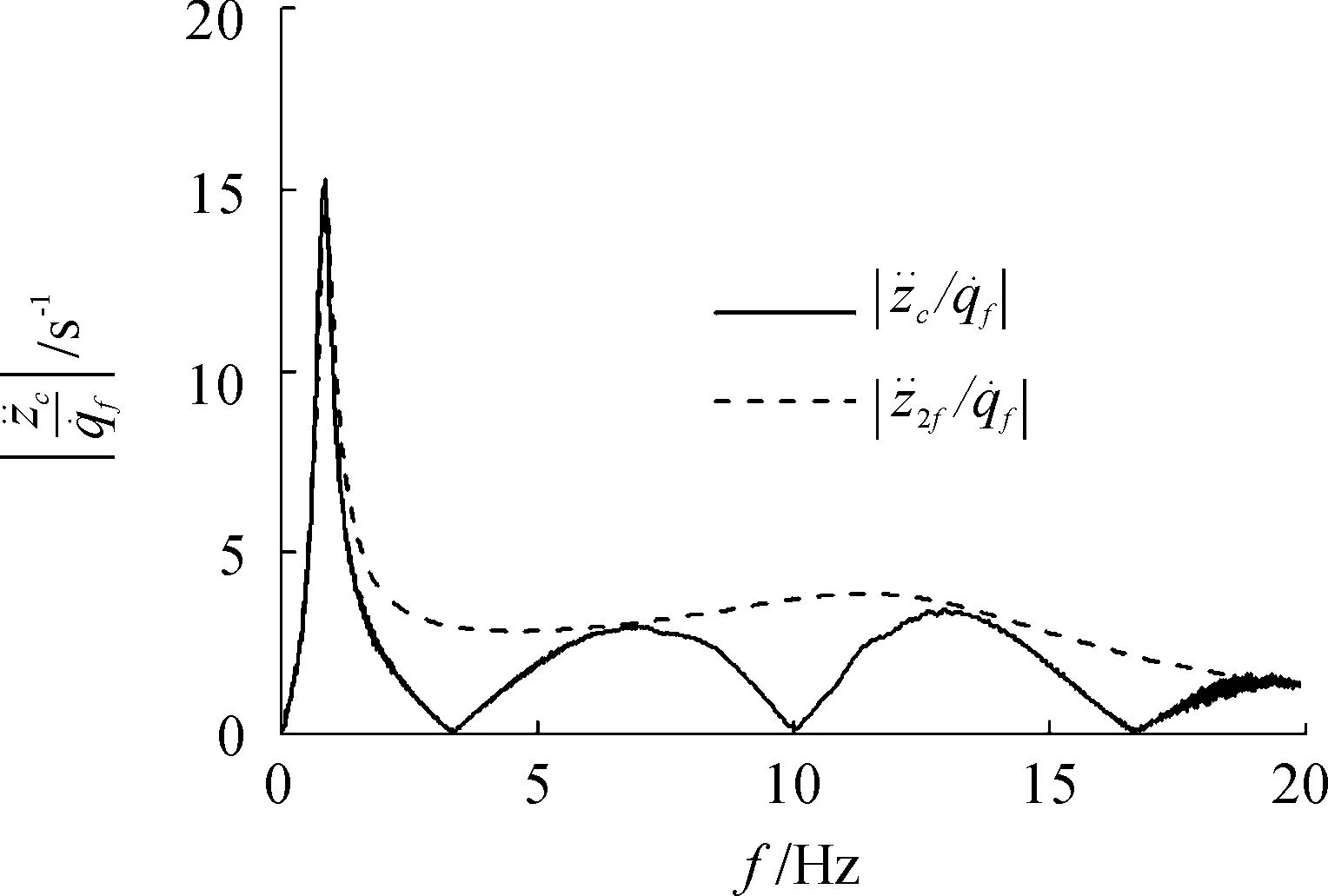
图13 L=2.5 m，u=16.7 m/s时垂向加速度幅频特性

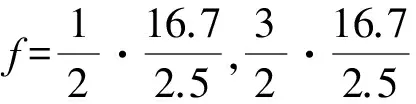
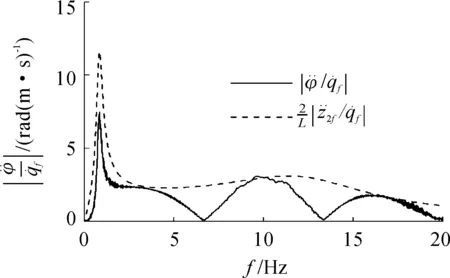
图14 L=2.5 m，u=16.7 m/s时垂向加速度幅频特性

轴距L为2.5 m时，花瓣的曲线的间隔为

从轴距为4.2，2.5 m时的仿真分析结果可以看出：随着轴距增大，幅频特性曲线的花瓣间距会减小，也即频率间隔Δf会减小，这与理论分析的结果一致。

5 车速和轴距对车身加速度、角加速度均方根值的影响

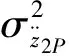
图15是车速u=20 m/s时仿真得到的沿车身纵轴不同位置的垂向加速度均方根值与轴距的关系曲线。从图中可看出，随着轴距加长，在l/L=0,-1处(即前后轴上方处)车身加速度均方根值没有影响，但使轴距内位置l/L=-0.25，-0.75和l/L=-0.5处的车身加速度均方根值略有下降，使轴距外位置l/L=0.25,-1.25处车身加速度均方根值略有上升。另外，在l/L=-0.25，-0.75处与l/L=-0.5处的均方根值比较接近，这说明在汽车轴距中心附近大约半个轴距范围内垂直加速度均方根值变化不大。

图17、18分别是是轴距L=2.5 m时沿车身纵轴不同位置的垂向加速度均方根值和车身角加速度均方根值与车速的关系曲线。可以看出，所有位置的垂向加速度均方根值和角加速度均方根值都随车速加大而上升。图中加速度、角加速度均方根值与车速不是完全的线性关系，这主要是由于车速使折算幅频特性花环状曲线形状发生改变所致。

图15 不同位置加速度均方根值随轴距变化的比较

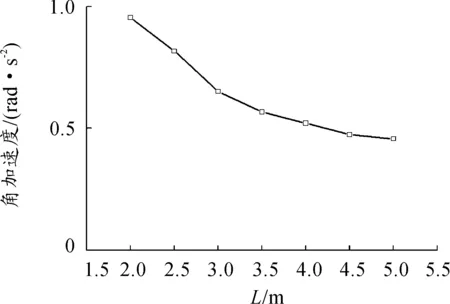
图16 车身角加速度均方根值与轴距的关系曲线

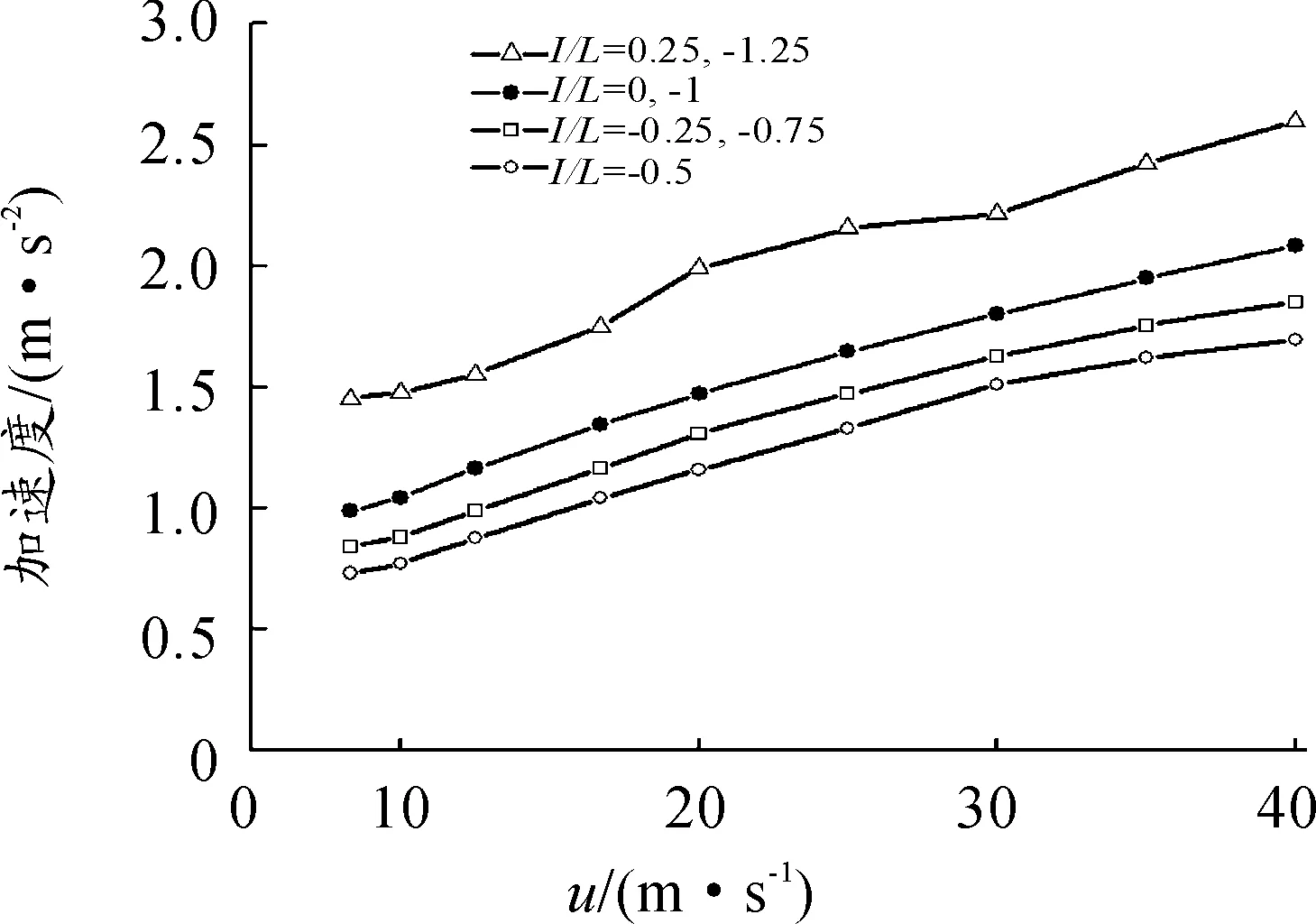
图17 不同位置加速度均方根值随车速变化的比较

图18 车身角加速度均方根值与车速的关系曲线

6 凸块路面仿真分析

如本文所述，双轴车辆通过凸块时，由于前后轮相继通过，因此前后轮的输入有一个相位差，车身的运动受前后轴输入的干涉影响[11-12]。 让整车仿真模型通过凸块路面，凸块高为25 mm，如图19所示，这时车身上任一点的加速度时间里程曲线会有两个峰值。图20为脚底板位置。

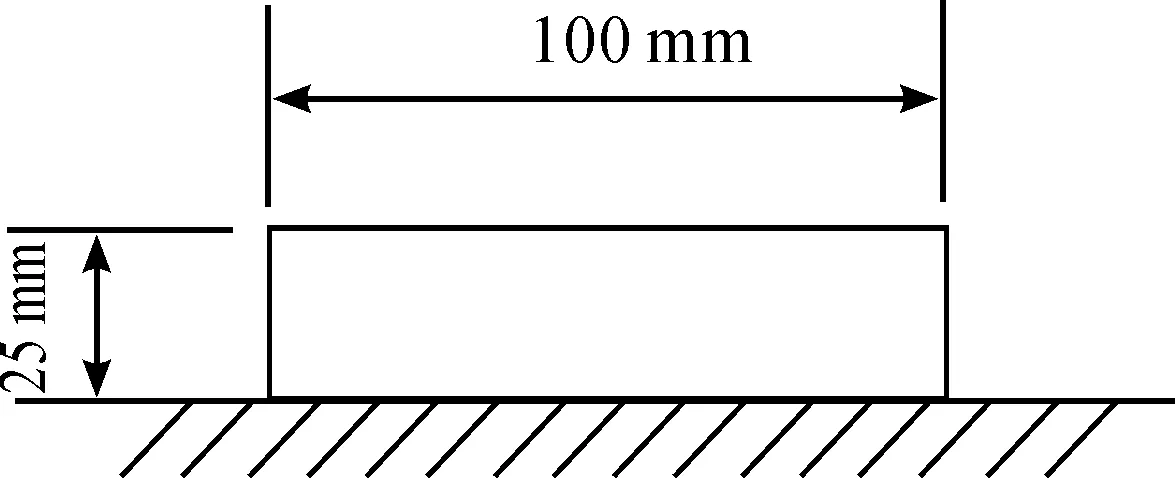
图19 凸块尺寸

图20 脚底板位置

图21、22分别是加速度均方根值局部变化量ΔRMSLoc和加速度均方根值全局变化量ΔRMSGlob的意义。ΔRMSLoc在计算时选用小的窗函数，这样计算出的均方根曲线也有两个峰值。ΔRMSLoc是车辆通过凸块后的均方根值最大峰值与通过凸块前的均方根值之差。ΔRMSGlob在计算时选用大的窗函数，ΔRMSGlob是车辆通过凸块后的均方根值峰值与通过凸块前的均方根值之差。

图23、24分别是模型仿真测量得到的车身前脚底板的纵向和垂向加速度时域信号Signal(图20)[13-15]、加速度均方根值局部变化量ΔRMSLoc、加速度均方根值全局变化量ΔRMSGlob。从ΔRMSLoc的两个峰值可以看出：前脚部地板纵向加速度在后轮通过时较大，而垂向加速度在前轮通过时较大。

图21 ΔRMSLoc

图22 ΔRMSGlob

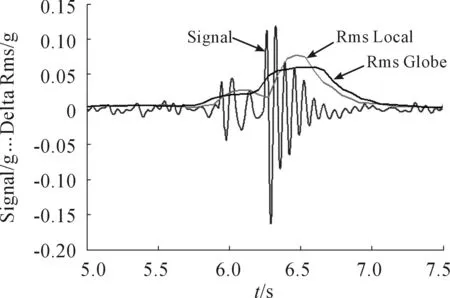
图23 前脚部地板纵向加速度时域信号

图24 前脚部地板垂向加速度时域信号

图25、26分别是模型仿真测量得到的车身后脚底板的纵向和垂向加速度时域信号Signal、加速度均方根值局部变化量ΔRMSLoc、加速度均方根值全局变化量ΔRMSGlob。从ΔRMSLoc的两个峰值可以看出：后脚部地板纵向加速度也是在后轮通过时较大，而垂向加速度则是在后轮通过时较大。

图25 后脚部地板纵向加速度时域信号

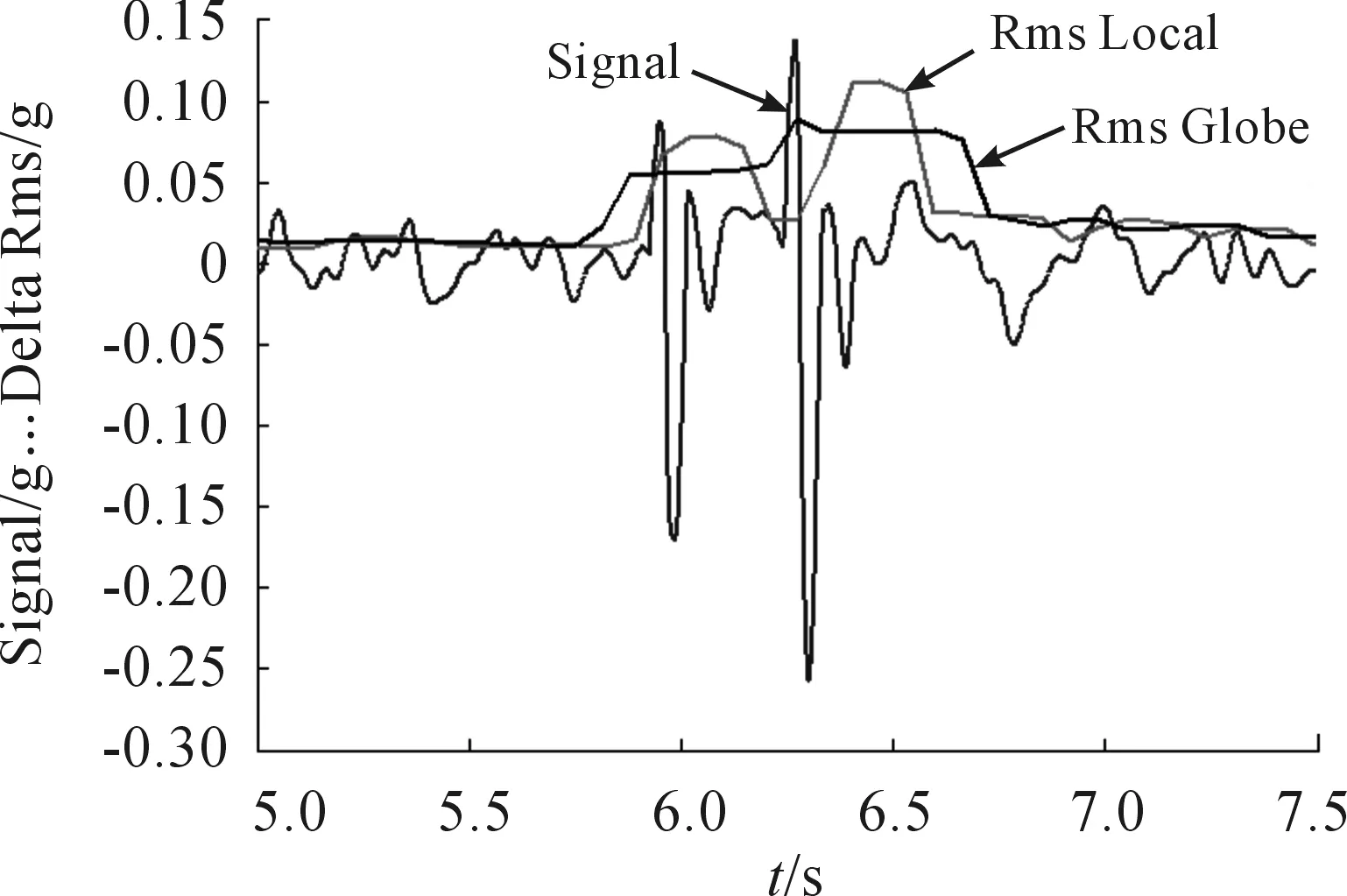
图26 后脚部地板垂向加速度时域信号

图27是通过凸块路面时前后脚底板垂向和纵向加速度均方根值的比较，可以看出对于垂向加速度均方根值，前脚部地板大于后脚步地板，对于纵向加速度均方根值，后脚步地板略大于前脚部地板。

7 结论

1) 建立样机模型，在样机模型前后轮上加载有时间延迟的正弦波激励可方便地模拟汽车的俯仰振动情况。由于双轴车辆在路面行驶时前后轮的输入只相差一个相位，因此可将双轮输入的车身响应折算为前轮单输入的车身响应。通过仿真计算出轴距中心处车身垂向加速度和俯仰角加速度对前轮输入的幅频特性曲线。分析幅频特性曲线能得出车身纯垂直振动和纯角振动的激励频率以及频率间隔。采用同样方法可分析车身上任一点对前轮输入的幅频特性曲线，从而可方便地研究车身沿纵向不同位置敏感频率分布情况。

图27 前后脚部地板垂向和纵向加速度均方根值比较

2) 由于前后输入的相位差与车速和轴距相关，因此通过改变样机模型的轴距和前后轮输入的相位差可分析轴距和车速对幅频特性曲线的影响。随着车速减小，轴距变大，幅频特性曲线的花瓣间距也会减小，也即频率间隔Δf减小。因此，调整轴距可改变垂直振动和俯仰振动的频率结构，从而避开敏感的振动频率范围。

3) 由垂向加速度和俯仰角加速度幅频特性曲线可得出沿车身纵轴线方向不同位置的加速度均方根值，从而为确定最佳座位点提供依据。

4) 仿真模型通过凸块路面时，通过分析加速度均方根值变化量可看出，前后脚部地板纵向加速度都是在后轮通过时较大，而前后脚部地板垂向加速度则分别对应前后轮通过时较大。

[1] 杨波，王学林，胡于进，等.多轴汽车平顺性的柔性模型研究[J].机械工程学报，2003,39(12):145-150.

[2] 黄治潭，张孝祖，乐巍.汽车一般双轴悬架模型及其平顺性分析[J].江苏大学学报：自然科学版，2003,24(1):52-54.

[3] 黄志刚，毛恩荣，梁新成，等.微型轿车八自由度整车动力学仿真与试验[J].农业机械学报，2008,39(6):28-32.

[4] 张孝祖，乐巍.分析双轴汽车模型平顺性的推广方法[J].江苏大学学报：自然科学版，2002,23(3):41-44.

[5] M.米奇可.汽车动力学[M].4版.北京，清华大学出版社，2003:336-376.

[6] 李杰，秦玉英，赵旗，等.虚拟激励法及其在汽车随机振动应用中的探讨[J].汽车技术，2007(7):24-27.

[7] 徐中明，周小林，余峰，等.汽车平顺性分析的时域和频域法的对比[J].汽车工程，2012,34(4):306-310.

[8] 张洪信，陈秉聪，张铁柱，等.车辆纵振路面谱研究[J].汽车工程，2002,24(6)：513-515.

[9] 王岩松，段敏，耿艾丽，等.车辆人体振动系统的时域模拟及频谱分析[J].吉林大学学报，2004，34(3):373-377.

[10]王乾廷，伊启中，林永南.越野路面不平度与车轮跳离路面量间的关系[J].系统仿真学报，2008,20(11):3040-3042.

[11]John B F.Characterising road profiles as Markov Chains[J].International Journal of Vehicle Design,2004,36(2/3):103-115.

[12]ELS P S.The applicability of ride comfort standards to off-road vehicles[J].Journal of Terramechanics,2005(12)：4898.

[13]Meada S,Manafield N J,Shibata N.Evaluation of Subjective Responses to Whole-body Vibration Exposure:Effect of Frequency Content[J].International Journal of Industrial Ergonomics,2008 ,38(5/6):1-7.

[14]ZHANG lijun,LEE Changmyung,WANG Yangsong.A study on nonstationary random vibration of a vehicle in time and frequency domains[J].International Journal of Automotive Technology,2002,13(3):101-109.

[15]孙中辉，李幼德，孙中红，等.改进的车辆平顺性模型[J].吉林大学学报，2008，38(3):497-503.

(责任编辑 刘 舸)

Analysis of Pitching Vibration and Bump Road Ride Comfort About Double Axles Vehicle

GAO Jin, YANG Xiu-jian, NIU Zi-ru, CHEN Shu-qiao

(Faculty of Transportation Engineering, Kunming University of Science and Technology, Kunming 650500, China)

A double axles vehicle model with was established. Pitching vibration was simulated by loading Sine wave excitation with time delay on front and rear wheel of the model. The conversion amplitude-frequency characteristics curve of vertical acceleration and pitching angular acceleration in the middle of wheelbase were computed. The amplitude-frequency characteristics curves were analyzed, finding out excitation frequency of exclusive vertical and pitching vibration and frequency interval of the curves to ascertain sensitive vibration frequency. With the changing wheelbase of the model and phase difference, we studied the influence of wheelbase and speed on the amplitude-frequency characteristics curves. The results show that reducing speed and lengthening wheelbase will increase frequency interval of the amplitude-frequency characteristics curves. Computing acceleration Rms of body at different longitudinal position by amplitude-frequency characteristics curves of vertical acceleration and pitching angular acceleration can provide design reference of optimal seat position. According to simulation analysis results of acceleration Rms of front and rear floor, longitudinal acceleration of front and rear floor is larger when rear wheel passing, but larger vertical acceleration of front or rear floor is separately when corresponding front wheel or rear wheel passing.

ride comfort; pitching vibration; bump road; double axles vehicle

2015-05-06 基金项目：国家自然科学基金资助项目(51465023)；昆明理工大学校人才培养项目(省级)(KKSY201402065)

高晋(1982—)，男，博士，讲师，主要从事汽车系统动力学研究。

高晋，杨秀建，牛子孺， 等.双轴车辆俯仰振动及凸块路面平顺性仿真研究[J].重庆理工大学学报：自然科学版，2015(9):20-29.

format：GAO Jin, YANG Xiu-jian, NIU Zi-ru, et al.Analysis of Pitching Vibration and Bump Road Ride Comfort About Double Axles Vehicle[J].Journal of Chongqing University of Technology:Natural Science，2015(9):20-29.

10.3969/j.issn.1674-8425(z).2015.09.004

U463.33

A

1674-8425(2015)09-0020-10