基于LQG-PID的EPS系统最优控制

邵宪友,李志鹏,杨传英，李晓英

(东北林业大学 交通学院，哈尔滨 150040)

基于LQG-PID的EPS系统最优控制

邵宪友,李志鹏,杨传英，李晓英

(东北林业大学 交通学院，哈尔滨 150040)

汽车电动助力转向(EPS)系统因受系统本身模型参数不确定性、路面随机激励和转矩传感器的测量噪声等干扰因素的影响，使用传统PID控制方法已不能满足对其精确控制的要求。通过构建EPS系统的数学模型，并加入随机干扰信号，建立系统的状态空间表达式，在PID控制的基础上设计线性二次型高斯(LQG)状态反馈控制器,即优化的LQG-PID控制。以能耗最小为目标函数，运用Matlab/Simulink对EPS系统进行仿真分析。仿真曲线表明:应用LQG-PID控制方法能有效减小系统受到的随机干扰，使能耗及电动机的实际助力电流与目标电流的误差最小，提高了EPS系统的鲁棒性。

电动助力转向系统；PID控制；LQG-PID控制器；最优控制

电动助力转向系统(electric power steering system， EPS)通过ECU接收力矩信号和车速信号，并经运算处理后向电动机发出控制指令，使电动机通过输出一个转矩来提供转向助力，减小驾驶员操纵力,进而提高汽车转向的轻便性和灵活性[1-2]。汽车EPS技术是一项低能耗、低污染，有利于能源的节约和环境保护，紧扣现代汽车产业发展趋势的高新技术，其研究具有重大现实意义。但因EPS系统存在着较复杂的非线性因素的干扰( 例如来自道路路面的随机干扰、EPS模型参数输入的不确定性以及传感器产生的测量噪声等)，应用传统PID控制已不能满足其控制要求。为解决这个问题，需要采用现代最优控制理论。此理论是一种运算精确的数学解析方法,可对EPS系统性能指标进行最优化,使系统性能达到所需要求。在以现代控制理论方法为基础的理论研究中,较常见且又有效的控制设计方法是线性系统二次型性能指标高斯分布法(linear quadratic Gaussian,LQG)。LQG最优控制实质上是以能耗及电机输出的实际助力电流与目标电流之间的误差最小为控制系统的性能指标，使EPS系统对输入参数的变化不敏感，进而使其具有较强的抗干扰性，即较好的鲁棒性。

本文首先建立EPS系统的数学模型，并加入随机干扰信号，建立系统的状态空间表达式，以能耗最小为目标函数，在PID控制的基础上设计LQG最优控制器,即优化的LQG-PID控制。采用双闭环控制,内环应用LQG优化控制,外环应用PID控制方法,从而降低 EPS系统受到的非线性因素所引起的干扰。

1 EPS系统数学模型的建立

汽车EPS是主要由扭矩传感器、车速传感器、电动机、减速机构、电机控制单元(ECU)及控制策略等组成，是一种直接通过电机提供辅助扭矩的动力转向系统，其结构如图1所示。

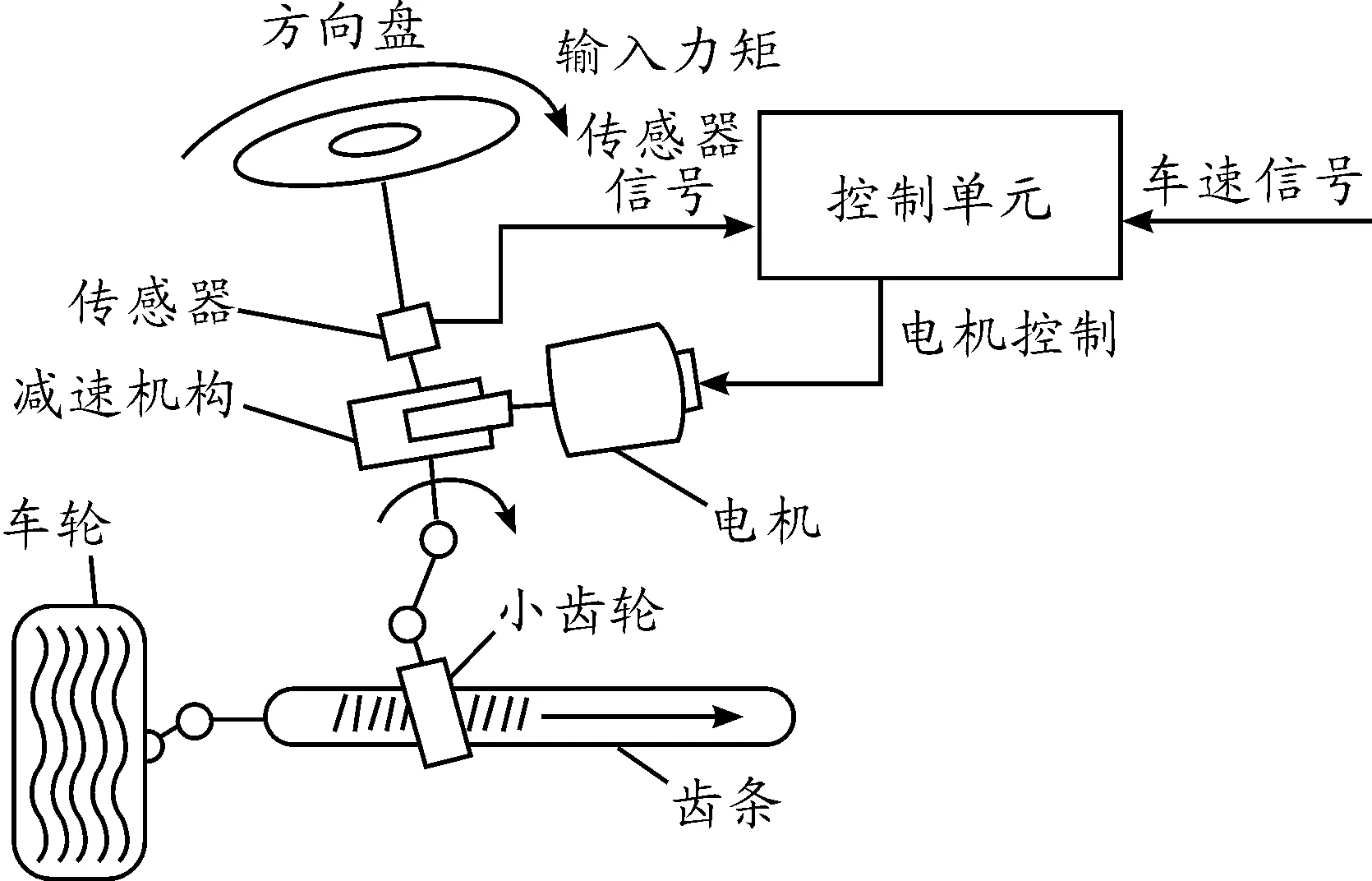
图1 EPS结构

1.1 EPS系统的数学模型

对组成电动助力转向系统的转向管柱、助力电机和齿条分别进行受力分析，并将系统中阻尼的非线性部分忽略，得到转向管柱、齿条和电机的数学模型[3]:

(1)

(2)

(3)

(4)

(5)

(6)

式(1)～(6)中:kc为转矩传感器扭杆刚度;Jc为方向盘、转向管柱的等效转动惯量；bm为电机轴和蜗杆总成等效阻尼系数;bc为转向管柱阻尼系数;Jm为电机轴转动惯量;m为齿条质量；br为齿条阻尼系数:kr为等效弹簧刚度;G为减速器的减速比;θc为方向盘转角;km为减速机构和助力电机枢轴等效刚度系数;Td为方向盘输入转矩;θm为电机转角;xr为齿条位移;rp为小齿轮半径:ke为电机反电势系数；L为电机电感;u为电机控制电压;R为电机电枢电阻。

1.2 EPS系统的状态空间方程

(7)

假定各个状态变量为

式中a是由助力特性曲线(图2)中所测方向盘转矩Td与电动机的目标电流im之间的关系得出：im=a(Td-T0),其中T0=1 N·m。

将各变量代入式(1)～(6)，得EPS系统的状态方程为:

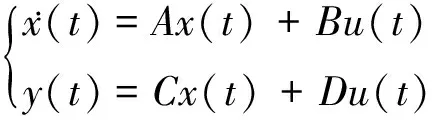
(8)

式中：A为

B为

D=0

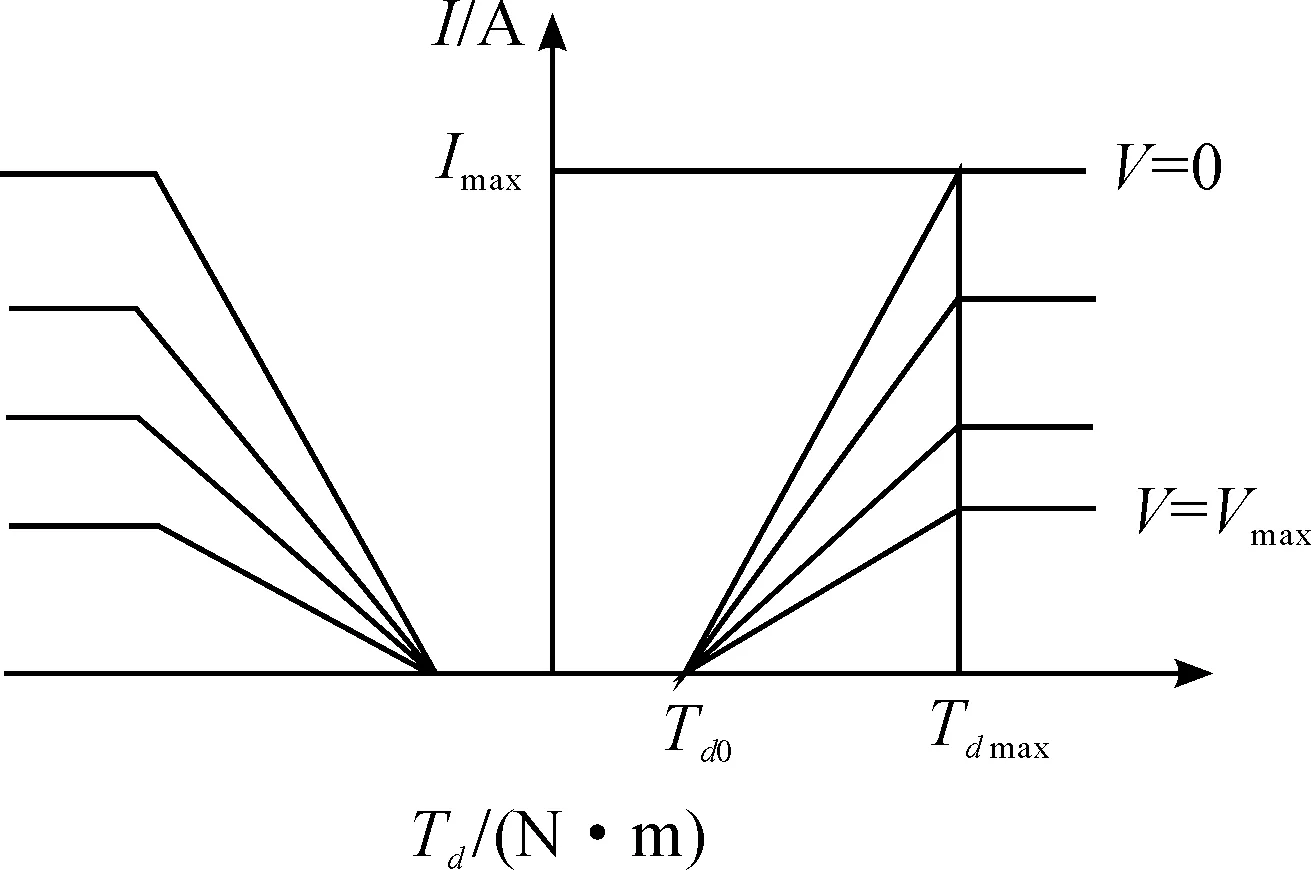
图2 电动助力特性曲线

2 LQG-PID最优控制

2.1 常规PID控制

PID控制[4]又称为比例积分微分控制，实际上是属于线性控制的一种，它是依据输入系统的偏差值，再按照比例、微分与积分函数关系来运算，并将计算结果的加权和作为系统的控制量对受控对象施加控制，其原理如图3所示。

图3 PID控制系统原理

首先由标准值r(t)与实际输出值c(t)组成系统的控制偏差e(t)=r(t)-c(t)。再将偏差的比例值P、积分值I与微分值D线性组合来构成控制量，对受控对象施加控制，其控制规律为

(9)

式中：Kp为比例系数；Ti为积分时间常数；Td为微分时间常数。

2.2 LQG-PID最优控制

EPS系统会受一些不确定性因素影响，例如来自道路路面的随机干扰、EPS模型参数输入的不确定性以及传感器产生的测量噪声等。然而LQG最优控制[5]可以使EPS系统对输入参数的变化不敏感，从而使系统具有较强的抗干扰性，即较好的鲁棒性，所以在PID控制的基础上设计了LQG最优控制器,即优化的LQG-PID控制，以能耗最小为目标函数，采用双闭环控制,内环应用LQG优化控制,外环应用PID控制方法,从而降低了EPS系统受到的非线性因素所引起的干扰。控制结构如图4所示。

设EPS系统的状态空间表达式为:

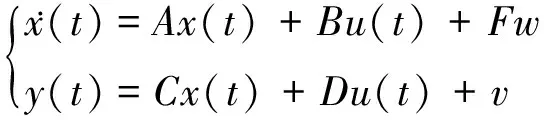
(10)

式中：v为输入的测量噪声；w为输人的系统路面随机干扰。

w和v为已知方差、协方差和零均值的高斯白噪声，两参数的统计特性规律为:

(11)

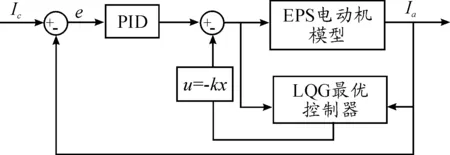
图4 LQG-PID控制结构

以助力电流误差最小为目标函数的LQG控制器的性能指标为

(12)

式中I为实际助力电流。在式(12)的平方和中，以u为基准，将其系数取l，q为助力电流产生误差时的加权系数。为得到合适的q，应在仿真中进行调试后确定。由最优控制理论原理，将式(12)转化为标准二次型形式:

其中Q为

F=[0 0 0 0 1 0 0]T

R=1

由控制系统的状态方程可以构建出一个系统的最优状态估计器，即卡尔曼(Kalman)滤波器,最优估计器方程的表示方法如下：

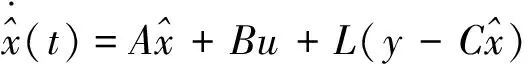
(13)

卡尔曼[6]滤波增益矩阵为

(14)

其中P0满足黎卡提[7](Riccati)方程:

(15)

在状态估计计算时先用卡尔曼滤波理论求得的状态最小方差的估计量，式中L是Kalman滤波器的增益矩阵。在得到状态估计后，再与最优控制以串联的形式形成反馈回路，对其进行控制，最优控制规律为

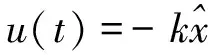
(16)

其中最优反馈增益矩阵k由下式得到:

k=R-1BTP

(17)

式中P满足下列黎卡提(Riccati)方程:

(18)

LQG闭环最优控制器的计算由完全独立的两部分来完成:第1部分是按照最优估计器的计算式(13)～ (15)来求得状态估计，其中卡尔曼滤波器矩阵L可以通过Matlab软件工具箱中lqe命令求得,其程序格式为

L=lqe(A,F,C,Q0,R0)

其中Q0=R0=1。第2部分是按照式(17)、(18)来求得最优反馈增益矩阵k。矩阵k可以通过Matlab软件工具箱中lqr命令求得,其程序格式为

k=lqr(A,B,Q,R)

3 Matlab/Simulink建模及仿真分析

3.1 EPS系统的Matlab/Simulink建模

汽车EPS系统模型包括机械转向系、控制器和电机模型，机械转向系模型由转向管柱和齿条模型组成。在Matlab/Simulink中建立EPS系统各组成部分模型，转向管柱和齿条模型如图5、6所示，电机模型如图7所示，机械转向系和电机的整体模型如图8所示，控制器模型如图9所示，图中的助力特性曲线见图2。模型中：Td为方向盘的输入转矩；Ts为转矩传感器测量值；I为电动机的实际助力电流；Um为电动机的控制电压。外环PID控制模型如图10所示，内环LQG最优控制结构如图11所示。

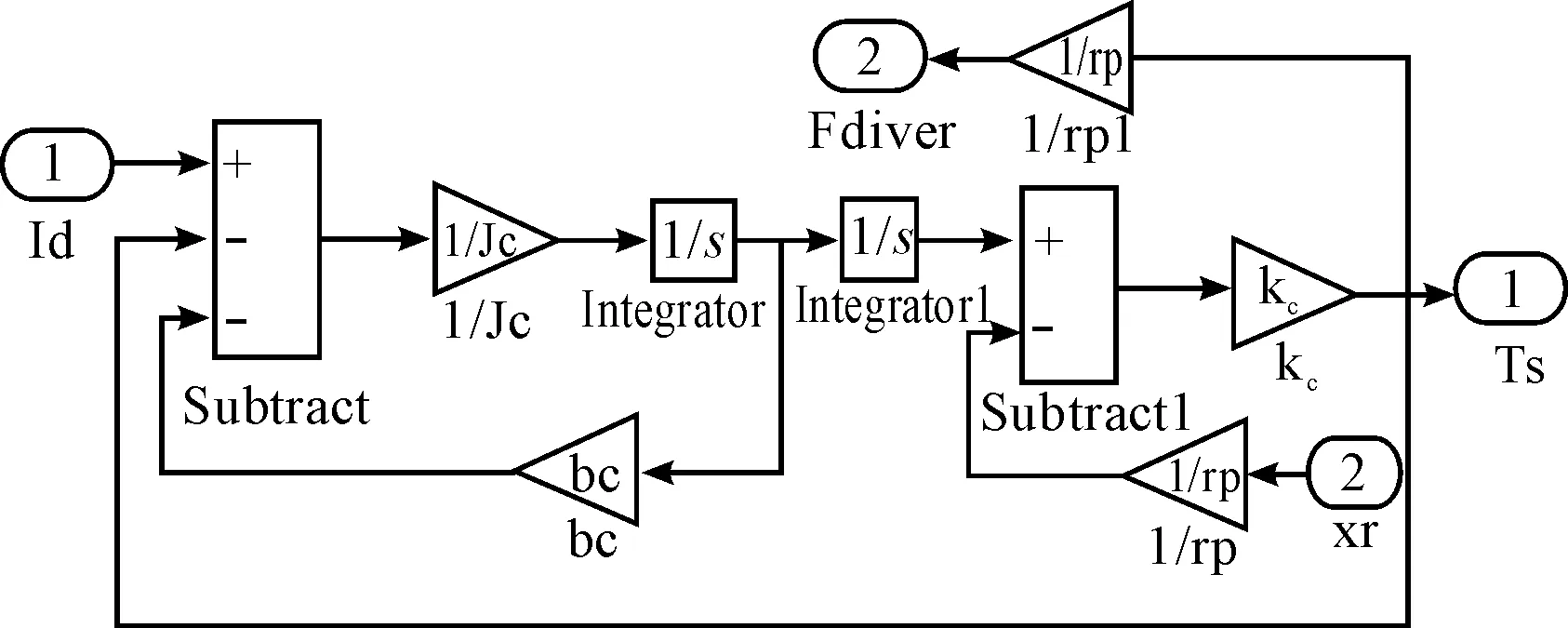
图5 转向管柱模型

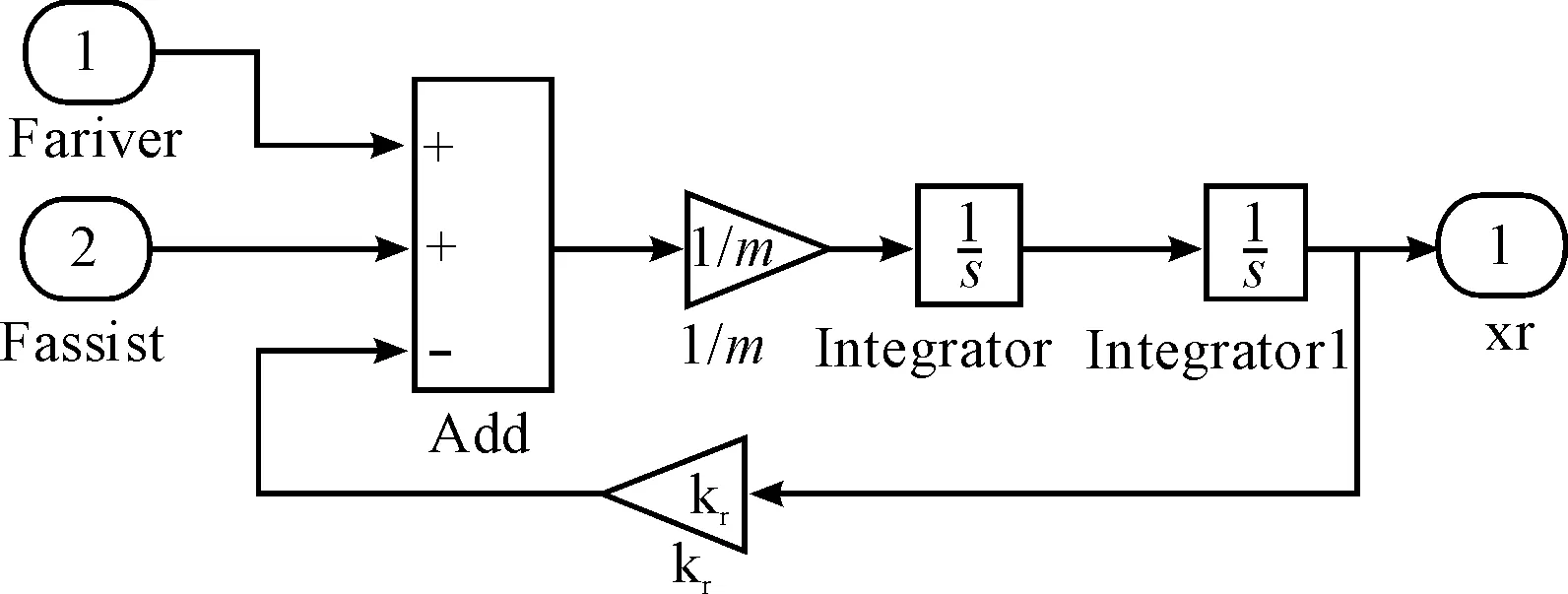
图6 齿条模型

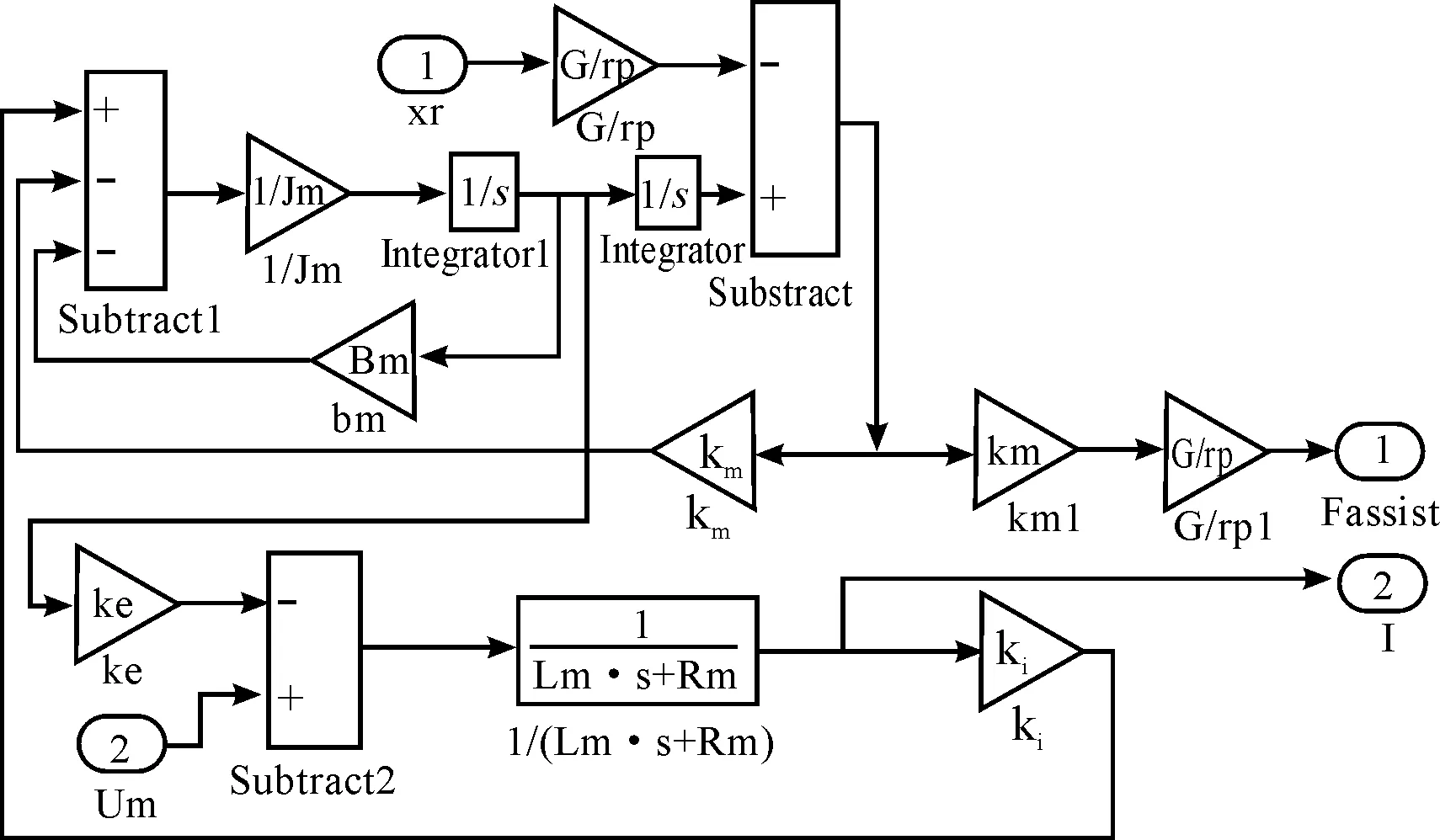
图7 电机模型

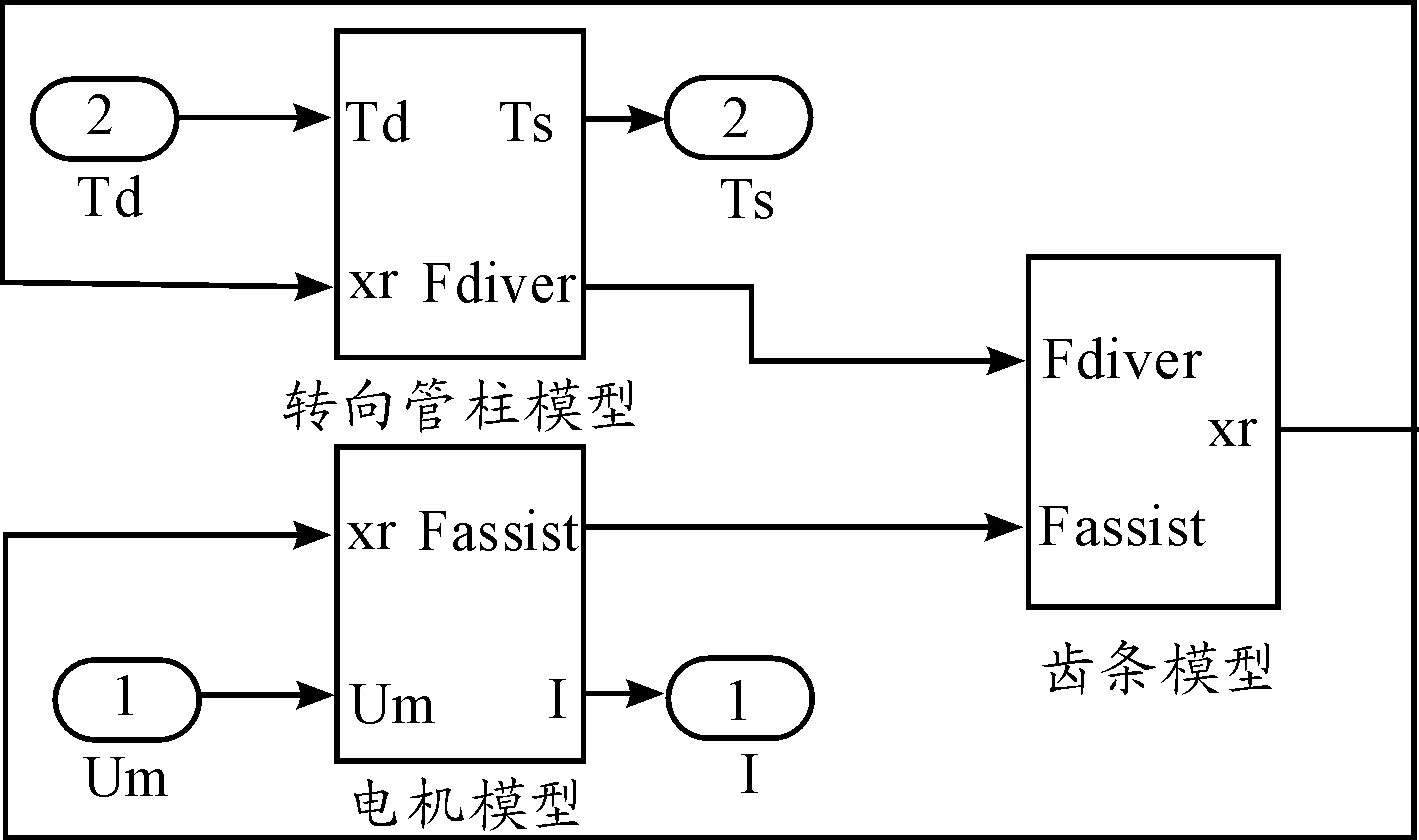
图8 机械转向系和电机模型

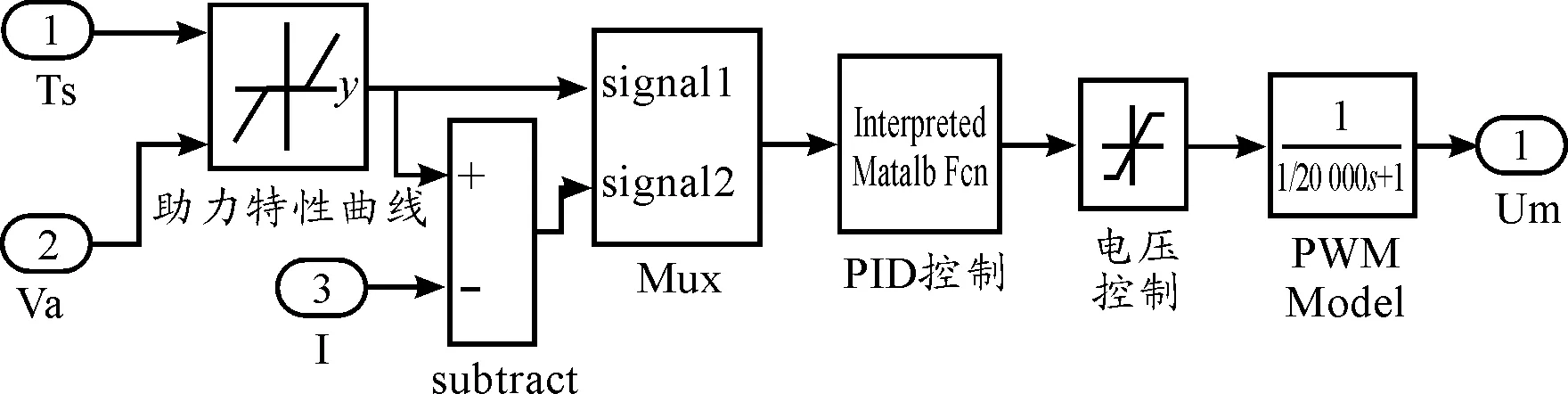
图9 控制器模型

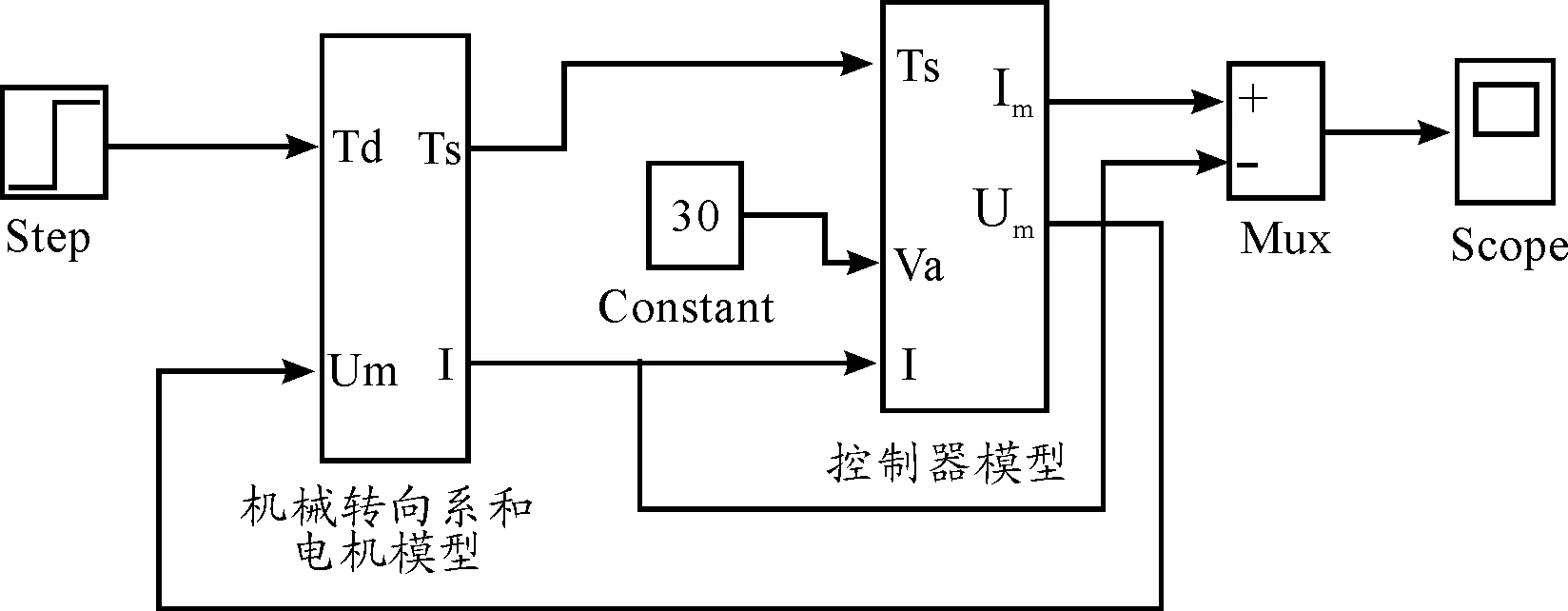
图10 PID控制模型

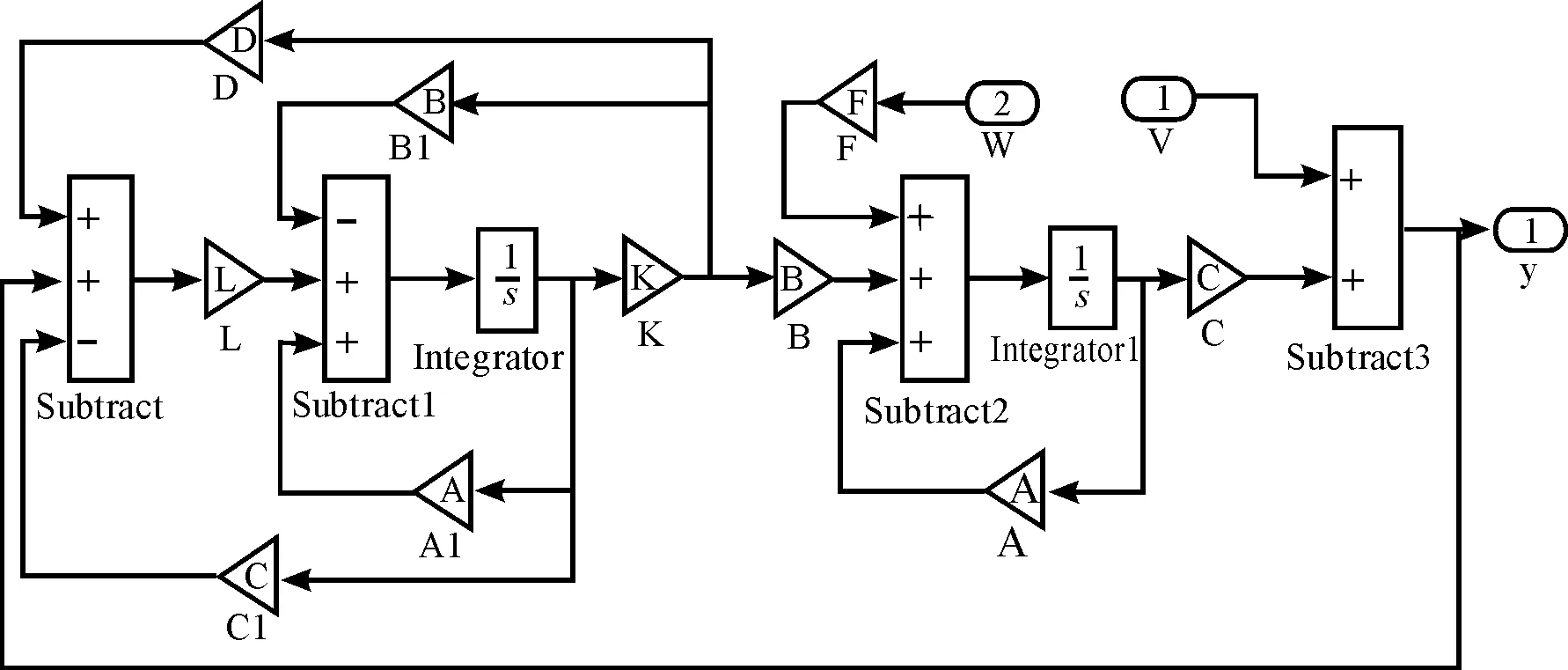
图11 LQG最优控制模型

3.2 仿真分析

应用Matlab7.1中的控制工具箱，分别采用PID控制和LQG-PID两种控制策略[8]对EPS系统进行仿真分析。仿真模型的主要参数见表1。

表1 仿真模型所用主要参数

设在路面随机噪声w(k)的方差输入值为0.135,测量噪声v(k)的方差输入值为0.079的干扰情况下,车速v取值为30 km/h,转向盘输入转矩为约35 N·m的阶跃信号，通过对电流误差加权系数q的不断仿真调试,最后当q取21时,系统的性能达到最佳[9]。 转向盘经过电机助力作用后所受到的转矩如图12所示。 由图中可以看出:LQG-PID控制与传统PID控制相比，转矩的响应波动相应较小,而且输出响应较平稳。图13是电机在两种控制策略下，车速为30 km/h时实际输出助力电流与目标助力电流的阶跃响应曲线。图14是车速为60 km/s时，电动机实际输出助力电流与目标助力电流的响应曲线。可以看出随车速的增加，助力电流减小，即电动机提供的助力减小，车辆行驶稳定性提高，且LQG-PID控制能使电动机的实际助力电流与目标电流之间的误差最小，即使EPS系统具有良好的抗干扰性。

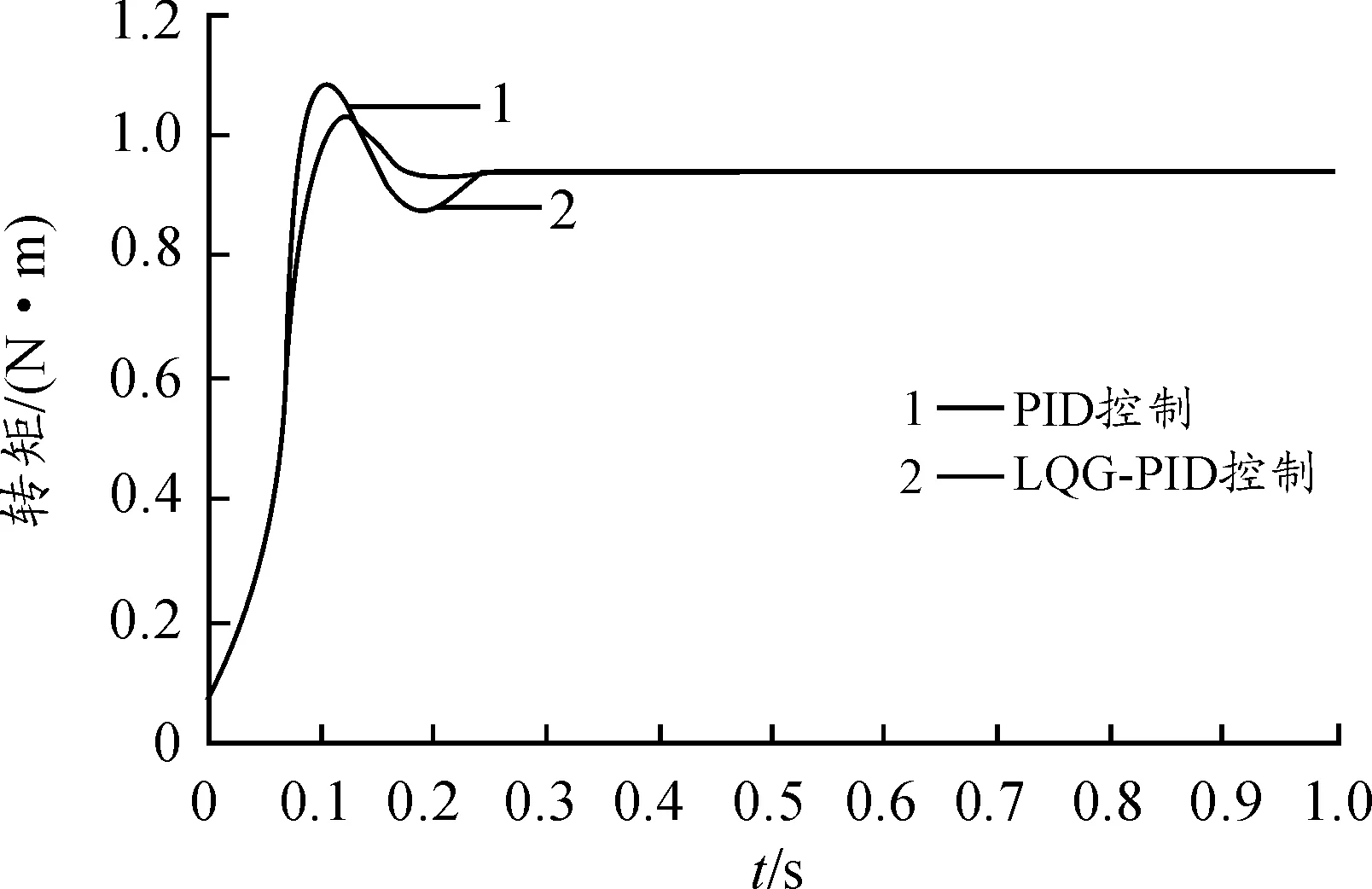
图12 转矩阶跃响应

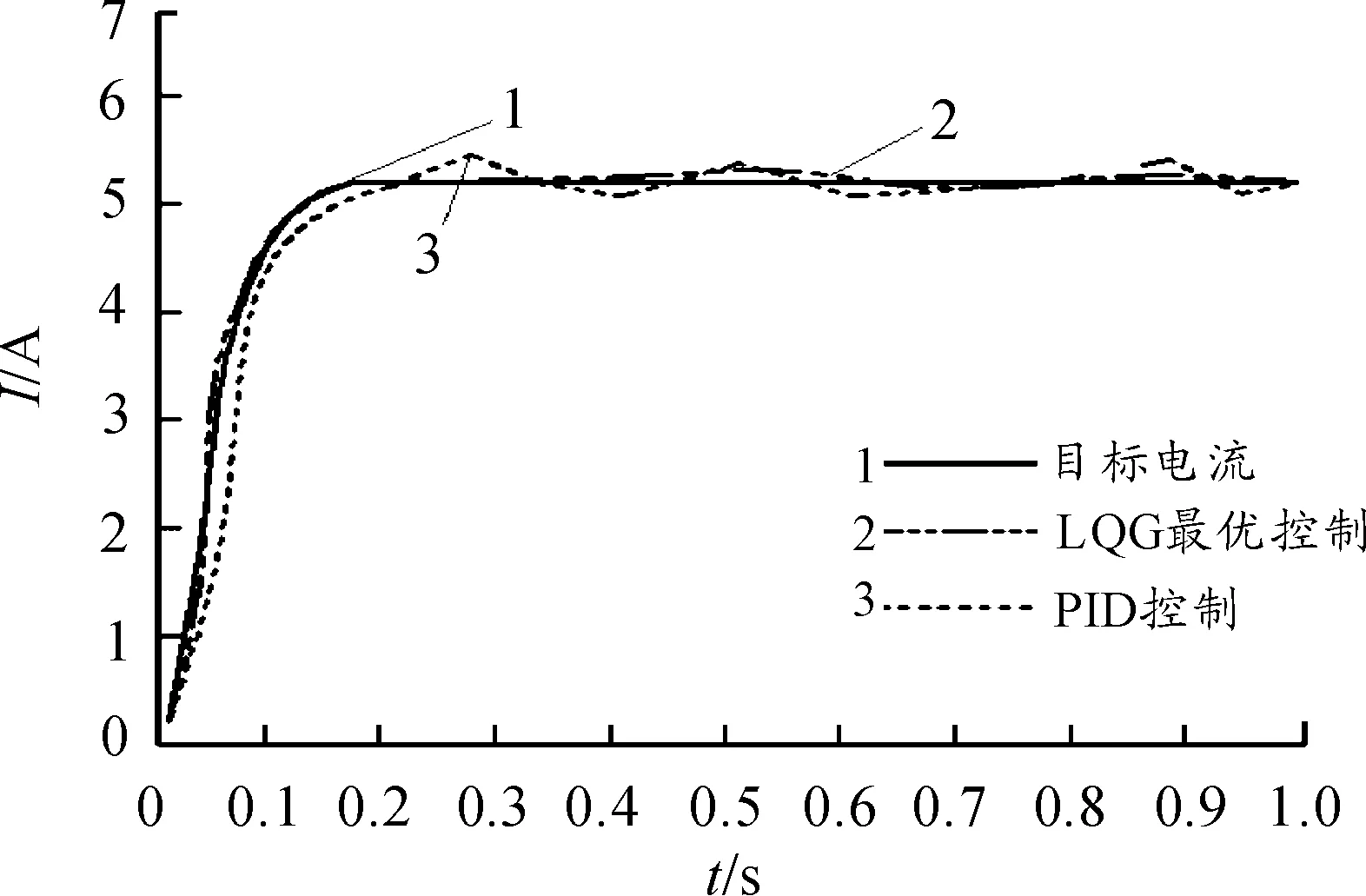
图13 车速为30 km/h时电机助力电流阶跃响应曲线

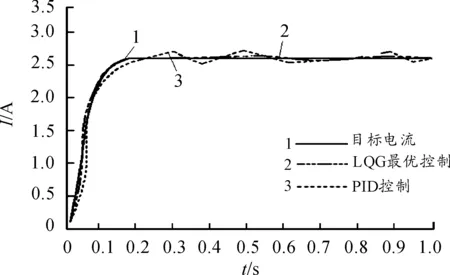
图14 车速为60 km/h时电机助力电流响应曲线

4 结束语

通过对EPS系统进行数学建模并进行仿真分析可见，本文设计的LQG-PID最优控制器使助力后转矩的输出响应波动较小且平稳，电动机的实际助力电流与目标电流之间的误差最小，即能有效降低系统本身的模型参数不确定性、路面随机激励以及转矩传感器测量噪声等因素的干扰，提高EPS系统的鲁棒性。

[1] 李伟，宋晓华.基于MSC1210单片机的汽车电动助力转向ECU系统的开发[J].客车技术与研究，2012(1)：8-10.

[2] 夏天,陈龙,黄晨,等. EPS模糊滑模变结构控制仿真及试验研究[J].重庆理工大学学报：自然科学版，2014(3)：17-21.

[3] 卢娟.电动助力转向系统建模与仿真研究[D].重庆：重庆大学，2006.

[4] 田正新.汽车电动助力转向控制策略的研究及联合仿真分析[D].长沙：湖南大学，2012：37-39.

[5] 高士香.汽车电动助力转向系统LQG最优控制研究[D].淄博：山东理工大学，2009.

[6] Li Ke.Robust control for electric power steering system[D].Canada:University of Windsor,2004.

[7] Chen Xiang,Chen Xiaoqun,Li Ke.Robust control of electric power-assisted steeringsystem[M].USA：IEEE,2005:101-105.

[8] 陈无畏，王妍.汽车电动助力转向系统的自适应LQG控制[J].机械工程学报，2005,41(12):27-30.

[9] 巨永锋,李登峰.最优控制[M].重庆:重庆大学出版社,2005.

(责任编辑 刘 舸)

Based on LQG-PID Optimal Control of EPS System

SHAO Xian-you, LI Zhi-peng, YANG Chuan-ying, LI Xiao-ying

(Traffic College, Northeast Forestry University, Harbin 150040,China)

Due to the system itself uncertainty of model parameters, road random excitation and torque sensor measurement noise and other factors interference, using traditional PID control methods cannot meet the precise control of the Electric Power Steering (EPS) system. By building a mathematical model of the EPS system and adding random noise signal, we created a system of state space expression and designed linear quadratic Gaussian on the basis of PID control (LQG) state feedback controller that was optimized LQG-PID control. With minimum energy consumption as objective function, using Matlab/Simulink simulation analysis of EPS system, the resulting simulation curves show: application of LQG-PID control method can effectively reduce the system subject to random disturbances, the error of the actual energy consumption and electric motor assist current and target current minimum, which improves the robustness of the EPS system.

electric power steering system; PID control; LQG-PID controller; optimal control

2015-05-28 基金项目：黑龙江省自然科学基金资助项目(E050301)

邵宪友(1990—)，男，黑龙江五大连池人，硕士研究生，主要从事汽车电子控制技术研究；李志鹏(1963—)，男，黑龙江哈尔滨人，博士，教授。主要从事汽车电子控制技术研究。

邵宪友,李志鹏,杨传英，等.基于LQG-PID的EPS系统最优控制[J].重庆理工大学学报：自然科学版，2015(9):42-47.

format：SHAO Xian-you, LI Zhi-peng, YANG Chuan-ying, et al.Based on LQG-PID Optimal Control of EPS System[J].Journal of Chongqing University of Technology:Natural Science，2015(9):42-47.

10.3969/j.issn.1674-8425(z).2015.09.007

TM572

A

1674-8425(2015)09-0042-06