函数性线性回归模型分析方法及其应用

刘 锋，谭祥勇，何 卓

(重庆理工大学数学与统计学院，重庆 400054)

函数性线性回归模型分析方法及其应用

刘 锋，谭祥勇，何 卓

(重庆理工大学数学与统计学院，重庆 400054)

研究了自变量为函数性数据、响应变量为标量的函数性线性模型在Tecator Data数据集上的应用。分别利用低阶基函数的线性组合、带粗糙惩罚的高阶基函数的线性组合以及函数性主成分分析法得到函数性线性模型中回归函数的估计。结果表明:这3种方法都能较好地估计出回归函数，而其中函数性主成分分析法表现最优。

函数性数据分析;函数性线性模型;函数性主成分分析

在传统的数据分析中，通常所遇到的数据要么是截面数据，要么是时间序列数据。这些数据离散且具有有限的特征，并且有诸多的不足之处。例如，纵向数据过分依赖于条件假设，并且样本所观测到的数据都处于同一时间点。对于那些在不同时间上所观测的数据，传统的方法就不能很好地进行统计推断。随着科学的进步，我们所收集的数据不但包括一般的离散型数据，还包括具有函数形式的过程所产生的数据，例如数据自动收集系统收集的数据等，一般称这种数据为函数性数据。函数性数据分析(functional data analysis)的概念最早由加拿大学者 Ramsay和 Dalzell于1991年提出，并且在文献［1］中使用函数性主成分分析和线性模型对加拿大的温度和降雨量进行了实证分析。虽然函数性数据来源形式多样，但其本质都是由函数构成。因此，在对函数性数据进行分析时，可将观测到的数据看作一个整体，而不是一串数字，这是函数性数据分析与传统的统计分析的主要区别。近年来，对函数性数据分析方法的研究己有不少的成果，比如线性回归分析［2-5］、函数性方差分析、函数性主成分分析、函数性典型相关分析、聚类分析［6］等。另外，利用拟合的光滑函数的导数对数据分析也取得了不少成果。张莹等［7］介绍了主微分分析方法的原理。剡亮亮［8］介绍了主微分分析方法在函数性数据中的应用。

本文运用3种不同的方法来研究自变量是函数、因变量为标量的函数性线性模型在 Tecator Data数据集上的应用，通过实证分析来展现函数性数据的一些优势和特征。

1 函数性线性回归模型与估计方法

函数性线性模型可分为协变量为函数性数据、响应变量为标量，协变量为标量、响应变量为函数性数据和协变量、响应变量均为函数性数据这3种情况。对于第1种情况，其模型为

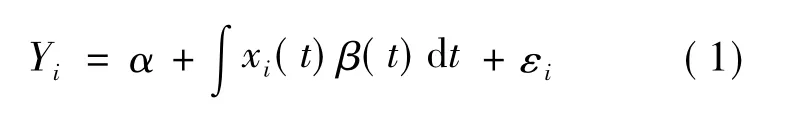
其中β(·)为未知的回归函数。为得到其估计，设一组基函数为φk(t)，k=1，2，…，K，然后用低阶的基函数的线性组合、带粗糙惩罚的高阶基函数线性组合以及函数性主成分分析法得到回归函数的估计。本文主要利用这3种方法来进行建模。

2 建立函数性线性模型

2.1 数据来源

本文数据来源于R软件中的fda.usc程序包中的tecator data的数据。该数据集包含了240个样本，每个样本由100道吸收谱以及水分、脂肪、蛋白质各占的比例所组成，其中前172个样本为训练集，后68为测试集。为此，本文主要研究光谱的吸收率与水分的比例关系，且只取前172个样本。

2.2 函数性线性模型建模

本文以光谱吸收率作为自变量x，以每个样本所含水分的比例作为响应变量Y，则所建立的函数性线性模型为(1．1)。由于得到的自变量是离散的，因此首先要将离散的数据转化为函数形式，即利用所观测的原始数据定义一个函数x(t)。如果获得的离散值没有观测误差，就称这个过程为插值;如果获得的数据含有观测误差，那么在将离散数据转化为函数时，就需要对数据进行修匀。解决这个问题的方法就是先选定一组基函数，然后利用基函数的线性组合来给出x(t)的估计。一般情况下，选择B-样条基和傅里叶基。前者适用于非周期性函数性数据，后者适用于周期性函数性数据。本文选取B-样条基来拟合样本。图1为172个样本的修匀曲线。

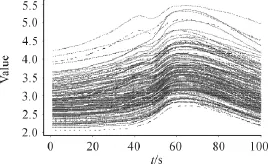
图1 172个样本的修匀曲线

以下将分别利用本文提到的3种方法来估计回归函数。

1)采用低阶基函数的线性组合估计回归函数，即

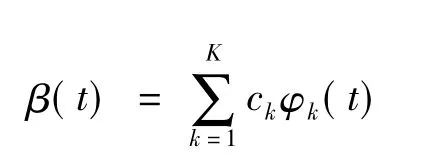
在此方法中，设K=21。通过R软件的计算，得到了截距α的估计为0．007 2，回归参数函数β(t)的拟合曲线如图2所示，其中虚线是置信度为95%的置信区间。通过计算，可以得到R2= 0.963 2，F=177．347 7，其中:R2为判定系数，反映模型的拟合优度;F值反映方程的显著性。图3显示了真实值与预测值，其中○表示真实值，△表示预测值。从图3可以看出:函数性线性模型具有较好的预测功能。

图2 利用低阶基函数的线性组合估计的回归函数拟合

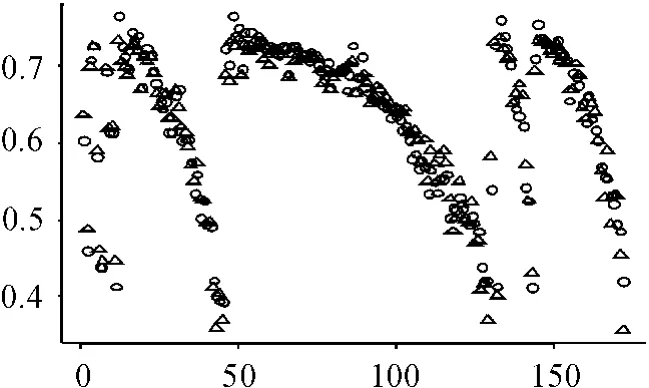
图3 真实值与预测值

2)利用带粗糙惩罚的高阶基函数的线性组合来估计回归函数。

为了得到β(t)的估计，由文献［9］可以极小化式(2)。

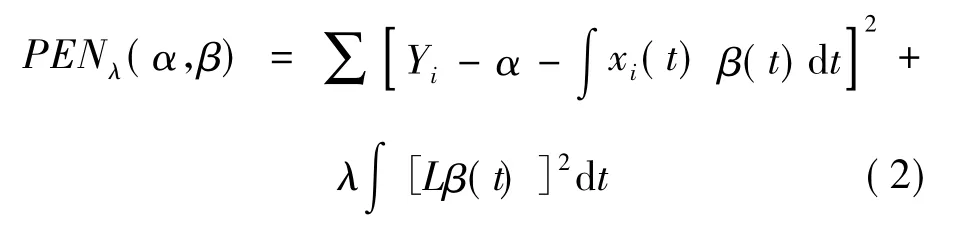
从式(2)可以看出:惩罚系数λ决定着β(t)的光滑程度，为此采用交叉核实方法来选择光滑系数。由图4可见:建议选择光滑系数λ=10-5。

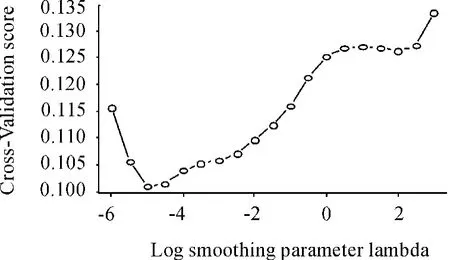
图4 光滑参数估计效果

在此方法中，设K=63。通过R软件的计算，得到了截距α的估计为0．007 2，回归参数函数β(t)的拟合曲线如图5所示，其中虚线是置信度为95%的置信区间。通过计算，可以得到R2= 0.970 6，F=165．449 2。图6展示了其残差的QQ图，说明用高阶基的线性组合，并加上粗糙惩罚所估计的方程和回归函数都是有效的。

图5 带粗糙惩罚的回归参数拟合

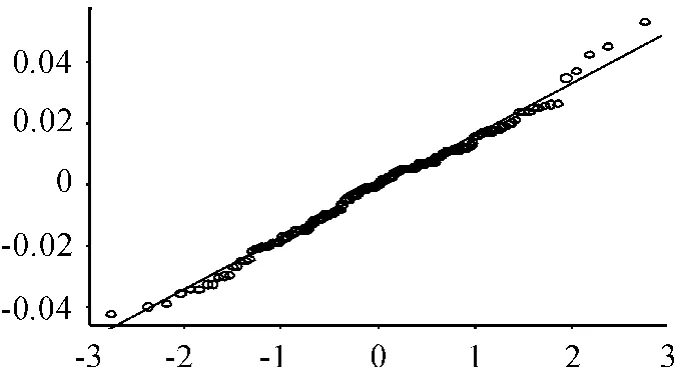
图6 残差的QQ图

3)利用函数性主成分分析方法来估计回归函数。

在离散型数据分析中，为了处理高维数据，往往会利用主成分分析来进行降维。同样，在函数性数据分析中，也可以利用函数性主成分分析法来提取样本的主要成分。

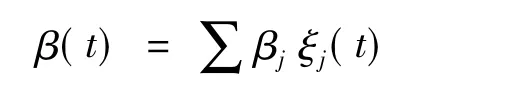
为此先进行主成分分析。本文选取了前4个主成分。图7展示了前4个主成分偏离均值的效果。

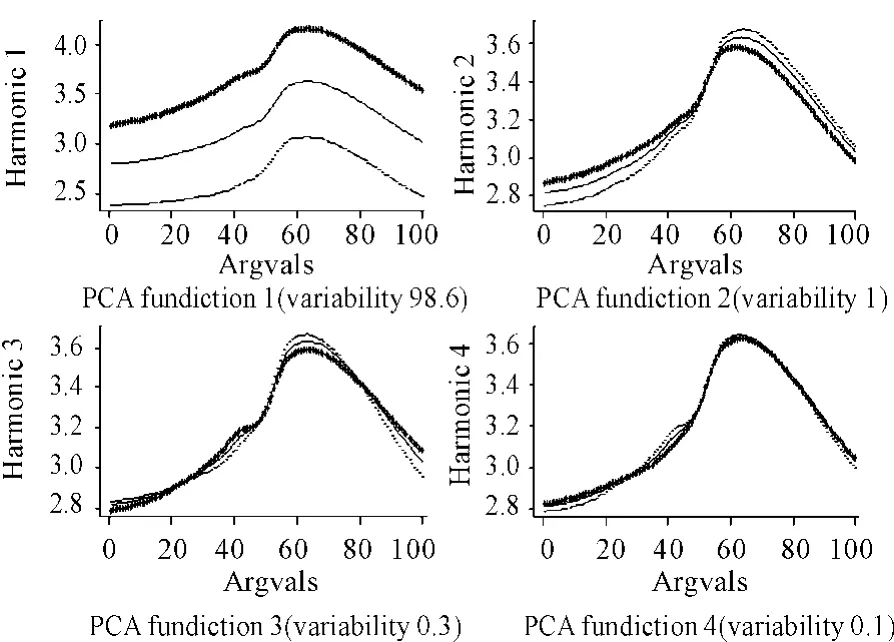
图7 前4个主成分偏离均值的效果

通过计算，β0的估计为0．632 2。图8给出了β(t)的估计和其估计的逐点置信区间，其中虚线是置信度为95%的置信区间。从图8和图9可以看出:主成分分析方法同样有较好的效果。

图8 利用函数性主成分分析方法所估计的回归参数拟合

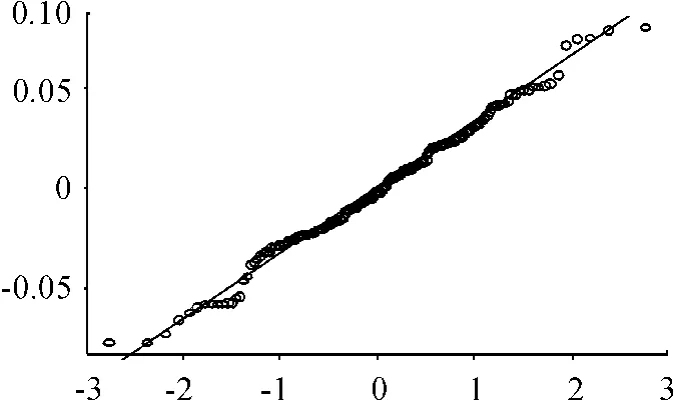
图9 残差的QQ图

3 结束语

本文通过低阶基函数的线性组合、带粗糙惩罚的高阶基函数线性组合和函数性主成分分析法来估计函数性线性模型的回归函数。结果表明:这3种方法对数据都有较好的解释能力。另外，从回归函数的置信区间上看，利用主成分分析方法得到的估计比其他2种方法好。这与普通的线性模型所表现的结果相同。与传统的多元数据分析相比，函数性数据分析具有较多的优越性。比如:函数性数据分析只依赖较少的假设条件和较弱的收敛结构等;函数性线性模型可以处理高维的数据，而传统的线性模型遇到高维的数据就显得无能为力。

［1］Ramsay J O，Dalzell C J.Some tools for functional data analysis［J］.Journal of the Royal Statistical Society，1991，Series B:539-572.

［2］Cardot H，Ferraty F，Sarda P.Functional linear model［J］.Statistic&Probability Letters，1999，45(1):11-22.

［3］Cardot H，Ferraty F，Sarda P.Spline estimators for the functional linear model［J］.Statistica Sinica，2003，13 (3):571-592.

［4］He G，Müller H G，Wang J，et al.Function all inear regression via canonical analysis［J］.Bernoulli，2010，16 (13):705-729.

［5］Yao F，Müller H G，Wang J L.Functional linear regression analysis for longitudinal data［J］.The Annals of Statistics，2005，33(6):2873-2903.

［6］曾玉钰，翁金钟.函数数据聚类分析方法探析［J］.统计与信息论坛，2007，22(5):10-14.

［7］剡亮量.基于函数性视角的经济数据分析—以主微分分析为例［J］.统计与信息论坛，2013，28(1):40-46.

［8］张莹，叶振军.主微分分析方法在金融工程研究中的应用［J］.统计与决策，2009(9):41-31.

［9］James O R，Hooker G，Graves S.Functional Data Analysis with R and MATLAB［M］.［S.l.］:Springer，2009.

(责任编辑刘 舸)

Methods of Functional Linear Regression Model and Its Applications

LIU Feng，TAN Xiang-yong，HE Zhuo
(College of Mathematics and Statistics，Chongqing University of Technology，Chongqing 400054，China)

We investigated the application of functional linear model in Tecator Data set with a scalar response and functional covariates.Then，we used the low-dimensional basis，combination of a highdimensional basis with a roughness penalty and low-dimensional approximation using principal component analysis method to estimate the regression function.The result show that these three methods perform can perform well in estimating regression function，especially the last method.

functional data analysis;functional linear model;functional principal analysis

O21

A

1674-8425(2015)11-0135-04

10.3969/j.issn.1674-8425(z).2015.11.023

2015-07-21

国家自然科学基金资助项目(11471060)

刘锋(1973—)，男，湖北新化人，博士，副教授，主要从事非参数统计研究。

刘锋，谭祥勇，何卓.函数性线性回归模型分析方法及其应用［J］.重庆理工大学学报:自然科学版，2015 (11):135-138.

format:LIU Feng，TAN Xiang-yong，HE Zhuo.Methods of Functional Linear Regression Model and Its Applications［J］.Journal of Chongqing University of Technology:Natural Science，2015(11):135-138.