不对称均值回复及相关技术交易策略研究

刘婷婷

(天津大学管理与经济学部，天津 300072)

不对称均值回复及相关技术交易策略研究

刘婷婷

(天津大学管理与经济学部，天津 300072)

资产收益和波动之间的关系一直以来都是金融经济学中的研究重点。通过研究股票收益不对称回复特性，提出了新的技术交易策略。以上证综合指数为例检验日收益动态性中的不对称性，结果得出:买入信号产生一个正收益，卖出信号产生一个负收益，对买卖信号差产生正收益。

不对称;均值回复;交易策略

各种研究说明技术交易策略具有赢利能力，它试图找到过去价格中存在的规律，从而对其未来走势作出预测。这些策略在权益市场的有效性依赖于“市场价格盈利模型在未来会持续”的假设。因此，技术分析必须能够基于可识别的模式预测市场价格的运动。

外国学者Brock［1］说明了基于短期和长期移动平均运动的简单技术交易规则具有预测能力。他以一个世纪的纳斯达克工业指数平均日数据为样本，发现买入信号总产生正收益，而卖出信号会带来负收益。基于此证明，一些学者也提出关于收益产生过程的参数模型并不能充分解释技术交易策略的获利能力。

根据早期技术分析多利用移动平均规则，买卖信号是由一个短期和一个长期移动平均之间的关系产生的。短期移动平均在长期移动平均之上(下)产生买(卖)信号。这种基本策略有很多变化，如在移动平均附近引入带宽，或改变短期和长期的长度。如果股票价格运动到一个阻力(支撑)水平之上(之下)，交易触发原则就会刺激买入(卖出)信号。

于是学者们对移动平均规则进行了大量的研究，并在股票、期货和外汇市场等金融市场进行了实证检验，证明了该交易规则的有效性［2］。在这种背景下，一些基于神经网络的模型检验了技术交易规则的盈利能力。例如，Gencay［3］和Fernandez-Rodriguez［4］使用神经网络模型确定买、卖信号，并显示该技术交易规则总是优于单纯的买入持有策略。Genay and Stengos［5-6］使用前馈网络和最近邻居回归，发现简单的技术交易规则具有对预测收益显著的预测能力。

与此同时，Gencay［7］和 Gencay and Stengos (1997)也发现了买卖信号在预测道琼斯工业指数平均日收益上的非线性预测能力。大多数关于技术交易规则盈利能力的bootstrap检验假设回复过程是一个线性的动态关系，而这种假设不能获得盈利。因此，一些研究建议回报产生过程用非线性模型表征，而且利用非线性模型的技术交易规则可能获得收益。随后，学者们对动态回报的非线性随机过程产生了兴趣。一些最近的研究表明:股票市场回报的可预期部分是随机和非线性的，且可用一个不对称的动态过程来解释。Kiseok Nam等［8］使用S&P500指数的日收益数据，检验了股票收益的波动不对称性，探索了股票收益不对称的动态过程与技术交易策略如何盈利的关系。

国内研究者对技术交易研究较少［9］，其中邓杰、唐国兴［10］验证了移动平均线和阻力线-支撑线交易规则在上证综指上的有效性。于是，对中国股票市场的不对称回复模式进行观察，以期提出创新交易策略，并在上证综合指数上检验其盈利性。

1 不对称回复模式

本文对上证综合指数的日收益的最初检验显示出收益动态性的不对称模式。正收益比负收益持续时间更长［11］。表1显示不对称的初步结果是:连续观察2，3，4，5天正的和负的收益序列。同样，对2，3，4，5天持有期，每种情况正收益区间的数量大于负收益区间的数量。对01/04/93-05/28/10整个区间上的日收益，有91个5交易日连续上涨，相对于86个5交易日连续下跌;212个4交易日连续上涨对186个4交易日连续下跌; 460个3交易日连续上涨对415个3交易日连续下跌;1 044个2交易日连续上涨对963个2交易日连续下跌，如表1所示。

表1 不同收益模式下各种情景的数量

2 模型机研究方法

以股票动态收益的不对称性和技术较策略的关系为重点，采用Kiseok Nam(2005)的非线性自回归模型，股票收益的自回归过程Rt为:

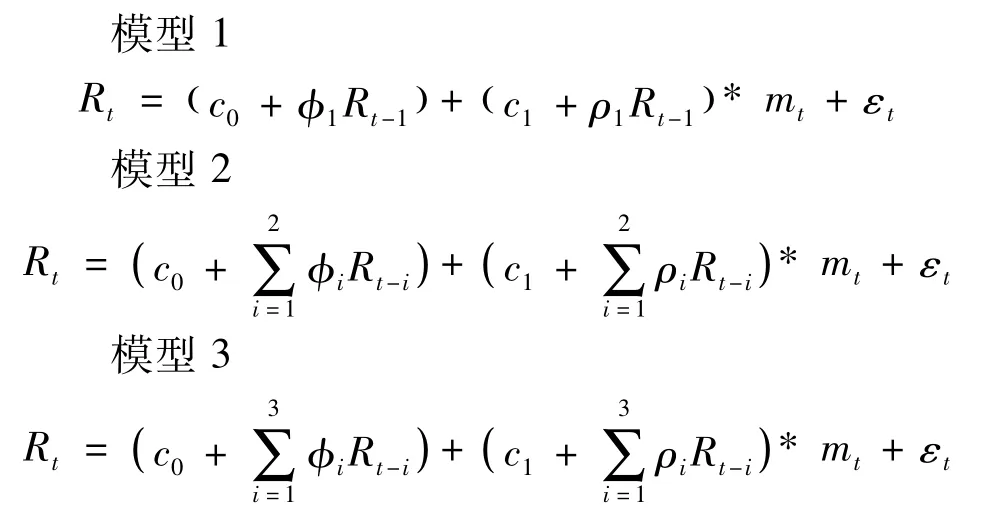
每个模型代表一个非线性AR(m)模型，对m=1，…，5，允许常数项和序列相关系数随着前面正或负的收益模式的变化而变化。对应这5个模型，定义了4种不同的前期收益模式情景:PH-m情景(NH-m情景)代表前m交易日为正(负)的持有期收益的不对称模式。PC-m情景(NC-m情景)代表前m交易日连续正(负)收益下的不对称模式。

在每个情景下对5个模型做出估计，满足mt=1的条件决定了相应的需要估计的模型。例如，PH-3代表之前3天的一个持有期回报，当此收益(Rt-1-Rt-2-Rt-3)为正时，取mt=1。在PH-3的情况下，被估计的模型将是模型3。对每种情景，收益序列相关性在mt=1条件下由度量，在mt=0时则为个模型度量条件相同。例如，在PH-3的情况下，当3天的持有期收益为正时，回报序列的相关性用φ1+ φ2+φ3+ρ1+ρ2+ρ3来衡量，否则用φ1+φ2+φ3来衡量;收益动态性的不对称性由识别。这表明了收益估计过程具有额外的预测能力。各模型的自相关系数之和显示了使用前期收益模式的收益动态性的持续性或反转信息。

一旦识别了mt=0和1的收益序列的自回归过程，就可以计算自回归过程所隐含的无条件均值。各模型下Rt的隐含无条件均值，对mt=0为对mt=1为(c0+c1)/［1-可预测性由自回归系数度量，而盈利能力通过无条件均值进行分析。

3 实证

3.1 数据描述

使用01/04/93到05/28/10间的上证综指的日收益序列进行估值。表2列出了指数在整个区间日名义收益的描述性统计量。可以看到:日收益显示出过度的峰度，并且在整个区间有显著的自回归过程。所有自相关系数均在1%水平上统计显著，且自相关系数的和为正。但常数自相关系数没有描述收益过程的不对称特征，如表1所示。

3.2 估值结果和解释

表3显示了模型1～5在整个区间上的估值结果。日收益显示出很强的不对称。正收益比负收益持续时间更长。该不对称如果在5个模型中都出现，应该在 PH-m情景和 PC-m情景下由和识别，而在NH-m情景和NC-m情景下由识别。

表格A显示PH-m情景和NH-m情景下模型1～5的估计结果，其中不对称性是由前m个交易日持有期收益模式定义的。因此，PH-m情景下，前m交易日持有期收益为正时，m=1;NH-m情景下，前m交易日持有期收益为负时m=1。ψ0为不对称自相关系数之和，增强了预测能力。F-STAT代表零假设为ψ0=0的F统计，所有的F统计在1%水平上统计显著，模型4在5%水平上显著。因此，这5个非线性自回归模型对以前期正和负的持有期收益的收益模式中不对称回复部分有很强的解释能力。

表2 上证综合指数日收益的统计量

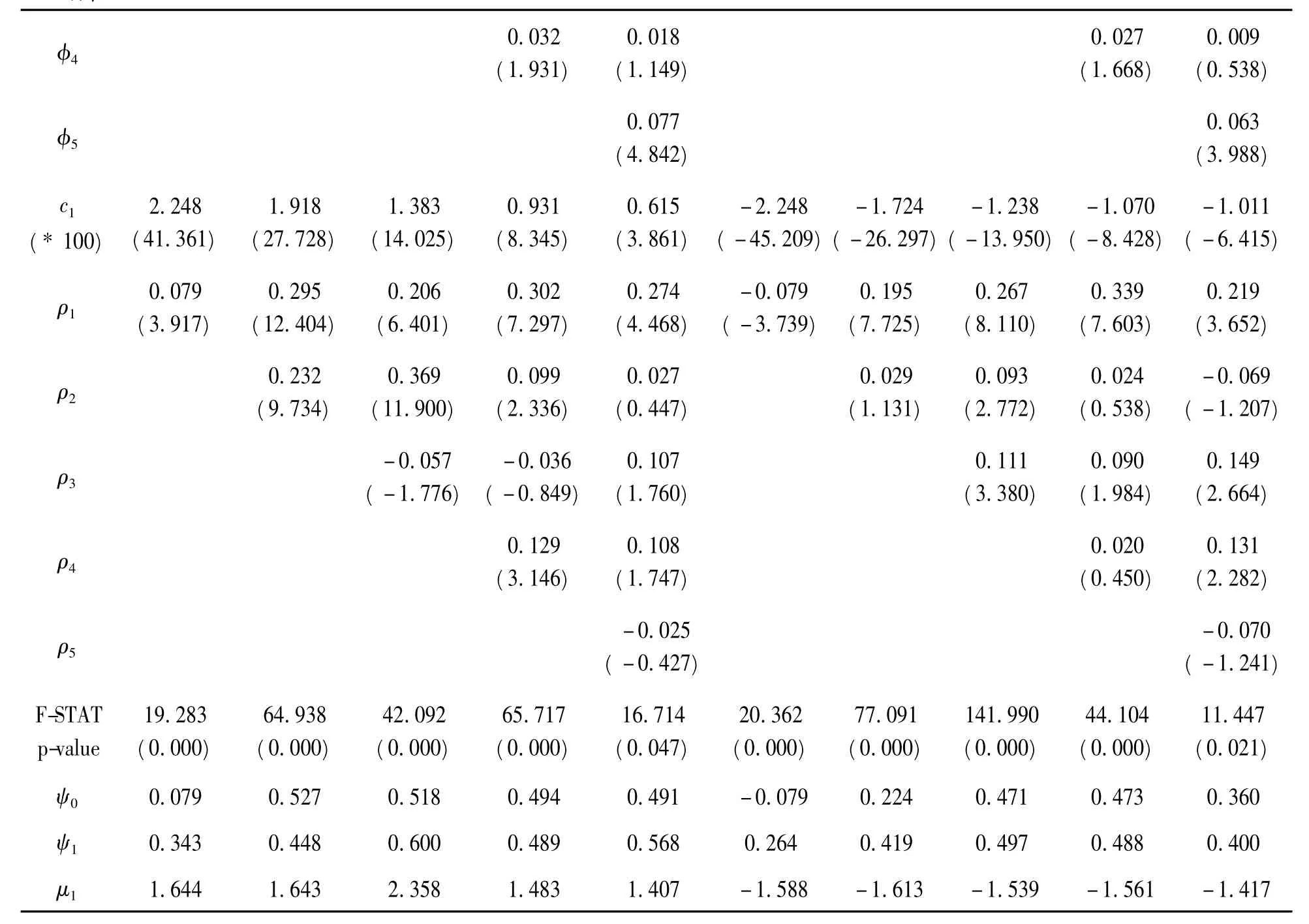
φ4 0．032 (1．931) 0．018 (1．149) 0．027 (1．668) 0．009 (0．538)φ5 0．077 (4．842) 0．063 (3．988)c1 (*100) 2．248 (41．361) 1．918 (27．728) 1．383 (14．025) 0．931 (8．345) 0．615 (3．861) -2．248 (-45．209) -1．724 (-26．297) -1．238 (-13．950) -1．070 (-8．428) -1．011 (-6．415)ρ1 0．079 (3．917) 0．295 (12．404) 0．206 (6．401) 0．302 (7．297) 0．274 (4．468) -0．079 (-3．739) 0．195 (7．725) 0．267 (8．110) 0．339 (7．603) 0．219 (3．652)ρ2 0．232 (9．734) 0．369 (11．900) 0．099 (2．336) 0．027 (0．447) 0．029 (1．131) 0．093 (2．772) 0．024 (0．538) -0．069 (-1．207)ρ3 -0．057 (-1．776) -0．036 (-0．849) 0．107 (1．760) 0．111 (3．380) 0．090 (1．984) 0．149 (2．664)ρ4 0．129 (3．146) 0．108 (1．747) 0．020 (0．450) 0．131 (2．282) -0．070 (-1．241) F-STAT p-valueρ5 -0．025 (-0．427) 11．447 (0．021)ψ0 0．079 0．527 0．518 0．494 0．491 -0．079 0．224 0．471 0．473 0．360ψ1 0．343 0．448 0．600 0．489 0．568 0．264 0．419 0．497 0．488 0．400μ1 1．644 1．643 2．358 1．483 1．407 -1．588 -1．613 -1．539 -1．561 -1．417 19．283 (0．000) 64．938 (0．000) 42．092 (0．000) 65．717 (0．000) 16．714 (0．047) 20．362 (0．000) 77．091 (0．000) 141．990 (0．000) 44．104 (0．000)

ψ0为不对称自相关系数之和;F-STAT代表ψ0=0的零假设。ψ1为m=1自相关系数之和，计算代表m=1的无条件均值，计算为μ1=(c0+c1)/(1-ψ1)。

ψ1度量mt=1下每个模型的自相关系数之和，例如因此，对于PH-m情景，ψ1度量正的前m交易日持有期收益下的收益序列相关性。对NH-m情景，ψ1度量负的前m交易日持有期收益下的收益序列相关性。结果显示:除模型1相关性为正，指数收益在前m交易日持有期收益为正时，显示出负的序列相关性;在前m交易日持有期收益为负时，除模型1和2，其余3个模型的相关性为负。并未如Kiseok Nam(2005)的证明:显示出正负收益的持续性，在正收益之后很可能为负，而负收益之后很可能为正。

μ1(=(c0+c1)/(1-ψ1))代表mt=1时收益的无条件均值。结果显示:对μ1＞0的PH-m情景，前期持有期收益为正时，无条件均值为正;对μ1＜0的NH-m情景，前期持有期收益为负时，无条件均值为负。

表3中的B列显示模型1～5在PC-m和NC-m情景下的估计结果，其中不对称定义为前m个连续交易日日收益为正或负。PC-m情景下，当前m个连续交易日日收益为正时，mt取值为1;而在NC-m情景下，当前m连续交易日日收益为负，mt取值为1。检验ψ0=0的零假设的F统计，在除了模型5在5%的水平上显著的所有情景下都在1%的水平上显著。在PC-m情景下，ψ0和ψ1证明了前面所描述的ψ0＞0和ψ1＞0(正收益的持续性);然而在NC-m情景下的结果并非ψ0＜0和ψ1＜0，此模型没有显示收益持续性。

3.3 研究结论

1)日收益显示出强不对称性，正收益持续时间比负收益长。

2)不对称非线性自回归模型得到的收益的无条件均值，不具备Kiseok Nam(2005)描述的持续性，在正的无条件均值之后很有可能出现负的无条件均值，而负的无条件均值之后则可能为正的无条件均值。

这为交易策略的盈利能力提供了有力证明。结果说明:在近期负向价格变动之后持有多头头寸很可能比近期正向价格变动之后持有空头头寸获得更大的包含交易成本的收益。该发现与表6中的结果一致，对买入信号产生正收益，对卖出信号产生负收益。

4 交易策略和盈利分析

本文利用收益动态性的不对称回复模式来生成盈利性交易策略。确认买入和卖出信号的交易规则由前m交易日持有期收益和前m个连续交易日收益模式控制。在前持有期收益模式下，NH-m情景产生买入信号，PH-m情景生成卖出信号。同样，在前连续收益模式下，NC-m产生买入信号，PC-m情景产生卖出信号。每种规则有5种交易策略可以执行，对应不同的参数m。在前期持有期收益规则下，当前2个交易日持有期收益为负，m=2策略最初产生一个买入信号;当前2个交易日持有期收益为正，则为卖出信号。在前期连续收益规则下，当前2个连续交易日收益为负(正)，策略m=2初始化一个卖入(买出)信号。m=1策略在2种规则下的初始值是相同的。

表4列出了2种交易规则下，使用上证综合指数日收益数据的交易策略的标检测试结果。Column 1代表每种规则下由m值定义的不同策略。第2、3列代表不同策略买入和卖出信号数量;第4、5列显示买入和卖出期间的平均日收益，用相应的t统计检验无条件单日收益均值与买入均值和卖出均值之间是否存在差异;第6、7列显示买入和卖出收益大于零的比例;最后一列显示买卖价差，为平均日买入收益减去平均日卖出收益。

当买入信号都产生显著的正收益，卖出期间收益显著为负，且买入和卖出信号价差为正，则策略成功。表4中的结果显示:买入信号通常生成统计上显著的正收益，卖出信号产生负收益。对前持有期收益模式下的策略，买入收益都为正，平均日收益为0.664 7%(年172.822%)。该结果与无条件日收益均值0.060 1%(年15.63%)相比。卖出收益为负，平均日收益-0.568%(年-147.68%)。5种策略下的t检验推翻了买入和卖出收益与无条件日平均收益在1%置信水平上使用双侧检验，没有显著的不同的零假设。买卖收益价差在所有的策略中都为正，并在1%水平上统计显著，平均日价差为1.232 4%。同样，64.6%的买入信号产生正收益，64.0%的卖出信号产生负收益。

在前连续交易日收益模式下的策略中，前4个模型的策略在1%水平上统计显著。对这4种策略，表格显示正的买入信号，负的卖出信号，以及正的买卖价差。前连续收益模式的成功一部分源自下面的发现，即前m交易日持有期收益作为控制变量比，前m交易日连续收益模式的正或负模式能更好地识别不对称回复模式。

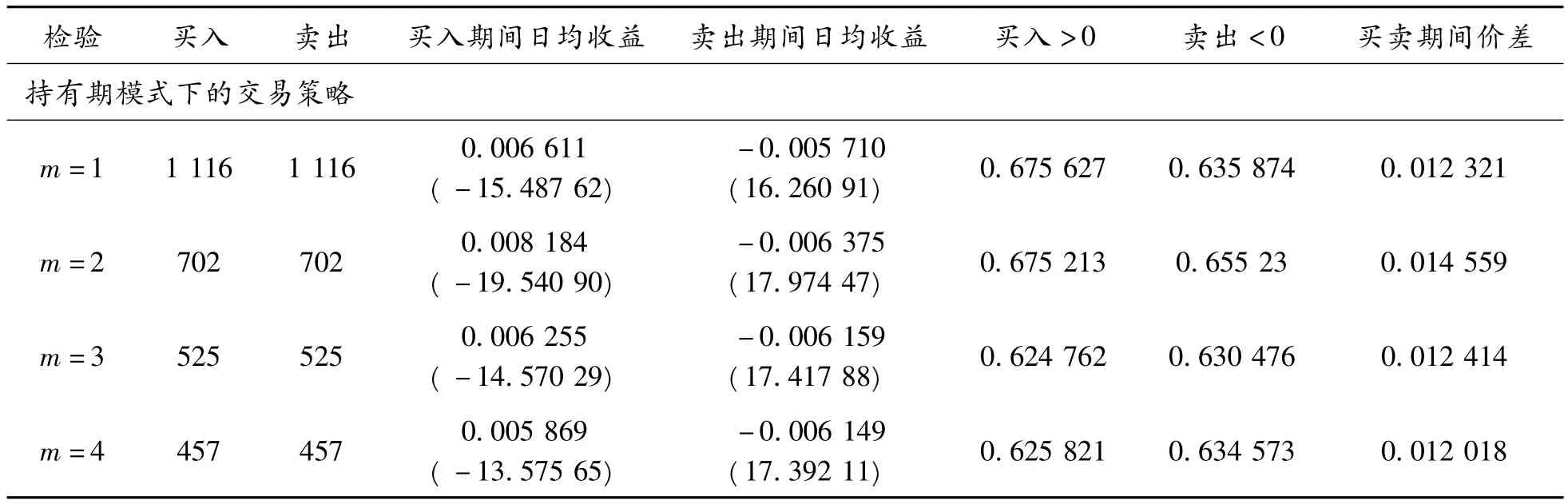
表4 交易策略检验结果

5 结束语

本文对上证综指采用不对称回复模式进行标准检验，说明技术交易策略的赢利性。首先，标准检验显示大多数策略对买入信号产生正收益，对卖出信号产生负收益，正的价差。买入(卖出)信号正(负)收益的来源是正(负)收益动态性的无条件均值，是由前期收益模式中识别的收益过程中的不对称发展而来，且基于前期持有期收益的策略产生比前期连续日收益模式控制的规则更可靠和一致的标准检验结果。这说明前期持有期收益模式能更好地识别该不对称，收益动态性中观察到的不对称可以产生盈利。

［1］Brock W J.Lakonishok，B Lebaron.Simple technical trading rules and the stochastic properties of stock returns［J］.Journal of Finance，1992，47:1731-1764.

［2］陈静，黄光辉.基于融资融券业务的新投资策略及应用［J］.重庆理工大学学报:自然科学版，2013，27(4): 116-121.

［3］Gençay R.Optimization of technical trading strategies and the profitability in security markets［J］.Economics Letters，1998(59):249-254.

［4］Femandez Rodr guez F，C Gonzalez-Martel，S Sosvilla-Rivero.On the profitability of technical trading rules based on artificial reural networks:evidence from the Madrid stock market［J］.Economics Letters，2000(69): 89-94.

［5］Gençay R，Stengos T.Technical trading rules and the size of the risk premium in security returns［J］.Studies in Nonlinear Dynamics and Econometrics，1997(2):23 -34.

［6］Gençay R，Stengos T.Moving average rules，volume and predictability of security returns with feedforward networks［J］.Journal of Forecasting，1998(17):401-414.

［7］Gençay R.The predictability of security returns with simple technical trading rules［J］.Journal of Empirical Finance，1998(5):347-359

［8］Nam K，Kenneth M W，Quentin C C.Asymmetric return dynamics and technical trading strategies［J］.Journal of Banking&Finance，2005，29:391-418.

［9］徐剑刚，陈为人.股票报酬时间序列统计特性［J］.外国经济管理，1996(S):50-54.

［10］邓杰，唐国兴.中国股票市场技术交易规则有效性的实证研究［J］.华东经济管理，2009(5):135-140.

［11］Ito A.Profits on technical trading rules and time-varying expected returns:evidence from pacific-basin equity markets［J］.Pacific-Basin Finance Journal，1999(7):283 -330.

(责任编辑何杰玲)

Asymmetric Return Dynamics and Technical Trading Strategies

LIU Ting-ting
(College of Management and Economics，Tianjin University，Tianjin 300072，China)

Relationship between the asset returns and volatility has always been a research focus in the financial economics.We investigated asymmetric reverting property of stock returns and raised the profitability of technical trading strategies.We identified an asymmetry in return dynamics for daily returns on the Shanghai composite index.Return dynamics evolve along a positive(negative)unconditional mean after a prior positive(negative)return.The trading strategies based on this asymmetry generate a positive return for buying signals，a negative return for sell signals and a positive return for the spread between buy and sell signals.

asymmetric;mean reverting;trading strategies

O213

A

1674-8425(2015)11-0144-07

10.3969/j.issn.1674-8425(z).2015.011.025

2014-11-17

国家自然科学基金资助项目(71071109)

刘婷婷(1989—)，女，硕士研究生，主要从事金融工程、公司理财、管理信息系统、中小企业融资研究。

刘婷婷.不对称均值回复及相关技术交易策略研究［J］.重庆理工大学学报:自然科学版，2015(11):144 -150.

format:LIU Ting-ting.Asymmetric Return Dynamics and Technical Trading Strategies［J］.Journal of Chongqing U-niversity of Technology:Natural Science，2015(11):144-150.