二维Helmholtz方程的边界元法

于善玲，张耀明

(山东理工大学理学院，山东淄博 255049)

二维Helmholtz方程的边界元法

于善玲，张耀明

(山东理工大学理学院，山东淄博 255049)

在已有位势问题工作的基础上，建立求解二维Helmholtz方程边值问题的间接变量规则化边界积分方程，它不包含CPV强奇异积分和HFP超奇异积分的计算。数值算例表明:本文方法在低频率下可取得较好的精度和效率。

二维Helmholtz方程边值问题;间接变量边界积分方程;边界元法;奇异积分

Helmholtz方程在工程技术、电磁场理论、散射理论、力学等较多领域有着广泛的应用，研究其数值解不仅有广泛的实际意义，也有重要的理论价值。在Helmholtz方程的边界型方法的研究中，主要是基本解法和直接边界元法［1-7］。基本解法通过虚拟边界避免奇异积分的计算，然而虚拟边界的优化选择是一个棘手的问题［5-6，8］，通常靠研究者的经验或误差实验来完成。本文致力于二维Helmholtz问题的间接变量规则化边界元法研究。与直接法相比，间接法更简单、灵活和适用［8-10］。首先，基本场变量和其导数不直接关联;其次，间接法更容易改变边界积分方程的形式，以适合不同边界条件的边值问题;再者，基本场变量的梯度方程中不含有HFP积分。然而，二维Helmholtz问题的间接变量规则化边界积分方程至今尚未得到充分的研究。本文在作者已有位势问题工作［9-10］的基础上，建立二维Helmholtz问题的间接变量规则化边界积分方程。它无需处理HFP积分，与已有的直接变量边界元法相比，降低了处理问题的复杂性，改进了计算效率。

1 预备知识

本文假定Ω是R2中的一个有界区域，Ωc是其补域，Γ=∂Ω是它们的共同边界。t(x)，n(x)分别是区域Ω的边界Γ在x点处的单位切、外法向量。

1.1 Helmholtz边界值问题

二维Helmholtz方程的控制微分方程为

混合边界条件为

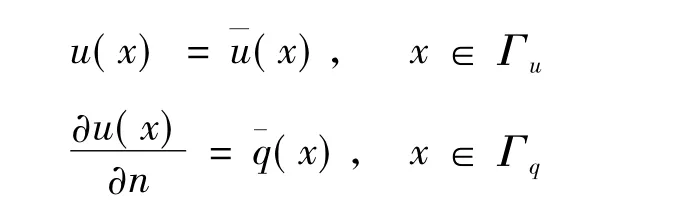
式中:u为势函数;分别是已知u和的边界。

二维Helmholtz方程的基本解为

定理1［9］设Γ是分段光滑曲线(开或闭)是Γ的一个点(可能是角点)，令若φ(x)∈C0，α(Γ)和是常数)，那么有

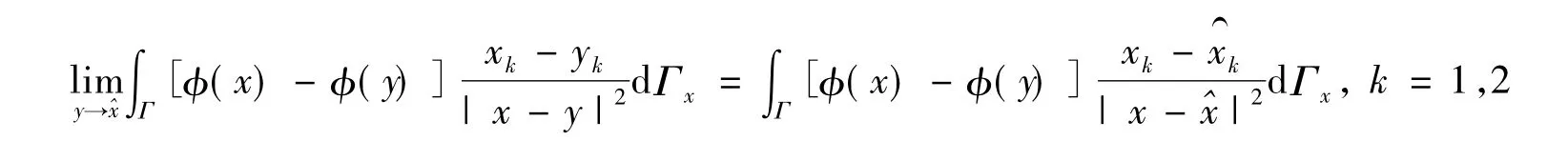
2 二维Helmholtz方程的间接规则化边界积分方程

二维Helmholtz方程的内点边界积分方程为

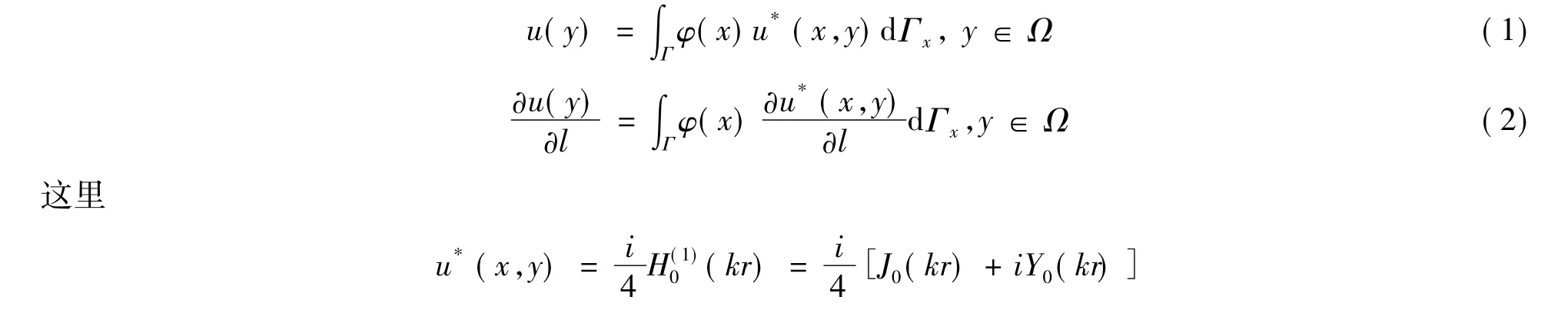
3 数值算例

为了考察结果的准确性，定义相对误差

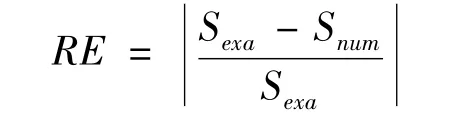
这里，Sexa，Snum分别是计算点处的精确解和数值解。

例1 所考虑的区域为边界条件如下

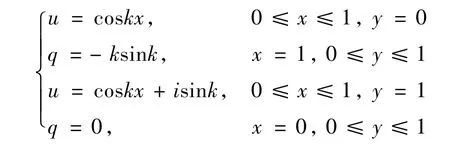
计算时，边界几何采用精确单元描述，边界量采用不连续线性插值逼近。边界被等分成100个单元。当k=1时，表1、2分别给出了域内和边界上u的数值解与精确解的比较。

例2 所考虑的区域是单位圆域:Ω={(x，y)|x2+y2≤1}，边界条件如下

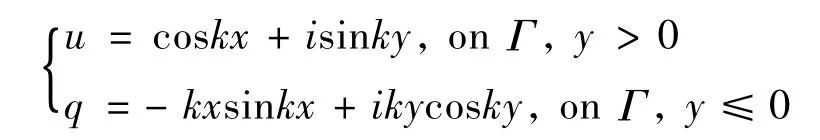
计算时，边界几何采用精确单元描述，边界量采用常元插值逼近。边界被等分成200个单元。当k= 1时，表3、4、5分别给出了单位圆内部u，边界上u、q的数值解与精确解的比较。

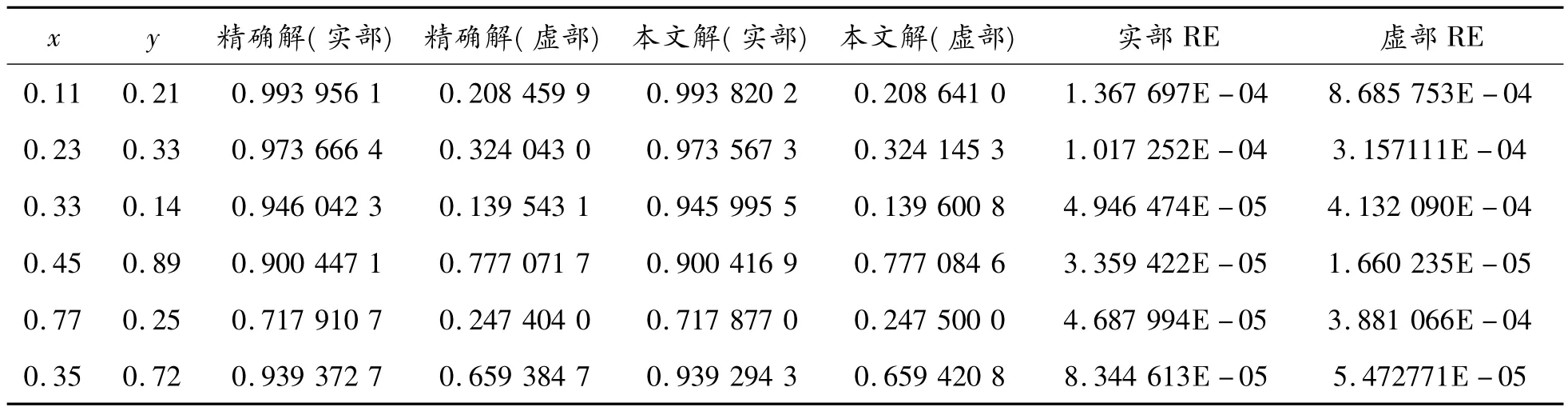
表1 方域内点u的数值解与精确解的比较

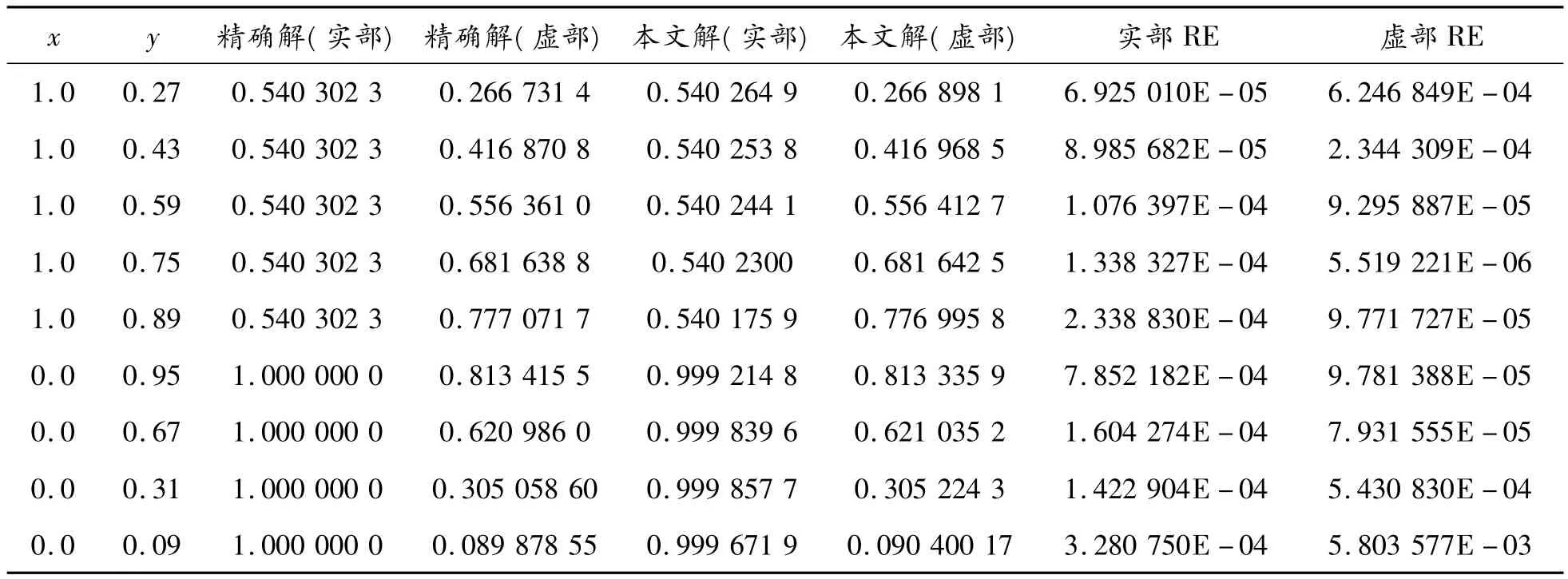
表2 方域边界上u的数值解与精确解的比较

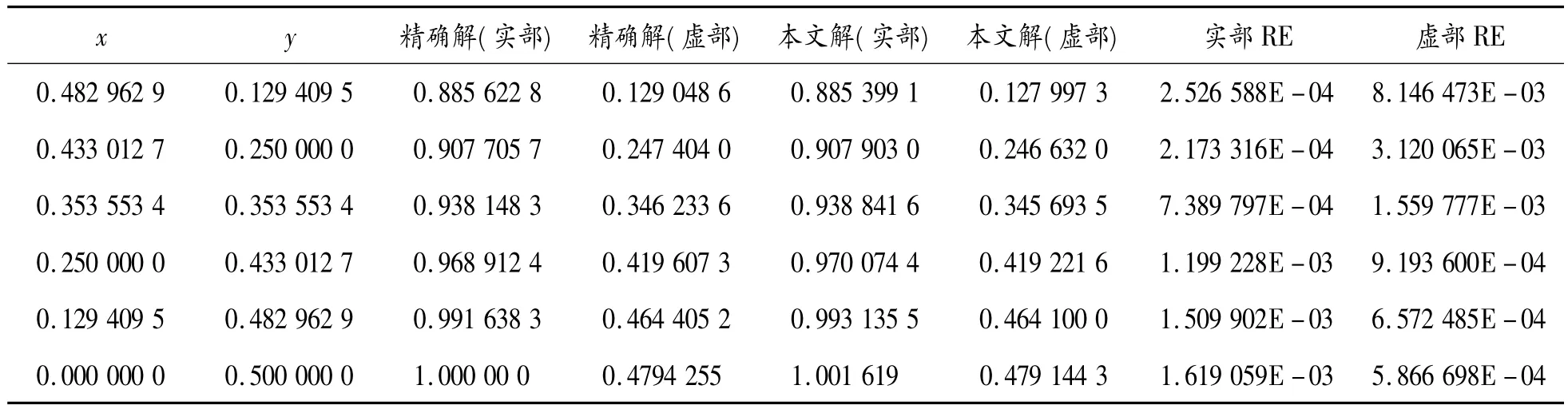
表3 圆域内点u的数值解与精确解的比较

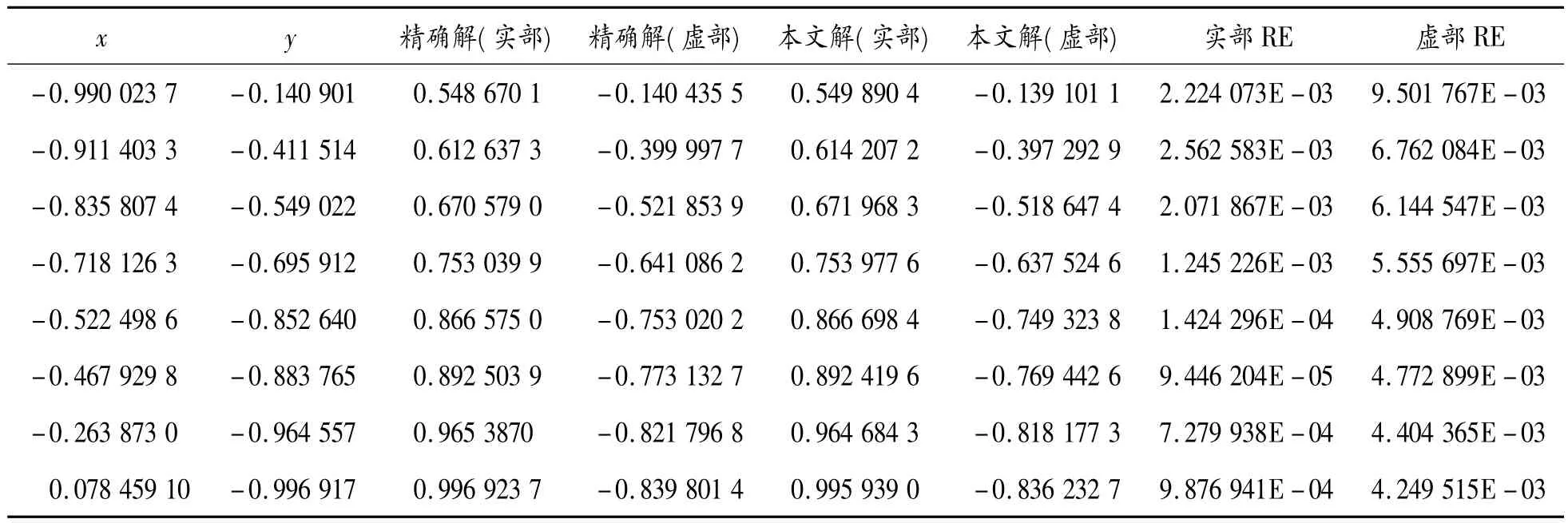
表4 圆域边界上u的数值解与精确解的比较

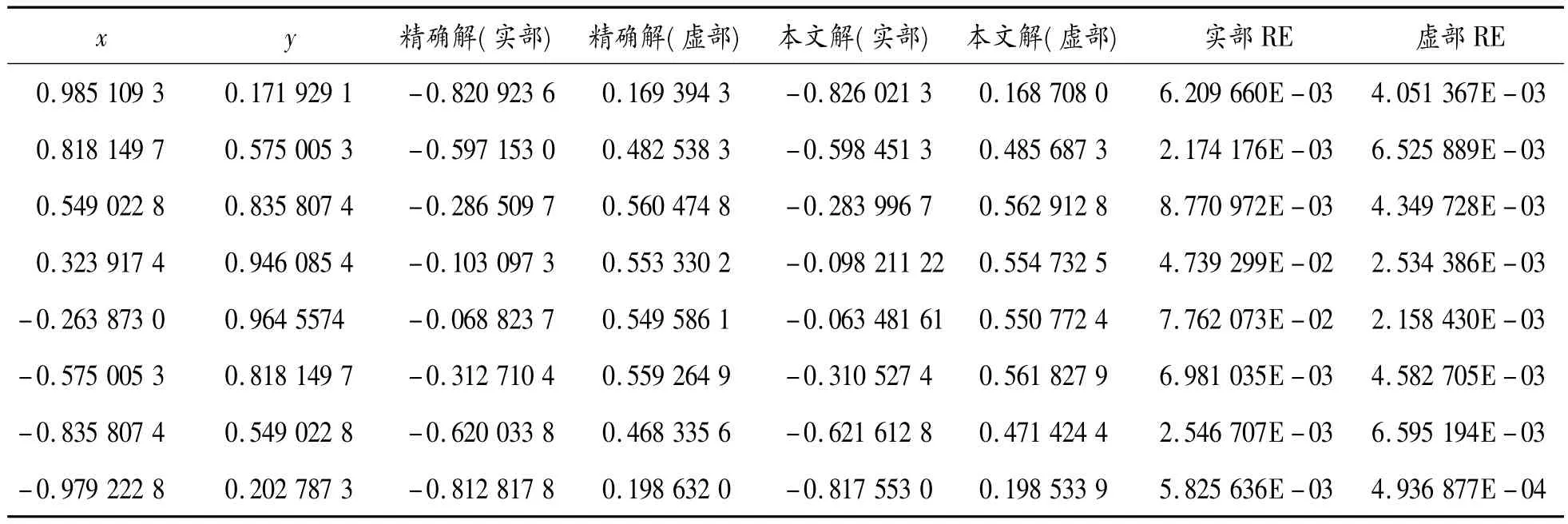
表5 圆域边界上q的数值解与精确解的比较

4 结束语

在已有位势问题的基础上，本文建立了二维Helmholtz方程边值问题的规则化边界积分方程，有效避免了奇异积分的计算，数值算例验证了该方法的可行性。

［1］Jianjun Ma，Jialin Zhu，Maojun Li.The Galerkin boundary element method for exterior problems of 2-D Helmholtz equation with arbitrary wavenumber［J］.Engineering Analysis with Boundary Elements，2010，34(12):1058-1063.

［2］Tomioka S，Nishiyama S.Analytical regularization of hypersingular integral for Helmholtz equation in boundary element method［J］.Engineering Analysis with Boundary Element，2010，34(4):393-404.

［3］Marin L，Lesnic D，Manticˇ V.Treatment of singularities in Helmholtz-type equations using the boundary element method［J］. Journal of Sound and Vibration，2004，278(1/2):39-62.

［4］Harris P J.A boundary element method for the Helmholtz equation using finite part integration［J］.Computer Methods in Applied Mechanics and Engineering，1992，95(3):331-342.

［5］姜欣荣，陈文.基本解方法与边界节点法求解Helmholtz方程的比较研究［J］.计算力学学报，2011，28(3):339-344.

［6］Bin-Mohsin B，Lesnic D.The method of fundamental solutions for Helmholtz-type equations in composite materials［J］.Computers&Mathematics with Applications，2011，62(12):4377-4390.

［7］Marin L.Treatment of singularities in the method of fundamental solutions for two-dimensional Helmholtz-type equations［J］. Applied Mathematical Modelling，2010，34(6):1615-1633.

［8］孙焕纯，张立洲，许强，等.无奇异边界元法［M］.大连:大连理工大学出版社，1999.

［9］Zhang Yaoming，LYU Hexing，Wang Limin.Novel regularized boundary integral equations for potential plane problems［J］.Applied Mathematics and Mechanics，2006，7(9):1165-1170.

(责任编辑何杰玲)

Boundary Element Method for 2D Helmholtz Equation Value Problems

YU Shan-ling，ZHANG Yao-ming
(College of Science，Shandong University of Technology，Zibo 255049，China)

Based on the existing work on potential problems，the indirect regularized BIEs of 2D Helmholtz equation value problems without the calculation of the CPV integrals and the HFP integrals were developed.Numerical examples demonstrate the feasibility and efficiency of this method with low wave number.

2D Helmholtz equation boundary value problems;indirect boundary integral equation;the boundary element method;singular integral

O342

A

1674-8425(2015)11-0139-05

10.3969/j.issn.1674-8425(z).2015.11.024

2015-06-17

山东省自然科学基金资助项目(ZR2010AZ003)

于善玲(1988—)，女，硕士研究生，主要从事应用数学研究;通讯作者张耀明(1962—)，男，博士，教授，主要从事应用数学研究。

于善玲，张耀明.二维Helmholtz方程的边界元法［J］.重庆理工大学学报:自然科学版，2015(11):139 -143.

format:YU Shan-ling，ZHANG Yao-ming.Boundary Element Method for 2D Helmholtz Equation Value Problems［J］.Journal of Chongqing University of Technology:Natural Science，2015(11):139-143.