基于突变级数模型的供应链风险诊断

张云丰，王 勇

(1.安徽工程大学管理工程学院，安徽 芜湖 241000;2.重庆大学经济与工商管理学院，重庆 400030)

由于供应链网络结构错综复杂，外部环境的不确定性和供应链管理者过于追求精益等原因，使得供应链越来越容易遭受各类风险的影响［1］.供应链风险是一种潜在威胁，它会利用供应链系统的脆弱性，对供应链系统造成破坏，给上下游企业以及整个供应链带来损害和损失［2］.近年来，世界范围内各种供应链风险频繁发生，如2005年“苏丹红”事件、2008年“三鹿奶粉”事件及2011年日本地震与海啸等，使企业受到极大的损害.人们已逐渐认识到供应链风险管理的重要性.

学者们主要从4 个方面研究供应链风险管理:风险识别、风险评估、风险管理、风险监控.其中，如何科学评估供应链风险是供应链风险管理的难点，受到了众多供应链管理研究者的关注［3］.Hallikas 等认为，企业间可以通过合作将单个企业的风险纳入整个供应链合作风险中，所提出的半定量化研究方法为供应链风险评估奠定了一定的基础［4］.Wu 等提出了一个层次式供应链风险因子分类与评估模型［5］.Schoenherr 等通过分析一个美国制造企业案例，概括得出供应链风险包含17 种因素并对其分类，提出一个基于层次分析法的供应链中断风险因素评估模型［6］.肖美丹等将未确知理论与模糊评判法相结合，建立基于未确知模糊理论的供应链风险评估模型，并通过数值进行验证［7］.王文婕运用OWA 算子对四级供应链模型进行风险评价，并预测了供应链管理中各风险发生的概率大小和影响大小［8］.陈敬贤基于蒙特卡罗模拟法研究了市场需求波动下的供应链风险估计问题［9］.顾玉磊等借助CVaR 理论构建了一种考虑成员偏好的风险评估模型来度量供应链成员企业风险和整个供应链风险［10］.颜波等采用OWA 算子对农产品供应链风险因素进行重要性排序，筛选出企业所面临的主要风险指标，并应用CVaR 构建风险损失函数，采用改进的遗传算法求解得到风险损失最小的最优风险控制组合［11］.舒彤等构建了供应链风险评估体系，再应用基于支持向量机的机器学习算法对供应链风险进行评估［12］.

上述文献分别建立数学模型对供应链风险进行定量分析，并辅以算例加以说明，具有一定的参考价值.然而我们应该认识到，供应链风险评估是典型的多指标决策问题，在决策过程中需要客观分配各指标的权重，而上述文献有些回避了指标权重的计算(等同于默认所有指标权重相等)，有些通过专家赋权的方式，主观设定指标权重.实际上，指标赋权是一项严谨且复杂的工作.若能设计一种无需计算指标客观权重、决策过程又能体现指标重要程度的评估方法，则评估结果必然更具有说服力.突变级数模型作为多指标决策的一种管理技术，能够很好地满足此要求.

1 突变级数模型基本思想

突变级数模型是数学家托姆创立的一种综合应用拓扑学、奇点理论和结构稳定性等数学工具研究系统行为演变非连续现象的决策方法.其主要思想是根据系统的势函数，把临界点分类，进而研究各种临界点附近非连续性态的特征，即有限个数的若干初等突变，并以此为基础探索自然和社会中的突变现象［13］.势函数f(x)是描述系统的状态变量和控制变量之间相对关系、相对位置的函数.通过对f(x)求一阶导数，并令f '(x)= 0 可以得到该系统所有临界点集合成的平衡曲面方程.该平衡曲面的奇点集可以通过令f ″(x)=0 求得.由f '(x)=0 和f ″(x)=0 可得到由状态变量表示的反映状态变量与各控制变量之间关系的分解形式的分歧点集方程.系统的所有性质都由分歧点集方程决定，当各控制变量的变化不满足该方程时，系统只有量的改变;一旦满足该方程，系统将出现质的改变.利用分歧点集方程与模糊数学相结合推导出突变模糊隶属函数(归一公式)，归一公式将系统内部各控制变量不同的质态归化为可比较的同一种质态.由归一公式对系统进行量化递归运算，最后归一为一个参数，即求出表征系统状态特征的系统总突变隶属度，从而作为系统综合评价的依据.突变级数模型的特点是无需计算指标权重，但它考虑了各评价指标的相对重要性，从而减少了主观性又不失科学性、合理性，而且计算简易准确［14］，在交通流预测、生态环境评估、灾害诊断及众多社会科学领域都得到广泛应用，尤其适用于解决属性权重难以量化的多指标决策和矛盾目标决策问题.

2 基于突变级数模型的供应链风险诊断步骤

结合突变级数模型的基本思想，可按照如下基本步骤进行供应链风险的诊断:

第1 步:构建风险诊断指标体系

按照突变级数模型的要求建立供应链风险诊断指标体系的多层次递阶结构，并对各状态变量所属的控制变量进行重要性排序，将主要控制变量排在前面，次要控制变量排在后面.由于同一状态变量下的多个控制变量的排序会对诊断结果产生重要影响，因此对控制变量进行正确排序显得尤为关键.为了提高排序的科学性，可邀请多名专家参与控制变量排序，并运用Spearman相关系数法处理多名专家给出的排序结果，计算各位专家的平均Spearman 等级相关系数，取最大值视为控制变量最优排序，获得最终的供应链风险诊断评价指标体系多层次递阶结构.

下面给出应用Spearman 相关系数法确定控制变量最优排序的处理过程.现有m 位专家对某状态变量下的n 个控制变量进行重要性排序.设第i 位专家给出的重要性排序向量为则第i 位专家与第j 位专家间的Spearman 等级相关系数表示为:

对ρij加权求和，得到第i 位专家的平均Spearman等级相关系数为:

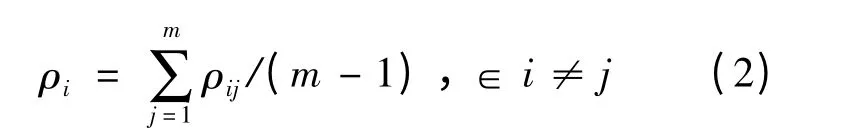
第2 步:获取底层控制变量原始信息，并转化为0 -1 之间的标准数据

在描述底层控制变量的原始信息时，有些可以定量表示，有些只能定性刻画.对于定性刻画的控制变量，考虑到信息的不完全性及风险诊断专家知识的局限等，往往很难用精确数表示其原始信息，而模糊语言有时候更利于风险诊断专家表达自己的偏好.模糊语言的表示主要有区间数、三角模糊数、梯形模糊数、直觉模糊数、语言标度、二元语义等.在决策过程中，虽然选择不同的模糊语言表示及集结方法将会得到不同的结果，但就各种模糊语言表示本身而言并没有优劣之分.下面给出一种模糊语言标度的定义方法.

定义1［15］记Ζ}为模糊语言标度集，ψa表示模糊语言变量.ψ-L和ψL分别表示模糊语言标度集的下限标度和上限标度.若γ = ［ψα，ψβ］，ψα，ψβ∈Ψ 且α＜β，称γ 为模糊语言区间数.当α = β 时，γ 退化为模糊语言变量.

集合Ψ 中元素数量可根据实际评估需要设置.若取L = 4，则集合Ψ 包括9 个元素．在刻画供应链风险时，给定模糊语言变量与风险诊断专家表达的模糊偏好信息存在如下对应关系:ψ-4=VL(很低)，ψ-3= L (低)，ψ-2= ML (较低)，ψ-1= FL(稍低)，ψ0= IG(一般)，ψ1= FH(稍高)，ψ2= MH(较高)，ψ3= H(高)，ψ4= VH(很高).

由于模糊语言区间数不能直接带入突变级数模型计算，因此需要通过转换公式将之转化后方可进行.通过定义2 可实现模糊语言区间数与精确数之间的转化.

定义2 记γ = ［ψα，ψβ］为模糊语言区间数，Θ 为精确数，其中α，β ∈［-L，L］，0 ≤Θ ≤1 .存在下列对应法则使得映射关系f:{［Ψα，Ψβ］}→Θ 成立:

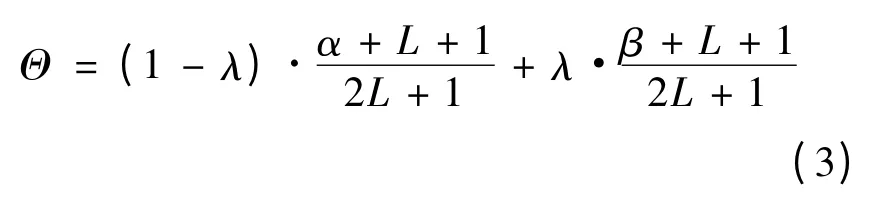
其中，λ 表示风险诊断专家对风险程度的偏好.若λ = 0 ，说明风险诊断专家对风险持乐观态度;若λ = 1 ，说明风险诊断专家对风险持悲观态度.Θ 可理解为风险系数，Θ 越小，说明风险程度越低.

第3 步:确定各层次状态变量的突变级数模型类型

数学上已经证明，当状态变量不多于2 个、控制变量不多于5 个时，自然界的初等突变级数模型已达11 种形式.状态变量为1 个时，常见的初等突变模型有5 个，分别为:

折叠突变级数模型:f1(x)= x3+ a1x;

尖点突变级数模型:f2(x)= x4+a1x2+a2x;

燕尾突变级数模型:f3(x)= x5+a1x3+a2x2+ a3x;

蝴蝶突变级数模型:f4(x)= x6+a1x4+a2x3+ a3x2+ a4x;

棚屋突变级数模型:f5(x)= x7+a1x5+a2x4+ a3x3+ a4x2+ a5x．

其中，x 为待评估系统的状态变量，f(x)为状态变量x 的势函数，a1～a5为状态变量x 所属的控制变量.若一个状态变量包含一个控制变量，则可视为折叠突变级数模型;若一个状态变量包含两个控制变量，则可视为尖点突变级数模型.对于控制变量大于5 的情形，传统的做法是进行指标提纯或降维，使得每个状态变量所属的控制变量不超过5 个，以便于能够应用上述5 种初等突变级数模型处理，但这种方式容易丧失事物本身反映的真实信息.观察上述5 种初等突变级数模型势函数表达式可知，初等突变级数模型势函数的一般表达式为:

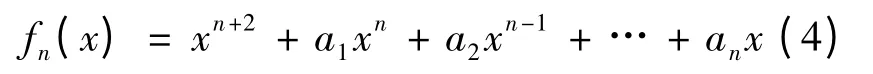
根据(3)式就可以将初等突变级数模型推广到控制变量n(n ＞5)个的情形.

第4 步:由分歧点集方程导出归一公式，进行逐层量化递归运算

对势函数fn(x)依次求n 阶导数，并分别令其等于0.先由f(n)n(x)= 0 解得a1(x)，再带入解得a2(x).通过逆向归纳法可顺次解得a3(x)～an(x)，即得到分歧点集方程.对分歧点集方程作变量替换解得x(an)的表达式，再换回原变量即为归一公式.如对尖点突变级数模型有f2'(x)= 4x3+2a1x +a2= 0、f2″(x)=12x2+2a1= 0 ，解得a1(x)= - 6x2、a2(x)=8x3.令t1= - a1/6 、t2= a2/8 ，则有x(t1)=换回原变量得到x(a1)= a11/2、x(a2)= a1/32.

将控制变量的标准数据带入相应归一公式，便可解得控制变量的突变隶属度.结合多目标模糊决策理论可知，由下层诸控制变量的突变隶属度决策上层状态变量的突变隶属度时，若诸控制变量之间不存在明显的相互关联作用，称诸控制变量为“非互补”关系，这时应遵从“取小原则”，即xi= min{xi(a1)，xi(a2)，…，xi(an)}.若诸控制变量为“互补”关系，则应遵从“平均原则”，即xi= aver{xi(a1)，xi(a2)，…，xi(an)}.

第5 步:根据系统总突变隶属度，诊断供应链风险等级

经过逐层量化递归运算得到系统总突变隶属度后，若能将之与标准供应链风险等级表对照，便可诊断出供应链的风险等级.令人遗憾的是，目前尚没有供应链风险等级划分的固定标准.不同的评估方法由于决策机理不同，划分的各风险等级上下临界值也不相同，文献［3，6，16］分别建立了供应链风险等级的划分标准.本文在参考上述文献划分标准的基础上，根据风险系数值Θ 所属区间对供应链风险按4 个等级划分如下:若Θ ∈［0，0．4)，则为低风险;若Θ ∈［0．4，0．7)，则为中等风险;若Θ ∈［0．7，0．9)，则为高风险;若Θ∈［0．9，1］，则为极大风险.由于突变级数模型诊断结果需要通过总突变隶属度判断，因此必须建立风险系数值Θ 与总突变隶属度之间的对应关系.对于任意层次的指标体系，给定风险系数值Θ ∈［e1，e2］，设底层所有指标的风险系数值Θi= e1时，系统总突变隶属度为X1;至少有1 个底层指标的风险系数值Θk≠e1时，系统总突变隶度为X'1.其中，Θi、Θj分别表示第i、k 个控制变量的风险系数值.数学上可以证明，必有X1≤X'1.显然，当底层指标的风险系数值Θ ∈［e1，e2］时，对应的系统总突变隶属度X ∈［X1，X2］.因此，结合风险诊断指标体系，将不同风险等级的风险系数临界值带入归一公式，通过逐层递归计算，便可以得到以系统总突变隶属度表示的供应链风险等级.

3 风险诊断算例研究

本部分将应用突变级数模型对供应链存在的风险进行科学诊断.首先需要建立风险诊断指标体系.根据科学性、层次性、可比性、全面性、可操作性等指标设计的基本原则，在总结文献［1，3，8，12］研究成果的基础上，本文提出一个包括5 个一级指标、16 个二级指标的供应链风险诊断指标体系:(1)供应风险，含产品价格风险、产品质量风险、供应商交货风险、生产柔性风险4 个二级指标;(2)需求风险，含需求波动风险、客户流失风险2 个二级指标;(3)信息风险，含信息共享风险、信息传递风险、信息失真风险3个二级指标;(4)财务风险，含收益分配风险、企业资金风险2 个二级指标;(5)环境风险，含自然风险、社会风险、经济风险、政治风险、文化风险5 个二级风险.为了确定5 个一级指标的重要性排序，邀请7 位专家进行群组决策，分别赋予的重要性排序向量如表1所示.

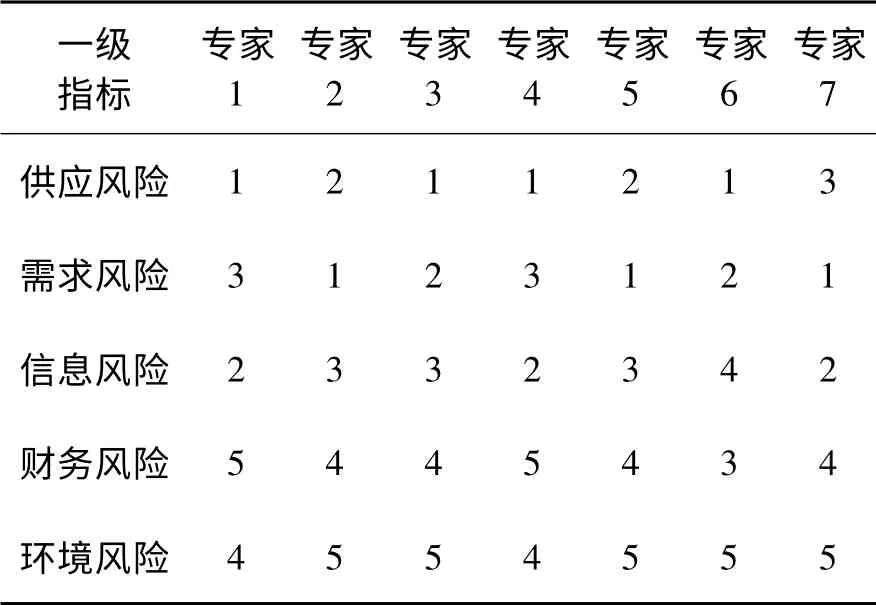
表1 一级指标重要性排序

根据Spearman 相关系数等级计算公式，有ρ1= ρ4= ρ6= 0．667 ，ρ2= 0．783 ，ρ3= 0．833，ρ5= 0．800 ，ρ7= 0．650 .因此，专家3 赋予的一级指标重要性排序结果最优.同理可计算出各二级指标的平均Spearman 等级相关系数.各级指标最终的重要性排序、底层指标原始信息及经转化后的标准数据如表2所示.

供应风险有4 个二级指标，属于蝴蝶突变级数模型，指标之间属于“非互补关系”，采用“取小原则”，故供应风险的突变隶属度为:

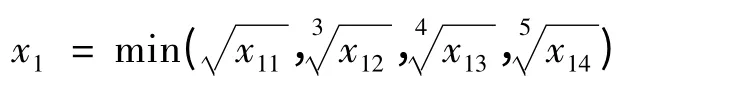
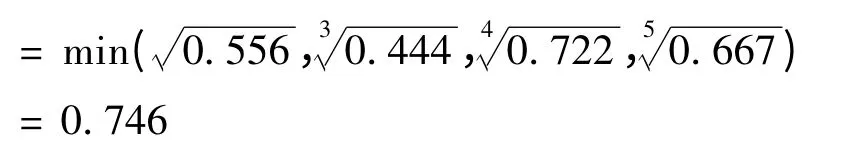
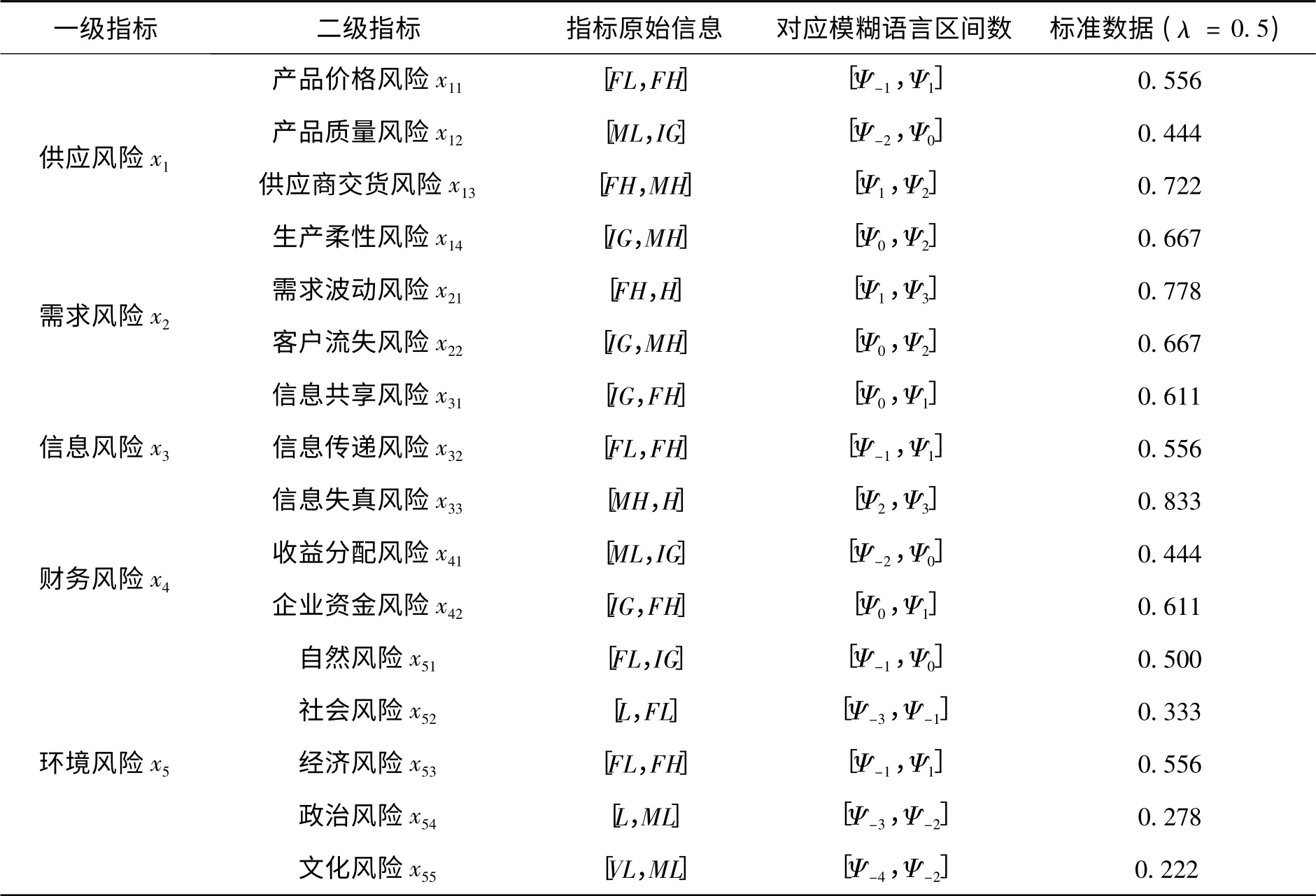
表2 指标重要性排序、原始信息及标准数据

需求风险有2 个二级指标，属于尖点突变级数模型，指标之间属于“非互补关系”，采用“取小原则”，故需求风险的突变隶属度为:

信息风险有3 个二级指标，属于燕尾突变级数模型，指标之间属于“互补关系”，采用“平均原则”，故信息风险的突变隶属度为:

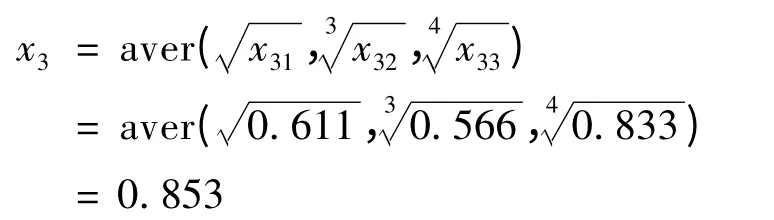
财务风险有2 个二级指标，属于尖点突变级数模型，指标之间属于“互补关系”，采用“平均原则”，故财务风险的突变隶属度为:

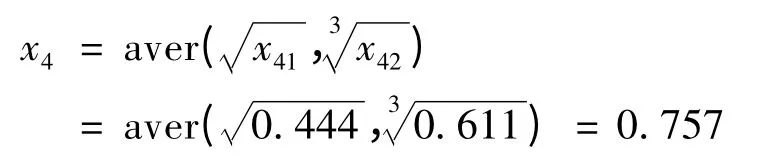
环境风险有5 个二级指标，属于棚屋突变级数模型，指标之间属于“非互补关系”，采用“取小原则”，故环境风险的突变隶属度为:

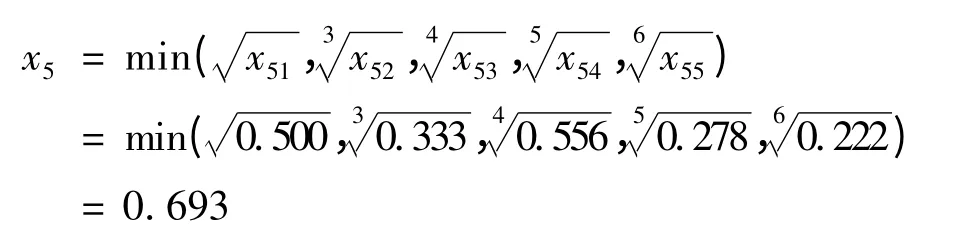
供应链风险诊断指标体系包括5 个一级指标，属于棚屋突变级数模型，指标之间属于“非互补关系”，采用“取小原则”，故系统总突变隶属度为:

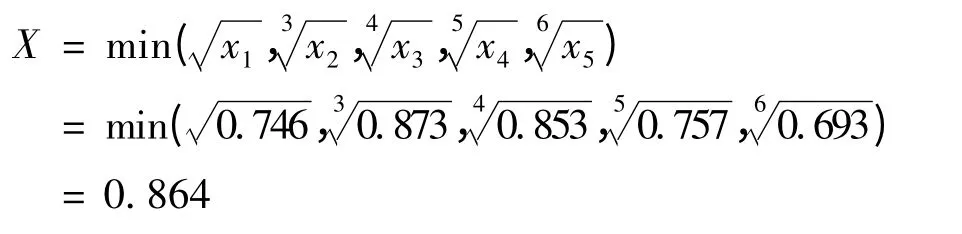
结合本文建立的供应链风险诊断指标体系，将不同风险等级的风险系数临界值带入归一公式，通过逐层递归计算，得到系统总突变隶属度X 与风险等级的对应关系为:若X ∈［0，0．795)，则为低风险;若X ∈［0．795，0．915)，则为中等风险;若X ∈［0．915，0．974)，则为高风险;若X ∈［0．974，1］，则为极大风险.由于系统总突变隶属度为0.864，因此可以认定供应链处于中等风险等级.

4 敏感性分析

上述诊断过程中，假设风险诊断专家持风险中立态度(即λ = 0．5 ).然而实际决策中，不同的风险诊断专家可能有不同的风险偏好程度.为了检验风险偏好程度λ 对诊断结果的影响，我们计算不同风险偏好程度λ 值下的系统总突变隶属度，并诊断相应的风险等级，具体结果如表3所示.

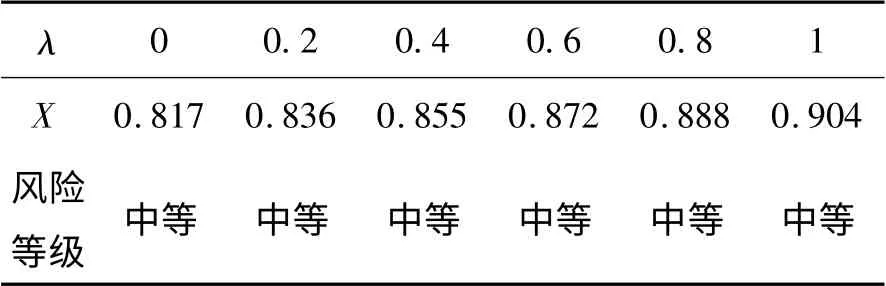
表3 风险偏好对风险等级的敏感性分析

通过表3可以看出，风险诊断专家的风险偏好程度对风险等级的诊断不敏感.这也进一步表明本文提出方法的合理性.

5 结语

现有供应链风险诊断方法要么受主观因素影响，要么计算比较复杂，且对指标权重的分配过于随意.考虑到这些方法的局限性，本文结合突变理论思想，提出一种基于突变级数模型的供应链风险诊断方法.虽然突变级数模型在其它领域已被尝试用于多指标决策问题，但本文首次将突变级数模型引入供应链领域，进一步拓宽了突变级数模型的应用范围.

本文应用突变级数模型的同时，在方法上实现了如下创新:(1)关于控制变量重要性排序.结合群决策思想和Spearman 相关系数法来确定控制变量的排列次序，将决策的主观性因素降到最低.(2)关于底层指标赋值.供应链风险指标大多为定性指标，导致用精确数度量它们非常困难.本文采用模糊语言区间数来刻画指标，并考虑到风险诊断专家的风险偏好态度对风险等级可能存在的影响，给出敏感性分析.(3)关于风险等级划分.现有文献对风险等级的划分主要是把综合风险系数线性均分为几个区间，而本文则根据供应链风险突变的内在决策机理来划分，因而风险等级划分标准更科学.

［1］张毕西，陈嘉.基于灰色多层次评价模型的供应链风险评估［J］.科技与管理，2011，13(5):56 -59.

［2］丁伟东，刘凯，贺国先.供应链风险研究［J］.中国安全科学学报，2003，13(4):64 -66.

［3］彭国樑，姚俭.不确定性供应链风险的模糊综合评价［J］.上海理工大学学报，2010，32(4):373 -377.

［4］Hallikas J，Karvonen I，Pulkkinen U，et al.Risk process in supplies networks［J］.International Journal of Production Economics，2004，90(1):47 -58.

［5］Wu T，Blackhurst J，Chidambaram V.A model for inbound supply risk analysis［J］.Computers in Industry，2006，57(4):350 -365.

［6］Schoenherr T，Raotummala V M，Harrison T.Assessing supply chain risks with the analytic hierarchy process:providing decision support for the offshoring decision by a US manufacturing company［J］.Journal of Purchasing and Supply Management，2008，14(2):100 -111.

［7］肖美丹，李从东，张瑜耿.基于未确知模糊理论的供应链风险评估［J］.软科学，2007，21(5):27 -30.

［8］王文婕.基于OWA 算子的供应链风险评估方法［J］.物流技术，2011，30(7):110 -113.

［9］陈敬贤，施国洪，程发新.基于蒙特卡罗模拟的供应链风险估计研究［J］.数学的实践与认识，2011，41(13):1 -9.

［10］顾玉磊，张圣忠，吴群琪.基于成员企业偏好的供应链风险评估模型［J］.科技管理研究，2013，33 (2):195 -199.

［11］颜波，石平，王凤玲.基于CVaR 的农产品供应链风险评估与控制［J］.软科学，2013，27(10):111-115.

［12］舒彤，葛佳丽，陈收.基于支持向量机的供应链风险评估研究［J］.经济经纬，2014，31(1):130 -135.

［13］李柏洲，苏屹.基于改进突变级数的区域科技创新能力评价研究［J］.中国软科学，2012(6):90 -101.

［14］陈晓红，杨立.基于突变级数法的障碍诊断模型及其在中小企业中的应用［J］.系统工程理论与实践，2013，33(6):1479 -1485.

［15］徐泽水.基于语言信息的决策方法和理论［M］.北京:科学出版社，2008.

［16］蒋有凌，杨家其，尹靓，等.基于ANN 的供应链风险综合评估模型与应用［J］.武汉理工大学学报:交通科学与工程版，2008，32(1):70 -73.