Strength criterion for rocks under compressive-tensile stresses and its application

Mingqing You

School of Energy Science and Engineering,Henan Polytechnic University,Jiaozuo,454010,China

Strength criterion for rocks under compressive-tensile stresses and its application

Mingqing You*

School of Energy Science and Engineering,Henan Polytechnic University,Jiaozuo,454010,China

A R T I C L EI N F O

Article history:

Received 17 January 2015

Received in revised form

16 May 2015

Accepted 20 May 2015

Available online 16 June 2015

Strength criteria

Tensile strength

Exponential criterion

Hydraulic fracturing

Estimating in-situ stress with hydraulic borehole fracturing involves tensile strength of rock.Several strength criteria with three parameters result in tensile strengths with great differences,although they may describe the relation between strength of rock and confning pressure with low misfts.The exponential criterion provides acceptable magnitudes of tensile strengths for granites and over-estimates that for other rocks,but the criterion with tension cut-off is applicable to all rocks.The breakdown pressure will be lower than the shut-in pressure during hydraulic borehole fracturing,when the maximum horizontal principal stress is 2 times larger than the minor one;and it is not the peak value in the frst cycle,but the point where the slope of pressure-time curve begins to decline.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

Numerous tests have been carried out to determine the strengths of rocks under confning pressure(CP),as rocks in-situ are usually under compression state.However,tension usually appears in the vicinity of excavation and borehole,and the tensile strength of each rock is much lower than the compressive strength.

The direct tension test is diffcult to perform for rock(You et al., 2006).In other hand,the Brazilian splitting test with rock disc is easy tocarryout in laboratoryand provides a reasonable estimation for the uniaxial tensile strength(UTS),although there are many issues argued all along(Fairhurst,1964;Hudson et al.,1972;Efmov, 2009;Yu et al.,2009;You et al.,2011).

Many strength criteria have been proposed to describe the state of stresses in rock at failure,as reviewed in Yu(2002)and You (2011).Clearly,an ideal strength criterion needs to closely ft test data with acceptable accuracy over the stress state expected in practice.Therefore,the tensile strength predicted by a strength criterion is usually used in evaluating the criterion(Ghazvinian et al.,2008;Bineshian et al.,2012).Tensile strengths predicted by both the Coulomb criterion and the Griffth criterion are much higher than the measured magnitudes of almost all rocks,although the two criteria have clear physical backgrounds(Jaeger et al., 2007).

Another issue is the effect of compressive stress on tensile strength,i.e.strength criterion in tension-compression region.It has practical utilization in the in-situ stress estimation with hydraulic breakout of borehole and some cases of wellbore stability.

This paperdiscusses fourcriteriawith three material-dependent parameters using test data of nine rocks from the published literature.The exponential criterion with tension cut-off is recommended and adopted to estimate in-situ stress with hydraulic borehole fracturing.

2.Strength criteria

Coulomb criterion was initially proposed in 1773 for determination of the shear strength of soil,and introduced for rocks later.It is a linear equation with the principal stresses as

whereσSis the major principal stress or rock compressive strength, σ3is the minor principal stress,σCis the uniaxial compressive strength(UCS),andmis a material-dependent parameter.However,test results from cylindrical specimens of rocks compressed under CP ofσ2=σ3exhibit convex curves of strength.Therefore, many nonlinear criteria were proposed as modifcations to the Coulomb criterion,and briefy reviewed as follows.

Hobbs(1964)proposed an empirical criterion with three parameters:

Its special case atm=2 andn=1/2 is the normal parabolic criterion(You,2011):

The criterion with one parameter merely fts strengths of granular rocks better than the Coulomb criterion,nearly the same as the Hoek-Brown(H-B)criterion with two parameters.

The Murrell criterion(Murrell,1965)was widely used atn=0.5 (Mogi,2007):

The two criteria,Eqs.(2)and(4),are not applicable to negative σ3for power numbernis less than 1,and are certainly beyond the consideration for compressive-tensile strength.

The Sheoreycriterion(Sheoreyet al.,1989)normalized with UCS is given in the following form:

The criterion proposed in Carter et al.(1991)is in the similar form.The derivative ofσStoσ3for Eq.(5),and Eq.(4)as well,will be less than 1 whenσ3is large enough.That means the differential stressσS-σ3will decrease with increasing CP.The phenomenon appears really for Solnhofen limestone(Mogi,2007),and Indiana limestone(Schwartz,1964)as well,within the test range of CP,as illustrated by You(2011).It is totally different from the common knowledge.

The most famous criterion inpower form is the generalized H-B criterion(Hoek et al.,1992):

The specifc form atn=1/2 is called the H-B criterion(Hoek and Brown,1980)that has been widely used in rock engineering (Eberhardt,2012).The criterion fails to describe strength of ductile rocks,such as limestone and marble under high CP.

Cohesion and friction in rocks do not act simultaneously at one point,and the cohesion will be replaced by the frictional resistance when crack initiates in the rock under compression(You,2005a). The intact rock under shearing will yield and lose its cohesion,but cracks do not slide macroscopically to increase the friction to the maximum when CP is high enough.The differential stressσS-σ3,or the maximum shear stress equivalently,has an upper limitation in rocks,and is able to be described with a general criterion(You, 2012):

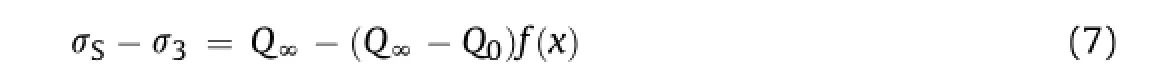
whereQ0is the UCS;Q∞is the limitation of differential stress when CP increases up to infnite;f(x)is a monotonically decreasing function,and satisfesf(0)=1,f(∞)=0,andf′(0)=-1;andxcan be written as

whereK0is the increasing rate of strength atσ3=0.

The exponential criterion(You,2009,2010a)is a specifc case of Eq.(7)at

The fractional form for Eq.(7)is equivalent to the criterion in Rafai(2011)and Bineshian et al.(2012),and the later manifested that the criterion was originally proposed in Bineshian(2000).In this paper,we called it as the fractional criterion,which is just parallel to the exponential criterion mentioned above.

3.Fitting solutions of strength criteria and tensile strengths predicted

In strength criteria,there are always material-dependent parameters,which are determined by ftting the criteria to test data. Test data of nine rocks,presented in Table 1,including granite, limestone,marble,sandstone,and halite,are cited from the literature(Von Kármán,1911;Schwartz,1964;Carter et al.,1991; Haimson and Chang,2000;Sriapai,2010;You,2010a)to evaluate the strength criteria.Averagemagnitude of strengthswith the same CP is used as one datum.

Different solutions of ftting the criteria to test data will be obtained using various statistical methods.The least square method is mostly used for the convenience in mathematical calculation,but the ftting solution will depart signifcantly from normal data to reduce the squares deviation of abnormal data with huge error. Linear regression for a transformed equation of the H-B criterion may result in an imaginary number of UCS(You,2010a,2012). Therefore,the ftting solution on the least absolute deviation,i.e. the least mean misft,is chosen in this paper.

The average values of the mean misfts for nine rocks are 2.9 MPa,2.9 MPa,3.1 MPa,and 3.5 MPa using the Sheorey criterion, the fractional criterion,the exponential criterion,and the generalized H-B criterion,respectively.Each criterion provides the least mean misfts for some rocks.The exponential criterion is the best one for three rocks.

Certainly,the misft is not the single standard to evaluate strength criteria.As illustrated in You(2010a,2012),the exponential criterion may expose a few abnormal data of Mizuho trachyte and Jinping sandstone with huge misft.A new example of Maha Sarakham halite(Sriapai,2010)is shownin Figs.1 and 2.Clearly,the misft of the exponential criterion is mainly pronounced for two data indicated withAandB,as shown in Fig.1.At least,datumAmay be pointed as an abnormal one.If the datum is deleted,thenthe ftting solution using the exponential criterion is almost the same,but the mean misft decreases from 1.3 MPa to 0.9 MPa.

Table 1Test data of conventional triaxial compression of nine rocks.

The fractional criterion,bold line in Fig.2,also presents a low misft for the halite,but misft is distributed in four data,indicated withA,B,CandD,located in two sides of the ftting solution.If the datumAis deleted,then the ftting solution,thin line in Fig.2,has a signifcant change,but the mean misft only decreases from1.5 MPa to 1.4 MPa.Compared to the ftting solution using the exponential criterion as shown in Fig.1,the fractional criterion seems not to well describe the strengths under high CPs;hence,the limitation of differential stress from the fractional criterion,Q∞presented in Fig.2,has lower confdence than that from the exponential criterion.

The UTSs predicted by the ftting solutions of four criteria are presented inTables 2 and 3.The measured tensile strengths of eight rocks with Brazilian test are also presented.The tensile strengths of Westerly granite and Carrara marble are cited from Cai(2010)and Ramsey and Chester(2004),respectively.

The Sheorey criterion and the generalized H-B criterion predict reasonable tensile strengths only for Tyndall limestone and Indiana limestone,respectively.Except for a few rocks,the tensile strengths predicted by the two criteria are lower than the measured magnitudes.The ratios of UCS to UTS predicted by the generalized H-B criterion are 10.6-63 with an average of 31.8 as presented in Table 3,which is much higher than the practical value.

Both Rafai(2011)and Bineshian et al.(2012)extended envelopes of the fractional criterion to tension range.The later argued that the criterion described tensile strengths well,but only test results of coal were presented.As listed in Table 2,however,the fractional criterion presents reasonable UTS values only for Westerly granite and Zhaogu sandstone.

The exponential criterion provides reasonable UTS for four rocks:Bonnet granite,Westerly granite,Zhaogu sandstone,and Georgia marble.The tensile strength predicted by the exponential criterion is 6%lower than the measured magnitude for Bonnet granite,and higher than that of the other rocks,as presented in Table 2.It may be concluded that the exponential criterion tends to overestimate tensile strengths for rocks.

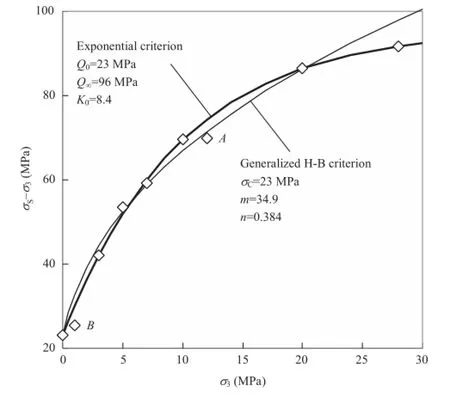
Fig.1.Fitting solutions using the exponential criterion and the generalized H-B criterion for Maha Sarakham halite.

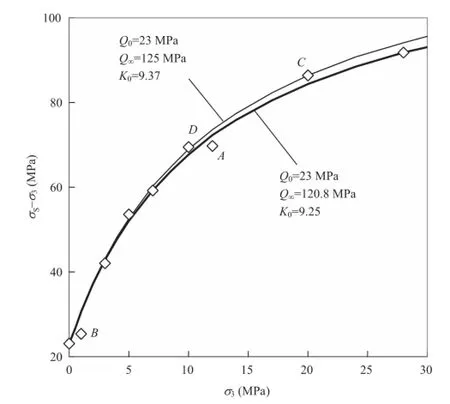
Fig.2.Fitting solutions using the fractional criterion for Maha Sarakham halite.The thin line is for test data to the exclusion of datumA.

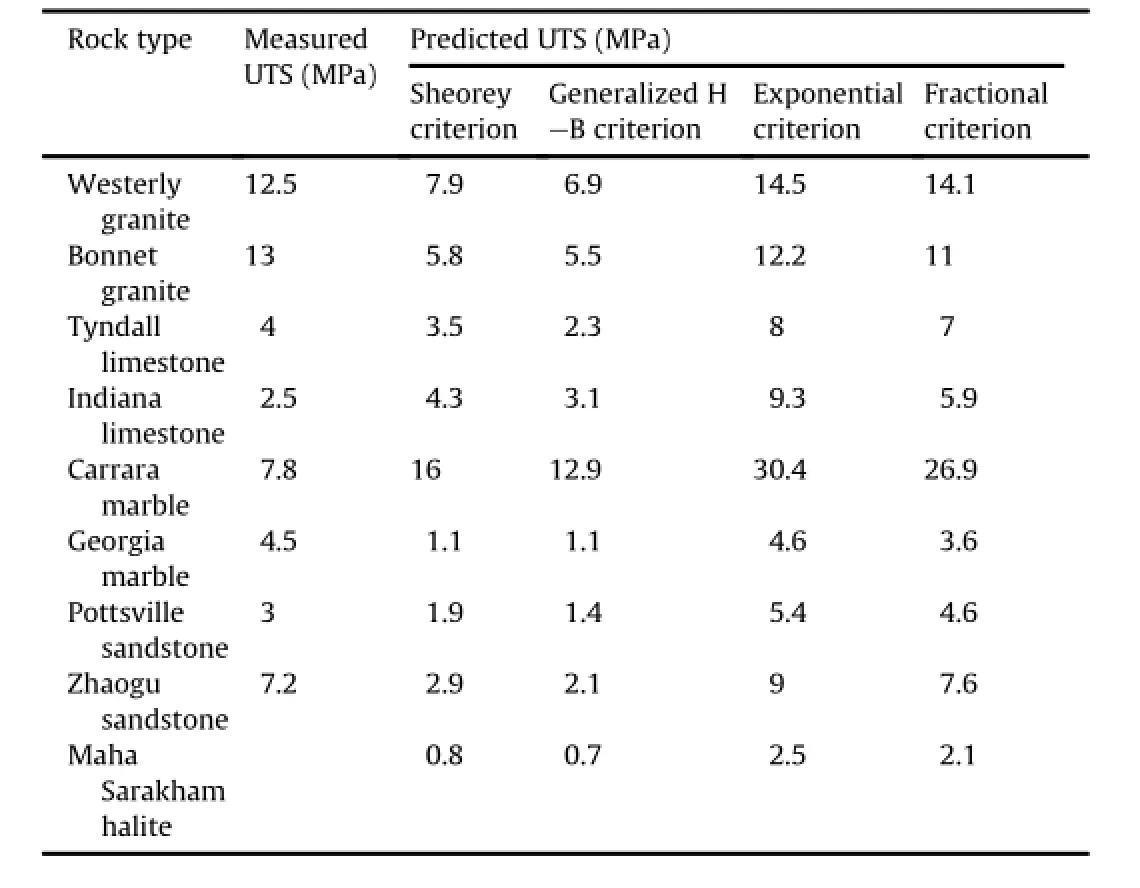
Table 2Measured UTSs and the magnitudes predicted by four strength criteria.

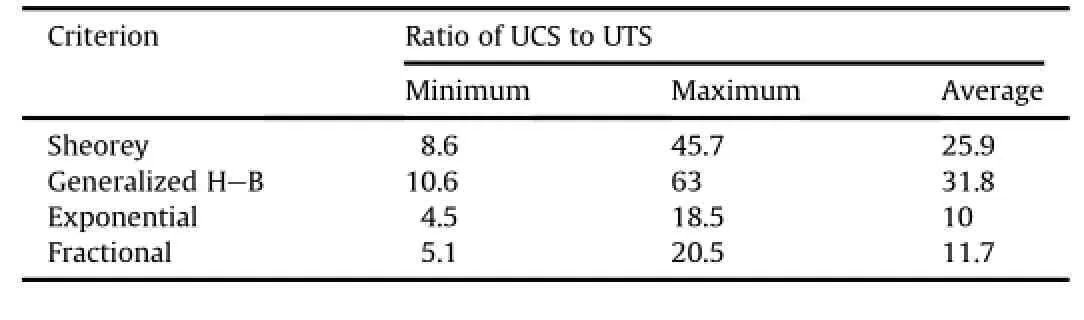
Table 3Ratios of UCS to UTS predicted by four strength criteria.

4.Strength criterion for rocks under compressive-tensile stresses

The four criteria have nearly the same average magnitudes of mean misft for nine rocks.However,UTSs predicted by the four criteria have great difference,as presented in Table 2.Clearly,the magnitudeTof UTS is an independent parameter for rock to bedetermined from test;and it is impossible to describe strength for all rocks under compressive-tensile stresses by simply extending a criterion that is optimized from compression test data.

As the measured tensile strength of Bonnet granite,the merely one case,is slightly larger than the predicted value obtained from the exponential criterion,we may consider that the entireenvelopeoftheexponentialcriteriondescribesthe strength of Bonnet granite under compression-tension on the safety side,as shown in Fig.3.For other rocks,e.g.Zhaogu sandstone as shown in Fig.4,the exponential criterion with a tension cut-off atσ3=-Tis able to describe strength of rocks under compressive-tensile stresses.The exponential criterion is applicable low toσEfor the major principal stress as shown in Fig.4.

Tensile strengths predicted by the Sheorey criterion and the generalized H-B criterion,however,are much lower than the measured magnitudes for many rocks,such as Bonnet granite, Zhaogu sandstone,and Georgia marble,as presented inTable 2,and so does the fractional criterion for Georgia marble and Bonnet granite.Therefore,the tension cut-off is not applicable to the three criteria mentioned above.

It should be noted that the strengths of rock especially under low CPs are always dispersed,e.g.six UCSs of Zhaogu sandstone are from 119.7 MPa to 142.9 MPa,as shown in Fig.4.Therefore, improvement for the tension cut-off as illustrated in You(2012) may not be necessary.

The envelope of the exponential criterion for rocks under compressive-tensile stresses is illustrated nearly as a straight line for the variablexin the range of-T≤σ3≤0 for all rocks:

in the range of-T≤σ3≤0 for all rocks.Therefore,we may use Eq. (11)instead of the exponential criterion in the tension range to simplify the calculation.The equation is not the Coulomb criterion, but the tangent line of the exponential criterion atσ3=0.The parameterK0is always larger than that in the Coulomb criterion. Tension cut-off is atσE=Q0-K0T,and tensile strength under compressive stress in the range ofσE≤σ1≤Q0is

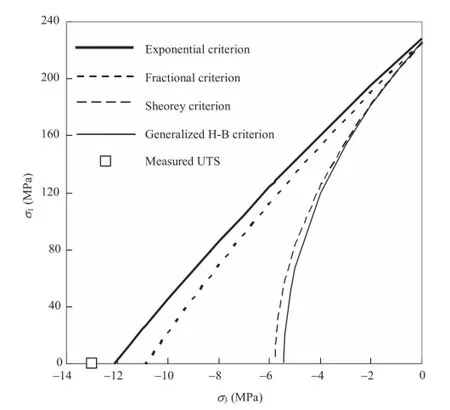
Fig.3.Envelopes of four criteria for rock under compressive-tensile stresses.The criteria are optimized from fracture strengths of Bonnet granite.

Fig.4.Exponential criterion with a tension cut-off for Zhaogu sandstone.

Strength criteria mentioned above do not consider the effect of the intermediate principal stress.In fact,the commonly utilized tension test under CP,also known as triaxial extension test, is conducted in a stress state ofσ3＜0＜σ2=σ1(Ramsey and Chester,2004;You,2010b),but the extension of conventional triaxialcompressioncriteriontothetensilestressmeans σ3=σ2＜0＜σ1,for which there is indeed no test result available for rocks.

The biaxial compression strength is not equal to the UTS; therefore,the intermediate principal stress has more or less infuence on the strength when the minor principal stress is negative.However,as the tensile strength of rock is much lower than the UCS,the minor principal stress with a negative magnitude,i.e.tensile stress,will not be signifcantly infuenced by the intermediate principal stress at a given major principal stress.

5.Hydraulic fracturing of rocks

Hydraulic fracturing is a borehole feld test designed to assess the state of in-situ stress in the earth crust.The overburden stressσzisthoughtof as acting along the vertical direction,and theothers on the horizontal plane namedσHandσh,are calculated using three parameters,i.e.breakdownpressurePb,re-opening pressurePr,and shut-in pressurePsobtained from the pressure-time curve.

The fracture induced hydraulically closes back at shut-in pressure

after the pump is shut off.It is strongly recommended that more than one method be used for obtaining the crucialPs(Haimson and Cornet,2003).The re-opening pressure

is also relative to the determining techniques,as it is not the peak value,but the point on the ascending portion of the pressure-time curve in subsequent cycles,where the slope begins to decline from that maintained in the breakdown cycle.

The breakdown pressurePbis an identifed magnitude taken as the peak pressure attained in the frst pressure cycle.In the ISRM suggested methods(Haimson and Cornet,2003),it can be written as

which means that the major principal stressσ1does not infuence the tensile failure of rock.However,it should involve strength criterion in compression-tension region.Based on the elastic fracture mechanics,the far-feld tensile stress and inner pressure,i.e.pore pressureP0,have the same effect on the Griffth crack(You,2005b), therefore the breakdown pressure is

whereσ1is lower than the UCS,and parametersQ0andK0come from the exponential criterion,as illustrated in Fig.4 and Eq.(13). This provides another magnitude for 3σh-σH,based on the reopening pressurePr.

As mentioned above,the breakdown pressurePbis the peak pressure in the frst pressure cycle.This implies an assumption thatPb＜PSorPb＜σh.Hence,the stresses must satisfy

The pore pressure is not lower than the static hydraulic pressure at the test interval,which is 10 MPa at a depth of 1000 m.The tensile strength of rock is around and usually lower than 10 MPa. Therefore,the magnitude of right side of Eq.(18)is around zero.

Certainly,the stress magnitudes obtained from hydraulic fracturing always satisfy Eq.(18).Stresses from fve boreholes(Chen et al.,2004;Tan et al.,2004;Kang et al.,2007)are in the region ofσH＜2σh,as presented in Table 4.

Table 4In-situ stresses measured with hydraulic fracturing test.

Table 5In-situ stresses measured with overcoring test.

However,the real in-situ stresses may be different from Eq.(18). For example,the in-situ stresses measured with overcoring test (Pine et al.,1983;Anderson andChristianson,2003;Tan et al.,2004; Cai et al.,2010)may exhibit large magnitudes ofσH-2σh,as presented inTable 5.Furthermore,magnitudes of 3σh-σHare negative at test locations in the South Crofty and Oskarshamn.The borehole should break under pore pressure about 5 MPa,not need pump pressure at all,if it was poured with water.The borehole of Ertan at a depth of 30 m would crack after drilling,for the magnitudes of 3σh-σHis low to-9 MPa,about the tensile strength of surrounding rocks.

One principal stress is nearly along the vertical direction in every case presented in Table 5;therefore,the hydraulic fracturing method might be used in these situations,but breakdown pressurePbshould be lower than the shut-in pressure,i.e.the minor principal stressσh.In other words,Pbwould not be the peak value in the frst cycle,but the point where the slope of pressure-time curve begins to decline.

6.Conclusions

None of strength criteria,of which the parameters are determined from conventional triaxial compression strengths,might present reasonable tensile strength for all rocks.Tensile strength of rock is an independent parameter to be determined from test.

The generalized H-B criterion usually presents a tensile strength lower than the measured magnitude.However,the exponential criterion predicts well tensile strengths for granites, but overestimates for other rocks;therefore,the criterion may be extended to tensile-compressive stresses with the tangent line combined a tension cut-off,and applicable to rock engineering, such as the estimation of in-situ stress with hydraulic fracturing.

Breakdown pressure may be lower than the shut-in pressure in some cases;and it is not the peak value in the frst cycle,but the point where the slope of pressure-time curve begins to decline.

Confict of interest

The author wishes to confrm that there are no known conficts of interest associated with this publication and there has been no signifcant fnancial support for this work that could have infuenced its outcome.

Acknowledgments

The author would like to acknowledge the reviewers for their valuable comments and suggestions,and thanks to Reviewer#1 for his reminding the initial proposer of the fractional criterion.

Anderson C,Christianson R.Variability of hydraulic fracturing rock stress measurements and comparison of triaxial overcoring results made in the same borehole.In:Rock stress.Rotterdam:A.A.Balkema;2003.p.315-20.

Bineshian H.Verifcation of the applicability of rock failure criteria in relation to the limestone of Iran and suggestion of a suitable failure criterion.MS Thesis. Tehran,Iran:Tarbiat Modares University;2000.

Bineshian H,Ghazvinian A,Bineshian Z.Comprehensive compressive-tensile strength criterion for intact rock.Journal of Rock Mechanics and Geotechnical Engineering 2012;4(2):140-8.

Cai M.Practical estimates of tensile strength and Hoek-Brown strength parametermiof brittle rocks.Rock Mechanics and Rock Engineering 2010;43(2):167-84.

Cai MF,Liu WD,Li Y.In-situ stress measurement at deep position of Linglong Gold Mine and distribution law of in-situ stress feld in mine area.Chinese Journal of Rock Mechanics and Engineering 2010;29(2):227-33(in Chinese).

Carter BJ,Duncan SEJ,Lajtai EZ.Fitting strength criteria to intact rock.Geotechnical and Geological Engineering 1991;9(1):73-81.

Chen QC,Mao JZ,Hou YH.Study on infuence of topography on in-situ stress by interpretation of measurement data of in-situ stress.Chinese Journal of Rock Mechanics and Engineering 2004;23(23):3990-5.

Eberhardt E.ISRM suggested method:the Hoek-Brown failure criterion.Rock Mechanics and Rock Engineering 2012;45(6):981-8.

Efmov VP.The rock strength in different tension conditions.Journal of Mining Science 2009;45(6):569-75.

Fairhurst C.On the validity of the“Brazilian”test for the brittle materials.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1964;1(4):535-46.

Ghazvinian AH,Fathi A,Moradian ZA.Failure behavior of marlstone under triaxial compression.International Journal of Rock Mechanics and Mining Sciences 2008;45(5):807-14.

Haimson B,Chang C.A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of westerly granite.International Journal of Rock Mechanics and Mining Sciences 2000;37(3):285-96.

Haimson BC,Cornet FH.ISRM suggested methods for rock stress estimation-Part 3:hydraulic fracturing(HF)and/or hydraulic testing of pre-existing fractures (HTPF).InternationalJournalofRockMechanicsandMiningSciences 2003;40(6):1011-20.

Hobbs DW.The strength and stress-strain characteristics of coal in triaxial compression.Journal of Geology 1964;72(2):214-31.

Hoek E,Wood D,Shah S.A modifed Hoek-Brown criterion for jointed rock masses. In:Proceedings of the Rock Characterization Symposium of ISRM:Eurock 92. London,UK:British Geotechnical Society;1992.p.209-24.

Hoek E,Brown ET.Underground excavation of rock.London,UK:Institution of Mining and Metallurgy;1980.

Hudson JA,Brown ET,Rummel F.The controlled failure of rock discs and rings loaded in diametral compression.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1972;9(2):241-8.

Jaeger JC,Cook NGW,Zimmerman RW.Fundamentals of rock mechanics.New York, USA:Wiley-Blackwell;2007.

Kang HP,Lin J,Hang X.Research and application of in-situ stress measurement in deep mines.Chinese Journal of Rock Mechanics and Engineering 2007;26(5): 929-33(in Chinese).

Mogi K.Experimental rock mechanics.London,UK:Taylor and Francis;2007.

Murrell SAF.The effect of triaxial stress systems on the strength of rock at atmospherictemperatures.GeophysicalJournalRoyalAstronomicalSociety 1965;10(3):231-81.

Pine RJ,Tunbridge LW,Kwakwa K.In-situ stress measurement in the Carnmenellis granite.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 1983;20(2):51-62.

Rafai H.New empirical polyaxial criterion for rock strength.International Journal of Rock Mechanics and Mining Sciences 2011;48(5):922-31.

Ramsey JM,Chester MF.Hybrid fracture and the transition from extension fracture to shear fracture.Nature 2004;428(1):63-6.

Schwartz AE.Failure of rock in the triaxial shear test.In:Proceedings of the 6th US Symposium on Rock Mechanics,Rolla,Missouri,USA;1964.p.109-51.

Sheorey PR,Ak Biswas,Choubey VD.An empirical failure criterion for rocks and jointed rock masses.Engineering Geology 1989;26(2):141-59.

Sriapai T.True triaxial compressive strengths of Maha Sarakham rock salt.MS Thesis. Nakhon Ratchasima,Thailand:Suranaree University of Technology;2010.

Tan CX,Shi L,Sun WF,Lei WZ,Sun Y,Wang RJ,Wu SR.Research on tectonic stress plane.Chinese Journal of Rock Mechanics and Engineering 2004;23(23):3970-8 (in Chinese).

Von Kármán T.Festigkeitsversuche unter all seitigem Druck.Z Verein Deut Ingr 1911;55:1749-59.

You MQ.True-triaxial strength criteria for rock.International Journal of Rock Mechanics and Mining Sciences 2009;46(1):115-27.

You MQ.Mechanical characteristics of the exponential strength criterion under conventional triaxial stresses.International Journal of Rock Mechanics and Mining Sciences 2010a;47(2):195-204.

You MQ.Comparison of the accuracy of some conventional triaxial strength criteria for intact rock.International Journal of Rock Mechanics and Mining Sciences 2011;48(5):852-63.

You MQ.Comparison of two true-triaxial strength criteria.International Journal of Rock Mechanics and Mining Sciences 2012;54:114-24.

You MQ.Study of deformation and failure of rock based on properties of cohesion and friction.Journal of Geomechanics 2005a;11(3):286-95(in Chinese).

You MQ.Study on the geo-stresses measurement with hydro-fracture of borehole. Chinese Journal of Geotechnical Engineering 2005b;27(3):350-3(in Chinese).

You MQ.Strength and failure of rock due to hydraulic fracture.In:Rock stress and earthquake.London,UK:Taylor and Francis;2010b.p.185-8.

You MQ,Su CD,Chen XL.Brazilian splitting strengths of discs and rings of rocks in dry and saturated conditions.Chinese Journal of Rock Mechanics and Engineering 2011;30(3):464-72(in Chinese).

You MQ,Zhou ST,Su CD.Direct tensile experiment of rock specimens under confning pressure.Journal of Henan Polytechnic University 2006;25(4):255-61(in Chinese).

Yu MH.Advances in strength theories for materials under complex stress state in the 20th Century.Applied Mechanics Review 2002;55(2):169-218.

Yu Y,Zhang J,Zhang J.A modifed Brazilian disk tension test.International Journal of Rock Mechanics and Mining Sciences 2009;46(3):421-5.

Mingqing Youobtained his B.Sc.from Fudan University, Shanghai,and M.Sc.and Ph.D.degrees from China University of Mining and Technology,Xuzhou,China.He is now a professor of Henan Polytechnic University.He has been involved in mechanical and geotechnical research and education for nearly 30 years.He is the author or coauthor of more than 100 scientifc papers and he serves in the Editorial BoardofChinese Journal of RockMechanics and Engineering.

*Tel.:+86 391 3988278.

E-mail addresses:youmq@hpu.edu.cn,youmq640930@aliyun.com.

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2015.05.002