A theoretical derivation of the Hoek-Brown failure criterion for rock materials

Jinping Zuo,Huihi Liu,Hongto Li

aState Key Laboratory of Coal Resources and Safe Mining,China University of Mining and Technology,Beijing 100083,China

bInstitute of Rock Mechanics and Fractals,School of Mechanics and Civil Engineering,China University of Mining and Technology,Beijing 100083,China

cAramco Research Center,Houston,TX 77084,USA

A theoretical derivation of the Hoek-Brown failure criterion for rock materials

Jianping Zuoa,b,*,Huihai Liuc,Hongtao Lia

aState Key Laboratory of Coal Resources and Safe Mining,China University of Mining and Technology,Beijing 100083,China

bInstitute of Rock Mechanics and Fractals,School of Mechanics and Civil Engineering,China University of Mining and Technology,Beijing 100083,China

cAramco Research Center,Houston,TX 77084,USA

A R T I C L E I N F O

Article history:

Received 7 March 2015

Received in revised form

18 March 2015

Accepted 20 March 2015

Available online 7 April 2015

Failure criterion

Triaxial compression

Micro-failure orientation

Fracture mechanics

Brittle-ductile transition

This study uses a three-dimensional crack model to theoretically derive the Hoek-Brown rock failure criterion based on the linear elastic fracture theory.Specifcally,we argue that a failure characteristic factor needs to exceed a critical value when macro-failure occurs.This factor is a product of the microfailure orientation angle(characterizing the density and orientation of damaged micro-cracks)and the changing rate of the angle with respect to the major principal stress(characterizing the microscopic stability of damaged cracks).We further demonstrate that the factor mathematically leads to the empirical Hoek-Brown rock failure criterion.Thus,the proposed factor is able to successfully relate the evolution of microscopic damaged crack characteristics to macro-failure.Based on this theoretical development,we also propose a quantitative relationship between the brittle-ductile transition point and confning pressure,which is consistent with experimental observations.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

The strength theory of brittle materials,such as rock and concrete,has been a subject of intensive study for many years,because the failure of brittle material is of great concern in designing and evaluating the safety and stability of engineering structures and geological engineering facilities.Consequently,the failure criterion for brittle material has become one of the most important subjects in many areas(Yu,2004;Paterson and Wong,2005;Jaeger et al., 2007;Zuo et al.,2008).

Griffth(1921)frst postulated that the fracture of brittle materials occurs when the energy-release rate during crack growth exceeds the rate that energy is required.Griffth’s theory,which indicates that micro-cracks are a major cause of failure of materials (Griffth,1921,1924),has been extended for a biaxially stressed body with randomly oriented cracks(Odé,1960).A macro-failure criterion,generally known as the Griffth’s criterion,is expressed in terms of the biaxial principal stressesσ1,σ2and the magnitude of the uniaxial tensile strengthT0,i.e.（σ1-σ2）2-8T0（σ1+σ2）=0 forσ1＞-3σ2andσ2=T0forσ1＜-3σ2.While Griffth’s criterion predicts that uniaxial compressive strengthσcis about eight times the uniaxial tensile strengthσt,most experimental results show that values forσc/σtare larger than 10,even up to 50.

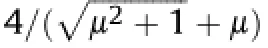
Murrell(1965)suggested that the biaxial criterion could be generalizedfortriaxialstressasaparaboloid:（σ2-σ3）2+（σ3-σ1）2+（σ1-σ2）2-24T0（σ1+σ2+σ3）=0.Under the uniaxial compression conditions forσ2=σ3=0 andσc=σ1,it can predict thatσc/σt=12.However,there seems to be no a priori reason for selecting this triaxial criterion except on empirical grounds.Based on a micro-mechanical analysis of sliding cracks, Wiebols and Cook(1968)proposed a new criterion.However,their theory suggests that with respect to polyaxial compression,the intermediate principal stress has a pronounced and predictable effect,which may not always be considered in the existing theories.

The classic Hoek-Brown failure criterion,empirical in its formulation and based on numerous experimental data,has been widely used to predict the failure of rocks(Hoek and Brown,1980a, b).While the criterion has been modifed or extended for a number of felds,linkage between this well-known criterion and the micromechanical mechanisms of sliding cracks is still rare in the literature(Hoek,1983,1998;Hoek and Brown,1997),providing such a linkage would have signifcant implications for improving our understanding of rock damage/failure processes.

The major objective of this study is to make an effort to establish the linkage mentioned above,based on a recent study in which Zuo et al.(2008)have derived a theoretical nonlinear strength criterion for rock-like material based on fracture mechanics,a criterion with a similar mathematical expression to the Hoek-Brown criterion. Hoek and Martin(2014)recentlycompared our theoretical criterion with Mohr-Coulomb and Griffth’s criterion in Fig.3 of their paper. This study is an effort to extend the work of Zuo et al.(2008)by including additional insights and analyses.The most important issue in Zuo et al.(2008)is how to choose the failure characteristic factor that relates the micro-mechanism to macro-failure,and our study provides more physical justifcations for the chosen factor. Also,the study of Zuo et al.(2008)was based on a two-dimensional model for an initial sliding crack,while in this study we focus on three-dimensional(3D)cases.In addition,we discuss how to interpret the brittle-ductile transition phenomenon in rocks.

2.Fundamental hypothesis and model

There is abundant evidence for the existence of Griffth cracks or other crack-like faws in brittle materials(Griffth,1921,1924;Peng and Johnson,1972;Schovanec,1986;Mura,1987;Vardoulakis and Papamichos,1991).In addition,the low strength of some brittle materials results mainly from the presence of these micro-cracks or faws.In the present work,we assume that numerous Griffth micro-cracks are randomly distributed in rocks.A model of frictional sliding cracks has been discussed in the literature(Cook, 1965;Holcomb,1978;Kachanov,1982a,b;Li and Yang,2006). Although the crack interactions can be taken into account by modifcations of a self-consistent method,in this paper,these micro-crack interactions are neglected,so that traction on crack faces can be calculated as being induced by external load.In this way,a simplifed model for a sliding,disk-shaped,closed crack of diameter 2ain an infnite plate can be generated,as shown in Fig.1. We adopt the convention common in geologic and rock mechanics literature that compressive stress is positive and tensile stress is negative,and designate the major,intermediate,and minor principal stresses asσ1,σ2,σ3,respectively,where the three subscripts representthe coordinateaxesx1,x2,x3,respectively.The orientation of a disk-shaped crack can be defned bydirection cosinesl,m,n.If a unique sphere is built up with the following equation:

then the orientation of the crack plane is determined by the normal direction of pointM.The normal stressσnand shear stress τncomponents on the disk-shaped crack can be given in terms of the three principal stresses,and as a function of the direction cosinesl,m,n:

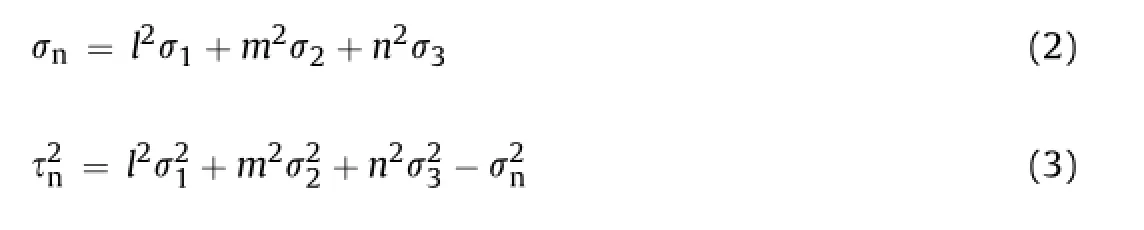
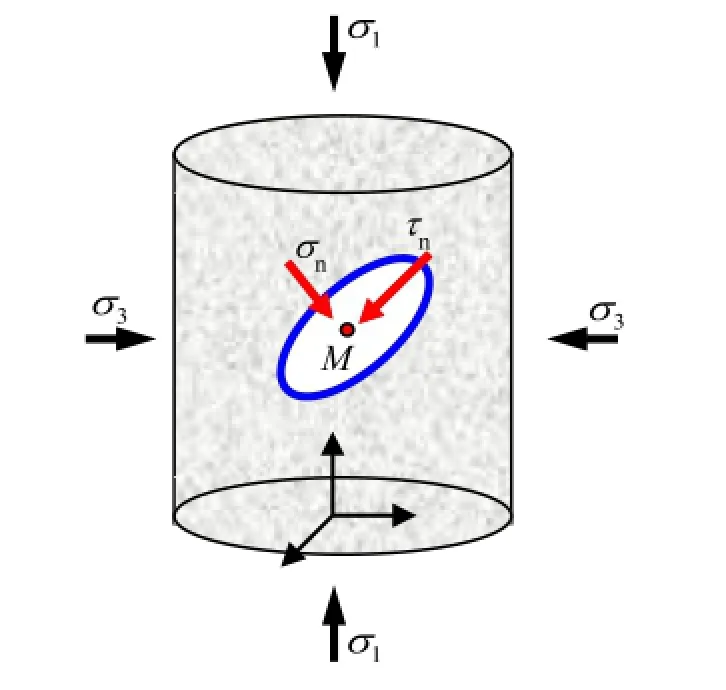
Fig.1.A disk-shaped crack of diameter 2ain an infnite plate under triaxial compression.

3.Propagation conditions for a disk-shaped crack

Although inelastic effects are involved at crack tips in various rocks(Hoagland et al.,1973),and even elastic behavior in the most highly stressed regions may be nonlinear,the practical analysis of the stress distribution in the neighborhood of the crack tip is usually based on the classical linear theory of elasticity.Therefore, according to linear elastic fracture mechanics(Anderson,2005),the crack mode in Fig.1 is in-plane shear(Mode II),a mode corresponding to in-plane shear loading that tends to slide one crack face with respect to the other.The stress intensity factor depends on both shear stressτnand friction stressτμ,which is parallel to the crack plane.According to Amontons’law,τμ=μσn,whereμandσnare the friction coeffcient for the pre-existing sliding crack surface and the normal stress acting on the disk plane,respectively.It is obvious thatτμis a key factor in suppressing crack propagation.The effective shear stressτecan be expressed as

For the 3D problem,the effective shear stressτeinitiates frictional sliding.In addition,ifτeis suffciently high to overcome the frictional resistance along the initial crack,frictional slip results in tensile stress concentrations at the two tips of the sliding crack, which,in turn,may induce nucleation of“wing cracks”(Kachanov, 1982a).Prior tothe onsetof crack propagation,the maximum stress intensity factorKIImaxof mode II at the initial crack tip approximately is

whereνis the Poisson’s ratio.

If the wing crack length is infnitesimal,the propagation conditions for a disk-shaped crack under triaxial compression,based on the mixed fracture criterion,can be expressed as(Kachanov, 1982b;Cotterell and Rice,1980):

Because thewing crack is caused by the local tensile stress at the disk-shaped crack tip,the fracture toughnessKIccan be calculated as

whereσtis the local tensile strength at the tip of the disk-shaped crack.Substituting Eqs.(5)and(7)into Eq.(6),we then get:

Usingβto denote（1-ν/2）κ,Eq.(8)can then be rewritten as

4.The attitude angle parameterφto characterize microfailure orientation

Assume there is a sphere with a unit length radius,with the coordinate originOas the center of the sphere.Based on the geometric symmetry of sphere,one can concentrate on the eight equal parts in the sphere,as shown in Fig.2.Since there are numerous Griffth micro-cracks distributed randomly in rock materials,we assume that all these cracks will converge.Assuming the movement of one endpoint of any disk-shaped crack to the coordinate originO,there develops an intersection point between the normal line of any cracks between the normal line of any cracks and the surface of the upper hemisphere.Fornrock samples under triaxial compression,all intersection points can make up an intersection region that depends on the three principal stresses.Although evidence has shown thatσ2does infuence the failure of rock(Al-Ajmi and Zimmerman,2005),the shape of the intersection region is rather complicated under true triaxial compression(σ1＞σ2＞σ3). Therefore,we discuss only the special case ofσ1＞σ2=σ3.According to the axial symmetry,these intersection points will make up a band region located on two latitude linesABandCD(the shadow region in Fig.2).An angleθis used to denote the“microfailure orientation angle”under triaxial compression.The angleθ corresponds to the angleαin Zuo et al.(2008),and they have the same physical meaning,i.e.“micro-failure orientation angle”. Whenσ2=σ3,Eq.(2)becomes the following form derived from Eq. (1)and cosθ=l:

Then,Eq.(3)can be further simplifed as

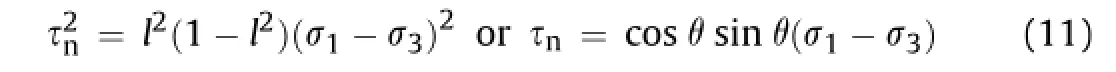
From Eqs.(4)and(9)-(11),we can get

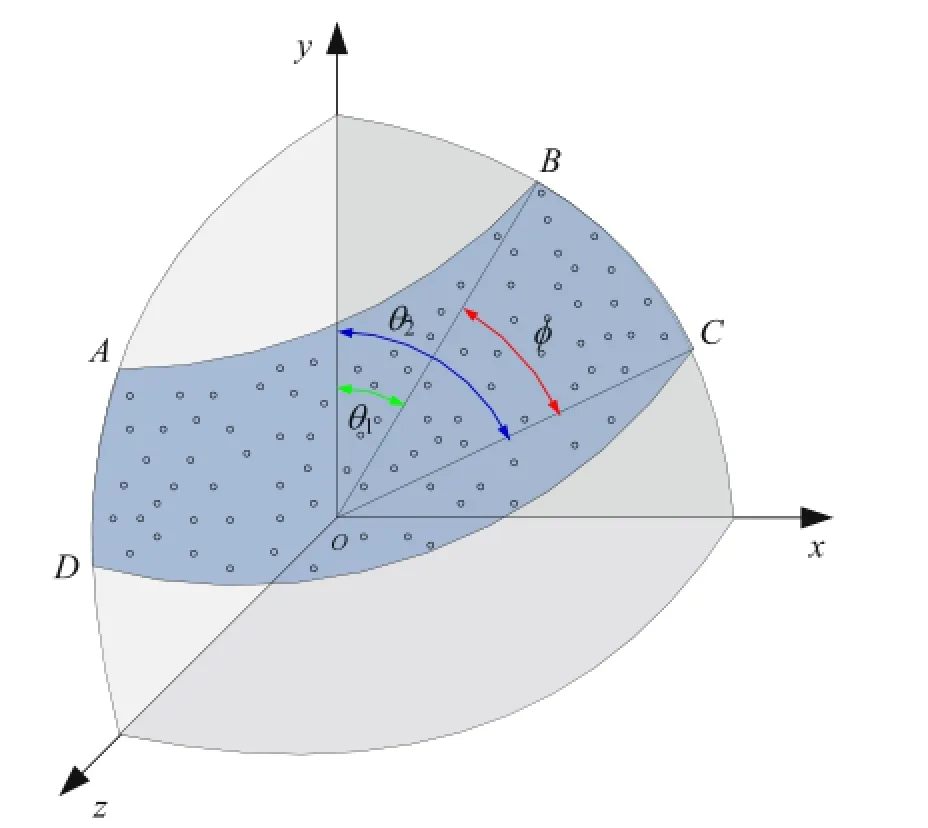
Fig.2.The band region of intersecting point between the normal line of any microcracks and unit sphere.

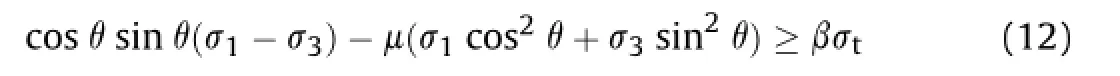
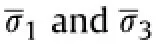
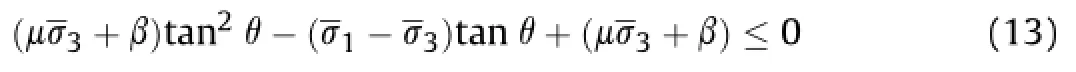
Then,we have

where

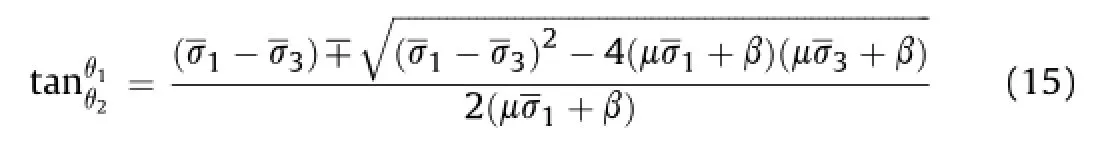
An attitude angle can be defned,i.e.φ=θ2-θ1,then we have

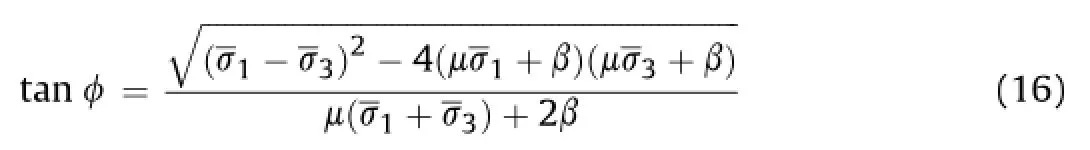
Eq.(16)gives the relationship between attitude angleφand external load.In addition,the range of the attitude angleφis from 0 toπ/2.

5.The failure characteristic factor for rocks and derivation of the Hoek-Brown criterion

Rock failure processes can be approximately described as follows.There are various pre-existing micro-cracks in rock materials that are potentially of vital signifcance to their brittle behavior. When the external load achieves a critical value,pre-existing(and some new)micro-cracks will initiate and propagate.These microcracks will tend not to propagate in their own planes,but rather swing into an orientation more nearly parallel to the orientation of the major principal stressσ1(Diederichs,2003).With a further increase in external load,some subcritical micro-cracks will initiate,propagate,and tend to become unstable.When numerous micro-failures approach a critical condition,a macro-failure will occur,and the rock will then be broken.By contrast,micro-failures are usually constrained by the confning pressureσ3;thus,the higher the confning pressure,the smaller the micro-failure.

In Section 3,we obtained an expression for the portion of microcracks that are subjected to micro-damage.The key issue is how to relate this damage to macro-failures.The latter is determined by two microscopic variables.The frst variable is the attitude angle,φ. Obviously,a largerφcorresponds to a larger relative portion of damaged internal micro-cracks,and thus to a larger possibility for macro-failure.

From Eq.(16),we have

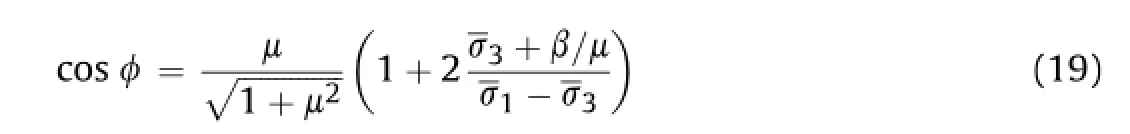
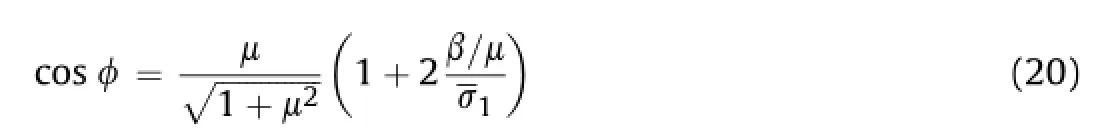
Substituting Eq.(19)into Eq.(18)yields

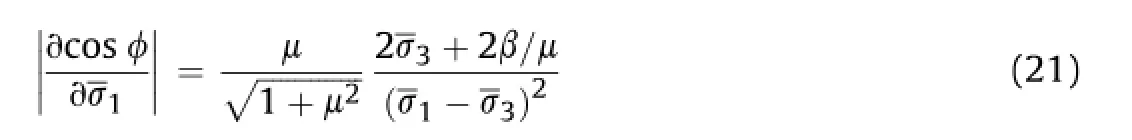
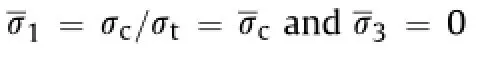
Consequently,the critical value forFis the right part of Eq.(22). Substituting this value into Eq.(21),we have

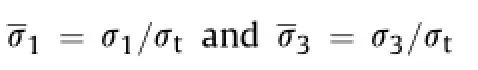
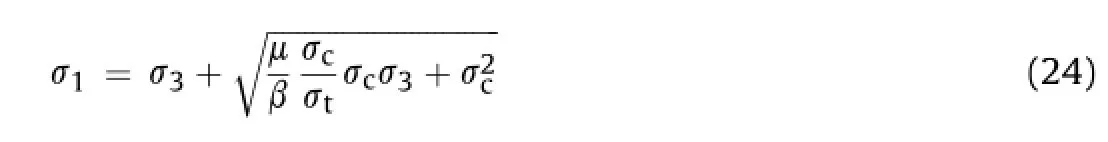
whereμis about 0.2-0.8(Paterson and Wong,2005).The parametersμ,β,σt,σcdepend on rock properties,and all can be obtained from experimental data.

The original Hoek-Brown empirical criterion is(Hoek and Brown,1980a,b):

wheremandsare the material parameters for the rock.Withs=1 for intact rock,Eq.(25)becomes

Thus,Eq.(24)is the same as Eq.(26)form=μσc/(βσt).In other words,weare able toderive the Hoek-Brown criterion frommicromechanical considerations,based on the failure characteristic factor defned in Eq.(17).This fact in itself strongly supports the reasonableness and usefulness of our failure characteristic factor. While it is beyond the scope of this study,we speculate that this factor could be used as a damage variable in damage mechanics studies,because it is more or less equivalent to the Hoek-Brown criterion,as we have demonstrated here.Note that how to choose the damage variable is at present a key issue in the damage mechanics community.

6.The micro-mechanisms of brittle-ductile transitions

It is usually accepted that material failure is brittle type if no apparent plastic deformation takes place before fracturing.In ductile failure,by contrast,extensive plastic deformation takes place.Experimental results indicate that while most rocks exhibit brittleness under atmospheric pressure,ductility in rock can also be achieved in the laboratory with the aid of suffciently high confning pressures and temperatures(Paterson and Wong,2005; Jaeger et al.,2007).In other words,there exists a critical condition for the transition from brittleness to ductility.In this paper,we concern with the effects of confning pressure.The brittle-ductile transition occurs when the external confning pressure reaches a critical value.The state in which this change happens is called a brittle-ductile transition state.In addition,the investigation of the brittle-ductile transition has become very important in many geologic situations,and may also have relevance to some engineering applications.

Studies of brittle-ductile transition phenomena have been reported by a number of researchers(Paterson and Wong,2005; Jaeger et al.,2007).However,most of these studies are from a macroscopic or phenomenological point of view,and take no accountofthemicro-mechanisms,especiallythemicro-crack mechanisms under high confning pressure.For example,some investigators artifcially defne the failure of rock as brittle type(or ductile type)if the value of strain or confning pressure of failure is less than(or larger than)a specifc value.For example,the strain value of 3%-5%corresponding to failure is often taken for defning the brittle-ductile transition(Heard,1960;Evans et al.,1990).Some investigators have proposed that,as a general rule,the brittleductile transition should be related to the strength of rocks(Mogi, 2005).For instance,in silicate rocks under compression,it occurs when the confning pressure is equal to roughly 1/3 the stress difference at failure;in carbonate rocks,at about 1/4 the stress difference.The ductility of rock in extension requires much higher confning pressures(Heard,1960).However,in the case of porous sandstone,the transition to ductility occurs at an effective confning pressure of about 0.15 times the critical effective pressure for the onset of grain crushing under hydrostatic pressure(Wong et al.,1997).In other words,there is no strict or unifed standard from which to choose the critical parameter for the brittle-ductile transition.Parameter selection varies with individual investigator or rock types,indicating the diffculty in making clear and strict defnitions of the brittle-ductile transition point on a macroscale. Therefore,it is necessary to revisit the concepts of brittle,ductile, and brittle-ductile transition states for the micro/mesoscale.This section provides some new information on the subject.

In light of the previous derivation of the strength criterion,we defne the brittle-ductile transition as occurring in rock when the confning pressure achieves a suitable value.That value is achieved when the micro-failure in rock is completely restrained.This is a defnition of the rock brittle-ductile transition point at the micro/ mesoscale.Since there is clearly a causal relationship between micro-failure and rock dilatancy,this defnition is entirely equivalent to the macro-defnition.

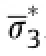
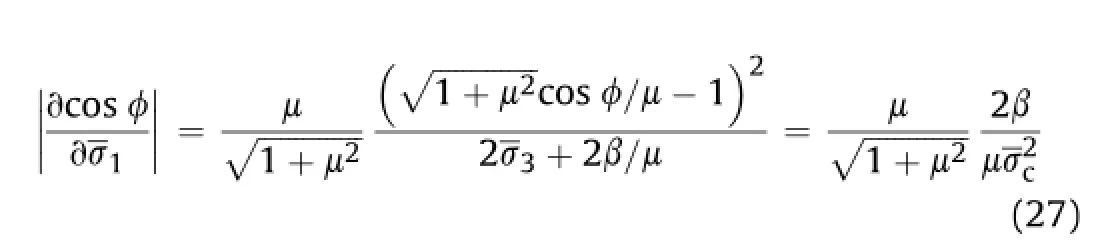
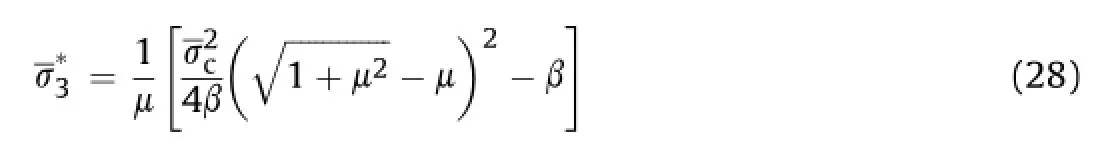
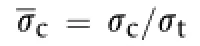
An empirical failure criterion has also been proposed in Wong et al.(1997),indicating that for most rocks,the confning pressure must always be smaller than the uniaxial compressive strength to maintain rock brittle behavior:

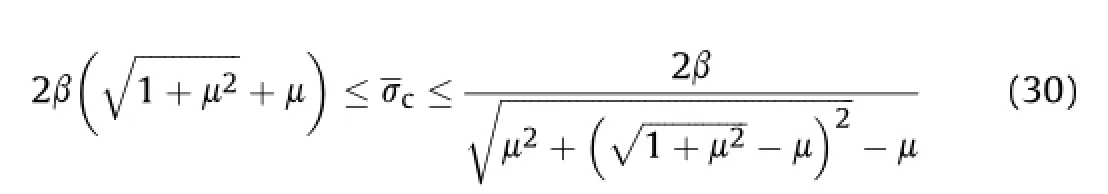
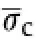
Eq.(31)indicates that(the ratio of rock uniaxial compressive strengthσcto uniaxial tensile strengthσt)is an important parameter for evaluating rock brittleness.The greater this ratio,the more brittle the rock,and vice versa.

7.Conclusions

A 3D crack model is employed to theoretically derive the Hoek-Brown rock failure criterion based on the linear elastic fracture theory.Specifcally,we argue that our proposed failure characteristic factor needs to exceed a critical value when macro-failure occurs.This factor is a product of a micro-failure orientation angle(characterizing the density and orientation of damaged micro-cracks)and the changing rate of the anglewith respect tothe major principal stress(characterizing the microscopic stability of damaged cracks).We further demonstrate that the factor mathematically leads to the empirical Hoek-Brown rock failure criterion. One important implication of the study is that the proposed factoris able to relate the evolution of microscopic damaged-crack characteristics to macro-failure.

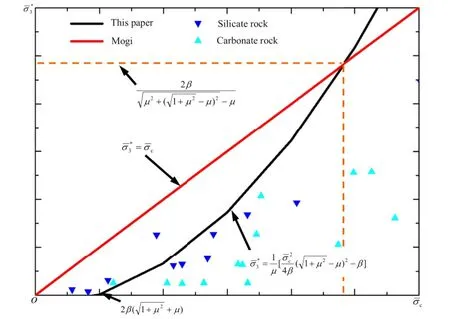
Fig.3.The relationship between the confning pressureat brittleness-ductility transition and the value ofσc/σt.

Based on our theoretical development,this paper also gives a clear interpretation of the brittleness and ductility of rock on the microscale.A quantitative relationship between the brittle-ductile transition point and confning pressure is derived and shown to be consistent with experimental observations.

Confict of interest

The authors wish to confrm that there are no known conficts of interest associated with this publication and there has been no signifcant fnancial support for this work that could have infuenced its outcome.

Acknowledgments

This work is supported by the National Natural Science Foundation of China(No.51374215),Fok Ying Tung Education Foundation(No.142018),Beijing Major Scientifc and Technological Achievements into Ground Cultivation Project and the 111 Project (No.B14006).The second author(Huihai Liu)thanks the management of Aramco Research Center for approving publication of the work.Also,the authors would like to acknowledge the anonymous reviewers for their valuable comments and suggestions,which helped to signifcantly improve the quality of this paper.

Al-Ajmi AM,Zimmerman RW.Relation between the Mogi and the Coulomb failure criteria.InternationalJournalofRockMechanicsandMiningSciences 2005;42(3):431-9.

Anderson TL.Fracture mechanics:fundamentals and applications.Boca Raton,FL, USA:Taylor&Francis;2005.

Cook NGW.The failure of rock.International Journal of Rock Mechanics and Mining Sciences 1965;2(4):389-403.

Cotterell B,Rice JR.Slightly curved or kinked cracks.International Journal of Fracture 1980;16(2):155-69.

Diederichs MS.Rock fracture and collapse under low confnement conditions.Rock Mechanics and Rock Engineering 2003;36(5):339-81.

Erdogan F,Sih GC.On the crack extension in plates under plane loading and transverse shear.Journal of Fluids Engineering 1963;85(4):519-25.

Evans B,Frederich JT,Wong TF.The brittle-ductile transition in rocks:recent experimental and theoretical progress.In:Duba AG,Durham WB,Handin JW, Wang HF,editors.The brittle-ductile transition in rocks.Washington DC,USA: American Geophysical Union;1990.p.1-20.

Griffth AA.The phenomena of rupture and fow in solids.Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences 1921;221:163-98.

Griffth AA.The theory of rupture.In:Biezeno CG,Burgers JM,editors.Proceedings of the 1st International Congress for Applied Mechanics.Delft,Netherlands: Waltman;1924.p.54-63.

Heard HC.Transition from brittle fracture to ductile fow in Solenhofen limestone as a function of temperature,confning pressure,and interstitial fuid pressure.In: Griggs D,Handin J,editors.Rock deformation.Boulder,Colorado,USA: Geological Society of America;1960.p.193-226.

Hoagland RG,Hahn GT,Rosenfeld AR.Infuence of microstructure on fracture propagation in rock.Rock Mechanics 1973;5(2):77-106.

Hoek E,Brown ET.Empirical strength criterion for rock mass.Journal of Geotechnical and Geoenvironmental Engineering 1980a;106(9):1013-35.

Hoek E,Brown ET.Underground excavations in rock.London,UK:Institution of Mining and Metallurgy;1980b.

Hoek E.Strength of jointed rock masses.Géotechnique 1983;23(3):187-223.

Hoek E,Brown ET.Practical estimates of rock mass strength.International Journal of Rock Mechanics and Mining Sciences 1997;34(8):1165-86.

Hoek E,Martin CD.Fracture initiation and propagation in intact rock-a review. Journal of Rock Mechanics and Geotechnical Engineering 2014;6(4):287-300.

Hoek E.Reliability of Hoek-Brown estimates of rock mass properties and their impact on design.International Journal of Rock Mechanics and Mining Sciences 1998;35(1):63-8.

Holcomb DJ.A quantitative model of dilatancy in dry rock and its application to Westerly granite.Journal of Geophysical Research 1978;83(B10):4941-50.

Jaeger JC,Cook NGW,Zimmerman RW.Fundamentals of rock mechanics.4th ed. Oxford,UK:Blackwell;2007.

Kachanov ML.A microcrack model of rock inelasticity,part I:frictional sliding on microcracks.Mechanics of Materials 1982a;1(1):19-27.

Kachanov ML.A microcrack model of rock inelasticity,part II:propagation of microcracks.Mechanics of Materials 1982b;1(1):29-41.

Li YP,Yang CH.On sliding crack model for brittle solids.International Journal of Fracture 2006;142(3-4):323-30.

McLintock FA,Walsh JB.Friction on Griffth cracks in rocks under pressure.In: Proceedings of the 4th U.S.National Congress of Applied Mechanics,Berkeley, California,vol.II;1962.p.1015-21.

Mogi K.Experimental rock mechanics.London,UK:Taylor&Francis;2005.

Mura T.Micromechanics of defects in solids.Dordrecht,Netherlands:Kluwer Academic Publishers;1987.

Murrell SAF.The effect of triaxial stress systems on the strength of rocks at atmospheric temperatures.Geophysical Journal of the Royal Astronomical Society 1965;10(3):231-81.

Nuismer RJ.An energy release rate criterion for mixed mode fracture.International Journal of Fracture 1975;11(2):245-50.

Odé H.Faulting as a velocity discontinuity in plastic deformation.In:Griggs D, Handin J,editors.Rock deformation.Boulder,Colorado,USA:Geological Society of America;1960.p.293-321.

Paterson MS,Wong TF.Experimental rock deformation-the brittle feld.Berlin, Germany:Springer;2005.

Peng S,Johnson AM.Crack growth and faulting in cylindrical specimens of Chelmsford granite.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1972;9(1):37-86.

Schovanec LA.Griffth crack problem for an inhomogeneous elastic material.Acta Mechanica 1986;58(1-2):67-80.

Sih GC,Macdonald B.Fracture mechanics applied to engineering problems-strain energy density fracture criterion.Engineering Fracture Mechanics 1974;6(2): 361-86.

Sih GC.Strain-energy-density factor applied to mixed mode crack problems.International Journal of Fracture 1974;10(3):305-21.

Vardoulakis I,Papamichos E.Surface instabilities in elastic anisotropic media with surface-parallel Griffth cracks.International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts 1991;28(2-3):163-73.

Wiebols GA,Cook NGW.An energy criterion for the strength of rock in polyaxial compression.International Journal of Rock Mechanics and Mining Sciences& Geomechanics Abstracts 1968;5(6):529-49.

Wong TF,David C,Zhu W.The transition from brittle faulting to cataclastic fow in porous sandstones:mechanical deformation.Journal of Geophysical Research 1997;102(B2):3009-25.

Yu MH.Unifed strength theory and its applications.Berlin,Germany:Springer; 2004.

Zuo JP,Li HT,Xie HP,Ju Y,Peng SP.A nonlinear strength criterion for rocklike materials based on fracture mechanics.International Journal of Rock Mechanics and Mining Sciences 2008;45(4):594-9.

Jianping Zuoobtained his M.Sc.and Ph.D.from China University of Mining and Technology(Beijing),China.He is professor of Engineering Mechanics at the China University of Mining and Technology(Beijing)where he has been Head of the Department of Engineering Mechanics,School of Mechanics and Civil Engineering.He has been involved in rock mechanics and mining engineering research, consulting and teaching for more than 10 years.He is in charge of and/or participates in 12 scientifc research projects,which were funded by National Natural Science Foundation of China,National Basic Research Program of China(973 Program),Beijing Major Scientifc and Technological Achievements into Ground Cultivation Project, the 111 Project and Coal Mines Corporations.He is the author or co-author of more than 90 scientifc papers.He has received 3 national patents,and 2 Natural Science and Technology Progress Awards.In recent years,he has been awarded National Excellent Doctoral Dissertation Award(2009),New Century Excellent Talents of the Ministry of Education(2009),Coal Youth Science and Technology Award in China(2010),Beijing Outstanding Young Talent(2014),Fok Excellent Young Teachers Award(2014).

*Corresponding author.Tel.:+86 10 62331358.

E-mail address:zjp@cumtb.edu.cn(J.Zuo).

Peer review under responsibility of Institute of Rock and Soil Mechanics, Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2015.03.008