Analysis of horizontal displacement distribution caused by single advancing longwall panel excavation

K.Tajduˊs

Strata Mechanics Research Institute,Polish Academy of Sciences,Krakow,Poland

Analysis of horizontal displacement distribution caused by single advancing longwall panel excavation

K.Tajduˊs*

Strata Mechanics Research Institute,Polish Academy of Sciences,Krakow,Poland

A R T I C L E I N F O

Article history:

Received 2 January 2015

Received in revised form

16 March 2015

Accepted 17 March 2015

Available online 8 May 2015

Horizontal displacements/movements

Surface deformations

Mining exploitation

Horizontal displacement coeffcient

Center of gravitation(COG)zone

The paper presents an analysis of the horizontal displacement of surfaces induced by exploitation in a longwall panel.The panel under discussion is No.698 of Prosper Haniel coal mine,Germany.The author discusses both the distribution of displacement vectors,according to the theory assuming surface point displacement towards the center of gravitation(COG)zone of a selected deposit element,and the analysis of horizontal displacement measurements,based on the assumption that the value of horizontal displacement is proportional to the slope of the subsidence trough.Finally,the value of horizontal displacement coeffcientBis estimated for particular longitudinal and transverse measurement section of the analyzed longwall No.698.

©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

Underground longwall excavation creates deformations inside the rock mass which can appear on the surface.One indicator of such a deformation is the vector of rock mass movement,which can be easily divided into two components:vertical and horizontal movements.In the past,many scientists have dealt with the problem of vertical movement(subsidence)determination.Due to the subsidence of rock mass caused by underground mining,such operations have been observed and quantifed since early 20th century.Work on subsidence calculation methods was started by Schmitz(Lehmann et al.,1942).Later,Awierszyn(1947)proposed a methodology assuming the kinetics of the rock displacement process in analytical solutions,which allowed for the introduction of universal theoretical descriptions of rock mass movement.The above proposal gave rise to the intensive development of calculation methods,especially methods based on the normal distribution of mining infuence,like Knothe’s method(Knothe,1953,1984; Sroka et al.,2011)and Ruhrkohle method(Sroka,2010;Sroka et al.,2011).

But in spite of the many theories and methods used to calculate surface deformations above underground operations,inter alia, Keinhorst(1925),Sann(Lehmann et al.,1942),Bals(1931/1932), Knothe(1953),NCB(1975),etc.,estimations of the values and distribution of horizontal movement are still unclear.

This paper presents the monitoring and analysis of horizontal movements caused by a single longwall panel excavation,No.698. Analysiswas carried out based on two the most popularhypotheses of horizontal movements:

(1)Theories assuming the displacement of surface points towards the center of gravitation(COG)of a selected element of deposit, e.g.the theories of:Keinhorst(1925),Bals(1931/1932), Lehmann et al.(1942),Sann,Beyer(Lehmann et al.,1942), etc.,and

(2)Theories assuming that the value of horizontal displacementu(x,y)is proportional to the slope of subsidence trough profleT(x,y)(Awierszyn,1947),e.g.Knothe’s method and Ruhrkohle method.

To sum up,both the COG theory and the hypothesis of Awierszyn(1947)indicate the proportionality between the vector of horizontal displacement and the vector of subsidence trough profle slope.

2.Examples of the Gauss distribution method used to calculate mining-induced surface deformations

Most theories used for surface deformation calculations are based on the Gauss distribution function.And from it,two methods were commonly used in Europe,China and the United States.These are:Knothe’s method(Knothe,1953,1984;Sroka et al.,2011)and Ruhrkohle method(Sroka,2010;Sroka et al.,2011).In a strictly mathematical sense,both the above-mentioned methods aresimilar.They differ,however,only in their defnitions of angles limiting the horizontal range of subsidence trough,which are defned by means of the following relation:

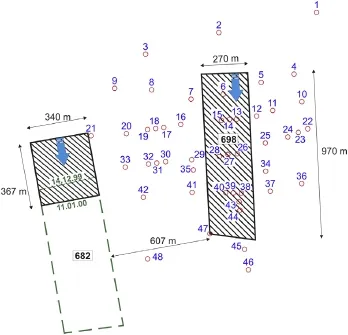
Fig.1.Situation of exploitation fronts when the deformation measurement was stopped.

whereβis the angle of main infuences’rangeaccording toKnothe’s theory,γis the limit angle of the Ruhrkohle method,andkis the coeffcient which is equal to-ln0.001.

These classic theories suggest that mining-induced surface displacement can be described by means of the function of infuences,and in the case of a three-dimensional(3D)problem, exploitation of any feld results in the subsidence of pointAon a terrain surface,which can be illustrated with the following equation:

wherew(xA,yA)is the subsidence of any pointA(mm);ais the subsidence coeffcient depending upon exploitation system,which is generally a relation of expected subsidence trough volume to a selected volume;gis the thickness of mined-out deposit(m);rK,rRare the radii of main infuences’range(m)for Knothe’s method and Ruhrkohle method,respectively;His the depth of exploitation(m); χis the parameter depending on chosen theory,χ=1 for Knothe’s method,χ=k/πfor Ruhrkohle method;dPis the surface of infnitesimally small element of mined-out deposit,and dP=dxdy;Pis the surface of mined-out space of deposit.

From the differentiation of Eq.(2),further formulae can be obtained,which may in turn help to determine the values of such surface deformation indices as:slope of subsidence trough profle at any point(Tx,Ty)(Eq.(4))or curvature of subsidence trough profle(Kxx,Kyy,Kxy)(Eq.(5)).Also horizontal displacement(ux,uy) (Eq.(6))and horizontal deformation(εx,εy)(Eq.(7)and(8)-maximum and minimum horizontal deformations)can be determined if a proper coeffcient is assumed.

Fig.2.Survey measurements contour lines along with measurements points of:(a)horizontal displacement inxdirection(mm),(b)horizontal displacement inydirection(mm).

Fig.3.Surface subsidence measurements contour line(mm)along with measurement points.

whereBis the displacement coeffcient(or horizontal deformation coeffcient).This coeffcient is then used to calculate horizontal movements and strains,assuming proportions between the slope of subsidence trough profle and horizontal movements.The hitherto determined empirical values of coeffcientB,for varied measurement bases and varied mining or geological conditions,can be defned in the following ranges(Tajduˊs,2013,2014):

(1)For coal mines:from 0.15rto 0.7r,

(2)For sulfur mines:from 0.15rto 0.26r,

(3)For copper mines:from 0.23rto 0.77r.

It also should be noted that some measurements suggest that the coeffcientBis not constant,but depends upon the position of the measurement point in the formed subsidence trough(Tajduˊs, 2013,2014).The presented range of the coeffcientBvaries widely due to the fact that disturbance depends upon the following factors:number and thickness of mined-out seams,dimensions of mined-out felds in each seam,methods of void liquidation,mining rate,geological and hydro-geological structure of overburden, tectonics,strength and strain parameters of strata.

Below,the author presents the analysis of horizontal movements for a single advancing longwall panel excavation taking into consideration the COG andTtouproportion theories.

3.Horizontal displacement analysis for the sample mine of Prosper Haniel

Analysis of horizontal displacements of the terrain surface was carried out for the sample area of the BW Prosper Haniel coal mine where the single longwall panel was excavated(DMT,2001).

In 1999,the coal mine started exploitation of the wall No.698 in the seam O/N at an average depth of 960 m.Thewidth of mined-out wall was 270 m,its panel runwas 970 m,whereas its height ranged from 3.6 m to 4.3 m.Excavation of the longwall was initiated on 10 May 1999 and terminated on 23 November 1999.After the completion of mining in the longwall No.698,nevertheless still during the measurements of subsidence and horizontal movement of measurement points,the exploitation of the longwall No.682 with the thickness of 1.6 m commenced in the seam P1 at the depthH=920 m.The situation is presented in Fig.1.

On the surface,above the Prosper Haniel coal mine,a measurement network system consisting of dispersed geodesic points was set up.Measurements were takenwith the use of GPS,which is characterized by the accuracy of below 5 mm(Sroka,2000).The frst measurement was carried out on 1 April 1999 for the points numbered from 1 to 48.The distribution of measurement points is presented in Fig.1.

Fig.4.3D analyzed mining situation along with the position of surface measurement points(at the level of+60 m).

The results of geodesic measurements taken in the period between the date of exploitation commencement of the wall No.698 and the date of 11 January 2000 indicate that the maximum subsidence measured in the central part of the trough reached thesteadystate.Only in the areaof exploitation end of thewall No.698, the points indicated their transient state.In addition,it should be noted that the layer of hard sandstone,with the thickness of approximately 90 m,occurring above the seam O/N,as well as the small dimensions of the excavated longwall No.698,caused the occurrence of partial subsidence trough on the surface.The trough was characterized by values of deformation indices lower by 50%in comparison to the values obtained during the prognosis carried out for that exploitation(Stocks and Sroka,2000).

Figs.2 and 3 present the fnal values of deformation indices obtained from geodesic measurements.For survey measurements contour lines,matching was achieved according to the Kriging method,which attributes particular weighing,called Kriging coeffcients(weighing),to the samples inside the estimation feld (sample search area)in order to minimize the mean square prediction error(Kriging variance).The author used the linear variogram with no nugget effect.

Fig.5.A spatial representation of the courses of all vector directions.

3.1.Analysis of displacement vectors-searching COG inside the strata

In the frst analysis of displacement vectors of measurement points,the author tried to fnd the area where the direction of the vectors of displacements met.To fulfll this task,the analysis of measurement points situated in the vicinity of longwall No.698 was used for a further study.Position changes of measurement points were analyzed and“virtual vectors”symbolizing the displacement of initial points(presented in Fig.4)towards the center of rock mass were marked on the basis of GPS satellite data (spatial coordinates(x,y,z)of each point).

The author made the analysis for(mining and measurements) situations where only part of longwall panel was excavated(Fig.4). Such selected situations allow for the analysis of vector displacements of surface points with only a small disturbance from created goaf(in Fig.4,the part of excavated deposit was marked with a white feld with the dimensions of 294 m×270 m).Data from a total of 48 points were available;however,the analysis did not take the points numbered as 1,7,21,47 and 48 into consideration,since the results obtained in those points could not be treated as reliable due to the occurrence of some anomalies in the values of displacement.It had been assumed that the points,whose values of measured subsidence were lower than twice the measuring error (＜5 mm),would be neglected in the study.Therefore,a total of 43 points were actually subject to analysis.A sample study of displacement direction of each measurement point was carried out on the basis of the analysis of the results of initial measurement and the measurement after 50 days from the commencement of exploitation(i.e.the ffth measurement taken on 29 June 1999).It corresponded to the mining situation with the wall advance of 294 m and with the exploitation panel opening approximate to a square(Fig.4).Fig.5 illustrates the course of all directions of displacement vectors,which appeared after matching the spatial coordinates(x,y,z)for the ffth measurement.Since the lines overlapped,which failed to produce a clear picture,it was decided that the same data should be presented by means of projecting the vectors into theyzplane,which is illustrated in Fig.6.For the sakeof better clarity and accuracy of the illustrations,the vectors of horizontal displacements were crossed with thexyplanes at the depths of 100 m,150 m,200 m,250 m,300 m,350m,400 m,500 m, 600 m,700 m,800 m and 900 m,respectively,thus creating regular sections between the planes.

Fig.6.Graphic representation of the course of all vector directions in theyzplane.

The character of the course of the majority of vectors seems to clearly indicate that the measurement points on the surface tend to displace towards the exploitation void,which appeared as a result of the excavation of the feld marked with a white rectangle.Such a situation is even more evident in the horizontalxycross-sections made at various depths(Fig.7).For example,if we study Fig.7b more carefully,presenting the displacement vectors from the initial position of measurement points to their position for the ffth measurement and the direction of those vectors to the point they cut through the horizontal plane at the depth of 250 m,it can be clearly seen that,for the considerable number of measurement points,their displacement vectors run within the feld positioned above the exploitation void.

Generally,the observations and analyses indicated that the vectors of displacements marked for the measurement points,as well as their directions,approach a particular zone with a shape of ellipsoid,which is positioned above the exploitation void.The zone can be referred to as“the COG zone”.Fig.8 presents three ellipsoids simulating the COG zone with the areas of 7667 m2for ellipse P1, 28,203 m2for ellipse P2,and 70,418 m2for ellipse P3.These ellipses were drawn for three different cross-sections at the depths of 200 m,250 m and 300 m,respectively.It was observed that at the depth of 250 m,the ellipse P1embraces 13 points crossing betweenthe section and the directions of measured vectors of displacements;ellipse P2embraces 7 such points,whereas ellipse P3embraces 11 points.

Fig.7.Displacement vectors of measurement points for characteristic cross-sections at the depths of:(a)200 m,(b)250 m,(c)300 m,and(d)350 m,respectively.

For the 40 analyzed measurement points and the sample exploitation panel of 270 m×294 m,such a zone occurs at the depth of approximately 250 m.In its vicinity,there appears to be a large concentration of vector directions marked on the basis of the measurements of 3D displacements of the given points(example in Fig.9).Only the displacement vectors of several points(i.e.16,20, 32,33 and 36)and marking their directions have a dissimilar course,which may be caused by numerous geological factors or by a measurement error.

Fig.8.Ellipses of“COG zones”(P1=1,P2=2,P3=3)for various cross-sections.

3.2.Analysis of displacement coeffcient B variations

Different approaches to the analysis of horizontal surface movements are based on the assumption that the value of horizontal displacementu(x,y)is proportional to the slope of subsidence trough profleT(x,y).But to properly calculate horizontal deformations,the value of displacement coeffcientBshould be estimated.

In order to analyze the distribution of coeffcientBvalues for the exploitation area of the longwall panel No.698 of the Prosper Haniel coal mine,as many as a dozen measurement cross-sections perpendicular to the panel length were made(Fig.10).

For the above-mentioned cross-sections,a diagram presenting the values of horizontal displacement(movements)in the direction of the cross-sectionu(α)in the function of slope value in the same cross-sectionT(α)was made.Fig.11a and b show the sample diagrams of horizontal displacement in the directionu(α)in the slope functionT(α)for the cross-sections Nos.7(a)and 12(b),respectively.

Fig.9.Graphic representation of selected vectors projected on theyzplane crossing the horizontalxyplane at the depth of approximately 250 m.

For the cross-sections presented above,function correlations between horizontal displacements and slopes were determined using linear regression method(cf.Table 1).In the formulaepresented in the table,the values of horizontal displacements were given in millimeters,whereas the slope was given in mm/m,which means that the value of parameterBis expressed in meters.

On the basis of the analysis of the matching formulae for linear regression for twelve cross-sections(Table 1),it can be observed that the results for cross-section No.1 seem barely satisfactory, whereas for the remaining cross-sections it is far more accurate, especially for all the sections from No.7.Those conclusions were verifed by analyzing the summary values for the sections No.1 to No.6(Fig.12a)to the middle of panel length,as well as for the sections No.7 to No.12(Fig.12b).

Fortheabove-mentionedsummarycross-sections,the following matching was obtained:

(1)For the sections No.1 to No.6:u(α)=-264.3T+85.1,with matchingR2=0.883;

(2)For the sections No.7 to No.12:u(α)=-170.5T+10.3,with

matchingR2=0.91.

Fig.10.Measurement cross-sections perpendicular to the longwall panel No.698.

The most likely reason for such signifcant disproportions in matching the regression lines between summary matching for sections No.1 to No.6 and No.7 to No.12 is a relatively short period of measurement duration.The completion of exploitation of the longwall panel No.698 took place on 23 November 1999 and nearly two months later(i.e.11 January 2000)these measurements were completed.Such a short measurement period for the points positioned in the vicinity of the ultimate phase of exploitation meant that in those points,the fnal stationary values of deformation indices were not obtained.In German mines,it is assumed that the minimum period necessary for reaching a fnal stationary value of deformation is approximately 3-6 months(Sroka,2010),depending on rock mass quality and exploitation depth.

For all the summary cross-sections,i.e.No.1 to No.12,the following formula was obtained:u(α)=-211.3T+31.9,with matchingR2=0.806.

Subsequently,the analysis of the distribution of the coeffcientBvalues was carried out for the cross-section perpendicular to the longwall panel No.698,crossing the middle of the longwall.The following formula for linear regression was obtained:u(α)=-190.4T+40.6,with matchingR2=0.854.

The comparison of coeffcientBfor the cross-section parallel to the panel length with that for the cross-section perpendicular to the panel length indicates that the coeffcientBfor the parallel section is approximately 10%lower than that for the perpendicular section.

The above-mentioned formulae for matching the regression lines to the measurement resultsdifferfrom theassumedhypothesis of Awierszyn(1947)by the value of the intercept.In order to approximate those values for the solution presented by Awierszyn(1947),it was assumed that the linear regression lines cross exactly in the origin.The results of such a matching were presented for several sample summary cross-sections:

Table 1Matching formulae for linear regression for the cross-sections perpendicular to the longwall panel No.698.

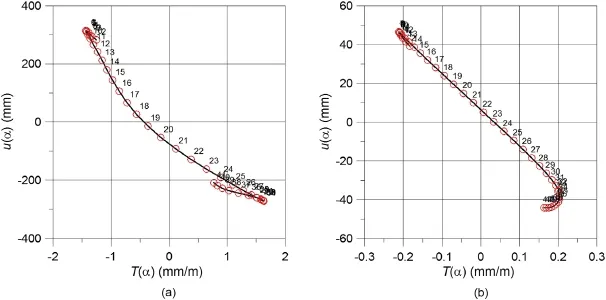
Fig.11.Horizontal displacement diagram in the cross-section directionu(α)in the slope functionT(α)for the cross-sections No.7(a)and No.12(b).

(1)For the summary cross-sections No.1 to No.6:u(α)=-237.4T, whereR2=0.755;

(2)For the summary cross-sections No.7 to No.12:u(α)=-170.8T, whereR2=0.905;

(3)For the summary cross-sections No.1 to No.12:u(α)=-205.7T, whereR2=0.779.

Fig.12.Matching formula of linear regression for the summary values of parameterBfor the cross-sections:(a)No.1 to No.6,and(b)No.7 to No.12.

For the estimated values of the horizontal deformation coeffcientB,the value of standard deviation ofS=59 mwas determined, which means that a single value of coeffcientBwas determined with the accuracy of 26%.

4.Conclusions

The prognostic values of horizontal surface displacements above a mining exploitation area still pose numerous doubts regarding their validity.Studies and observations carried out in situ seem to indicate that the following factors,inter alia,infuence the distribution of horizontal displacement:the position of a given point in relation to exploitation,rock mass properties,hydrogeological conditions,tectonics,depth of exploitation,thickness of excavated deposit,method of exploitation or speed of mining performance.

The analysis of the course of horizontal displacement vectors after excavation of wall No.698 proved logical and expected senses and directions of measured vectors.Therefore,in relation to the general character of the vector course it is justifed to assume the existing of concentration area of virtual vectors,determined on the basis of measurements of spatial displacement of points.Based on the analysis,where the strata were parted with horizontal planes (from the seam level up to the surface with interval of 50 m),it was revealed that the best agreement of the displacements vectors concentration is achieved for the depth of approximately 250 m.

Analysis of the distribution of horizontal displacement coeffcientB,carried out for the exploitation of the wall No.698 in the seam O/N of Prosper Haniel coal mine,indicated the proportionality between the horizontal displacement vector and the vector of subsidence trough slope profle.

The study also specifed that the average displacement coeffcient for cross-sections perpendicular to the advance of the mining front equalsB=205 m(B=0.21H,orB=0.47rfor tanβ=2.2).It should be noted that,according to numerous studies on the infuence of time on the distribution of measured deformations hitherto carried out in German mines,a minimum period necessary for achieving a stabilized(stationary)subsidence trough ranges between 3 and 6 months.This means that analyses for the initial cross-sections numbered as 1 and 2 were actually carried out for non-stationary deformations.The determined value of coeffcientBfor the sections numbered from 3 to 12 wasB=204 m(B=0.21H, orB=0.47rfor tanβ=2.2).

In summary,optimal matching was obtained for the sections crossing the middle of exploitation feld(No.7),as well as for sections outside the contour of the wall(Nos.11 and 12).

Confict of interest

The author wishes to confrm that there are no known conficts of interest associated with this publication and there has been no signifcant fnancial support for this work that could have infuenced its outcome.

Acknowledgments

The project was fnanced by the National Science Center of Poland granted on the grounds of decision No.DEC-2011/01/D/ ST8/07280.

Awierszyn SG.Mining-induced rock mass subsidence.Moscow,Russia:Ugletiechizdat;1947(in Russian).

Bals R.Problem of mining subsidence prediction.Stuttgart,Germany:Deutscher Markscheider-Verein e.V,Mitteilungen aus dem Markscheidewesen;1931/ 1932.s.42/43:98-111(in German).

Deutsche Montan Technologie GmbH(DMT).BW Prosper Haniel measurements point-“Schwarze Heide”.2001(not published)(in German).

Keinhorst H.Calculations of surface subsidence in Emscher.In:25 Jahre der Emschergenossenschaft 1900-1925;1925.p.53-64(in German).

Knothe S.Time infuence on shaping of subsidence trough.Archive of Mining Science 1953;1:21-31.

Knothe S.Prediction of mining infuence.Katowice,Poland:ˊSla˛sk;1984(in Polish). Lehmann K,Neubert K,Schafstein K.Calculation and presentation of ground movements above underground mining exploitation.Stuttgart,Germany:Deutscher Markscheider-Verein e.V,Mitteilungen aus dem Markscheidewesen; 1942(in German).

National Coal Board(NCB).Subsidence engineers’handbook.London,UK:Mining Department,National Coal Board;1975.

Sroka A.Surface movement measurements using GPS above turning longwall panel. In:IGSMiE PAN,Kraków,vol.1.Kraków,Poland:Kraków Publishing House; 2000.p.361-70(in Polish).

Sroka A.Infuence of exploitation velocity on surface deformation.In:IGSMiE PAN, Krakówvol.1.Kraków,Poland:Kraków Publishing House;2010.p.523-48(in Polish).

Sroka A,Tajduˊs K,Preusse A.Calculation of subsidence for room and pillar and longwall panels.In:Proceedings of the 11th Underground Coal Operations’Conference,University of Wollongong&the Australasian Institute of Mining and Metallurgy;2011.p.83-90.

Stocks S,Sroka A.Design of longwall panels for mining damage reduction.In: Proceedings of the 11th International Congress of the ISM,Kraków;2000. p.183-90(in German).

Tajduˊs K.Mining-induced surface horizontal displacement:the case of BW Prosper Haniel mine.Archive of Mining Science 2013;58(4):1037-55.

Tajduˊs K.The nature of mining-induced horizontal displacement of surface on the example of several coal mines.Archive of Mining Science 2014;59(4):971-86.

Krzysztof Tajduˊsgraduated as a Mining Engineer(2003) from AGH University of Science and Technology in Krakow (AGH-UST),Poland.He got MSc Engineer in Geomechanics. After graduation he started working for Strata Mechanics Research Institute of the Polish Academy of Sciences(2003 up today).In 2008 he defended a double Ph.D.degree:one in the feld of mining and geological engineering at AGHUST in Krakow,Poland,the other in the feld of soil mechanics at TU Bergakademie Freiberg,Germany.In 2009 he has become the youngest member of the Polish Committee on the State Mining Authority for the state of water and rock roof collapse hazard in Salt Mine“Wieliczka”S.A. Since 2010 he has been a full member of the Polish Commission of the State Mining Authority for the Surface Protection.In 2011-2014 he was working at the AGH-UST,Faculty of Drilling,Oil and Gas and from 2014 he is a guest professor at Binh Duong University,Vietnam.He has working in more than 60 projects in whole Europe related to mining-induced rock mass deformation and mining damages,rock mass stabilization,rockburst,tunneling,hydraulic fracturing,CBM.He is currently the member of ISRM and the Section of Rock Mechanics and Underground Building,Committee of Mining,Polish Academy of Sciences.

*Tel.:+48 126376200(55).

E-mail address:tajdus@img-pan.krakow.pl.

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755©2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2015.03.012