物理吸附储氢的最佳条件分析

陈宏善，刘　鑫

(甘肃省原子分子物理与功能材料重点实验室，西北师范大学物理与电子工程学院，甘肃兰州　730070)

物理吸附储氢的最佳条件分析

陈宏善，刘鑫

(甘肃省原子分子物理与功能材料重点实验室，西北师范大学物理与电子工程学院，甘肃兰州730070)

摘要：基于Langmuir吸附模型分析了物理吸附储氢的最佳条件，讨论了压强、温度及吸附热对储存量的影响．由于平衡常数随温度和吸附热按指数规律变化，存储量对温度和吸附热的依赖十分敏感．在300 K时，压强从50~100 bar降到1.5 bar的最大存储/释放量对应的吸附热约为-33.5 kJ·mol-1．

关键词：储氢；物理吸附；Langmuir模型；最优条件

世界经济的发展对能源的需求不断增长，而化石燃料的储量迅速枯竭，能源的供需矛盾是当今世界最尖锐的矛盾之一，化石燃料燃烧产生的温室气体排放及其他污染问题也使人类生存环境严重恶化，发展储量丰富、安全、清洁的新型能源是人类社会面临的最大技术挑战之一．氢的储量丰富，其热值是汽油的三倍，燃烧过程无污染，是一种潜在的理想能源，但氢能的利用需要解决一系列关键技术问题[1,2]．氢是地球上储量最丰富的元素之一，但主要以化合物形式存在，氢的规模生产技术近年来已有突破性进展[3-6]．氢的安全储运是氢能利用特别是作为车载燃料需要解决的另一关键技术．氢分子是最小的分子，分子间相互作用很弱且易泄露，传统的高压气态储存(30~70 MPa)或低温液态储存(21 K)无论从安全性或经济性考虑都是不可取的．固体材料储氢从储存密度(质量密度或体积密度)、安全性和经济性考虑都具有明显的优势[7-12]， 特别是纳米材料不仅能提供大的比表面积，还有望提供合适的吸附强度，是近年来氢能利用研究的热点之一．固体储氢可粗略分为物理吸附和化学吸附．物理吸附是氢分子吸附在比表面积很大的多孔材料的表面或孔内．由于氢分子通过弱的范德华力与主体材料发生作用，吸附较弱，储存仍需要较低的温度[7-11]． 化学吸附是氢分子首先解离后氢原子通过化学键与主体材料结合，典型的体系有Li/Na与AlH4、BH4、NH2形成的化合物[7-9,12]．由于氢的释放需要断裂强的化学键，需要较高的温度，且氢的释放一般分多步进行，虽然具有高的存储密度，但存储的氢并不能完全释放．高的存储密度和适宜的存储-释放动力学是衡量储氢材料的重要指标，美国能源部制定的储氢材料标准(2015)是储存密度为5.5wt%或每升40 g H2，储存压力为0.5~1.2 MPa，温度为-40~85 ℃．过去30年在提高氢的储存密度方面已取得了较大进展，但已有储氢材料的动力学性能离实际要求仍有很大差距．

氢的储存及释放动力学主要决定于氢与主体材料的相互作用形式及作用强度，虽然对于不同条件下吸附的热力学问题早有理论分析，但文献中给出的氢储存条件十分混乱，例如Lochan和Gordon[13]认为吸附平衡时ΔH=TΔS，由此估算 H2在-20 ℃、1~100 bar下对应的吸附热为21~32 kJ·mol-1，而50 ℃、1~100 bar的吸附热为30~42 kJ·mol-1；Yang等[14]基于范特霍夫方程分析了吸附动力学，给出的吸附热为20~50 kJ·mol-1;Bhatia和Myers[15]利用Langmuir吸附模型分析了存储条件并假定吸附的熵变为8R，给出室温下的理想吸附热为15.1 kJ·mol-1；Li等[16]根据298 K标准大气压下H2的熵为15.6R，认为理想的吸附焓变应为10~15RT， 即25~37 kJ·mol-1；Garberoglio等[17]则给出298 K、100 bar下H2的平动熵为79 J·mol-1·K-1，而吸附后H2的平动熵只是部分损失，由此得到吸附热为10~20 kJ·mol-1；Zhao等[18]给出的理想吸附热则为0.3~0.4 eV(30~40 kJ·mol-1)．常温下氢气可被视为理想气体，实验及理论分析均认为氢气的物理吸附很好的符合Langmuir吸附模型，本文给出了该模型的吸附平衡常数，分析了压强、温度及吸附热对物理吸附的影响，讨论了物理吸附储氢的最佳条件．

1Langmuir等温吸附及平衡常数

Langmuir吸附是最基本的吸附模型[19]，他假设：1)吸附质分子吸附前和吸附后分子之间无相互作用；2)吸附剂表面是均匀的，即所有吸附位是等价的且不随覆盖率变化；3)每个吸附位只能吸附一个分子，即是单层吸附．由于氢分子间的相互作用很弱，它在均匀表面的吸附能很好地满足Langmuir吸附的条件． Dinca和Long[20]测量了77 K时H2,O2,N2和CO在Mg3(O2C—C10H6—CO2)3上的吸附特性，结果表明H2与O2的吸附符合Langmuir等温线；Panella等[21]测量了77 K时H2在活性炭和单壁碳纳米管上的吸附曲线，结果也与Langmuir等温线完全一致；Sillar等[22]则基于Langmuir模型计算了温度在55~87 K之间H2在MOF-5上的吸附特性，计算的吸附等温线与相应的实验结果完全符合．

Langmuir公式最初是根据动力学分析建立的[19]． 在给定温度下吸附速率正比于气体压强及空吸附位密度[S]，而脱附速率正比于被占据的吸附位密度[A]

(1)

(2)

由此得出平衡时吸附位覆盖率θ=[A]/([A]+[S])，与压强的关系为

(3)

其中K=ka/kd是吸附平衡常数，它由温度及吸附位的性质决定．

如果假定在初始压强P1时吸附已达到平衡，则在等温条件下当压强增大到P时增加的吸附量(表面覆盖率的增量)为

(4)

对于储氢，此即为压强从P降到P1时释放的氢气量．由于在等温条件下K为常数，要得到最大的存储/释放量，则要选择合适的储存材料以提供合适的平衡常数

(5)

Langmuir模型建立后，Everett[23]、Sparnaay[24]、Honig[25]、Chakraborty[26]等对不同条件下的吸附进行了热力学分析，但早期的文献在概念上、特别是对熵的处理比较混乱，这里利用热力学与统计物理给出的基本结论讨论Langmuir吸附的平衡常数K并明确相关量的意义．

多元复相系的平衡条件为吉布斯自由能最小[27]

(6)

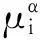
(7)

其中ΔH为吸附过程的焓变，通常称为吸附热(取正值)，表征吸附位对分子的吸附强度，ΔS为吸附过程的熵变．

把吸附前的气体当做理想气体，根据理想气体的熵(1mol)

(8)

当气体被吸附后，平动被完全限制(这既是对吸附态的定义，也是Langmuir模型的假定之一，该模型又称为Localizedmonolayermodel)，虽然转动只是被部分限制，我们稍后看到转动对熵的贡献可被忽略，而振动是被完全冻结的，因此吸附态的热力学熵近似为零．假定吸附平衡时N个分子可被吸附在M个吸附位上(覆盖率为θ=N/M)，则N个分子在M个吸附位上的分布数为

(9)

对应的构象熵为SC=klnΩ.M,N均为大数， 利用Stirling公式[28]可以得出1mol吸附态气体(N取阿伏加德罗常数)的熵为

(10)

分别将(8)和(10)式代入(7)式并取P0为标准大气压可得到

即

与Langmuir公式比较得:

(11)

由于吸附态的热力学熵为零，记ΔS0=Sg(T,P0)；而由于吸附位的性质与覆盖度θ无关，即与压强无关，同时记ΔH为ΔH0，将(11)式改写为

(11′)

(11′)式即为一些文献中给出的平衡常数．吸附平衡是能量变化与熵变竞争的结果，吸附态使体系的能量降低，而脱附变为气态使熵增加，Langmuir公式从动力学分析给出了覆盖度θ与气体压强的关系，而从热力学角度看正是考虑了气态的熵对压强的依赖关系(8)式．上面的讨论表明吸附平衡常数中的熵变是标准大气压下温度为T的气体的熵．

根据统计物理关于熵的表达式[29]

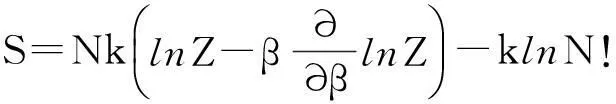
(12)

以及双原子气体的配分函数Z可以求得1molH2在1 bar和300 K时的熵， 其中平动熵为117.5 J·mol-1·K-1．根据氢分子的转动及振动光谱得到氢分子的转动特征温度θr=85.4 K和振动特征温度θv=6100 K[30]，由此得到转动的熵为13.0 J·mol-1·K-1，而常温下振动被冻结，对熵无贡献．因此在标准大气压下，1 mol H2在300K时的熵为130.7J·mol-1·K-1，这与物理化学手册给出的值一致[31]．由于氢分子的转动惯量很小,θr较高，转动对熵的贡献很小，这就是前面提到吸附后虽然转动未被完全禁止，但其熵值可忽略不计．

2压强对储氢量的影响

虽然平衡时的吸附量随平衡常数K单调增加，但要在P1与P压差之间得到最大的存储/释放量， 对应的最佳平衡常数应由(5)式决定．选取P1=1.5 bar，P分别为5，15，50，100 bar等，由(5)式确定最佳K值，图1给出了各K值对应的等温吸附线．

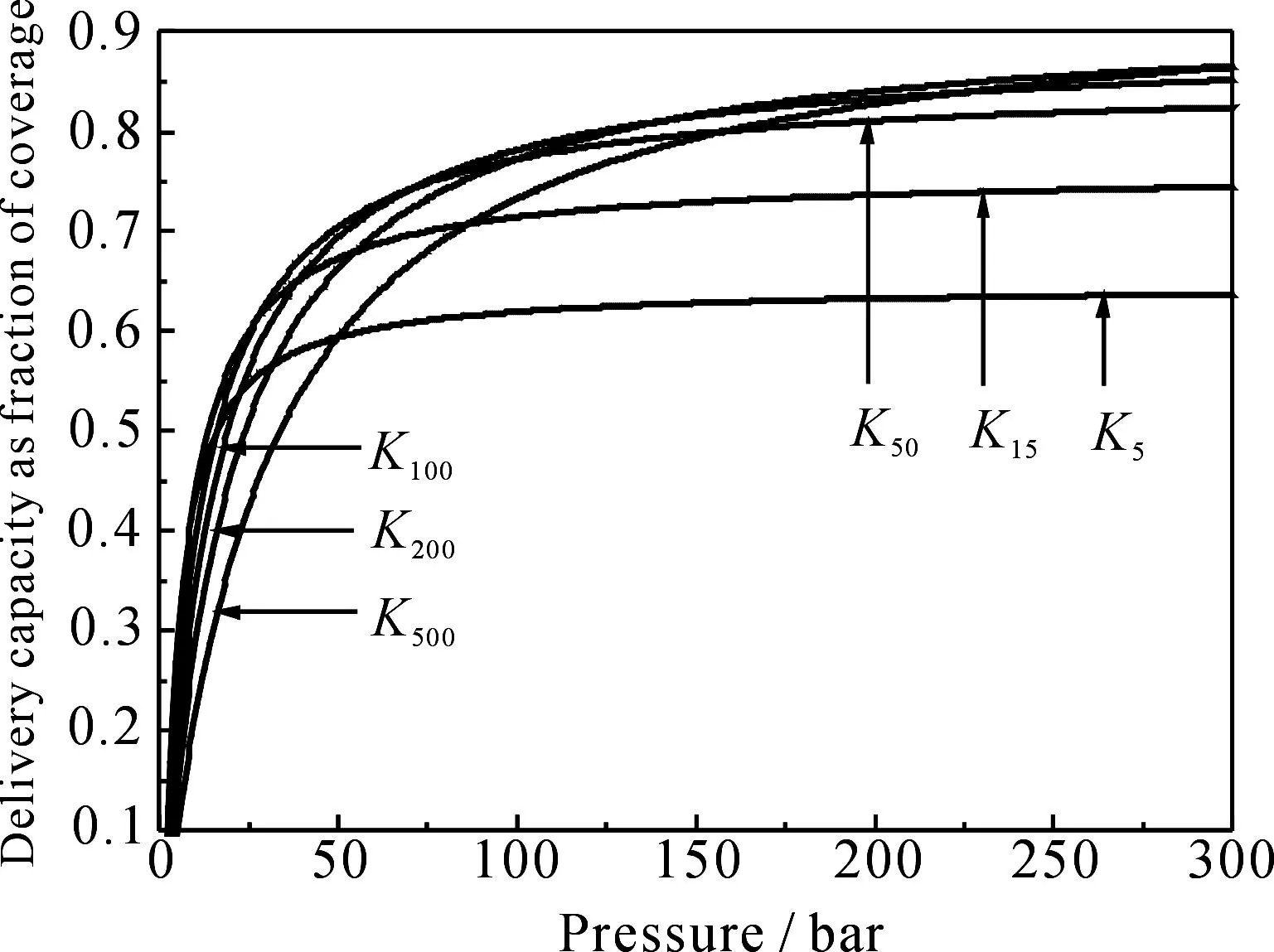
图1　　对应于压强P为5， 15， 50， 100， 200， 500 bar

图1表明如果K值较大，虽然在压强增大时吸附量迅速增大， 但在P1时吸附剂表面仍会保留大量氢分子，因此并不能得到较大的存储/释放量．如果K值太小，则吸附随压强的增加缓慢，只有在很大的压强下才能得到较大的存储/释放量．表1列出了不同压强P下各K值对应的存储/释放量Δθ．

表1　对应于各K值在P1=1.5 bar与

图1及表1数据表明，当储存压力较小时，难以得到较大的释放量;而当P很大时,增加压强,Δθ增加很小．对于一定的压强P，K值在一定范围变化时，Δθ的变化并不明显，如对于P=50 bar，K在0.058~0.211变化时，Δθ为0.66~0.70;而对于P=100 bar，K在0.058~0.115变化时，Δθ为0.77~0.78． 我们推荐的储氢压强为50~100 bar．对具有合适平衡常数的储存材料， 压强降到1.5 bar时释放的氢约为75%的表面覆盖率．对于金属有机骨架化合物(MOFs)，报导的比表面积已超过5 000 m2·g-1，如果假定吸附位的密度能达到每0.05 nm2一个，则对应75%的表面覆盖率的储氢量可达到25wt%．

3温度及吸附热对储氢量的影响

利用(4),(5)及(11′)式，很容易分析温度及吸附强度对储氢量的影响．如果在温度T及压强P~P1之间实现最大的存储/释放量Δθ，即需要(5)式要求的最佳平衡常数，则(11′)式给出吸附过程的最佳吸附焓变

(13)

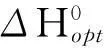
图2给出了ΔH0=-33 kJ·mol-1时不同温度下的吸附等温线．由于平衡常数随温度做指数变化，存储/释放量随温度的变化十分敏感．同样，储存材料对H2分子的吸附热对存储/释放量的影响也非常大.图2中虚线给出了ΔH0为-28和-38kJ·mol-1且T=300K时的吸附等温线．

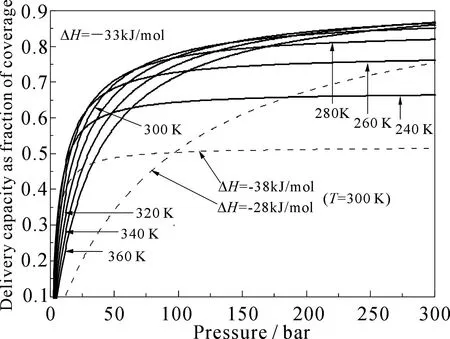
图2　　ΔH0=-33 kJ·mol-1和不同温度以及

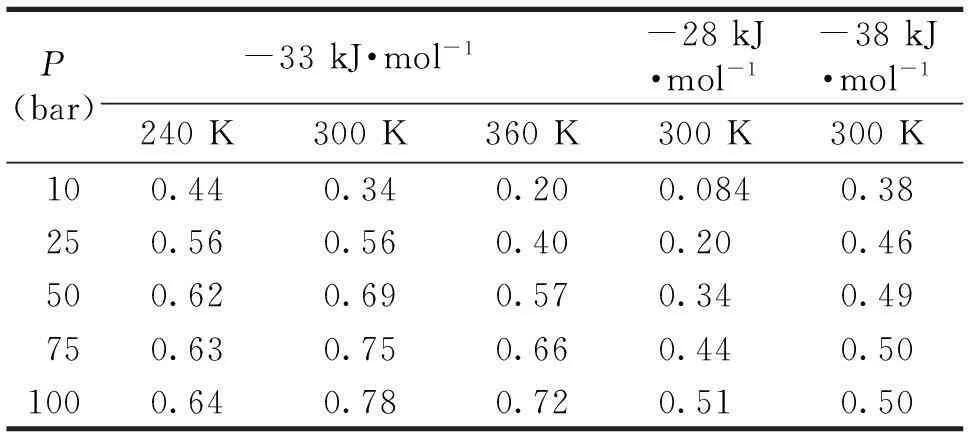
P(bar)-33kJ·mol-1-28kJ·mol-1-38kJ·mol-1240K300K360K300K300K100.440.340.200.0840.38250.560.560.400.200.46500.620.690.570.340.49750.630.750.660.440.501000.640.780.720.510.50

表2列出了不同ΔH0和不同温度条件下对应于不同压强P的存储/释放量Δθ.当ΔH0=-38 kJ·mol-1时,由于吸附太强，低压下表面保留较多的氢分子，Δθ的最大值仅为0.5；而当ΔH0=-28kJ·mol-1时,吸附量随压强增加很慢，在P=50bar时Δθ仅为0.34．我们还分析了ΔH0为-23和-43 kJ·mol-1条件下的吸附等温线， 在T=300 K和P=100 bar条件下Δθ不到0.15． 由(13)式可得到对应于T=77 K和压强P为50~100 bar的最佳焓变约为-8.6 kJ·mol-1，这对应于氢分子在大多数典型材料上的吸附热，因此现有材料只能在液氮条件下使用．

4结论

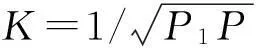
参考文献：

[1]ZÜTTELA，REMHOFA，BORGSCHULTEA，etal．Hydrogen：Thefutureenergycarrier[J].Phil Trans R SocA，2010，368：3329-3342．

[2]LUBITZ W，TUMAS B．Hydrogen：An overview[J].ChemRev，2007，107：3900-3903．

[3]DINCER I．Green methods for hydrogen production[J].IntJHydrogenEnergy，2012，37：1954-1971．

[4]MAEDA K，DOMEN K．Photocatalytic water splitting：Recent progress and future challenges[J].JPhysChemLett，2010，1：2655-2661．

[5]NAVARRO R M，PENA M A，FIERRO J L G．Hydrogen production reactions from carbon feedstocks：Fossil fuels and biomass[J].ChemRev，2007，107：3952-3991．

[6]NOCERA D G．The artificial leaf[J].AccChemRes，2012，45: 767-776．

[7]MANDAL T K，GREGORY D H．Hydrogen storage materials：Present scenarios and future directions[J].AnnuRepProgChemA，2009，105:21-54．

[8]VANDERBERG A W C，AREN C O．Materials for hydrogen storage：Current research trends and perspectives[J].ChemCommum，2008，6：668-681．

[9]EBERLE U，FELDERHOFF M，SCHÜTH F．Chemical and physical solutions for hydrogen storage[J].AngewChemIntEd，2009，48：6608-6630．

[10]SUH M P，PARK H J，PRASAD T K，et al．Hydrogen storage in metal-organic frameworks[J].ChemRev，2012，112：782-835．

[11]BARGHI S H，TSOTSIS T T，SAHIMI M．Chemisorption，physisorption and hysteresis during hydrogen storage in carbon nanotubes[J].IntJHydrogenEnergy，2014，39：1390-1397．

[12]ORIMO S，NAKAMORI Y，ELISEO J R，et al．Complex hydrides for hydrogen storage[J].ChemRev，2007，107：4111-4132．

[13]LOCHAN R C，GORDON M H．Computational studies of molecular hydrogen binding affinities： The role of dispersion force， electrostatics， and orbital interactions[J].PhysChemChemPhys，2006，8：1357-1370．

[14]YANG J，SUDIK A，WOLVERTON C，et al．High capacity hydrogen storage materials：Attributes for automotive applications and techniques for materials discovery[J].ChemSocRev，2010，39：656-675．

[15]BHATIA S K，MYERS A L．Optimum condition for adsorptive storage[J].Langmuir，2006，22(4)：1688-1700．

[16]LI J，FURUTA T，GOTO H，et al．Theoretical evaluation of hydrogen storage capacity in pure carbon nanostructures[J].JChemPhys，2003，119(4)：2376-2385．

[17]GARBEROGLIO G，SKOULIDAS A I，JOGNSON J K．Adsorption of gases in metal organic materials： comparison of simulations and experiments[J].JPhysChemB，2005，109：13094-13103．

[18]ZHAO Y F，KIM Y H，DILLON A C，et al．Hydrogen storage in novel organometallic buckyballs[J].PhysRevLet， 2005，94(15)：155504- 155508．

[19]LANGMUIR I．The adsorption of gases on plane surfaces of glass，mica and platinum[J].JAmChemSoc，1918，40(9)：1361-1403．

[20]DINCA M，LONG J R．Strong H2binding and selective gas adsorption within the microporous coordination solid Mg3(O2C—C10H6—CO2)3[J].JAmChemSoc，2005，127：9376-9377．

[21]PANELLA B，HIRSCHER M，PÜTTER H，et al．Hydrogen adsorption in metal-organic frameworks： Cu-MOFs and Zn-MOFs compared[J].AdvFunctMater，2006，16：520-524．

[22]SILLAR K，HOFMANN A，SAUER J．Ab initio study of hydrogen adsorption in MOF-5[J].JAmChemSoc，131：4143-4150．

[24]SPARNAAY M J．Physisorption on heterogeneous surfaces[J].SurfaceSci，1968，9：100-118．

[25]HONIG J M．Systematization of the thermodynamics of gas adsorption phenomena[J].JColloidInterfaceSci，1979，70：83-89．

[26]CHAKRABORTY A，SAHA B B，KOYAMA S，et al．On the thermodynamic modeling of the isosteric heat of adsorption and comparison with experiments[J].ApplPhysLett，2006，89：171901-171903．

[27]ATKINS P，DE PAULA J．Atkins’PhysicalChemistry[M].8th ed．New York： W H Freeman and Company，2006：200．

[28]ABRAMOWITZ M，STEGUN I．HandbookofMathematicalFunctions[M]. 9th ed．New York：Dover Publications，1970：257．

[29]汪志诚．热力学统计物理[M].第4版．北京：高等教育出版社，2008：213．

[30]HERZBERG G．MolecularSpectraandMolecularStructure[M].New York： Van Nostrand Reinhold Company，1950：658．

[31]LIDE D R．CRCHandbookofChemistryandPhysics[M].Boca Raton：Chemical Rubber Publishing House，1995：841．

(责任编辑孙对兄)

Optimum conditions for physisorption storage of hydrogen

CHEN Hong-shan，LIU Xin

(Key Laboratory of Atomic and Molecular Physics & Functional Materials of Gansu Province，

College of Physics and Electronic Engineering， Northwest Normal University， Lanzhou 730070，Gansu,China)

Abstract:In this paper，the optimum storage conditions are discussed based on the Langmuir isotherm model．We analyze the adsorption equilibrium constant and elucidate the quantities involved．The effect of pressure，temperature and the heat of adsorption on the uptake-release are discussed．As the equilibrium constant changes with temperature and the heat of adsorption exponentially，the uptake-release capacity depends sensitively on them．For maximum delivery pressure between 50 to 100 bar and P1=1.5 bar at ambient temperature，an adsorption enthalpy change about -33.5 kJ·mol-1is desired．

Key words:hydrogen storage；physisorption；Langmuir model；optimum conditions

中图分类号：O 642； O 647

文献标志码：A

文章编号：1001-988Ⅹ(2015)02-0032-05

作者简介：陈宏善(1963—)，男，甘肃金塔人，教授，博士,博士研究生导师.主要研究方向为原子与分子物理和材料粘弹性.E-mail:chenhs@nwnu.edu.cn

基金项目:国家自然科学基金资助项目(11164024)

收稿日期：2014-11-10;修改稿收到日期:2014-12-28