古德曼函数及其在求解非线性演化方程中的应用

石玉仁,王雪玲,王林雪,宗　谨,杨红娟

(西北师范大学物理与电子工程学院,甘肃兰州　730070)

古德曼函数及其在求解非线性演化方程中的应用

石玉仁,王雪玲,王林雪,宗谨,杨红娟

(西北师范大学物理与电子工程学院,甘肃兰州730070)

摘要：基于最小二乘法的思想基础，提出了一种用古德曼函数构造非线性演化方程孤立波解的半解析方法.以Burgers方程和KdV方程为例，发现该方法给出的孤波解与相应的精确解吻合得很好.该方法也可以推广到求解其他非线性演化方程的孤立波解.

关键词：古德曼函数;最小二乘法;孤立波解

非线性科学是目前科学研究的热点问题之一,求解非线性偏微分方程,是非线性科学的一重要组成部分,也是物理学家和数学家研究的重要课题.随着孤立子理论的发展,许多学者提出了一系列构造非线性方程精确解的方法,如反散射法,Backlund变换法,Darboux变换法,Hirota双线性法,Painleve分析法及近年发展的齐次平衡法[1-3],双曲函数法[4-6],Jacobian椭圆函数法[7,8],辅助方程法[9]等.很多方法可借助计算机代数系统如Maple,Mathematica等快速高效地完成.尽管已有很多求解非线性演化方程精确解的方法,但由于问题的复杂性,至今尚无统一的求解方法.另外绝大多数非线性方程的精确解仍无法得到;能够得到精确解的非线性方程仍是凤毛麟角.

古德曼函数是德国数学家克里斯托夫·古德曼(Christof Gudermann,1798—1852年)提出的一类特殊函数.该函数的提出已有悠久的历史,但对它进行介绍的文献比较少.本文对古德曼函数及其与三角函数、双曲函数之间的关系进行了介绍,并提出了一种用古德曼函数构造非线性演化方程孤立波解的半解析方法.文中用该方法求解了Burgers方程的扭结型孤立波解和Korteweg-de Vries(KdV)方程的钟型孤立波解,发现该方法给出的近似解与相应的精确解符合得很好.

1古德曼函数简介

古德曼函数可把三角函数与双曲函数直接联系起来而不用借助复数.它的定义如下[10]:

arcsin(tanhx)=arctan(sinhx)=

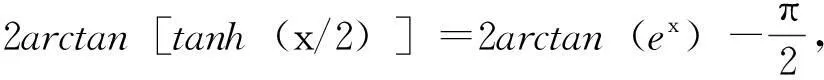
(1)

singdx=tanhx,cscgdx=cothx,

cosgdx=sechx,secgdx=coshx,

tangdx=sinhx,cotgdx=cschx,

由关系可知,凡是能用双曲函数表示的孤立波,也可用古德曼函数表示.

单摆方程

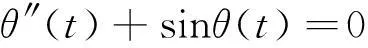
(3)

的一个精确非周期解可以用古德曼函数表示为θ(t)=2gdt,其角速度θ′(t)=2secht具有钟状孤立波结构.在使用墨卡托(Mercato)投影法的地图中,若以y表示一个地点跟赤道之间的距离,则该点的纬度φ与y的关系为φ=gdy.

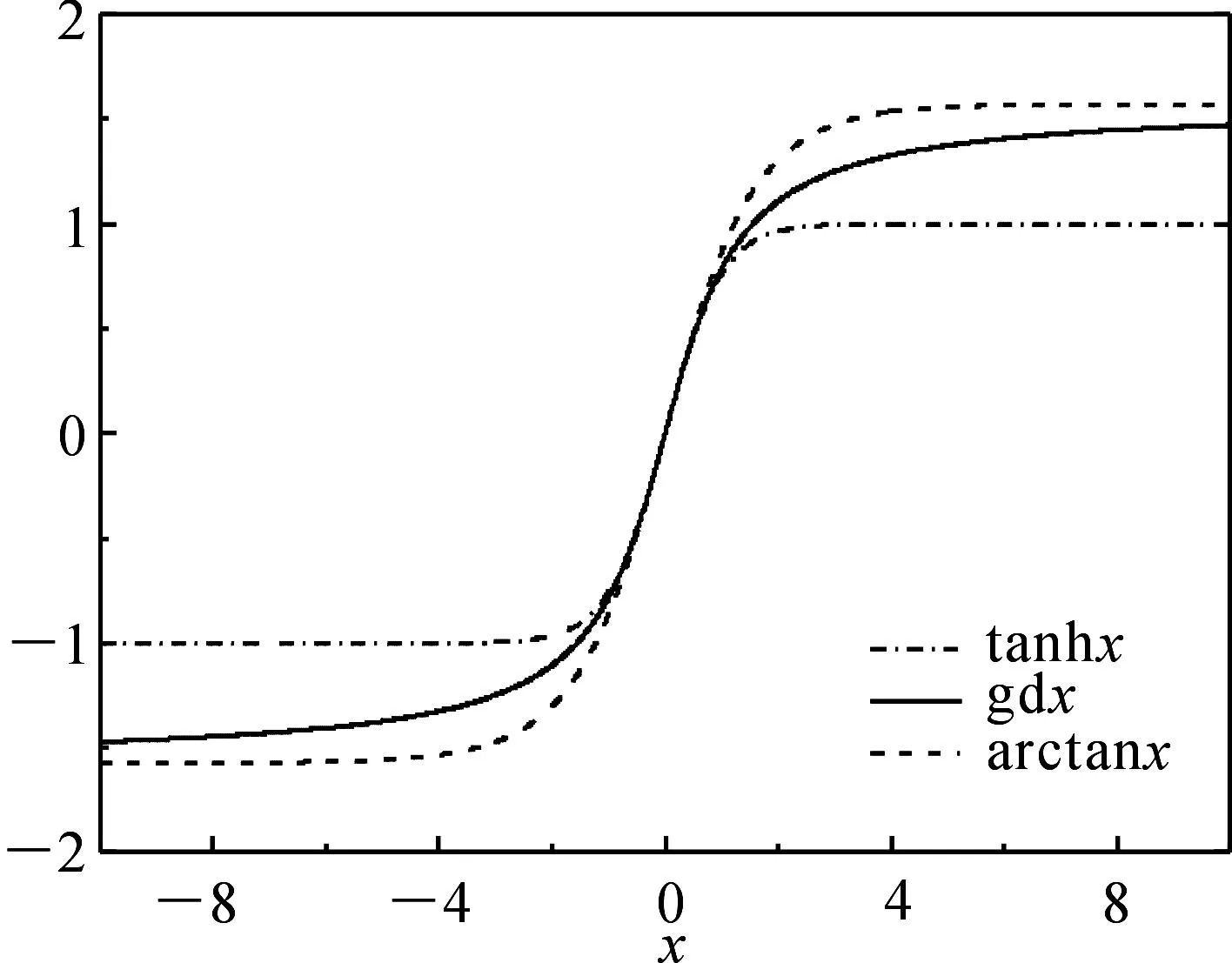
图1　古德曼函数、反正切函数与双曲正切函数的图像

2用古德曼函数求解非线性演化方程的孤立波解

2.1函数引入

为应用方便,引入下列函数

(4)

函数f(ξ,W)为奇函数，其具有扭结状或反扭结状结构，图像与反正切函数或双曲正切函数的图像类似.这一点启发我们：可以利用函数f来构造非线性演化方程的扭结状孤立波解.

我们引入下列函数

(5)

函数g(ξ,W)为偶函数，具有钟状结构，可以用来构造非线性演化方程的钟状孤立波解；其满足边界条件

(6)

2.2Burgers方程的冲击波解

Burgers方程是物理学和数学中经常出现的重要的非线性波动方程之一.如声波在具有粘滞性和热传导性的介质中传播,若不考虑介质的频散特性和弛豫过程,控制方程在一定条件下就可以归结为Burgers方程[11].下面举例说明用古德曼函数构造Burgers方程的扭结型孤立波解(近似),该法也可以推广到求解其他方程.

考虑如下形式的Burgers方程

(7)

其中,α,β为非线性项和耗散项系数，分别表征了非线性相互作用和耗散强度.引入行波变换

(8)

其中,k和ω分别为波数和圆频率，x0为任意常数.把(8)式代入方程(7),并对ξ积分一次,取积分常数为0,得到

(9)

当ξ→±∞时，φ′(ξ)→0，故有边界条件

(10)

设方程(9)有近似解

(11)

(12)

一般情况下，(11)式不是方程(9)的精确解.将其代入方程(9)后,记残差为

(13)

可采用2-范数衡量残差的大小

(14)

把(12)式代入方程(9)左边,经过简单运算,得

(15)

进一步得到

(16)

其中

(17)

(18)

代入(16)式，得残差的极小值

(19)

可以看出,残差随着ω的增加而增加，但不随波数k的改变而发生改变.后面与精确解的比较表明，尽管ω增加时(其他参数固定)该解与精确解之间的绝对误差(最大值)增加,但相对误差的增加并不明显；而且近似解与精确解仅仅在很小的区间内有相对较大差别，在大范围内，两者差别非常小.这样，得到方程(9)用古德曼函数表示的一近似解析解

(20)

(20)式表示的近似解具有较高的精度.为表明这一点,不妨与方程(9)的精确解

(21)

α=6,β=1,ω=1,x0=0

2.3KdV方程的孤立子解

考虑如下形式的KdV方程

(22)

其中,α,β为非线性项和色散项系数，分别表征非线性相互作用和色散强度.引入行波变换(8)式后，方程(22)化为关于ξ的常微分方程；该方程两边对ξ积分一次,并取积分常数为0,得

(23)

这里寻找KdV方程的钟型孤立波解，故有边界条件

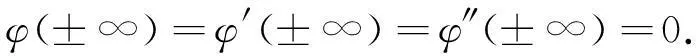
设方程(23)有近似解

(24)

其中,a0,a1和W为待定常数.不失一般性,假设W>0.此时由边界条件得a0=0，故设

(25)

(26)

与前面类似，仍采用2-范数衡量残差的大小，并使残差取极小值以确定a1与W.

把(25)式代入方程(23)左边,经过简单运算,得

(27)

进一步，得

(28)

其中,

0.7577221;

0.8856813;

(29)

图3给出了不同k时近似解与精确解的波形图.可以看出，仅在很小的空间范围内，两者有较明显差别；除此范围外，两者符合得非常好，说明前面提出的用古德曼函数构造KdV方程的孤立波解是行之有效的.

α=6,β=1,ω=4β k3,x0=0

值得说明的是，对于方程近似解的拟设，选择时有很大的自由性.通过选择合适的拟设解，可能会得到更好的结果.事实上，对于KdV方程的孤立波解，若采取下列拟设，将得到一个更好的近似解.

(30)

(31)

α=6,β=1,ω=4βk3,x0=0

3结论

本文对古德曼函数进行了介绍，并提出了一种利用古德曼函数构造非线性演化方程孤立波解的半解析方法.这种方法的理论基础是谱方法中的最小二乘法.文中以Burgers方程和KdV方程为例说明了该方法，并将该方法得到的近似解与相应的精确解进行了对照，发现该方法给出的解与精确解符合得很好.该方法可用于一大类非线性演化方程孤立波的求解，对于某些非线性问题的解决，具有积极的意义.

参考文献：

[1]WANG Ming-liang.The solitary wave solutions for variant Boussinesq equations[J].PhysLettA,1995,199:169-172.

[2]WANG Ming-liang,ZHOU Yu-bin,LI Zhi-bin.Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].PhysicsLettersA,1996,216:67-75.

[3]范恩贵,张鸿庆.非线性孤子方程的齐次平衡法[J].物理学报,1998,47(3):353-362.

[4]张桂戌,李志斌,段一士.非线性波方程的精确孤立波解[J].中国科学:A辑,2000,30(12):1103-1108.

[5]吕克璞,石玉仁,段文山,等.KdV-Burgers方程的孤波解[J].物理学报,2001,50(11):2074-2076.

[6]石玉仁,吕克璞,段文山,等.组合KdV方程的显式精确解[J].物理学报,2003,52(2):267-270.

[7]刘式适,傅遵涛,刘式达,等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报,2001,50(11):2068-2073.

[8]刘式适,傅遵涛,刘式达,等.一类非线性方程的新周期解[J].物理学报,2002,51(1):10-14.

[9]套格图桑，斯仁道尔吉.辅助方程构造(2+1)维Hybrid-Lattice系统和离散的mKdV方程的精确解[J].物理学报,2007,56(2):627-636.

[10]ZWILLINGER D,CRCStandardMathematicalTablesandFormulae[M].Boca Raton:CRC Press,2003:530-531.

[11]钱祖文.非线性声学[M].北京:科学出版社,1992:73-91.

E-mail:shiyr@nwnu.edu.cn

Gudermann function and its application for

solving nonlinear evolution equations

SHI Yu-ren,WANG Xue-ling,WANG Lin-xue,ZONG Jin,YANG Hong-juan

(College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,Gansu,China)

Abstract:Based on the thought of the least square method,a semi-analytical method,in which the Gudermann function is applied,is presented for obtaining the solitary wave solutions of a class of nonlinear evolution equations.As an example,this method is applied to find the solitary wave solutions of the Burgers equation and the KdV equation.The solitary wave solutions are agreement well with the exact ones.The method presented in this paper can also be generalized to find the solitary wave solutions of a class of nonlinear evolution equations.

Key words:Gudermann function;the least square method;solitary wave solution

中图分类号：O 411.1

文献标志码：A

文章编号：1001-988Ⅹ(2015)02-0037-05

作者简介：石玉仁(1975—)，男，甘肃金昌人，教授，博士.主要研究方向为非线性物理.

基金项目:国家自然科学基金资助项目(11047010)

收稿日期：2014-09-20;修改稿收到日期:2014-11-25