一种改进的基于RSSI最小二乘法和拟牛顿法的WSN节点定位算法

王坚+程星晶+刘继乾+文永江

摘要：针对受周围环境影响的无线传感器网络定位精度等因素引起的测量误差问题，提出一种改进的基于RSSI最小二乘法和拟牛顿法的定位算法。本文首先利用最小二乘法预估未知节点的初步位置，再将节点位置作为拟牛顿算法的初始值进行迭代计算，得到更为精确的节点位置。仿真结果证明，该算法能有效地抑制测距传播误差，提高传感节点的定位精度。

关键词：无线传感器网络；节点定位算法；最小二乘法；拟牛顿法

中图分类号：TN929 文献标识码：A 文章编号：1009-3044（2016）27-0222-04

Abstract： In order to reduce the measurement error by the surrounding environment influence when the signal is transmitting to improve the positioning accuracy， this paper proposes a kind of the localization algorithm that is the least squares method combined with the quasi Newton method. First， using the least square method to estimates the unknown node， and get the initial position of the unknown node， then putting the node position as a quasi Newton algorithm of the initial value to iterative calculation， getting more exact node location. Simulation outcomes display that the algorithm can impactfully decrease the influence of the error in propagation process and improve the accuracy of the sensor node localization， and the algorithm needs no any additional hardware equipment， so it is achieved likely.

Key words： wireless sensor networks； the node localization Algorithm； the least square method； quasi Newton method

节点定位技术是无线传感器网络WSN（wireless sensor network）关键支撑技术，具有非常重要意义的研究价值。

基于距离（接收信号强度指示）的RSSI（Received Signal Strength Indicator）算法，因其勿需新增额外硬件设备、能耗低和易实现等优势成为WSN节点定位技术的研究热点[1]。

在现有研究的基础上[7] [8] [9] [10]，本文提出了一种改进的基于RSSI最小二乘法和拟牛顿法的WSN节点定位算法。首先利用最小二乘法预估未知节点的初步位置，再将节点位置作为拟牛顿算法的初始值进行迭代计算，得到更为精确的节点位置。仿真结果证明，该算法能有效地抑制测距传播误差，提高了传感节点的定位精度。

1 最小二乘法和拟牛顿法

1.1 无线电传播路径损耗模型

RSSI定位算法定位精度受无线电传播路径损耗的影响很大。综合考虑到实际应用环境中多径、绕射、障碍物等因素影响[2]，对数-常态分布模型[4]将更加趋近实际无线环境，通过信号强度的路径损耗，可以计算出节点到所收到信标节点的预估位置。

可求解出，因存在测距误差，值尽可能使误差模型达到最小值，最后利用最小均方预估可得未知节点坐标为。

1.3 拟牛顿法

拟牛顿法[3]主要有DFP和BFGS两种形式，其原理是通过引入牛顿条件在试探点附近的二次逼近从而确定线搜索方向。本改进算法选用BFGS算法。

2 一种改进的基于RSSI最小二乘法和拟牛顿法的WSN节点定位算法

2.1 算法流程

Step 1 布置锚节点。先把n个锚节点分别布置到指定的位置，锚节点的坐标为，标志位为“1”。

Step 2 建立和更新邻居表。当未知节点加入到无线传感器网络中，未知节点使用接收到的锚节点和未知节点的信号强度，建立自己的邻居表，邻居表中存储着一跳范围内的所有节点的RSSI、距离（利用信号传播损耗公式进行换算得出）和一跳范围内的锚节点的坐标信息，并把自己的标志位，标志为“0”。

Step 3 利用最小二乘法计算未知节点的位置。当未知节点收到3个或者3个以上的锚节点信号强度时，对锚节点的RSSI从强到弱进行排序，筛查出超过阈值信号强度的锚节点，运用最小二乘法计算未知节点位置。

Step 4 更新未知节点的标志位。把能够利用最小二乘法成功定位的未知节点的标志位更新为“2”。

Step 5 选取BFGS的初始数据。把经过最小二乘法计算出来的坐标信息作为BFGS的初始值，和初始矩阵，给定允许误差；

Step 6 核对是否满足终止准则条件。计算，如果，迭代终止，则是问题的近似最优解；否则转Step 3。

Step 7 构造初始方向。取，且令。

Step 8 进行一维搜索。求出和，使得

Step 9 核对是否满足终止准则条件。计算，若，迭代终止，则是问题的近似最优解；否则转Step 6。

Step 10 检查迭代次数。若，令，转Step 3；否则转Step 7。

Step 11构造初始方向。用公式

计算出，取，令，返回Step 4。

其中：

Step 12 更新能未知节点的信息。把经过BFGS进行计算过的坐标信息作为最终计算结果，并把消息以广播的方式告诉周围的节点。

Step 13 特殊情况处理情况。当未知节点收到三个或者三个以上的锚节点在同一直线上时，如图1所示，黄色圆为锚节点，浅蓝色为未知节点的真实坐标。在这种情况下，未知节点通过最小二乘法是无法计算出未知节点的具体位置时。本文中提出中的最小二乘法和结合法可以大大的改进此特殊情况。

2. 2目标函数

假设在一个边长为的正方形区域，共有个传感器节点，其中有个未知节点，编号是，个锚节点，编号是。个节点的坐标向量为，其中。，表示未知节点的估计位置与邻居锚节点之间的距离；是未知节点与邻居锚节点之间的测量距离，如果信号传播的时候没有损耗，则应该等于。综合考虑到实际应用环境中多径、绕射、障碍物等因素影响，无线电传播路径损耗与理论值存在差异，所以我们对进行定义：，是未知节点收到的任意两锚节点间的信号强度，为信号损耗系数。更好的反映未知节点周围的环境情况。

3 实验仿真与结果分析

利用Matlab，对本文提出的改进算法与最小二乘法在二维空间内无线网络节点定位的三方面性能（定位精度、测距误差对定位精度的影响和节点通信半径对定位精度的影响）进行仿真比较。

设定为成功定位的未知节点的最终计算结果，为成功定位的未知节点的真实位置。

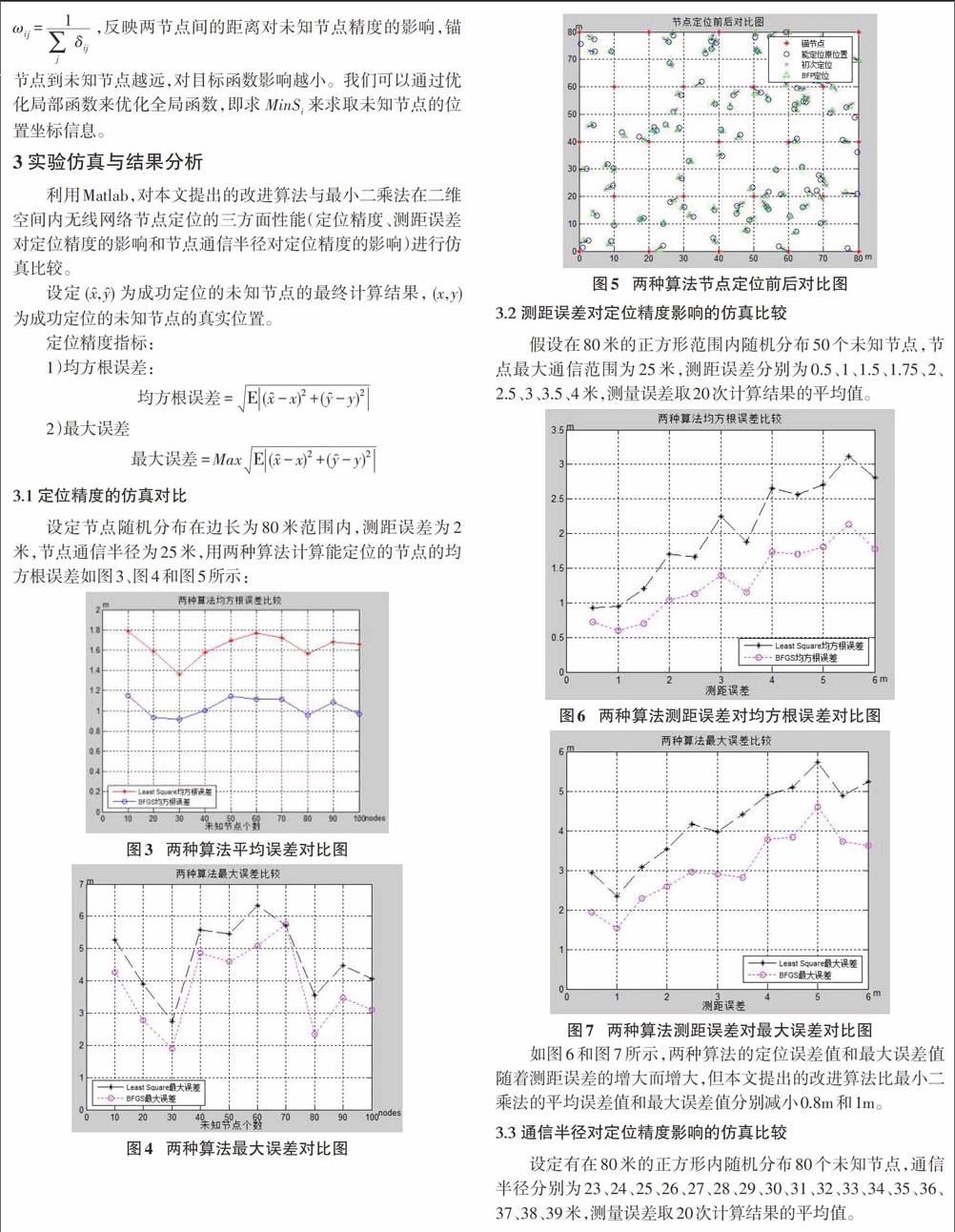
3.1 定位精度的仿真对比

设定节点随机分布在边长为80米范围内，测距误差为2米，节点通信半径为25米，用两种算法计算能定位的节点的均方根误差如图3、图4和图5所示：

3.2 测距误差对定位精度影响的仿真比较

假设在80米的正方形范围内随机分布50个未知节点，节点最大通信范围为25米，测距误差分别为0.5、1、1.5、1.75、2、2.5、3、3.5、4米，测量误差取20次计算结果的平均值。

如图6和图7所示，两种算法的定位误差值和最大误差值随着测距误差的增大而增大，但本文提出的改进算法比最小二乘法的平均误差值和最大误差值分别减小0.8m和1m。

3.3 通信半径对定位精度影响的仿真比较

设定有在80米的正方形内随机分布80个未知节点，通信半径分别为23、24、25、26、27、28、29、30、31、32、33、34、35、36、37、38、39米，测量误差取20次计算结果的平均值。

如图8所示，最小二乘法的均方根误差的平均值约为1.5米，而本文提出的改进算法均方根误差的平均值约为0.8米；如图9所示，本文提出的改进算法的最大误差比最小二乘法减少1米，定位精度提高了40%。

4 总结

本文提出了一种改进的基于RSSI最小二乘法和拟牛顿法相结合的定位算法。此改进算法首先运用最小二乘法预估未知节点的初步位置，其次运用将节点位置作为拟牛顿算法的初始值进行迭代计算，得到更为精确的节点位置。实验结果表明，本文提出的算法平均误差在1 米左右，最大误差在4米左右，更有效地抑制测距传播误差，提高传感节点的定位精度，同时该算法保留了设备简单、低能耗和易实现等优点。

参考文献：

[1] 孙利民.无线传感器网络[M].北京：清华大学出版社. 2005.5.

[2] 张宏君，毛永毅.改进的无线传感器网络节点定位算法[J].计算机应用，2012.32（8）： 2103-2105.

[3] 谢政，李建平，汤泽滢.非线性最优化[M].长沙：国防科技大学出版社.2003.9.

[4] 张洁颖，孙懋珩，王侠.基于RSSI和LQI的动态距离估计算法[J].电子测量技术， 2007.30（2）：142-145.

[5] Jungang Zheng， Chengdong Wu， Hao Chu， et al. Localization algorithm based on RSSI and distance geometry constrain for wireless sensor network. In 2010 International Conference on Electrical and Control Engineering.

[6] Wen-Hsing Kuo， Yun-Shen Chen， Gwei-Tai Jen， et al. An Intelligent Positioning Approach： RSSI-Based Indoor And Outdoor Localization Scheme In ZigBee Networks. Proceedings of the Ninth International Conference on Machine Learning and Cybernetics， Qingdao， 11-14 July 2010.

[7] Yuanqing Qin， Chunjie Zhou， Shuang-Hua Yang， et al. A Distributed Newton Iteration Based Localization Scheme in Underground Tunnels. UKACC International Conference on Control 2012 Cardiff， UK， 3-5 September 2012.

[8] Qingguo Zhang， Jinghua Wang， and Cong Jin. A Distributed Node Localization Algorithm for WSNs Based on the Newton Method. In Wireless Communications， Networking and Mobile Computing （WiCOM）， 2011 7th International Conference.

[9]陶为戈，朱昳华，贾子彦.基于RSSI混合滤波和最小二乘参数估计的测距算法[J].传感技术学报，2012，25（ 12） ： 1748-1753.

[10]王新芳，张冰，冯友兵.基于粒子群优化的改进加权质心定位算法[J].计算机工程，2012（1） ： 90-92.