Ni26+离子态分辨光复合过程的R矩阵理论研究

颉录有，马　驰，马　堃，董晨钟，张登红

(甘肃省原子分子物理与功能材料重点实验室，

西北师范大学物理与电子工程学院，甘肃兰州　730070)

Ni26+离子态分辨光复合过程的R矩阵理论研究

颉录有，马驰，马堃，董晨钟，张登红

(甘肃省原子分子物理与功能材料重点实验室，

西北师范大学物理与电子工程学院，甘肃兰州730070)

摘要：利用基于相对论R矩阵理论的DARC程序系统计算了Ni25+离子基态1s22s(2S1/2)和激发态1s22p(2P1/2,2P3/2)的光电离截面，并通过细致平衡原理获得了统一的光复合过程(即辐射复合和双电子复合)态分辨的截面，计算结果给出了辐射复合与双电子复合过程间的干涉效应.为了标识和分析KLL共振能区所有的共振峰，基于相对论组态相互作用理论(RCI)的FAC程序被用来计算共振峰的能量、强度及其相关的双激发态的辐射、俄歇跃迁几率以及共振宽度等.利用统一的光复合截面进一步得到了KLL双电子复合过程的伴线强度，并与孤立共振近似下FAC的计算结果以及以前的理论和实验结果进行了比较，对存在的一致性和偏差进行了分析和讨论.

关键词：光复合截面;相对论R矩阵理论;共振能量;共振强度

在高温、低密等离子体(如太阳、磁约束聚变装置等产生的等离子体等[1])中，高电荷态离子的光复合过程强烈影响着等离子体的电离平衡及辐射X光谱[2-4].高电荷态离子的光复合(PR)主要包括非共振的辐射复合(RR)过程和共振的双电子复合(DR)过程[5].辐射复合指靶离子直接俘获自由电子到其束缚态，同时放出一个光子的过程；双电子复合是一个间接过程，靶离子首先俘获自由电子，同时内部一个束缚电子被激发，形成共振双激发态，共振态不稳定将进一步通过辐射光子跃迁到低能态.RR与DR过程有着相同的初、末态，两种过程之间存在干涉[4].以往的理论研究对光复合过程的处理多采用独立过程和孤立共振近似，忽略了RR与DR过程间的干涉以及重叠态间的干涉[8].近年来，在统一的理论框架下处理DR和RR过程的理论，如投影算符近似[6]、密耦合近似下的扭曲波理论[4,7]以及R-矩阵理论[8-11]等已被建立，其显著的特点是DR与RR之间的干涉和重叠态间的干涉能够被予以很好地考虑，利用这些理论人们已开展了一系列研究，并取得了很好的结果[12-18].实验方面，随着重离子储存环、电子束离子阱(EBIT)等实验装置及相关测量技术的不断提高，人们已开展了许多高电荷态离子，如U90+,Hg75+…78+和Bi79+光复合过程的研究[19-21]，并观测到了显著的DR与RR间的干涉[19-22].

类He离子是高温天体、实验室等离子体中重要的电荷态离子，其光复合过程产生的X射线谱，特别是DR过程的双电子伴线对等离子体中电子温度及非麦克斯韦的电子分布十分敏感，是等离子体诊断的重要工具[1-3]；同时，由于类He离子简单的结构，常被人们选作细致揭示相对论效应、电子关联效应及其检验理论和实验的重要体系[23].

Ni是天体中重要的高丰度元素，本文将重点以类He的Ni26+离子为例，利用基于全相对论R-矩阵理论的计算程序DARC(the Dirac Atomic R-matrix Codes)[24]并结合基于相对论组态相互作用的FAC(the Flexible Atomic Code )程序[25]开展其光复合过程的研究.相对论R-矩阵理论由于其系统考虑了相对论效应，并能给出精细的共振结构，目前已被广泛用于高电荷态离子光电离、电子碰撞激发等过程的研究中[26]，但对于光复合过程，由于计算的复杂性，相关的研究工作十分匮乏.本文一个重要目的即为检验该理论在处理高电荷态离子光复合过程中的有效性和精确性.

1理论方法

1.1光复合截面

在KLL共振能区，即靶离子俘获自由电子到L壳层，同时激发其K壳层束缚电子到L壳层的能量区间，Ni26+离子态分辨的光复合过程可以表示如下

(1)

其中,(a),(b)和(c)表示可能的双电子复合过程的通道及其形成的中间双激发态;(d)和(e)表示辐射复合(或双电子复合)过程的末态.

在全相对论R-矩阵理论中，具有N电子的靶离子与自由电子复合形成(N+1)电子体系的Dirac-Coulomb 哈密顿量可以表示为[6]

(2)

其中，第一项描述了单电子的动能和势能；第二项表示电子-电子间的库伦相互作用;i和j分别表示第i和j个电子;Z为核电荷数;α和β为狄拉克矩阵.

在密耦合近似下，(N+1)电子体系的波函数可以表示为[6]

(3)

根据细致平衡原理，在电偶极近似下，处于初态精细能级j的靶离子俘获自由电子形成(N+1)电子体系的光复合末态i的PR截面可以表示为[27]

(4)

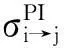
(5)

其中，gi为光电离初态的统计权重;c为光速;ω为光子能量;Mi→j为光电离矩阵元

(6)

其中，Ψi和Ψj分别为光电离初、末态的波函数;D为电偶极辐射场算符.

目前研究中，为了获得高精度的光电离截面，基于相对论多组态Dirac-Fock(MCDF)理论[28]的GRASP2K程序包[29]被用来计算Ni26+离子的靶态波函数，计算中包括了1snl(n=1~5,l=0,1,…,n-1)共15个组态，49个精细能级.不同角动量的连续电子的波函数由30个基函数线性组合而成.为保证能够分辨所有精细的共振峰，在光电离截面的计算中，选取了10-3Ry的光电子能量步长.表1给出了目前利用相对论R矩阵和MCDF理论并考虑相同电子关联的情况下计算所得49个靶态的精细结构能级，作为比较，表中也给出了NIST数据[30].从表中可以看出，MCDF理论结果与NIST数据符合的非常好，R矩阵理论的结果与NIST数据有大约0.1%的偏差，经分析其主要来自Breit相互作用的影响，该效应在目前的R矩阵程序中没有被考虑[24].图1给出了目前计算所得Ni25+离子基态1s22s(2S1/2)和激发态1s22p(2P1/2,2P3/2)的光电离截面，从图中可以看出，目前计算在长度(L)和速度(V)两种规范下的结果符合的非常好，反应了目前计算对电子关联效应的考虑是比较完善的.

1.2光复合共振线的强度

光复合截面的共振峰包含了DR过程双电子伴线的信息，共振峰的中心位置对应共振能量.由于DR与RR间的干涉，共振峰通常呈现非对称分布，即Fano线型[31].通过对光复合截面在共振能量εs附近区域积分，可以获得DR过程双电子伴线的强度

(7)

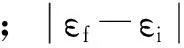
在独立过程和孤立共振近似下，DR过程的伴线强度也可以通过下式获得[32]

表1　Ni26+离子能级(eV)的比较

(8)

其中,i,d,f分别为DR过程的初态、中间双激发态和末态;σDR(ε)为双电子复合截面;Edi为共振能量;gi和gd分别为初态i和中间双激发态d的统计权重;Aa和Ar分别为Auger几率和辐射跃迁几率;求和下标i′和f′表示遍及中间态d到所有可能的Auger末态i′和辐射末态f′.对所有可能末态f对应的Sidf进行求和进一步可以获得给出初态下某一共振态的DR伴线强度.

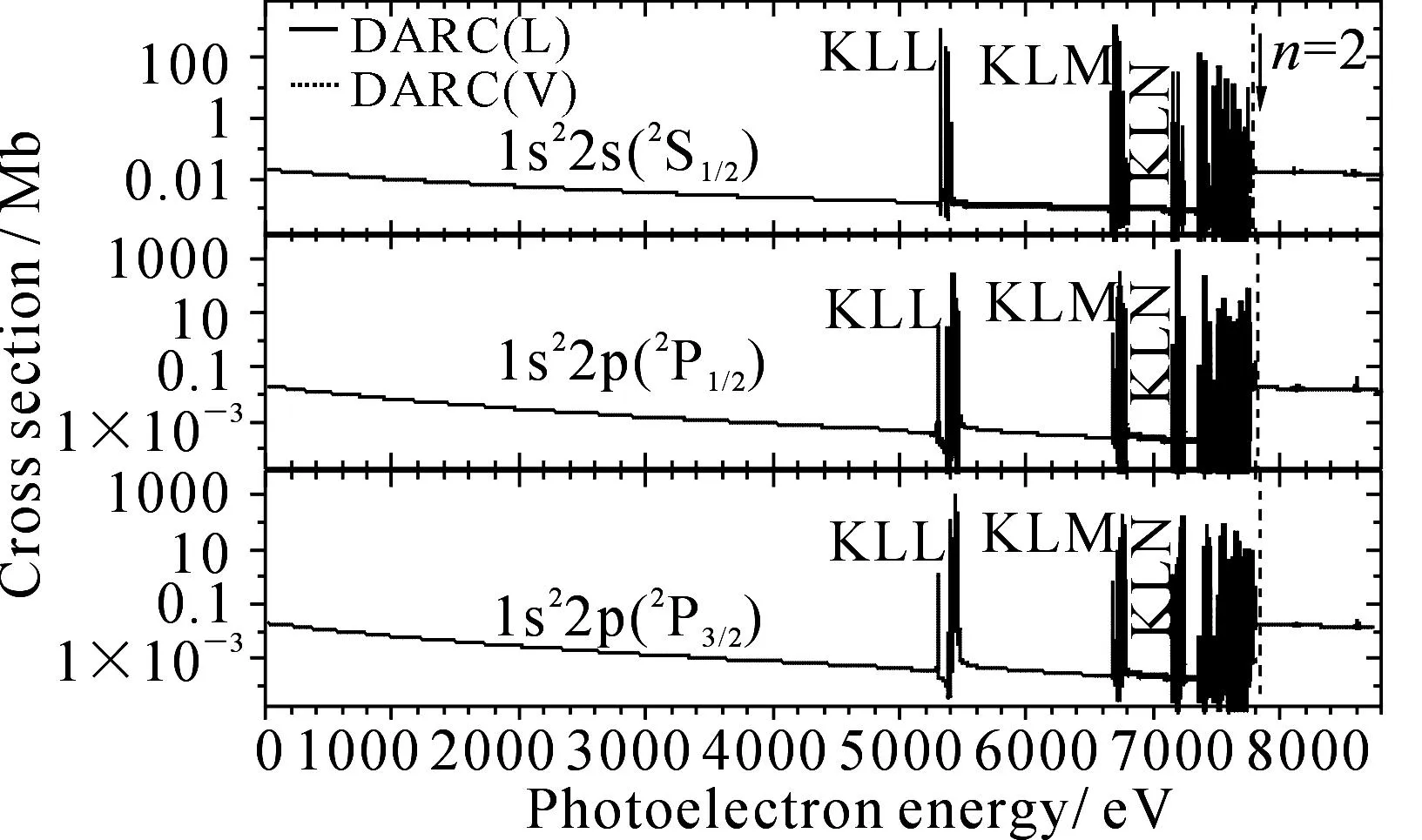
图1　Ni25+离子基态1s22s(2S1/2)及激发态

2结果与讨论

图2给出了利用DARC程序计算所得[Ni26+(1s21S0)+e-]J→Ni27+(1s22s2SJ′=1/2)+hν光复合过程分通道的截面及总截面(分通道截面的求和).根据对称性，在电偶极近似下，光复合初、末态的总角动量需满足ΔJ=J-J′=0,±1，其中J和J′分别对应光复合初态(靶离子+自由电子)及末态(N+1电子体系的束缚态)的总角动量量子数.从图中可以看出，目前计算所得长度规范(L)和速度规范(V)下光复合的截面一致性非常好.在KLL共振能区，对应通道J=1/2和J=3/2，分别有3条共振线，经分析它们分别来自中间双激发态[1s2s2p]J=1/2和[1s2s2p]J=3/2.作为对计算结果的检验，图2也给出了独立过程近似下利用基于MCDF理论的RATIP程序[28]计算所得RR过程的截面.不难看出目前MCDF理论的结果与R矩阵理论的光复合结果的背景截面吻合的很好.图3和图4分别给出了目前R矩阵理论计算的Ni26+(1s2)→Ni25+(1s22p2P1/2,2P3/2)光复合过程态分辨的分通道的截面和总截面，作为比较，图中同时给出了目前利用MCDF理论所得RR过程的截面.结果表明，在KLL能区，上述两个过程分别包含了6条和9条共振线，MCDF理论和R矩阵理论所得RR过程的截面普遍符合的很好，在5380~5460 eV能区的共振线附近出现的偏差，一定程度上反应了DR与RR过程间的干涉和重叠共振效应的影响.

图2　Ni26+离子1s21S0→1s22s 2S1/2光复合

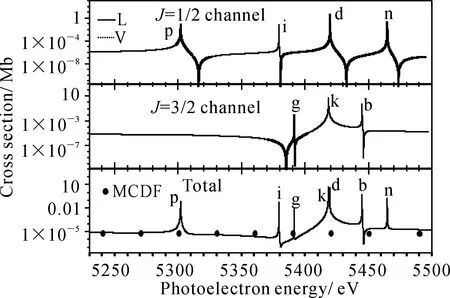
图3　Ni26+离子1s21S0→1s22p 2P1/2

为了对图1中KLL共振能区的共振峰(对应双电子伴线)进行标识和分析，本文利用基于相对论组态相互作用的FAC程序[25]对Ni25+离子涉及1s2s2,1s2s2p,1s2p2双激发组态的精细能级、辐射和Auger几率以及共振宽度等进行了计算，并在孤立共振近似下(见(8)式)得到了22条双电子伴线的强度，所得结果与R矩阵理论、Nahar等[27]

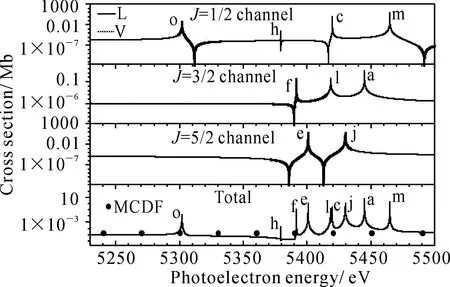
图4　Ni26+离子1s21S0→1s22p 2P3/2

表2Ni26+离子KLL共振能区双电子伴线的标记、对应的跃迁、共振能(eV)、

Auger和辐射几率(s-1)、共振态宽度(eV)以及伴线强度(×10-20cm2ev)

Tab 2The KLL resonances in electron-ion recombination of Ni26+correspond to the 22 dielectronic satellite lines.

The columns represent the key notation for a satellite line,the resonant transition,resonant energy in the present DARC and FAC calculations,and from BPRM[27]and NIST[30]results,the Auger decay probabilitiesAjfand radiative transition probabilitiesAji(s-1),resonant widthΓd(eV) and the satellite strength in 10-20cm2eV in the present work from the DARC and FAC calculations,and from BPRM results[27].

KeyTransitionEdi/eVAadfArdiDARCFACBPRM[27]NIST[30](×1013s-1)Γd/eVRS/(×10-20cm2eV)DARCFACBPRM[27]o1s2s2(2S1/2)→1s22p(2P3/2)5302.05293.85296.05294.115.351.220.11810.260.170.891.18*p1s2s2(2S1/2)→1s22p(2P1/2)5302.25293.85296.05294.115.351.350.11810.570.370.881.32*v1s2p(3p)2s(4P1/2)→1s22s(2S1/2)5314.05306.35312.35307.90.010.920.00620.040.00390.060.98*u1s2p(3p)2s(4P3/2)→1s22s(2S1/2)5320.65311.25321.35312.70.123.060.02097.390.070.163.21*r1s2p(1p)2s(2P1/2)→1s22s(2S1/2)5358.95352.05357.25351.24.7240.510.29808.341.353.8040.10*40.00†q1s2p(1p)2s(2P3/2)→1s22s(2S1/2)5373.45365.35372.25364.30.0566.130.43601.680.030.0864.60*i1s2p2(4P1/2)→1s22p(2P1/2)5379.65371.25397.45372.60.044.290.02860.070.010.084.62*

续表2

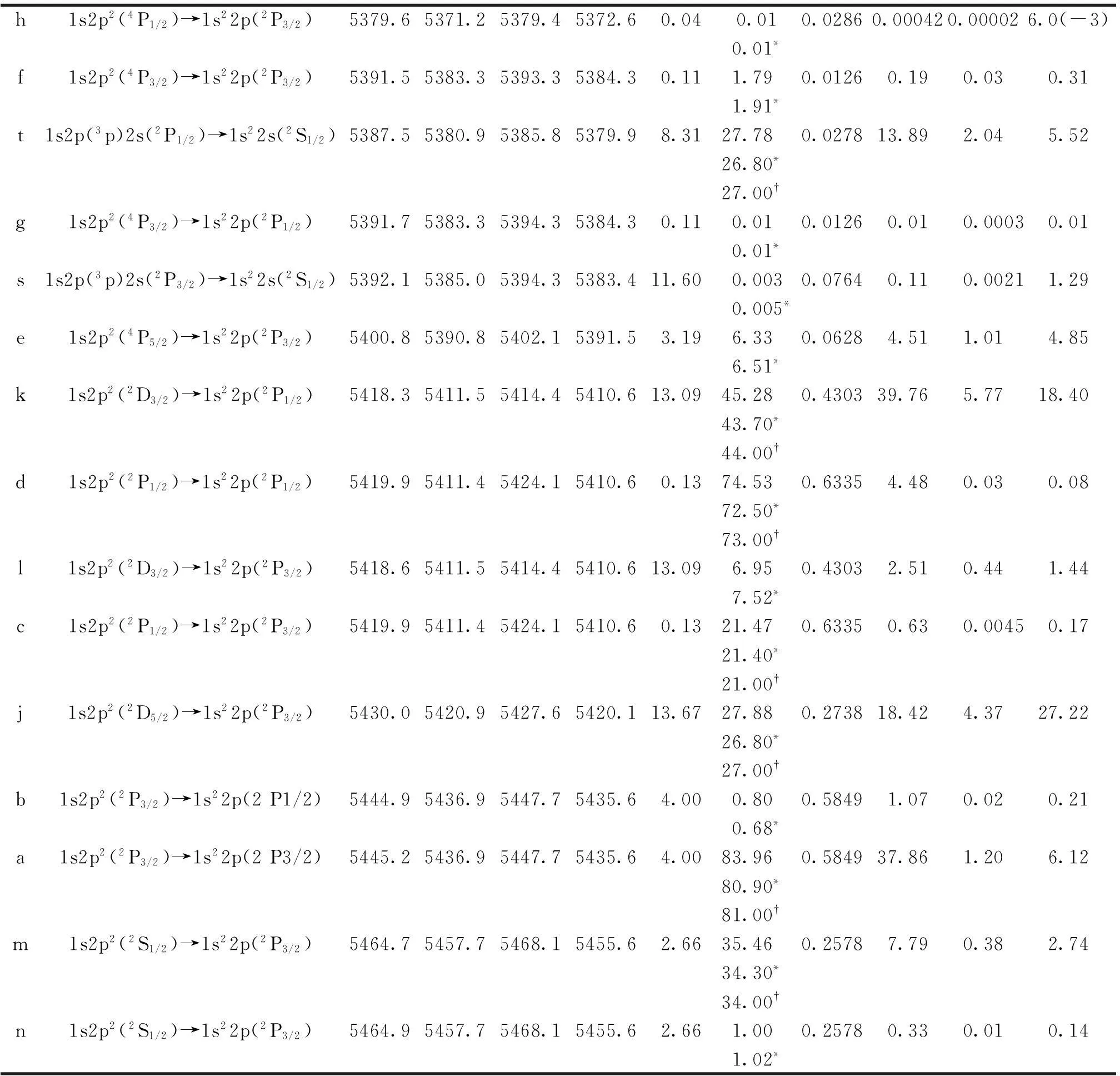
h1s2p2(4P1/2)→1s22p(2P3/2)5379.65371.25379.45372.60.040.010.02860.000420.000026.0(-3)0.01*f1s2p2(4P3/2)→1s22p(2P3/2)5391.55383.35393.35384.30.111.790.01260.190.030.311.91*t1s2p(3p)2s(2P1/2)→1s22s(2S1/2)5387.55380.95385.85379.98.3127.780.027813.892.045.5226.80*27.00†g1s2p2(4P3/2)→1s22p(2P1/2)5391.75383.35394.35384.30.110.010.01260.010.00030.010.01*s1s2p(3p)2s(2P3/2)→1s22s(2S1/2)5392.15385.05394.35383.411.600.0030.07640.110.00211.290.005*e1s2p2(4P5/2)→1s22p(2P3/2)5400.85390.85402.15391.53.196.330.06284.511.014.856.51*k1s2p2(2D3/2)→1s22p(2P1/2)5418.35411.55414.45410.613.0945.280.430339.765.7718.4043.70*44.00†d1s2p2(2P1/2)→1s22p(2P1/2)5419.95411.45424.15410.60.1374.530.63354.480.030.0872.50*73.00†l1s2p2(2D3/2)→1s22p(2P3/2)5418.65411.55414.45410.613.096.950.43032.510.441.447.52*c1s2p2(2P1/2)→1s22p(2P3/2)5419.95411.45424.15410.60.1321.470.63350.630.00450.1721.40*21.00†j1s2p2(2D5/2)→1s22p(2P3/2)5430.05420.95427.65420.113.6727.880.273818.424.3727.2226.80*27.00†b1s2p2(2P3/2)→1s22p(2P1/2)5444.95436.95447.75435.64.000.800.58491.070.020.210.68*a1s2p2(2P3/2)→1s22p(2P3/2)5445.25436.95447.75435.64.0083.960.584937.861.206.1280.90*81.00†m1s2p2(2S1/2)→1s22p(2P3/2)5464.75457.75468.15455.62.6635.460.25787.790.382.7434.30*34.00†n1s2p2(2S1/2)→1s22p(2P3/2)5464.95457.75468.15455.62.661.000.25780.330.010.141.02*

Note:*Ref[33],†Ref[30].

图5(a)为KLL共振能区附近Ni26+(1s2)离子光复合过程的总截面，图5(b)为利用FAC计算所得22条双电子伴线的位置和强度.为了与Kannp等[34]EBIT实验测量的KLL双电子复合过程的实验结果进行比较，我们分别对DRAC和FAC计算的双电子伴线强度进行了Gauss卷积(FWHM=54 eV)，所得结果与实验结果[34]见图5(c)，其中，为了消除由于Breit相互作用引起的共振能的偏差，DARC的结果均向左平移了12 eV.从图中可以看出，目前理论KLL伴线的位置和线型与实验结果整体符合较好，在5 230~5 460 eV能区，DARC结果略高于实验结果.在5 460~5 550 eV能区实验结果普遍高于理论结果，其主要原因是实验测量中还观测到了其他电荷态Ni离子的贡献[34]由于实验的分辨率(54 eV)仍然比较低，不能对单个的共振峰进行分辨，所以目前理论中所展现的DR和RR之间的干涉效应不能在实验结果中被观测到.

3结论

利用基于相对论R矩阵的理论方法，系统研究了Ni26+离子在 KLL能区附近的光复合截面，并对其中的共振峰进行了标识和分析，所得双电子复合过程的伴线强度与FAC程序计算的结果以及其他理论和实验结果进行了比较.结果表明,① 目前基于相对论R矩阵的DARC程序可以被用来获得高电荷态离子精细的态分辨光复合截面，其中辐射复合和双电子复合过程之间的干涉和重要的重叠共振的贡献能被自动考虑；② Breit相互作用对高电荷态离子靶态及共振态的能级有重要影响，辐射阻尼效应通常会降低双电子伴线的强度，在以后的研究中需要对这两种效应系统考虑；③ 目前相对论R矩阵理论和孤立共振近似下计算所得双电子复合过程的结果与EBIT的实验测量结果整体符合比较好，但对于其中的干涉效应需要更精细的实验来观测.

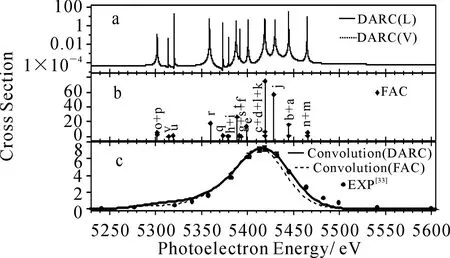
图5(a)Ni26+离子KLL共振能区附近总光复合截面；(b)FAC计算的双电子伴线的位置和强度；(c)理论卷积(FWHM=54 eV)所得双电子伴线相对强度与实验结果的比较.虚线：DARC的结果;实线： FAC的结果;黑色圆点：Kannp等EBIT实验结果[34]

Fig 5(a)The total photorecombination cross section of Ni26+ion nearby KLL energy;(b)Resonant position and strength from FAC calculations;(c)The relative strength of the resonance lines convoluted by use a Gaussian profile of FWHM=50 eV compare to the EBIT results from Kannp et al.[34]The red dotted line shows the rsults of DARC;the black line shows the results of FAC;the black circle with errors show the EBIT results[34].

参考文献:

[1]BEIERSDORFER P,PHILLIPS T W,WONG K L,et al.Vogel.Measurement of level-specific dielectronic-recombination cross section of heliumlike Fe XXV[J].PhysRevA,1992,46:3812-3820.

[2]DAVIES P C W,SEATON M J.Radiation damping in the optical continuum[J].JPhysB,1969,2:757-767.

[3]BEL R H,SEATON M J.Dielectronic recombination.I.General theory[J].JPhysB,1985,18:1589-1629.

[4]JACOBS V,COOPER J,HAAN S.Unified description of radiative and dielectronic recombination,including the coupling between autoionization and radiation continua[J].PhysRevA,1987,36:1093-1113.

[5]HAAN S,JACOBS V.Projection-operator approach to the unified treatment of radiative and dielectronic recombination[J].PhysRevA,1989,40:80-94.

[6]MITNIK D M,PINDZOLA M S,BADNELL N R.Total and partial recombination cross section for F6+[J].PhysRevA,1999,59:3592-3605.

[7]NAHAR S,PRADHAN A.Photoionization and electron-ion recombination:The carbon sequence[J].PhysRevA,1991,44:2935-2948.

[8]NAHAR S,PRADHAN A.Electron-ion recombination in the close-coupling approximation[J].PhysRevLett,1992,68:1488-1491.

[9]NAHAR S,PRADHAN A.Unified treatment of electron-ion recombination in the close-coupling approximation[J].PhysRevA,1994,49:1816-1835.

[10]KNAPP D,BEIERSDORFER P,CHEN M,et al.Observation of interference between dielectronic recombination and radiative recombination in highly charged uranium ions[J].PhysRevLett,1995,74:54-57.

[11]GORCZYCA T W,ROBICHEAUX F,PINDZOLA M S,et al.Comparisons between perturbative and radiation-damped R-matrix approaches to dielectronic recombination:Application to Ar15+[J].PhysRevA,1996,54:2107-2115.

[12]PINDZOL A M,ROBICHEAUX F,BADNELL N,et al.Photorecombination of highly charged uranium ions[J].PhysRevA,1995,52:420-425.

[13]WANG J G,ZOU Y,DONG C Z,et al.Theoretical calculation of dielectronic-recombination cross section for hydrogen-like argon[J].ChinPhysLett,1995,12:530.

[14]TOBIYAMA H,NOHARA H,KAVANAGH A P,et al.Interference between dielectronic and radiative recombination in electron - highly charged Bi collisions[J].Physics:ConferenceSeries,2007,58:239-242.

[15]MCLAUGHLIN D J,HAHN Y,TAKACS E,et al.Radiative and inner-shell dielectronic recombination in a highly charged barium ion[J].PhysRevA,1996,54:2040-2051.

[16]HEMMERS O,FISHER G,GLANS P,et al.Beyond the dipole approximation:angular-distribution effects in valence photoemission[J].JPhysB,1997,30:L727-L733.

[17]MANNERVIK S,ASP S,DEWITT D R,et al.Spectroscopic study of lithiumlike carbon by dielectronic recombination of a stored ion beam[J].PhysRevA,1997,55:1810-1821.

[18]PRADHAN A K,ZHANG H L.Radiation damping of autoionizing resonances[J].JPhysB,1997,30:L571-L580.

[19]ZIMMERMANN M,GRÜN N,SCHEID W.Photo recombination on highly charged few-electron uranium ions[J].JPhysB,1997,30:5259-5270.

[20]BRAUN J,BRENNER G,BRUHNS H,et al.State-selective quantum interference observed in the recombination of highly charged Hg75+…78+mercury ions in an electron beam ion trap[J].PhysRevLett,2005,94:230-240.

[21]NAKAMURA N,KAVANAGH A.Asymmetric profiles observed in the recombination of Bi79+:A benchmark for relativistic theories involving interference[J].PhysRevA,2009,80:979-981.

[22]BEHAR E,JACOBS V L,OREG J,et al.Measure for the effect of quantum interference between radiative and dielectronic recombination[J].PhyRevA,2000,62:1201-1210.

[23]GORCZYCA T W,FELFLI Z,DEB N C,et al.Inner-shell photoabsorption of Fe14+:Unimportance of correlation and relativistic effects[J].PhysRevA,2000,63:785-795.

[24]NORRINGTON P H.2004,www.am.qub.ac.uk/DARC.

[25]GU M F.Indirect X-ray line-formation processes in iron L-shell ions[J].AstrophysJ,2003,582:1251-1250.

[26]GAO L C,ZHANG D H,XIE L Y,et al.Theoretical study of the photoionization process of Ne-like Ar,Fe,Kr and Xe ions[J].JPhyB,2013,46:1-10.

[27]NAHAR S N,PRADHAN A K.Dielectronic satellite spectra of heliumlike iron and nickel from the unified recombination method[J].PhysRevA,2006,73:1-8.

[28]FRITASCHE S.The RATIP program for relativistic calculations of atomic transition,ionization and recombination properties[J].ComputPhysCommun,2012,183:1525-1559.

[29]JONSSON P,HE X,FISCHER C F,et al.The grasp 2 K relativistic atomic structure package[J].ComputPhysCommun,2007,177:597-622.

[30]KRAMIDA A,RALCHENKO Y,READER J,et al.National Institute of Standards and Technology.NIST.2014,NIST Atomic Spectra Database(version 5.2),http://physics.nist.gov/asd.

[31]FANO U,COOPER J W.Spectral distribution of atomic oscillator strengths[J].RevModPhys,1968,40:441-507.

[32]O’ROURKEL B E,KURAMOTO H,LI Y M,et al.Dielectronic recombination in He-like titanium ions[J].JPhyB,2004,37:2342-2353.

[33]HATA J,GRANT I P.Wavelengths and radiative transition rates for selected lines of 2-,3- and 4-electron systems for the elements from Ca to Cu[J].MonNotRAstroSoc,1984,211:549-557.

[34]KNAPP D A,MARRS R E,LEVINE M A,et al.Dielectronic recombination of heliumlike nickel[J].PhysRevLett,1989,62:2104-2107.

(责任编辑孙对兄)

The relativistic R-matrix study for level-specific

photorecombination cross sections of Ni26+ion

XIE Lu-you,MA Chi,MA Kun,DONG Chen-zhong,ZHANG Deng-hong

(Key Laboratory of Atomic and Molecular Physics & Functional Materials of Gansu Province,

College of Physics and Electronic Engineering,Northwest Normal University,Lanzhou 730070,Gansu,China)

Abstract:In this study,photoionization cross sections are calculated for the ground level 1s22s(2S1/2)and the excited levels 1s22p(2P1/2,2P3/2) of Ni25+ion using the Dirac atomic R-matrix codes(DARC) based on the relativistic R-matrix method.The unified level-specific photorecombination(i.e.radiative recombination and dielectronic recombination) cross sections of the ground state Ni26+(1s2) iron are obtained through the detailed balance principle.Detailed calculations exhibit interference effects in resonance profiles.To identify and analyze the locations and strengths for all resonant peaks,detailed calculations are performed for all known KLL resonant states by use the Flexible atomic code(FAC) based on the relativity configuration interaction(RCI) method,the resonant energies and strengths together with radiative and Auger transition rates,and the resonant width are listed.The obtained dielectronic satellite energies and strengths from DARC and FAC calculations are compared with earlier theoretic and experimental works and significant differences and similarities are discussed.

Key words:photorecombination cross sections;relativistic R-matrix method;resonant energy;resonant strength

中图分类号：O 562.6

文献标志码：A

文章编号：1001-988Ⅹ(2015)02-0024-08

作者简介：颉录有(1975—)，男，甘肃武山人，副教授，博士，硕士研究生导师.主要研究方向为原子结构与原子碰撞.E-mail:xiely@nwnu.edu.cn

基金项目:国家自然科学基金资助项目(U1331122,U1332206,11274254，11464042)

收稿日期：2014-10-18;修改稿收到日期:2015-01-04