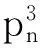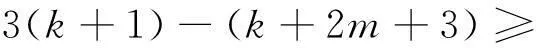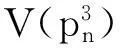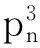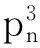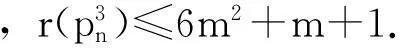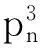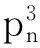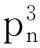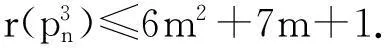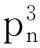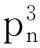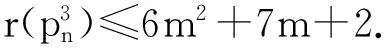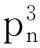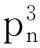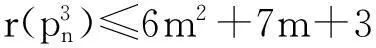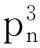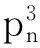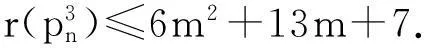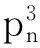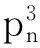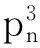立方路的多级距离数

郭红芳，左连翠*

(天津师范大学数学科学学院，天津　300387)

立方路的多级距离数

郭红芳，左连翠*

(天津师范大学数学科学学院，天津300387)

摘要：连通图G的多级距离标号(电台标号)是顶点集V(G)到非负整数集{0,1,2,…}的一个映射f，使得对于任意的u,v∈V(G)满足：≥diam(G)+1-d(u,v)，其中diam(G)是图G的直径，d(u,v)表示两点u,v之间的距离．映射f的跨度是指{f(u)-f(v)}．图G的多级距离数是指图G的所有多级距离标号的最小跨度．图G的立方是由图G通过在距离不超过3的任两点间添加一条连边构成．本文给出了立方路的多级距离数．

关键词：多级距离数；多级距离标号；有效频道分配；最小跨度；立方路

0引言

多级距离标号又称电台标号，它是2-距离标号(L(2,1)-标号)的拓展．无论是L(2,1)-标号还是多级距离标号，都源于Hale的无线电频道分配问题，它们都是特殊的染色问题．给定一个电台的集合，一个有效的频道分配是指这样一个函数，它分配给每一个电台一个频道，使这些电台之间的信号避免相互干扰．电台之间相互干扰的度(级别)与电台所处的位置有关，即两电台之间的距离越近，它们相互干扰的度就越大．因此为了避免这种干扰，距离越近的电台，它们之间的频道差就应该越大，从而频道差由两电台之间的距离决定．为了模拟这个问题，图论学家们构造了一个图，把每一个电台表示成图的一个顶点，每一对相邻的电台在图中相应点之间连一边．由此频道分配问题即可转化成图的点染色问题．

图G的多级距离数是指图G的所有多级距离标号的最小跨度，记为r(G)．

图G的立方，是指图G通过在所有距离不超过3的两个顶点之间添加一条连边得到，记为G3．我们称一条路(或圈)的立方为立方路(或立方圈)．随着路和圈的多级距离数的完全解决，以及平方路的多级距离数被完全解决，我们考虑立方路的多级距离数，并得出下面的结论．

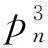
1主要定理的证明

本文用pn表示具有n个顶点的一条路，其中V(pn)={v1,v2,…,vn}和E(pn)={vivi+1:i=1,2,…,n-1},显然

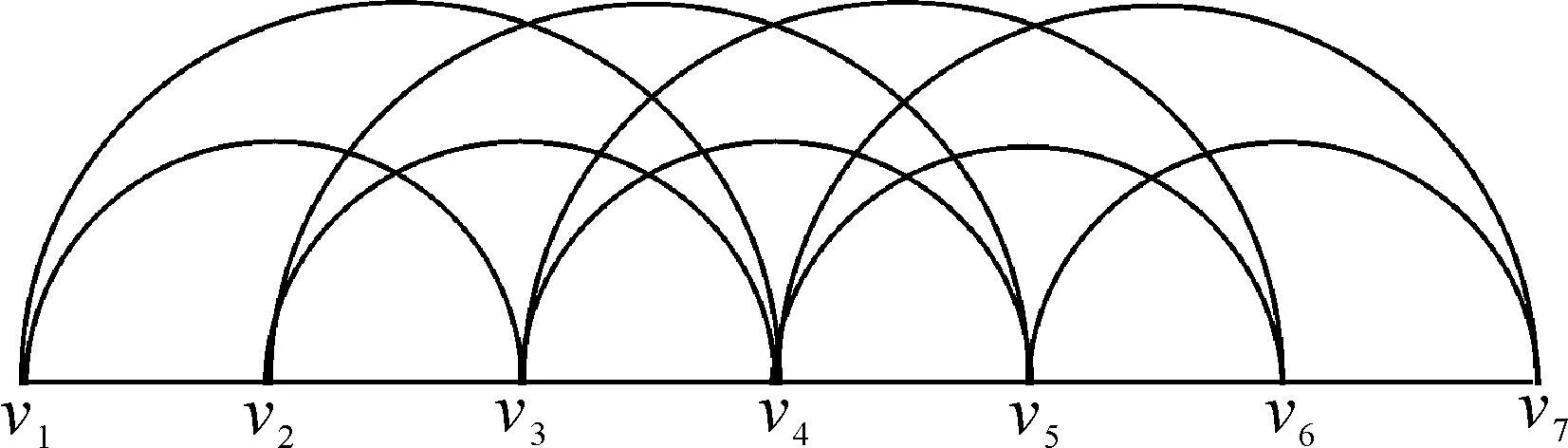
图1　具有7个顶点的立方路

1.1下界

首先证明定理1中的下界．pn的中间顶点定义为路pn的中心．一条奇路p2k+1只有一个中心vk+1，而一条偶路p2k有两个中心vk和vk+1，本文中取vk为偶路的中心．对于任意一个顶点u∈V(pn)，u的距离是指在pn中由u到pn的中心点的最短距离，记为L(u)．比如，设n=2k+1，则L(v1)=k,L(vk+1)=0，顶点序列A的距离记为L(A)．如果n=2k+1，则

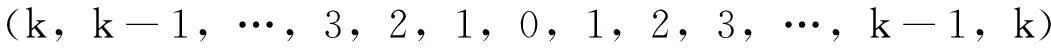
如果n=2k，则

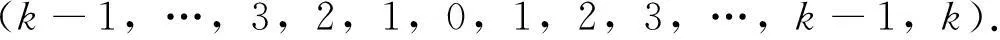
按如下方式定义左、右顶点集：如果n=2k+1，则左、右顶点集分别为{v1,v2,…,vk,vk+1}和{vk+1,vk+2,…,v2k,v2k+1}.

注意此时中心点vk+1既属于左顶点集又属于右顶点集．如果n=2k，则左、右顶点集分别为{v1,v2,…,vk-1,vk}和{vk+1,vk+2,…,v2k-1,v2k}.如果两个点都属于右(或左)顶点集，则称它们在同一边；否则，称它们在不同边．

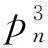
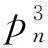
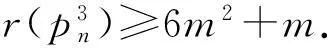
把这n-1个不等式相加，得到

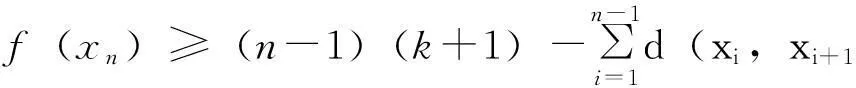
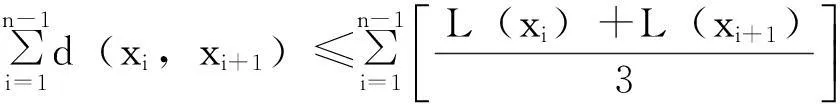
观察上面的不等式可得：

(i)对每个i，有

等号成立当且仅当xi和xi+1在pn的不同边，除非它们其中之一是中心点.

(ii)(2)式右边的求和项中，L(x1)和L(xn)仅出现一次，其余各项均出现两次．注意到

那么存在3m-1个i(1≤i≤6m-1)满足

以及3m个i(1≤i≤6m-1)满足

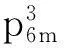
在上述排列中，当i(1≤i≤6m-1)为偶数时,有

当i(1≤i≤6m-1)为奇数时,有

另外，所有顶点中只有中心点的距离为0，从而

其中L(x1)=0,L(xn)=1.因此，由(1)式可得

2)当n=6m+1时，直径k=2m，由于

与(1)式类似可得

其中L(x1)=0,L(xn)=1.因此由(1)式可得

3)当n=6m+2时，直径k=2m+1.由于

其中L(x1)=0,L(xn)=1,因此由(1)式可得

4)当n=6m+3时，直径k=2m+1.由于

其中L(x1)=0,L(xn)=1,故由(1)式得

5)当n=6m+4时，直径k=2m+1.由于

其中L(x1)=0,L(xn)=1,结合(1)式可得

(6m2+11m+3)=6m2+7m+3.

6)当n=6m+5时，直径k=2m+2.由于

其中L(x1)=0,L(xn)=1,故由(2)式得

1.2上界

只要给出跨度为上述值的多级距离标号，即可证明定理1．首先，证明下面的引理．

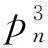
(3)

证明实际上，

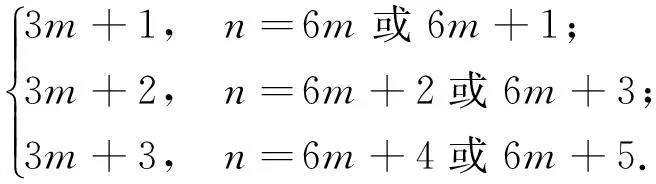
设f是满足上述假设的一个函数，只要证明：对任意的j≥i+2，有

对于i=1,2,…,n-1，设fi=f(xi+1)-f(xi)，则对于任意的j≥i+2，有

不妨设d1(xi,xi+1)≥d1(xi+1,xi+2)(对于d1(xi+1,xi+2)≥d1(xi,xi+1)的情况可以类似的证明)，则有d(xi,xi+1)≥d(xi+1,xi+2)，且

下面分情况进行讨论．

1)假设j=i+2，设xi=va,xi+1=vb,xi+2=vc，只要考虑下面的情形：

( i )b

此时必有d(xi,xi+1)≤d(xi+1,xi+2)，但已知d(xi,xi+1)≥d(xi+1,xi+2)，所以

从而d1(xi,xi+1)<3,故d(xi,xi+2)=1，因此

( ii )a

那么

(iii)a

易知d(xi,xi+2)≥d(xi,xi+1)-d(xi+1,xi+2).当n≡2,3,4,5(mod6)时，易证

当n≡0,1(mod6)时，若

则有d(xi+1,xi+2)≤m，那么

若

则由(3)式得知d1(xi,xi+1)≡2(mod3)，因此

从而

2)假设j=i+3．

首先假设d(xi,xi+1),d(xi+1,xi+2),d(xi+2,xi+3)中至少有一对的和至多为2m+3，则

其次，假设d(xi,xi+1),d(xi+1,xi+2),d(xi+2,xi+3)中每一对的和都大于2m+3，则显然有

(4)

设xi=va,xi+1=vb,xi+2=vc,xi+3=vd．由(4)式，一定有a

从而由(3)式可得

3)设j≥i+4．

显然min{d1(xi,xi+1),d1(xi+1,xi+2)}≤φ(n),且对任意1≤i≤n-1，有fi=k+1-d(xi,xi+1)．

当n≡2,3,4(mod6)时，有

因此，

当n≡5(mod6)时，有

因此，

当n≡0,1(mod6)时，有

因此，

综上所述，引理4得证．】

当m为奇数时，顶点排列如下：

当m为奇数时，顶点排列如下：

r(f)=6m2+7m+1.

当m为奇数时，顶点排列如下：

当m为奇数时，顶点排列如下：

综上所述，定理1得证．

参考文献:

[1]CHANGG,KEC,KUOD,etal．Ageneralizeddistancetwolabelingofgraphs[J].Disc Math,2000,220:57-66.

[2]CHANGG,KUOD.TheL(2,1)-labelingproblemongraphs[J].SIAM J Disc Math,1996,9:309-316.

[3]CHARTRANDG,ERWIND,HARARYF,etal.Radiolabelingsofgraphs[J].Bull Inst Combin Appl,2001,33:77-85.

[4]CHARTRANDG,ERWIND,ZHANGP.AgraphlabelingproblemsuggestedbyFMchannelrestrictions[J].Bull Inst Combin Appl,2005,43:43-57.

[5]GEORGESJ,MAUROD.Generalizedvertexlabelingswithaconditionatdistancetwo[J].Congr Numer,1995,109:141-159.

[6]GEORGESJ,MAUROD,STEINM.Labelingproductsofcompletegraphswithaconditionatdistancetwo[J].SIAM J Discrete Math,2001,14:28-35.

[7]GEORGESJ,MAUROD,WHITTLESEYM.Onthesizeofgraphslabeledwithaconditionatdistancetwo[J].J Graph Theory,1996,22:47-57.

[8]GEORGESJ,MAUROD,WHITTLESEYM.Relatingpathcoveringtovertexlabelingswithaconditionatdistancetwo[J].Disc Math,1994,135:103-111.

[9]GRIGGSJR,YEHRK.Labelinggraphswithaconditionatdistance2[J].SIAM J Disc Math,1992,5:586-595.

[10]CHARTRANDG,ERWIND,ZHANGP.Radioantipodalcoloringsofcycles[J].Congr Numer,2000,144:129-141.

[11]LIUD.Radio Number for Spiders[R].Manuscript,2004.

[12]LIUD,XIEM.Radio Number for Square Paths[R].Manuscript,2004.

[13]HALEWK.Frequencyassignment:theoryandapplications[J].Proc IEEE,1980,68:1497-1514.

[15]NIVENI,ZUCKERMANH,MONTGOMERYH.An Introduction to the Theory of Numbers[M].5thed.NewYork：JohnWileyandSonsInc,1991.

[16]GROSSJ,YELLENJ.Graph Theory and its Application[M].NewYork:CRCPress,1999.

[17]XIEM.Multiple Level Distance Labellings and Radio Number for Square Paths and Square Cycles[D].California:CaliforniaStateUniversity,2004.

[18]ZHAGNP.Radiolabellingsofcycles[J].Ars Combin,2002,65:21-32.

(责任编辑马宇鸿)

*通讯联系人，教授，博士，硕士研究生导师.主要研究方向为图论及其应用.E-mail:lczuo@163.com

The multi-level distance number for cubic paths

GUO Hong-fang,ZUO Lian-cui

(College of Mathematical Science,Tianjin Normal University,Tianjin 300387,China)

Abstract:The multi-level distance labeling for a connected graph G,also called the radio labeling,is a mapping {0,1,2,…} such that for any u,v∈V(G)≥diam(G)+1-d(u,v),where diam(G) is the diameter of G,and d(u,v) denote the distance between u and v in G.The span of f is defined as {f(u)-f(v)}.The multi-level distance number of a graph G is the minimum span of all multi-level distance labeling for G.The cubic of G is a graph constructed from G by adding edges between vertices of distance at most three parts in G.In this paper,the multi-level distance number for the cubic path is obtained.

Key words:multi-level distance number;multi-level distance labeling;valid radio channel assignment;minimum span;cubic path

中图分类号：O 157.5

文献标志码：A

文章编号：1001-988Ⅹ(2015)02-0012-07

作者简介：郭红芳(1990—)，女，河北临漳人，硕士研究生.主要研究方向为图论及其应用.E-mail:ghfkeji@126.com

基金项目:国家自然科学青年基金资助项目(61103073)

收稿日期：2014-03-12;修改稿收到日期:2014-07-13