静止边界法在永磁同步发电机旋转磁场及铁心损耗计算中的应用

郭健， 刘闯， 李凯琪

(南京航空航天大学自动化学院，江苏南京210016)

0 引言

有限元法是计算永磁同步发电机铁心损耗分布的有效途径之一［1－2］。而铁耗的计算又是以转子对应不同位置磁场分布(旋转磁场分布)的计算为基础，然后再根据电机求解区域磁密的时域波形和铁耗模型，进一步计算得到损耗分布及总损耗的大小。

目前，对于旋转磁场分布的计算一般都是采用模型重构的方法［3－6］，即通过建立转子处于不同位置时的有限元磁场模型来实现，其基本的求解流程如图1所示。可以看出，这种方法对于每一个转子位置的磁场分析都需要重复经历建模－划分网格－加载激励和边界－求解的过程，若所分析电机的结构较复杂时，其反复的建模将使得整个分析过程效率低下。同时，由于定子铁耗计算的基础是单元磁密的时域波形，但是模型重构法在计算每个时刻磁场时(即转子处于不同位置)都要重新建模－网格划分，这将导致单元的形状、大小及节点信息都有可能发生变化，而每个时刻得到的磁场结果都会由于下一个时刻重构模型后单元信息的变更而无法保存，这就给定子铁耗的准确计算带来了困难［7－9］。

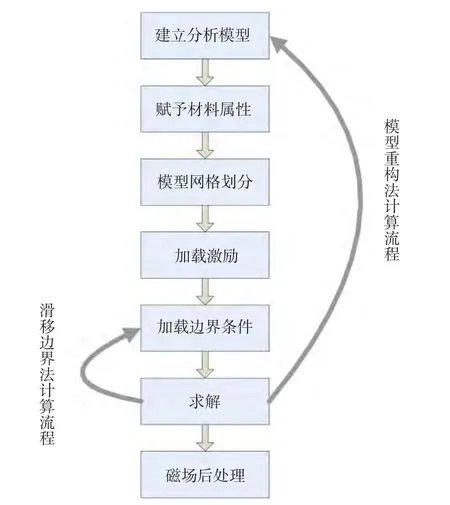
图1 转子旋转过程中磁场计算流程Fig.1 Calculation flow in the process of rotor rotation

针对模型重构法存在的问题，文献［10－11］提出一种处理电磁场有限元运动问题的新方法－运动边界法。在该方法中，沿电机气隙的中心线画两条完全重合的圆弧，将气隙一分为二，它们分别属于定子和转子。对定子和转子采用两套相对独立的坐标系，定子坐标系固定在定子上，不转动。转子坐标系固定在转子上，并将随转子同步转动。由于运动边界法不需要在计算过程中不断地对有限元网格进行调整，因此，计算的效率得到了提高，同时也为铁耗准确计算提供了可能。本文将在文献［10－11］的基础上，将运动边界法中转子的运动坐标系统一到定子的静止坐标下，进一步简化旋转磁场计算的前处理过程。以静态边界取代动态边界的本质是定子、转子都固定不动，转子的旋转仅通过边界节点磁位耦合的顺序来等效，从而使得计算效率进一步提高。通过对电机磁力线及磁密分布的计算，证明了本文方法的有效性和高效率。同时本文还对静止边界法在永磁同步发电机铁耗计算中的应用进行了研究。

1 静止边界法

1.1 电机磁场计算的有限元模型

对于轴向对称的永磁同步发电机，忽略定子铁心涡流弱磁作用，电机内的磁场可简化为二维静态磁场来分析。若采用矢量磁位法，求解电机二维静磁场的边值问题为:

式中:Az为矢量磁位;Jz为电流密度矢量;v为磁阻率。

1.2 静止边界条件引入

静止边界即将整个电机模型从定、转子间气隙中心线割成两个独立的部分进行建模和划分网格，定子部分的内边界与转子部分的外边界在分割线位置重合、但不共线，如图2所示。模型建好后，定、转子模型就固定不动，转子的旋转只要通过改变定子内边界与转子外边界上对应节点的磁位耦合顺序来等效，从而实现了转子、定子坐标系的统一。

在保证旋转磁场及气隙磁场准确计算的前提下，边界节点的数量需根据电机槽、齿的数量进行调整。为了方便理解静止边界法，本文以360个节点为例进行介绍，其它节点数量的处理方式以此类推。如图3中，若转子的旋转速度为V(度/秒)，静止边界线上的节点为360个(定子、转子边界线各360个节点，且相邻节点间等间距，间距为1度。)，在t=0时刻，通过将(r0，s0)、(r1，s1)…(r359，s359)对应节点的磁位Az进行耦合即可得到转子初始位置的磁场分布，耦合方程如式(2)。

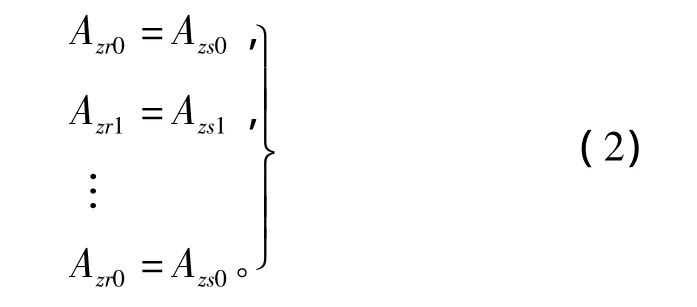
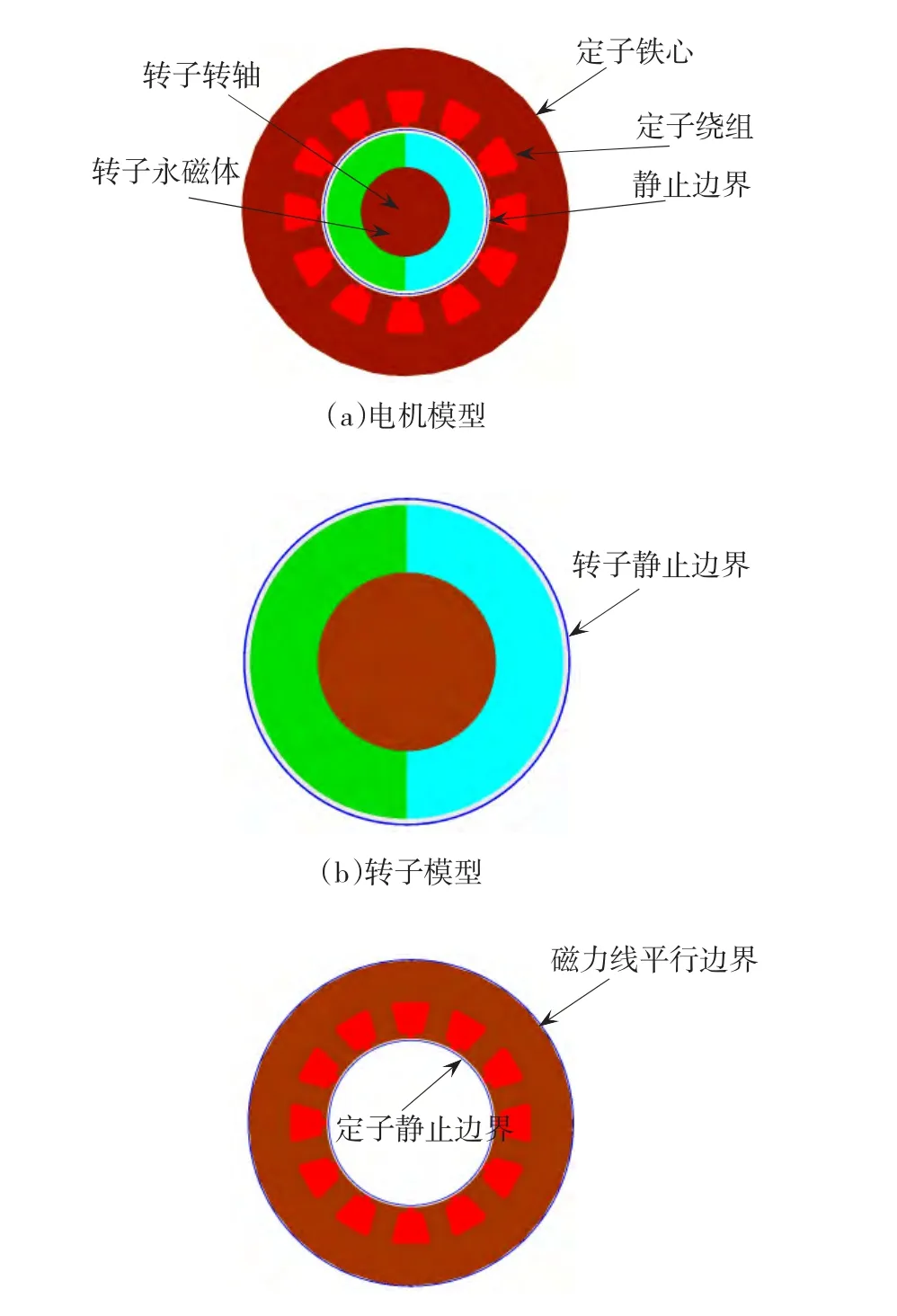
图2 静止边界模型Fig.2 The stationary boundary model

在 t=45°/V 时刻将(r45，s0)、(r46，s1)…(r89，s44)、(r90，s45)…(r44，s359)对应节点的磁位进行耦合(如图3(b)所示)，即可得到转子旋转45°位置的磁场分布;在 t=90°/V 时刻，将(r90，s0)、(r91，s1)…(r359，s269)、(r0，s270)…(r89，s359)对应节点的磁位进行耦合即可得到转子旋转90°位置的磁场分布，耦合方程如式(3);以此类推即可得到转子旋转一周在电机中各位置产生的旋转磁场波形。

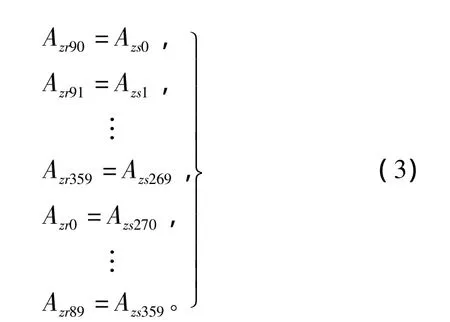
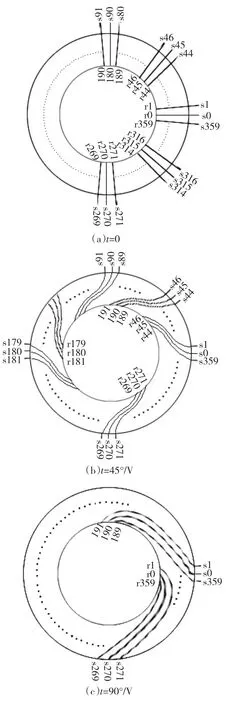
图3 转子不同位置时静止边界线上的节点耦合Fig.3 Stationary boundary node’s coupling order corresponding to the positions of rotor

静止边界法通过边界节点的磁位耦合顺序来等效转子的位置及旋转，磁场分析的效率大大提高，其对应的求解流程如图1所示;同时静止边界条件的引入因为不需要重构模型，从而保证了单元的标号、形状及位置都不会随着转子的等效旋转而发生改变，这就为准确计算铁心单元磁场时域解提供可能，同时也为后续铁心损耗分布的准确计算及温度场计算时候分布热源的耦合加载提供了便利的条件。

2 静止边界法验证

2.1 验证模型

本文以一台500 W/100 000 r/min的高转速永磁发电机为例，进行静止边界法的有效性验证，验证模型的拓扑结构如图2(a)所示，模型对应的参数如表1所示。

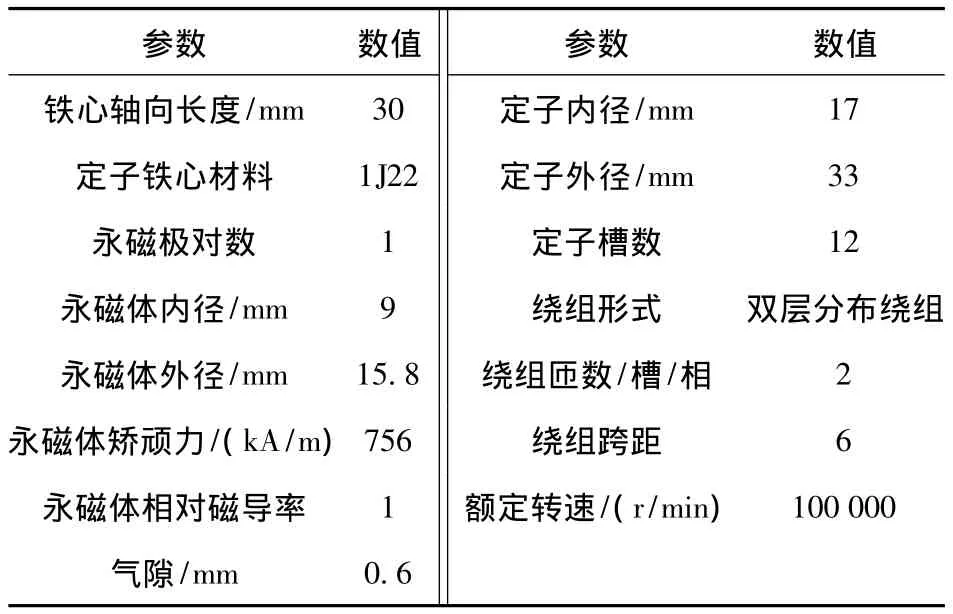
表1 模型参数Table 1 Model parameters

2.2 静止边界法对转子旋转的等效

针对表1模型参数，分别采用模型重构法和静止边界法对电机空载状态下的旋转磁场分布进行计算，计算结果如图4所示。可以看出，两种方法得到的定子中磁场分布一致。对于静止边界法，定子中的磁场会随着节点耦合顺序的改变而发生旋转，具有与模型重构法同样的效果，证明了静止边界法模拟转子旋转过程的有效性。

某一时刻电机空载磁场的分布主要取决于转子的位置，其与转子转速并无直接的关系。即转子处于某一位置时(如图4所示的4个转子位置)，无论转子转速是多少，其空间磁场的分布应该不变。按此思路可以计算得到转子转到不同位置角θ时的磁位 A(θ)和磁密 B(θ)的数值。

转子转速为n转/分时，转子转动θ角度所经历的时间为

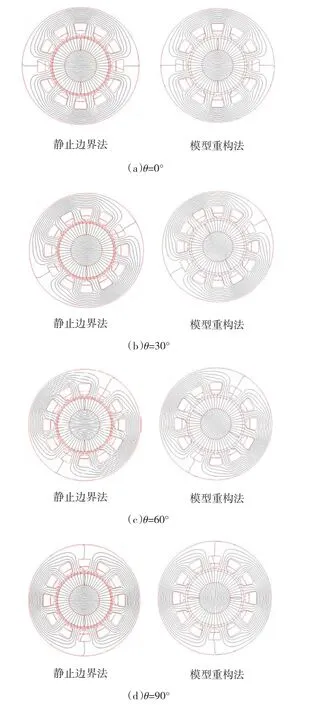
图4 两种方法的磁力线分布比较Fig.4 Comparison of two methods on magnetie field distribution

由此可以变换得到不同时刻对应的时间域磁位A(t)和磁密B(t)数值。

按照图1所示的求解流程，转子旋转过程中磁场计算是实现不同位置角θ时的磁位A(θ)和磁密B(θ)的分布计算，而磁场计算的后处理阶段，则根据电机的实际转速，将磁位A(θ)和磁密B(θ)转换为时间域磁位A(t)和磁密B(t)。然后再进一步计算发电机的感应电动势、损耗或者温升等性能参数。

2.3 静止边界法磁密计算结果验证

图5为转子旋转90°时对应的磁密分布，可以看出两种方法计算的结果一致，最大磁密出现在定子铁心的轭部，证明了静止边界法对电机磁密分布计算的准确性。

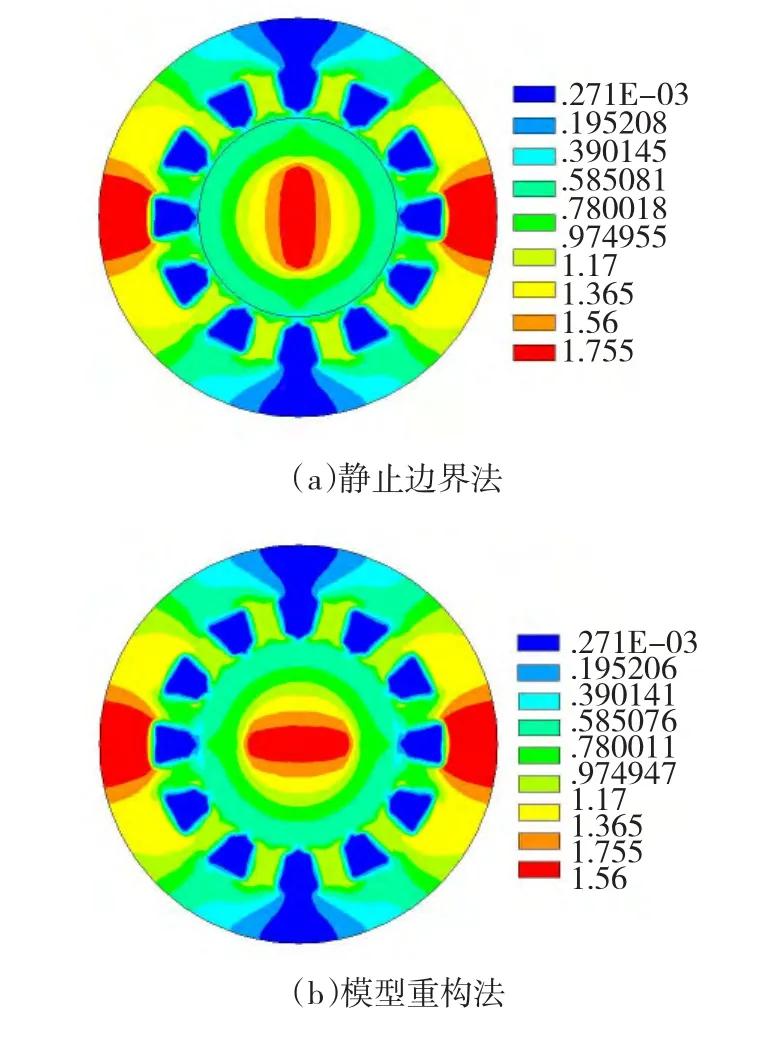
图5 两种方法的磁密分布比较Fig.5 Comparison of two methods on magnetic flux density distribution

2.4 静止边界法与模型重构法计算效率比较

选择ANSYS软件，并采用参数化程序实现图1所示的两种计算流程，对两种方法针对转子旋转一周的计算时间进行比较，见表2。可以看出静止边界法由于不需要重复建模、划分网格，其计算效率要明显高于模型重构法。这里还需要说明的是步长的选择会影响到模型的单元精度、求解自由度的数量以及单次求解的时长，因此不同步长与计算时长之间并不存在绝对的线性关系。

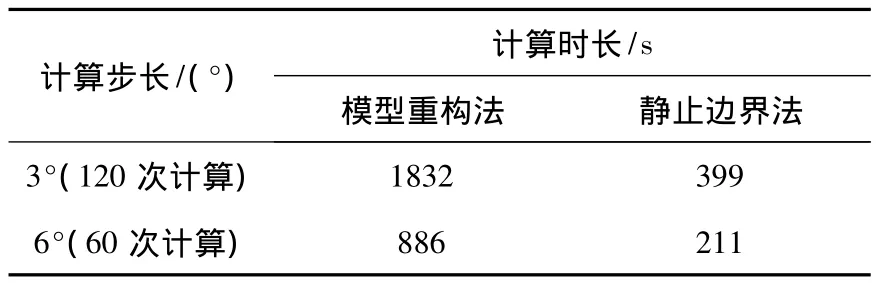
表2 计算时间比较Table 2 Comparison of computation time

3 静止边界法在电机铁耗计算中的应用

电机定子损耗计算的核心是铁耗模型的选择，但是无论采用哪种铁耗模型都必须基于定子铁心中任一单元的时域磁密波形。静止边界法的引入为任一单元时域磁密波形的计算提供了可能。如图6所示，在模拟转子不同位置的过程中，由于转子的旋转只是通过节点耦合顺序实现，所以定、转子中单元的形状、编号、所对应的节点信息都不发生变化。

为了说明铁耗计算的方法，分别选择如图6所示的E1、E2、E3、E4四个单元，图7为空载状态下转子处于不同位置时，四个单元对应的径向磁密波形及谐波分析图。图8为四个单元对应的周向磁密波形及谐波分析图。针对本文所提的验证模型，尽管磁密最大值出现在定子的轭部，但是其谐波含量相对较少;而定子的齿部磁密波形近似方波，其谐波量值较大。

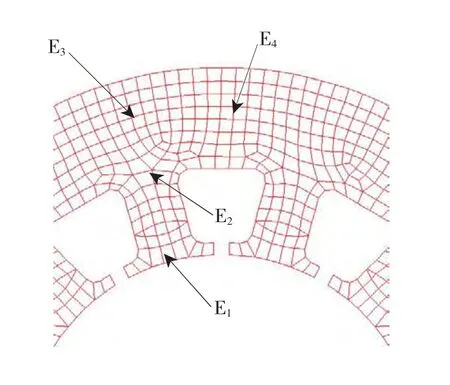
图6 有限元模型Fig.6 Finite element model

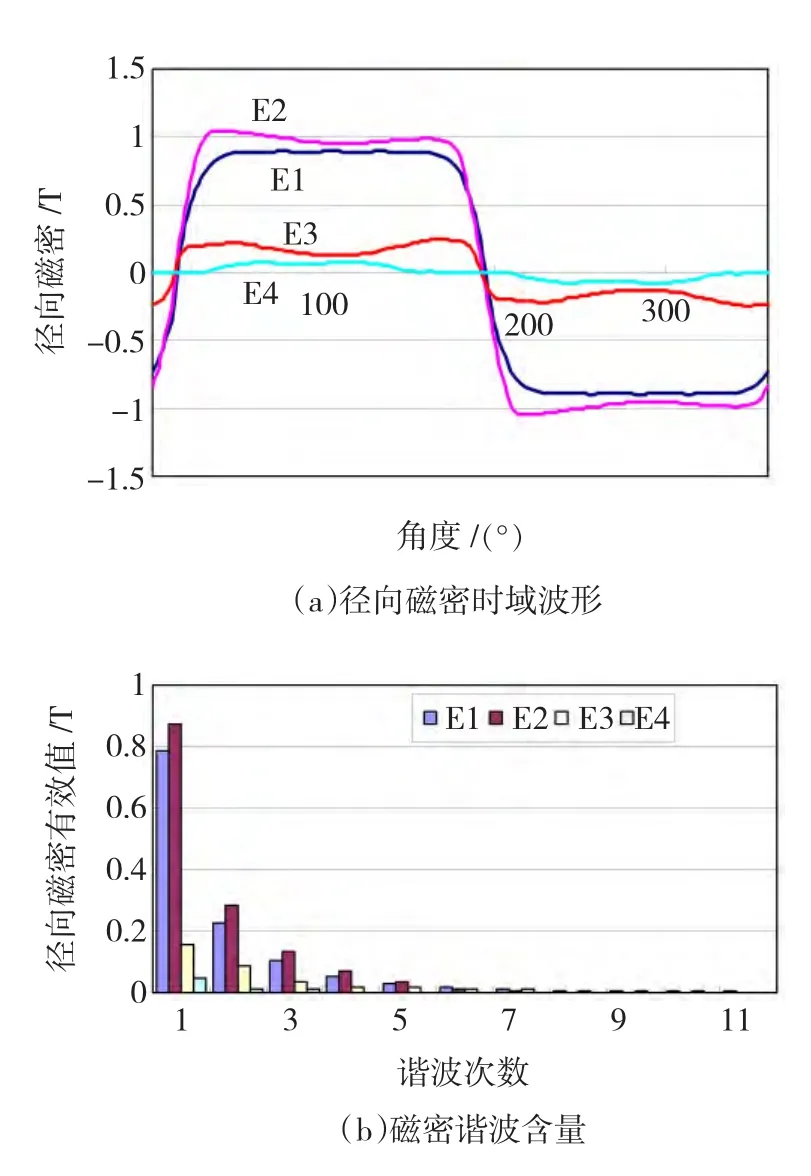
图7 径向磁密Fig.7 The radial magnetic flux density

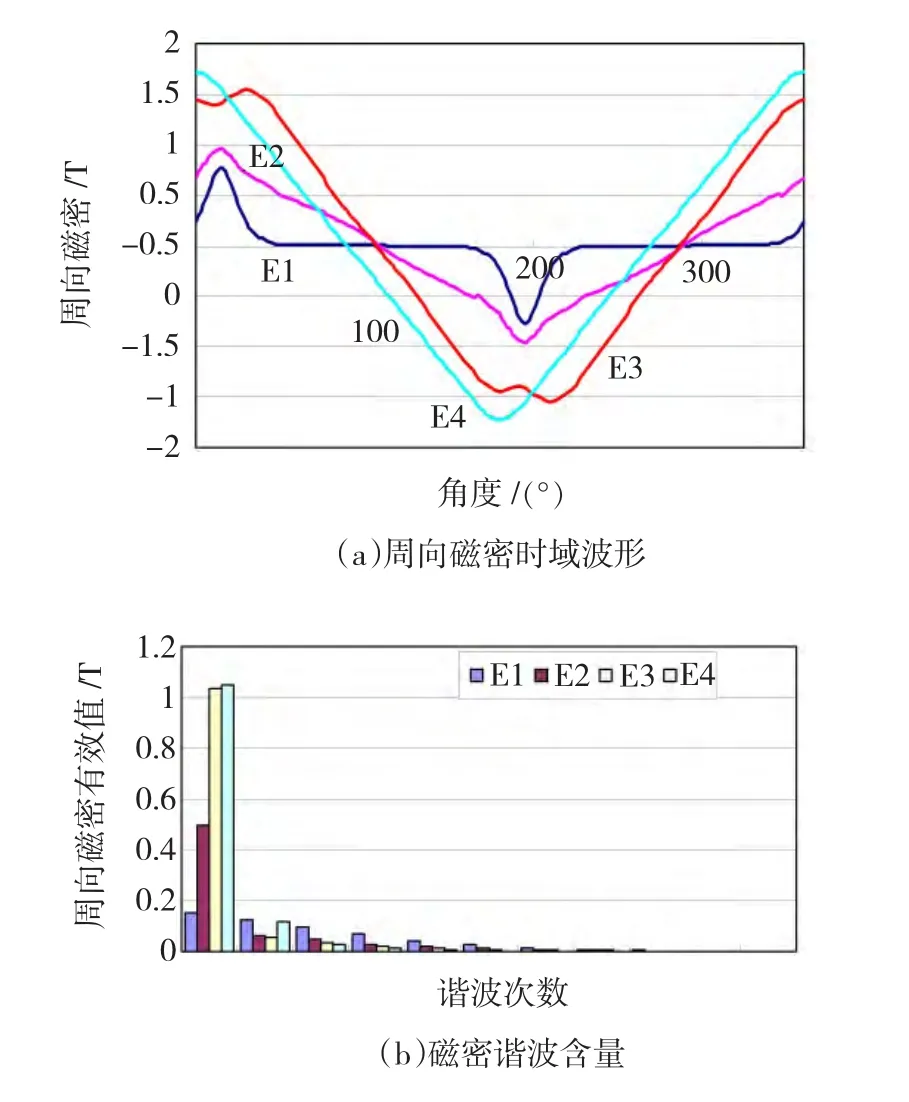
图8 周向磁密Fig.8 The circumferential magnetic flux density

根据谐波分析原理，电机中任意单元的磁通密度波形都可以分解成一系列的谐波分量，任意磁场波形下产生的铁耗等于其基波和各次谐波分量产生的铁耗之和［12－14］。因此各损耗组分的计算公式如下:

a)涡流损耗:

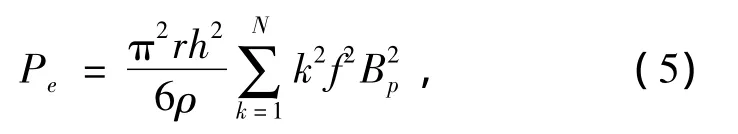
式中:r为铁心电导率;h为铁心厚度;k为谐波次数;f为基波频率;BP为第k次谐波对应的磁密幅值;ρ为铁心密度。

b)磁滞损耗:

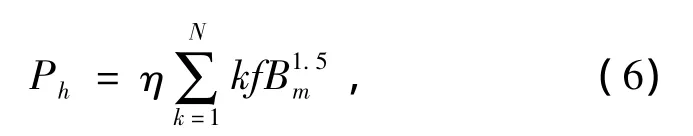
式中:Bm为单元磁密的最大值;η为磁滞损耗系数，η是进行铁耗计算的关键参数，通过文献［15］中的方法求取。

利用静止边界有限元法进行磁场分析，可以得到定子铁心中各个单元磁通密度矢量随转子位置变化的波形，对其进行傅立叶分解，求得磁密的基波及各次谐波;根据式(2)、(3)求得铁心中的各损耗组成。在此基础上总损耗可进一步由下式求得:

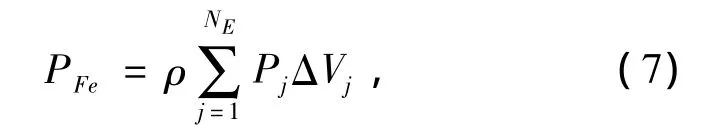
式中:NE为单元总数;Pj为各单元的单位质量铁心损耗;ΔVj为各单元面积。

图9为定子铁心中损耗分布(单位W/kg)。可以看出定子损耗主要集中在定子齿部，这与图5得到磁密最大的区域并不一致，这是因为在齿部区域的磁密谐波含量较高，从而导致了过高的损耗密度。

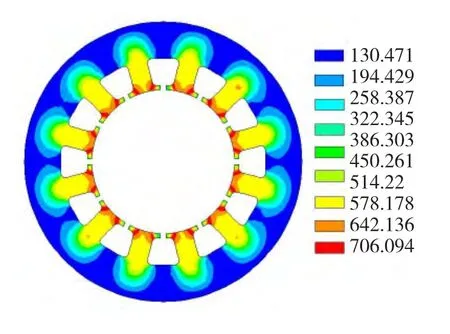
图9 定子铁心损耗分布Fig.9 Core loss distribution

电机铁耗的准确计算一方面取决于电机旋转磁场分布的准确计算，另一方面就是基于材料特性的铁耗模型。这里要说明的是本文研究的重点并不是铁耗模型的建立及选择，而是在于静止边界条件在铁耗计算中的应用，以及该方法对铁耗分布准确计算的意义。

4 结论

本文提出一种高效计算永磁同步发电机旋转磁场分布的静止边界法，该方法通过改变边界节点磁位的耦合顺序来等效转子旋转的位置，克服了模型重构法电磁计算过程中需反复建立模型所导致的效率底下问题。通过比较两种方法的计算结果，验证了静止边界法在电机旋转磁场计算时的正确性和高效性。同时静止边界法保证了在转子旋转一周的整个计算过程中，定、转子模型中有限元单元的形状、位置及构成节点信息的一致性，为永磁同步发电机定子铁耗分布的准确计算提供了可能。

［1］刘瑞芳，严登俊，胡敏强.永磁无刷直流电动机场路耦合运动时步有限元分析［J］.中国电机工程学报，2007，27(12):59－64.LIU Ruifang，YAN Dengjun，HU Minqiang.Field circuit and movement coupled time stepping finite element analysis on permanent magnet brushless DC motors［J］.Proceedings of the CSEE，2007，27(12):59－64.

［2］谢德馨，阎秀恪，张奕黄，等.旋转电机绕组磁链的三维有限元分析［J］.中国电机工程学报，2006，26(21):143－148.XIE Dexin，YAN Xiuke，ZHANG Yihuang，et al.Three dimensional finite element analysis of winding magnetic flux linkage in rotary electric machines［J］.Proceedings of the CSEE，2006，26(21):143－148.

［3］王爱龙，熊光煜.无刷双馈电机时步有限元分析［J］.中国电机工程学报，2008，28(21):123 －127.WANG Ailong，XIONG Guangyu.Analysis of brushless doublyfed machine by time stepping finite element method［J］.Proceedings of the CSEE，2008，28(21):123－127.

［4］孙玉坤，吴建兵，项倩雯.基于有限元法的磁悬浮开关磁阻电机数学模型［J］.中国电机工程学报，2007，27(12):33－40.SUN Yukun，WU Jianbing，XIANG Qianwen.The mathematic model of bearingless switched reluctance motor based on the finiteelement analysis［J］.Proceedings of the CSEE，2007，27(12):33－40.

［5］黄允凯，胡虔生，朱建国.顾及旋转铁耗的高速爪极电机三维磁热耦合分析［J］.电工技术学报，2010，25(5):54－60.HUANG Yunkai，HU Qiansheng，ZHU Jianguo.Magneto-thermal analysis of a high-speed claw pole motor considering rotational core loss［J］.Transactions of China Electrotechnical Sosiety，2010，25(5):54－60.

［6］沈建新，李鹏，郝鹤，等.高速永磁无刷电机电磁损耗的研究概况(英文)［J］.中国电机工程学报，2013，33(3):62－74，14.SHEN Jianxin，LI Peng，HAO He，et al.Study on electromagnetic losses in high-speed permanent magnet brushless machinesthe state of the art［J］.Proceedings of the CSEE，2013，33(3):62－74，14.

［7］韩力，王华，马南平，等.无刷双馈电机谐波铜耗与铁耗的分析与计算［J］.电机与控制学报，2012，16(3):22－29.HAN Li，WANG Hua，MA Nanping，et al.Calculation and analysis of harmonic copper losses and iron losses of brushless doublyfed machine［J］.Electric Machines and Control，2012，16(3):22－29.

［8］孔晓光，王凤翔，徐云龙，等.高速永磁电机铁耗的分析和计算［J］.电机与控制学报，2010，14(9):26 －30.KONG Xiaoguang，WANG Fengxiang，XU Yunlong，et al.Analysis and calculation of iron losses of high-speed permanent magnet machines［J］.Electric Machines and Control，2010，14(9):26－30.

［9］罗富强，夏长亮，乔照威，等.PWM激励下异步电机铁耗等值电阻模型［J］.电工技术学报，2012，27(7):101 －108.LUO Fuqiang，XIA Changliang，QIAO Zhaowei，et al.Model of equivalent iron loss resistance of induction motor fed by PWM［J］.Transactions of China Electrotechnical Sosiety，2012，27(7):101－108.

［10］严登俊，刘瑞芳，胡敏强，等.处理电磁场有限元运动问题的新方法［J］.中国电机工程学报，2003，23(8):164 －168.Yan Dengjun，LIU Ruifang，HU Minqiang，et al.A new method to deal with the motion problem in electromagnetic field finite element analysis［J］.Proceedings of the CSEE，2003，23(8):164－168.

［11］章跃进，张东.旋转电机磁场计算中转子的自由转动［J］.电工技术学报，2006，21(8):1 －4，30.ZHANG Yuejin，ZHANG Dong.Rotor free movement in magnetic field computation of electric machines［J］.Transactions of China Electrotechnical Sosiety，2006，21(8):1－4，30.

［12］郭健，林鹤云，徐子宏，等.变压器阶梯接缝铁心的损耗计算［J］.东南大学学报:自然科学版，2007，37(1):60 －63.GUO Jian，LIN Heyun，XU Zihong，et al.Co mputation of losses in step-lap lam inated transformer cores［J］.Journal of Southeast University:Natural Science Edition，2007，37(1):60－63.

［13］张艳丽，孙小光，白保东，等.晶粒无取向硅钢片取向特性分析［J］.电工技术学报，2013，28(2增):99－104.ZHANG Yanli，SUN Xiaoguang，BAI Baodong，et al.Analysis on oriented characteristics for non-grain oriented silicon steel sheet［J］.Transactions of China Electrotechnical Sosiety，2013，28(2):99－104.

［14］TENYENHUIS E G.Other factors contributing to the core loss performance of power and distribution transformers［J］.IEEE Transactions on Power Delivery，2001，16(4):648－653.

［15］MECHLER G F.Calculation of spatial loss distribution in stacked power and distribution transformer cores［J］.IEEE Transactions on Power Delivery，1998，13(2):532－537.