永磁同步电机用坐标变换的电流谐波抑制方法
刘刚, 孙庆文, 肖烨然
(1.北京航空航天大学 惯性技术重点实验室,北京100191;2.北京航空航天大学新型惯性仪表与导航系统技术国防重点学科实验室,北京100191)
0 引言
永磁同步电机具有功率密度大、几何尺寸小、效率高、响应快等优点,随着钕铁硼等永磁材料性能的日益提高以及控制理论、高性能处理器和大功率高开关速度功率电子元器件的发展,永磁同步电机应用越来越广泛,如微型涡轮发电机、分子泵、离心压缩机等。由于气隙磁场的畸变以及逆变器非线性等原因,永磁同步电机电流中含有大量的高次谐波,电流波形发生畸变。谐波电流会增加电机的铁耗和铜耗,使电机发热,同时还会增加噪声,引起转矩脉动[1-2]。因此,谐波电流的抑制是改善电机性能,降低功耗的关键技术。
针对谐波电流产生的原因,谐波电流抑制方法的研究主要集中在两个方面。第一种是从电机设计的角度出发,优化电机设计,提高电机反电势的正弦度,降低电机本体的非理想特性[3-4]。第二种是从控制算法的角度,对逆变器固有的管压降和死区时间等非线性因素所产生的谐波电流进行补偿[5-8]。文献[5]通过前馈补偿,可以抑制逆变器死区时间所引起的5次和7次谐波电流,但对其他原因产生的谐波电流抑制作用不明显。文献[6]提出了时间补偿法,根据误差电压与电机相电流极性的关系,对逆变器驱动信号进行补偿,抑制死区效应造成的影响。但由于零电流箝位现象的影响,电机相电流极性难以准确判断,容易给出错误的补偿量,影响控制效果。文献[7]提出一种傅里叶变换和重复控制相结合的方法,可对多个谐波产生抑制作用,但实际中控制效果较好并且稳定的重复控制器参数设定比较复杂。由于常规PI控制器无法对周期性误差做到无误差跟踪,文献[8]采用比例积分加比例谐振的电流复合调节器,虽然减小了谐波电流,但容易造成不同频率谐波之间的相互干扰,影响系统的稳定性。此外还有其他一些方法应用到电流谐波抑制中[9-10],但由于控制系统及硬件电路存在延时,过于复杂的算法在实际中并不能取得理想的效果。
针对以上方法的不足,本文在分析永磁同步电机谐波产生原因的基础上,提出一种基于同步旋转坐标变换的指定次谐波补偿法,通过谐波电流环的引入,对不同原因造成的5次和7次谐波电流进行归一化的补偿。这种方法计算简单,不需要增加任何硬件电路和离线测试,通过仿真分析和实验证明了该方法的有效性和实用性。
1 永磁同步电机电流谐波分析
根据永磁同步电机谐波的性质,可以将运行谐波分为两类:时间谐波和空间谐波。时间谐波主要是逆变器本身的非线性特性所引起的,实际运行中的电力电子器件并不是理想开关,存在死区时间和管压降等非线性因素。死区时间和管压降的存在会导致逆变器输出电压波形发生畸变,从而产生高次谐波电流。空间谐波主要是电机本体在运行过程中产生的,由于空间谐波的存在,即使通入三相绕组的电流为标准正弦波,气隙磁场也会发生畸变。影响电机空间谐波的主要因素有:齿槽效应、绕组分布形式、磁路磁饱和程度、转子磁极结构等[11]。时间谐波的特点是时间相关,谐波函数以时间为变量;而空间谐波的特点是与位置相关的,谐波函数以转子位置为变量。
在同步旋转dq坐标系下表贴式永磁同步电机电压方程为:

式中:ud、uq分别为dq轴电压;id、iq分别为dq轴电流;Ld、Lq分别为dq轴电感;Rs为定子电阻;ψf为转子永磁体磁链;ωr为基波电压的角速度。
在电机稳定运行状态下,若只含有基波,则dq轴电流和电压均为直流量。在实际系统中,由于谐波分量的存在,ud、uq不再是直流量,含有由谐波变换到dq轴系下的一系列交流分量,影响电机的控制性能。
永磁同步电机属于对称的三相三线系统,在定子绕组的谐波电流中,偶次谐波不存在。并且对称系统中n次的谐波电流三相互差2nπ/3,即具有如下关系:

式中:ian、ibn、icn分别为 a、b、c 三相的 n 次谐波电流;Im为谐波电流幅值;φn为谐波电流的初始相位角。由上式可以看出,不同次的谐波电流在电路中存在不同规律。
当 n=3k(k=1,2,3…)时,三相电流中的 n 次谐波电流不仅相位相同,而且幅值相等,永磁同步电机定子绕组是星型连接,使得3k次的谐波电流没有导通回路,在绕组中不存在。
当 n=3k+1(k=1,2,3…)时,a相电流滞后 c相电流2π/3,a相电流超前b相电流2π/3,同基波电流呈现出相同的规律,可认为是正序谐波电流。
当 n=3k-1(k=1,2,3…)时,a相电流滞后 b相电流2π/3,a相电流超前c相电流2π/3,可认为是负序谐波电流。
所以,永磁同步电机定子绕组中主要含有5次和7次等高次谐波电流,其中5次谐波为负序谐波电流,7次谐波为正序谐波电流,电机内的电流可以表示成如下形式:
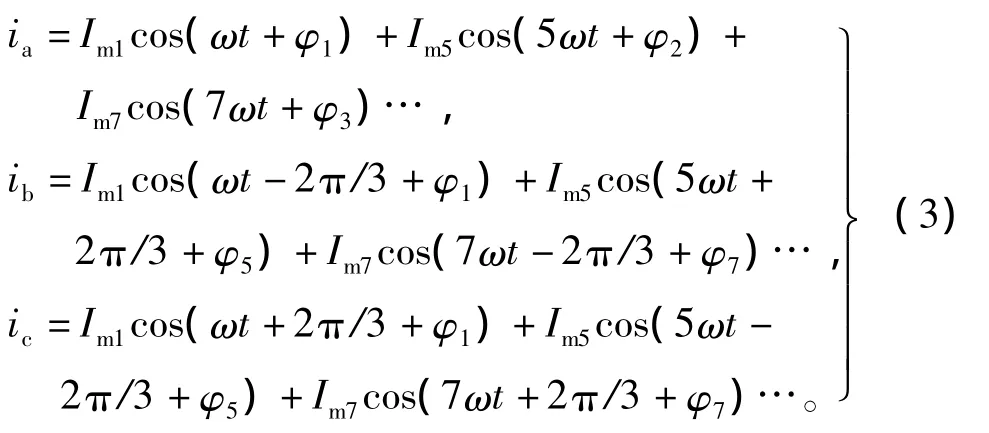
2 谐波抑制算法
传统的PI控制器在理论上可以做到对直流恒定信号的无静差跟踪,并且具有稳态精确度高、动态响应好、工程性应用简单实用的特点,但PI控制器不能对周期性信号做到无静差跟踪。所以将检测到的负载电流信号通过与某指定次谐波角速度同步的旋转坐标变换转化成直流量,通过低通滤波器将直流量提取出来,对此直流量进行电流PI控制,理论上可以做到对指定次谐波的无静差跟踪。并行的增加5次和7次谐波电流控制环,可以将其叠加组成完整的谐波电流控制器,从而能够对5次和7次谐波产生控制作用,达到抑制谐波电流的目的。
所提出的基于多同步旋转坐标变换的谐波抑制算法整体控制结构图如图1所示。
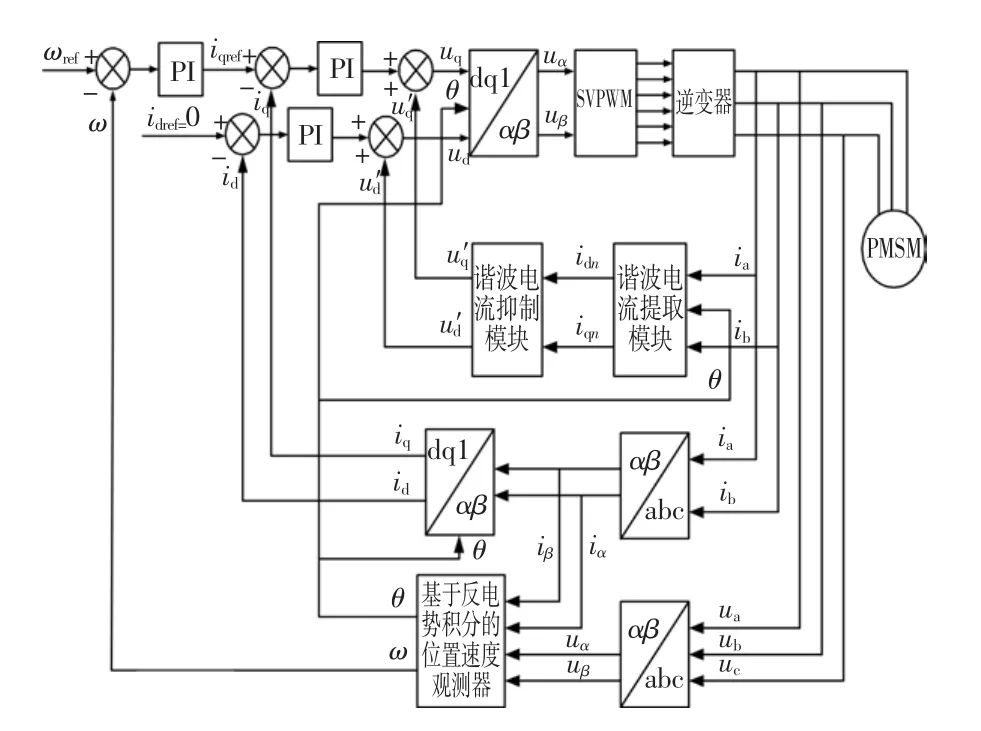
图1 加入谐波抑制算法的矢量控制系统框图Fig.1 The schematic of vector control with harmonic suppression method
电机控制方式选用idref=0的矢量控制策略,转子位置和速度信息通过基于反电势积分的位置速度估测器得到[12-13]。对表贴式永磁同步电机,在静止αβ坐标系下的数学模型可简化为
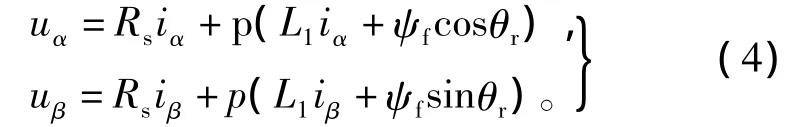
式中:uα、uβ、iα、iβ分别为 αβ 轴上的等效电压和等效电流;p=为微分算子;L=;θ为转子角1r位置。定子磁链ψα和ψβ由积分得到
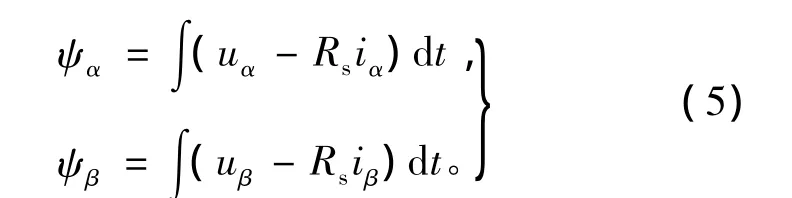
则估算的转子角位置和角速度为
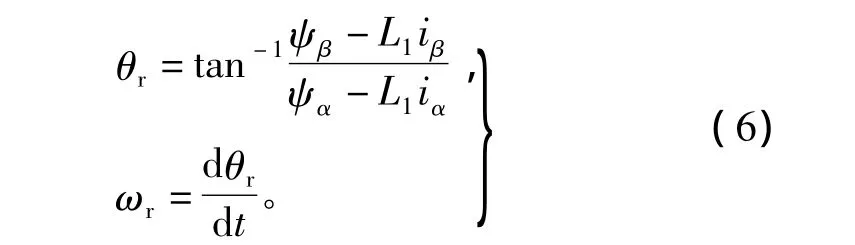
在矢量控制系统原有的转速电流双闭环控制系统的基础上增加了谐波电流控制环,对影响系统性能的5次和7次谐波电流进行抑制。增加的谐波电流控制环主要由谐波电流提取模块和谐波电流抑制模块两部分组成。
2.1 谐波检测
在dq坐标变换的基础上,采用同步旋转dq坐标变换检测法,将5次和7次谐波转变为直流量。根据同步旋转坐标变换的原理,如果某一频率分量和dq同步旋转轴系的速度相等并且方向一致,则该频率分量在此dq轴系下为直流分量。因此在5次谐波对应的dq同步旋转坐标轴系下,5次谐波分量变换为直流分量,基波以及其他各次谐波分量是交流分量。在7次谐波对应的dq同步旋转坐标轴系下,7次谐波分量变换为直流分量,基波以及其他各次谐波分量是交流分量。根据以上原理设计谐波提取模块,如图2所示,电机相电流ia、ib分别进行5次谐波坐标变换和7次谐波坐标变换,将坐标变换完成后的信号经过低通滤波器,即可得到5次和7次谐波在相应的同步dq旋转坐标系中所对应的直流量 id5,iq5,id7,iq7。
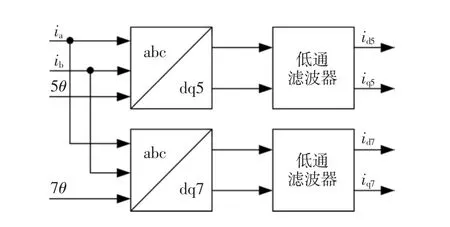
图2 谐波电流提取模块Fig.2 Extraction modules of harmonic currents
在有源电力滤波器谐波抑制方法的研究中,文献[14]详细分析了对任意指定次谐波进行提取的方法。5次谐波的旋转方向与基波相反,为负序数谐波,由abc静止坐标系到5次谐波dq同步旋转坐标系的坐标变换分两部分完成,首先是通过CLARK变换从abc静止坐标系变换到两相静止αβ坐标系,然后利用PARK变换的原理从两相静止αβ坐标系变换到5次谐波dq同步旋转坐标系,与传统PARK变换不同的是此时旋转角速度不同,5次谐波坐标系的旋转速度为-5ωt,具体公式如下所示
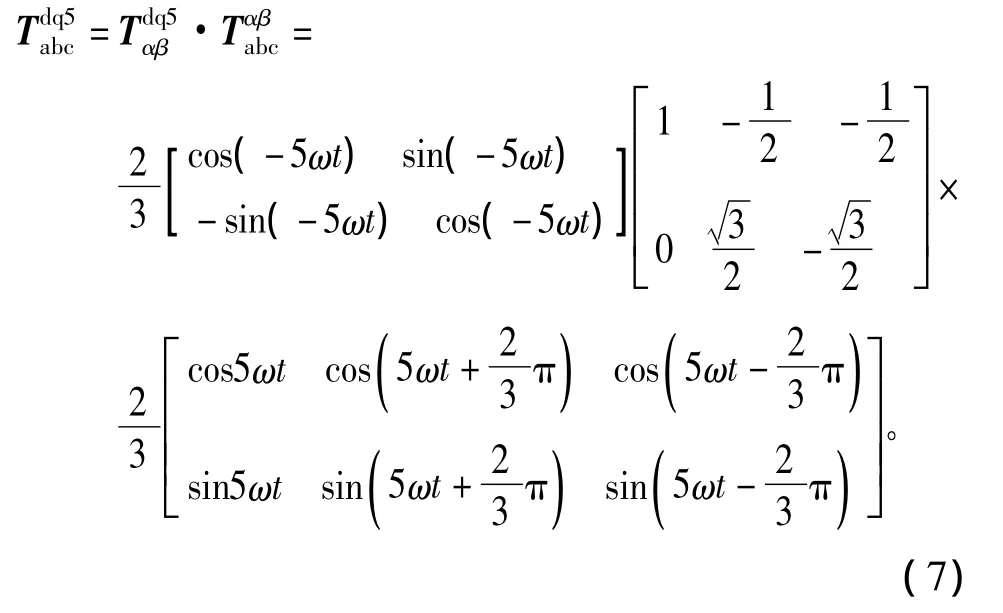
7次谐波的旋转方向与基波相同,为正序数谐波,由abc静止坐标系到7次谐波dq同步旋转坐标系的变换与5次谐波的变换类似也由两部分组成,具体变换如下所示。
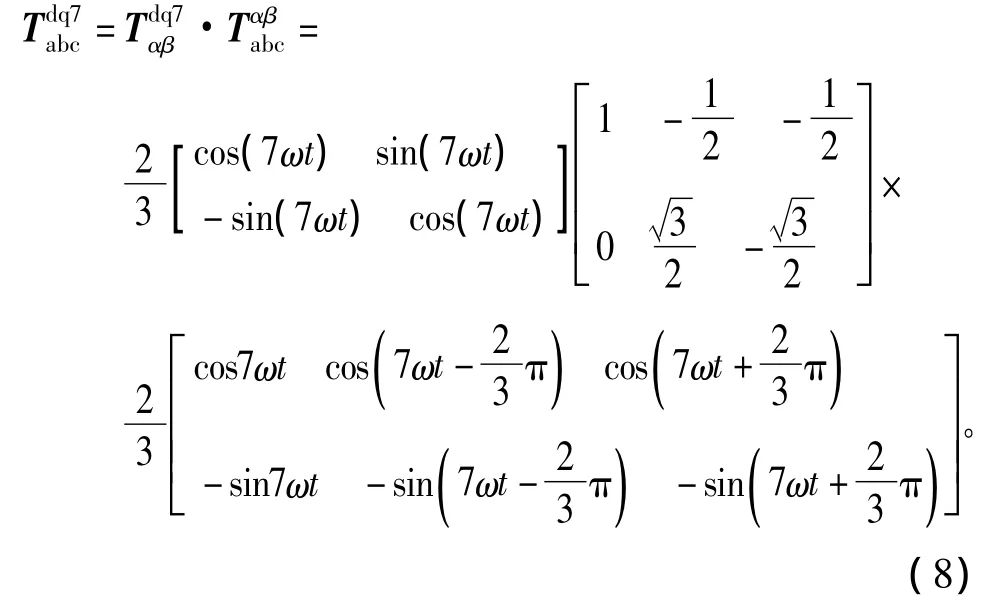
2.2 谐波抑制
通过谐波检测模块,分别检测出5次和7次谐波电流在相应谐波坐标系中所对应的直流量。将此直流量送入各自的PI控制器,即可产生抑制5次和7次谐波的控制量。由于谐波电流控制是在基波dq旋转坐标系中实现的,所以需要将谐波旋转坐标系中PI控制器产生的控制量转换到基波旋转坐标系下,然后作为前馈控制量加入到电流环中。
5次谐波到基波的旋转坐标变换为

7次谐波到基波的旋转坐标变换为:
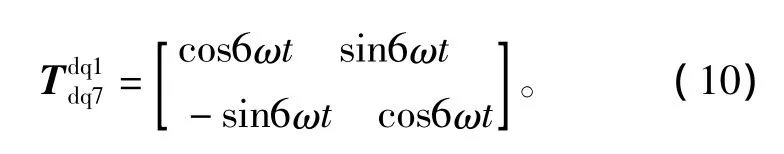
整体结构如图3所示。

图3 谐波电流抑制模块Fig.3 Suppression modules of harmonic currents
图中,id5ref,iq5ref,id7ref,iq7ref为给定的控制目标量均为零;ud5,uq5,ud7,uq7为5 次和 7 次谐波分别在基波dq旋转坐标系中的控制量;u'd,u'q为最终加到电流环的前馈补偿量。
3 仿真分析
选取纯电磁磁轴承表贴式永磁同步电机来验证谐波抑制算法的可行性,搭建Matlab/SIMULINK仿真模型并进行仿真研究。具体参数在20℃时为:相电阻Rs=40 mΩ,交、直轴电感Ld=Lq=0.17 mH,反电动势系数ke=4.15 V/(kr/min),极对数P=1。控制系统整体结构如图1所示。
在实际的系统中,电机制造工艺、逆变器非线性特性和电感饱和等都会造成电流波形的畸变。在采用无位置传感器控制方式时,观测器观测的速度和位置信息可能与转子真实的速度和位置有一定误差,这也会造成电流波形畸变,谐波含量增高。为了简化模型的需要,在仿真模型中通过设置3 V的逆变器管压降和10 μs的死区时间来产生谐波电流。通过对加入谐波抑制算法前后电机电流波形的分析来验证算法的有效性。
图4为传统矢量控制方式下电机在9000r/min时的电流仿真图形。从图中可以看出,由于谐波源的存在,电机电流不再是标准的正弦波,谐波含量比较高以致波形发生严重畸变。快速傅里叶变换的结果表明5次谐波和7次谐波是谐波源的主要成分,其含量分别高达15.77%和6.78%。
图5为加入谐波抑制算法后,电机在9000r/min时的电流波形图。从仿真结果来看,与加入算法前相比,电流的正弦度明显提升。快速傅里叶变换的结果表明,谐波分量明显减少,5次谐波和7次谐波得到较好的抑制,其含量分别减少到2.21%和1.48%。从加入谐波抑制算法前后仿真结果的对比可以得知,该方法可以有效地抑制造成电机电流波形畸变的5次谐波和7次谐波,证明了该算法的可行性。

图4 9000r/min时未加入补偿的仿真结果Fig.4 Result of simulation without compensation when n=9000r/min
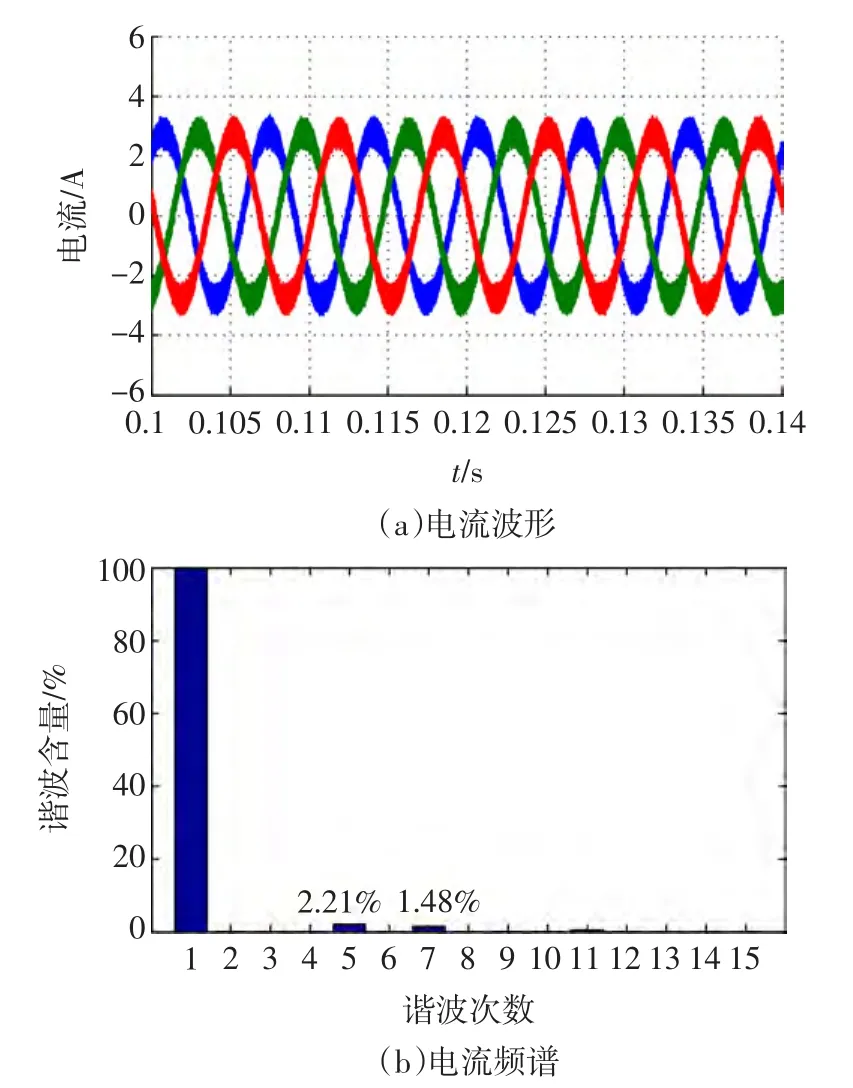
图5 9000r/min时加入补偿后的仿真结果Fig.5 Result of simulation with compensation when n=9000r/min
4 实验结果分析
为了验证所提方法的实用性,选用电机参数与仿真参数相同的磁悬浮永磁同步电机进行实验,搭建电机控制系统实验平台。电机控制方式选用id=0的矢量控制策略,控制系统以 TI公司的TMS320F28335型DSP为核心,功放模块采用三菱IPM(PM25RLA120),设定其开关频率为10 kHz,死区时间设定为 10 μs。id和 iq通过外接的 DA(TLV5614)芯片输出到示波器。图6为电机与控制系统实物图。

图6 系统实物图Fig.6 Photo of the system
图7 为未加入谐波抑制算法时,电机稳定运行在9000r/min的A相电流波形。从实验结果可以看出,此时电流波形失真严重,谐波含量很高。通过快速傅里叶变换进行谐波分析可以发现,造成电流发生畸变的主要谐波仍然是5次谐波和7次谐波,与理论分析和仿真实验的结果相符合。

图7 9000r/min时未加入补偿的实验结果Fig.7 Result of experimentation without compensation when n=9000r/min
图8为加入传统前馈补偿算法后,在9000r/min时A相电流波形。通过快速傅里叶变换进行谐波分析可以得知,5次谐波含量为8.35%,7次谐波含量为2.92%,谐波含量仍然较大。
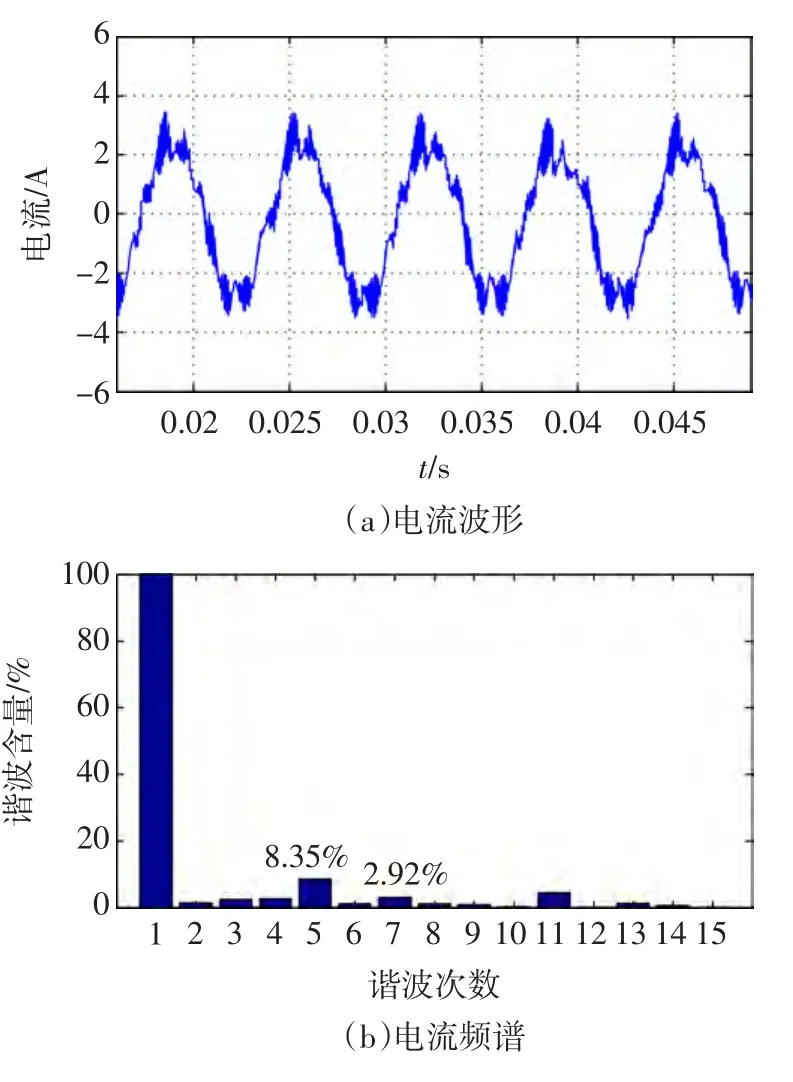
图8 9000r/min时加入传统前馈补偿后的实验结果Fig.8 Result of experimentation with traditional feedforward compensation when n=9000r/min
图9 为加入谐波抑制算法后,电机稳定运行在9000r/min时的A相电流波形。从实验结果来看,由于该算法的引入,电流波形发生明显改变,正弦度提高。通过快速傅里叶变换进行谐波分析可以得知,谐波分量得到很好的抑制,5次谐波含量下降到2.36%,7次谐波含量下降到1.17%,证明了该方法在实际系统中的可行性。
通过坐标变换的知识可以得知,静止abc坐标系下的5次谐波和7次谐波通过CLARK变换和PARK变换,会转变为d轴和q轴的电流中的6次谐波。d轴和q轴的电流无法用电流钳直接测得,通过外接的DA(TLV5614)芯片,将id和iq输出到示波器进行观察。图10为不同实验条件下,得到的d轴和q轴电流波形图,其中绿色的曲线代表id,蓝色的曲线代表iq。
对于表贴式永磁同步电机,当采用id=0的矢量控制时,电磁转矩可以表示为


图9 9000r/min时加入本文方法的实验结果Fig.9 Result of experimentation with the proposed method when n=9000r/min
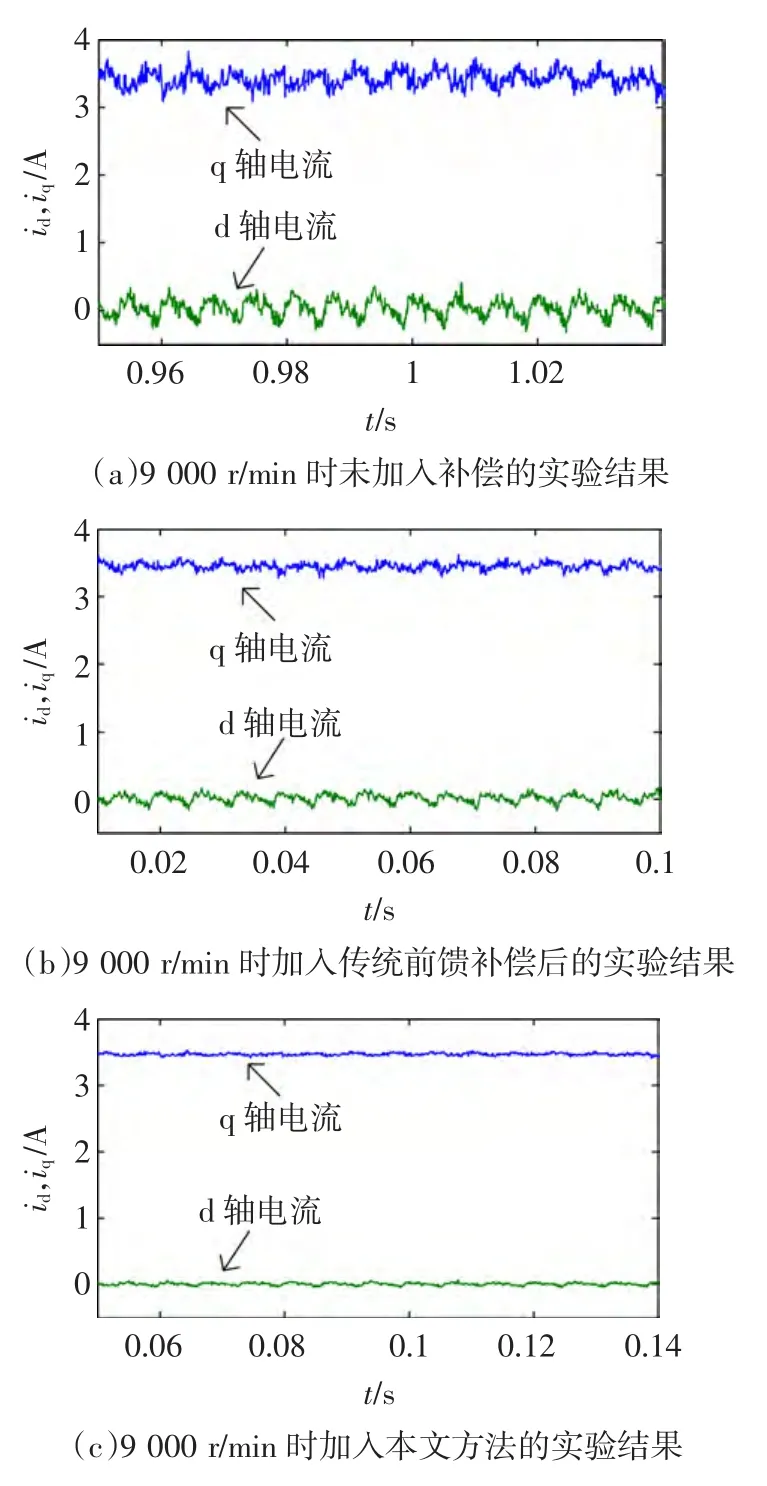
图10 不同实验条件下id和iq电流波形图Fig.10 Current waveform of idand iqunder different experimental conditions
电磁转矩Te与iq成线性关系,iq的波动是造成电磁转矩脉动的直接原因,通过图10可以发现,加入了谐波抑制算法后,id和iq的波动得到了有效地抑制,从而可以削弱转矩脉动,提高电机运行的平稳性。
5 结论
本文针对永磁同步电机运行过程中电流谐波含量高的问题,提出了基于同步旋转坐标变换的谐波抑制方法。在原有的矢量控制双闭环基础上,增加了抑制5次谐波电流和7次谐波电流的谐波电流环。该算法不需要增加任何硬件电路和离线测试,并且计算简单,容易实现。仿真分析和实验结果可以证明,该算法可以有效地抑制造成电机电流发生畸变的5次谐波和7次谐波,提高电机电流的正弦性,从而达到减小转矩脉动、降低功耗、改善电机性能的目的。
[1]甄帅.大功率永磁同步电机运行谐波分析与抑制方法研究[D].重庆:重庆大学,2011.
[2]EHSAN A N,BIN W,NAVID R Z,et al.Input power factor compensation for high-power CSC fed PMSM drive using d-Axis stator current control[J].IEEE Transactions on Industrial Electronics,2012,59(2):752 -761.
[3]王秀和,杨玉波,丁婷婷,等.基于极弧系数选择的实心转子永磁同步电动机齿槽转矩削弱方法研究[J].中国电机工程学报,2005,25(15):146 -149.WANG Xiuhe,YANG Yubo,DING Tingting,et al.The method for reducing cogging torque by suitable selection of POLE-ARC coefficient in solid-rotor PM synchronous motors[J].Proceedings of the CSEE,2005,25(15):146 -149.
[4]HAN S H,THOMAS M J,ZHU Z Q.Analysis of rotor core eddycurrent losses in interior permanent magnet synchronous machines[J].IEEE Transactions on Industry Applications,2010,46(1):196-205.
[5]HWANG S H,KIM J M.Dead time compensation method for voltage-fed PWM inverter[J].IEEE Transactions on Energy Conversion,2010,25(1):1 -10.
[6]吴茂刚,赵荣祥,汤新舟.正弦和空间矢量PWM逆变器死区效应分析与补偿[J].中国电机工程学报,2006,26(12):101-105.WU Maogang,ZHAO Rongxia,TANG Xinzhou.Dead-time effects analysis and compensation of SPWM and SVPWM inverter[J].Proceedings of the CSEE,2006,26(12):101 -105.
[7]KIM J S,DOKI S J,ISHIDA M.Improvement of IPMSM sensorless control performance by suppression of harmonics on the vector control using fourier transform and repetitive control[C]//Industrial Electronic Society,IEEE 2002 28th Annual Conference of the IEEE Industrial Electronics Society,November 5-8,2002,Sevilla,Spain.2002:597-602.
[8]王恩德,黄声华.表贴式永磁同步电机伺服系统电流环设计[J].中国电机工程学报,2012,32(33):82-88.WANG Ende,HUANG Shenghua.Current regulator design for surface permanent magnet synchronous motor servo systems[J].Proceedings of the CSEE,2012,32(33):82 -88.
[9]KIM S Y,LEE W,RHO M S,et al.Effective dead-time compensation using a simple vectorial disturbance estimator in PMSM drives[J].IEEE Transactions on Industrial Electronics,2010,57(5):1609-1614.
[10]XIAO X,CHEN C M.Reduction of torque ripple due to demagnetization in PMSM using current compensation[J].IEEE Transactions on Applied Superconductivity,2010,20(3):1068-1071.
[11]廖勇,甄帅,刘刃,等.用谐波注入抑制永磁同步电机转矩脉动[J].中国电机工程学报,2011,31(21):119-127.LIAO Yong,ZHEN Shuai,LIU Ren,et al.Torque ripple suppression of permanent magnet synchronous motor by the harmonic injection[J].Proceedings of the CSEE,2011,31(21):119-127.
[12]韩邦成,王鹏,陈彦鹏.改进滑模观测器的磁悬浮高速P M S M转子位置预测方法[J].电机与控制学报,2013,17(9):42-47.HAN Bangcheng,WANG Peng,CHEN Yanpeng.Rotor position estimation of magnetic suspension high speed permanent magnet synchronous motor based on modified sliding-mode observer[J].Electric Machines and Control,2013,17(9):42 -47.
[13]王子辉,叶云岳.反电势算法的永磁同步电机无位置传感器自启动过程[J].电机与控制学报,2011,15(10):36-42.WANG Zihui, YE Yunyue. Research on self-startup states process of back-EMF based sensorless vector control of PMSM[J].Electric Machines and Control,2011,15(10):36 -42.
[14]AKAGI H,NABAE A,ATOH S.Control strategy of active power filters using voltage source PWM converters[J].IEEE Transactions on Industry Applications,1986,22(3):460 -481.

